游戏中的随机——“动态平衡概率”算法
前言
众所周知计算机模拟的随机是伪随机,但在结果看来依然和现实中的随机差别不大。
例如掷硬币,连续掷很多很多次之后,总有连续七八十来次同一个面朝上的情况出现,计算机中一般的随机函数也能很好模拟这一点。
但在游戏中,假如有一个50%概率会出现的情况,经常连续七八十来次不出现,这样其实非常影响游戏体验。
那么为了增加这部分游戏体验,我们如何避免上述情况发生,使某个概率能在总体上较为均匀地分布呢?
例如现在有这样的需求:
A. 暴击率总体为20%
B. 要求每十次攻击,至少有一次暴击
C. 要求暴击的总体分布较为均匀
算法预览
经过一段时间的深思熟虑,笔者终于构建了一种名为“动态平衡概率”的算法。
虽然它还有一些局限性,但已经达到了基本可用的状态。
先上代码,为了方便演示图表,这里就用 python 了:
import matplotlib.pyplot as plt
import random# 初始化变量
InitCritPercent = 0.2 # 初始暴击率
dynamicCritPercent = 0.2 # 动态暴击率
currentCritPercent = 0 # 当前暴击概率
deltaCritPercent = 0 # 当前暴击率与初始暴击率的差值(用来表示变化)
attackTotalCount = 0 # 总攻击次数
critTotalCount = 0 # 总暴击次数
noCritStreakCount = 0 # 连续未暴击次数# 给 plot 准备的列表
currentCritPercentList = []
deltaCritPercentList = []
dynamicCritPercentList = []
noCritStreakCountList = []
isCriticalList = []# 获取最佳的 N
def find_optimal_N(p):one_minus_p = 1 - pfor i in range(1, 501):if one_minus_p ** i <= 0.05:return ireturn 500 # 如果未找到合适的 N,则默认返回 500# 测试 10000 次
for i in range(10000):# 核心代码 ↓attackTotalCount += 1isCritical = False# 检查当前攻击数是否大于 0if attackTotalCount > 0:# 计算当前暴击概率currentCritPercent = critTotalCount / attackTotalCount# 计算当前暴击概率与初始暴击率的差值deltaCritPercent = abs(InitCritPercent - currentCritPercent)# 计算动态暴击率dynamicCritPercent = (attackTotalCount * (InitCritPercent - currentCritPercent) + currentCritPercent) * pow(deltaCritPercent, 0.5)# 检查是否连续 N - 1 次未暴击if noCritStreakCount < find_optimal_N(InitCritPercent) - 1:percent = random.random()if percent <= dynamicCritPercent:isCritical = TruenoCritStreakCount = 0else:noCritStreakCount += 1else:isCritical = TruenoCritStreakCount = 0if isCritical:critTotalCount += 1# 核心代码 ↑# 将数据添加到列表中currentCritPercentList.append(currentCritPercent)deltaCritPercentList.append(deltaCritPercent)dynamicCritPercentList.append(dynamicCritPercent)noCritStreakCountList.append(noCritStreakCount)isCriticalList.append(int(isCritical))# 创建多表格
fig, axs = plt.subplots(2)# 每 100 条数据标注一下
for i in range(0, len(currentCritPercentList), 100):axs[0].annotate(f"{currentCritPercentList[i]:.3f}", (i, currentCritPercentList[i]))# 画出暴击概率数据表格
axs[0].plot(currentCritPercentList, label='Current Crit Percent', color='r')
axs[0].plot(deltaCritPercentList, label='Delta Crit Percent', color='g')
axs[0].plot(dynamicCritPercentList, label='Dynamic Crit Percent', color='b')
axs[0].set_xlabel('Total Attacks')
axs[0].set_ylabel('Probability')
axs[0].legend()# 画出连续未暴击次数的表格
axs[1].plot(noCritStreakCountList, label='No-Crit Streak', color='m')
axs[1].plot(isCriticalList, label='Is Critical', color='c')
axs[1].set_xlabel('Total Attacks')
axs[1].set_ylabel('No-Crit Streak / Is Critical')
axs[1].legend()plt.show()
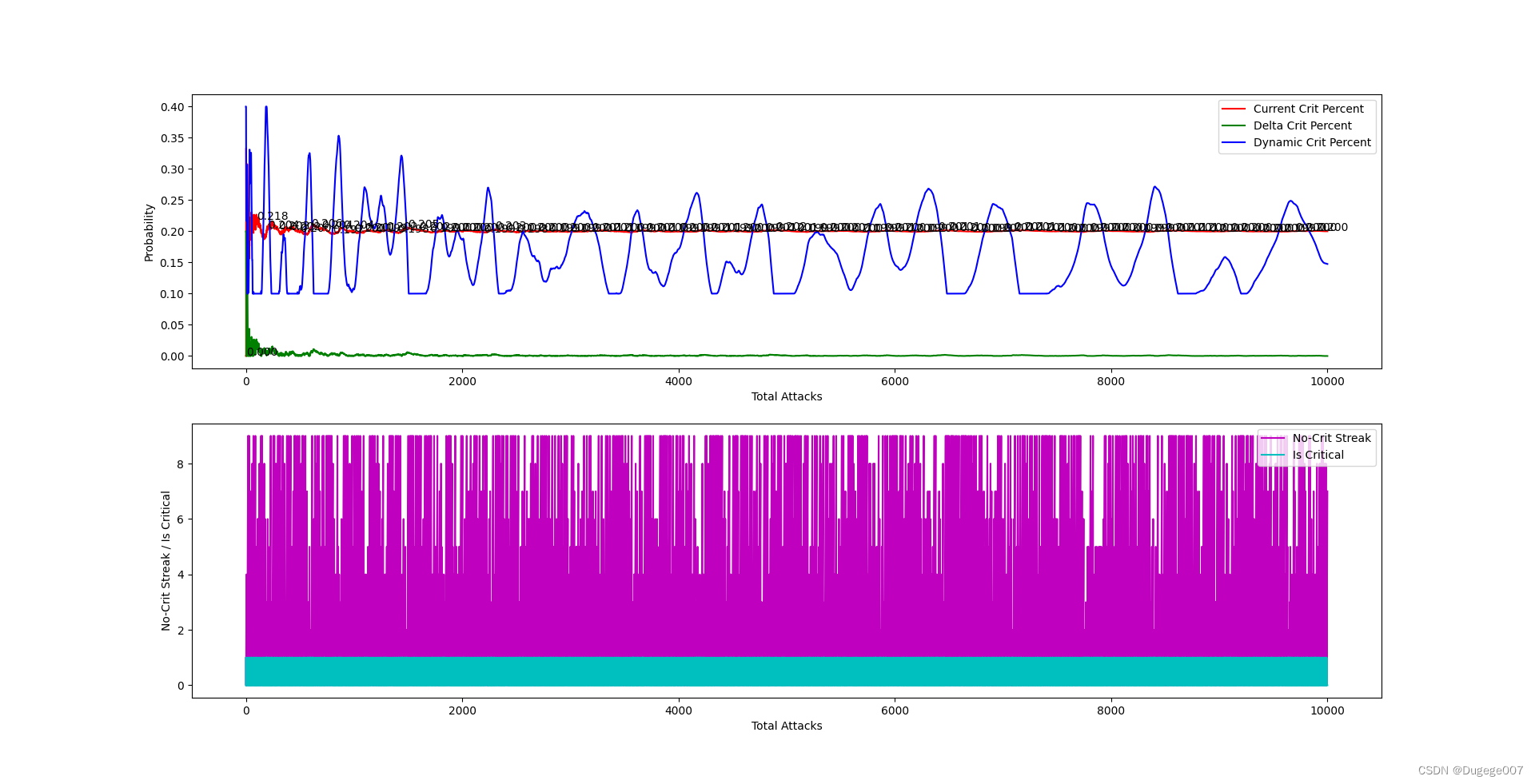
给定参数的运行结果如下图所示(这里的“要求N次攻击,至少有一次暴击”中的N,根据算法取了14)
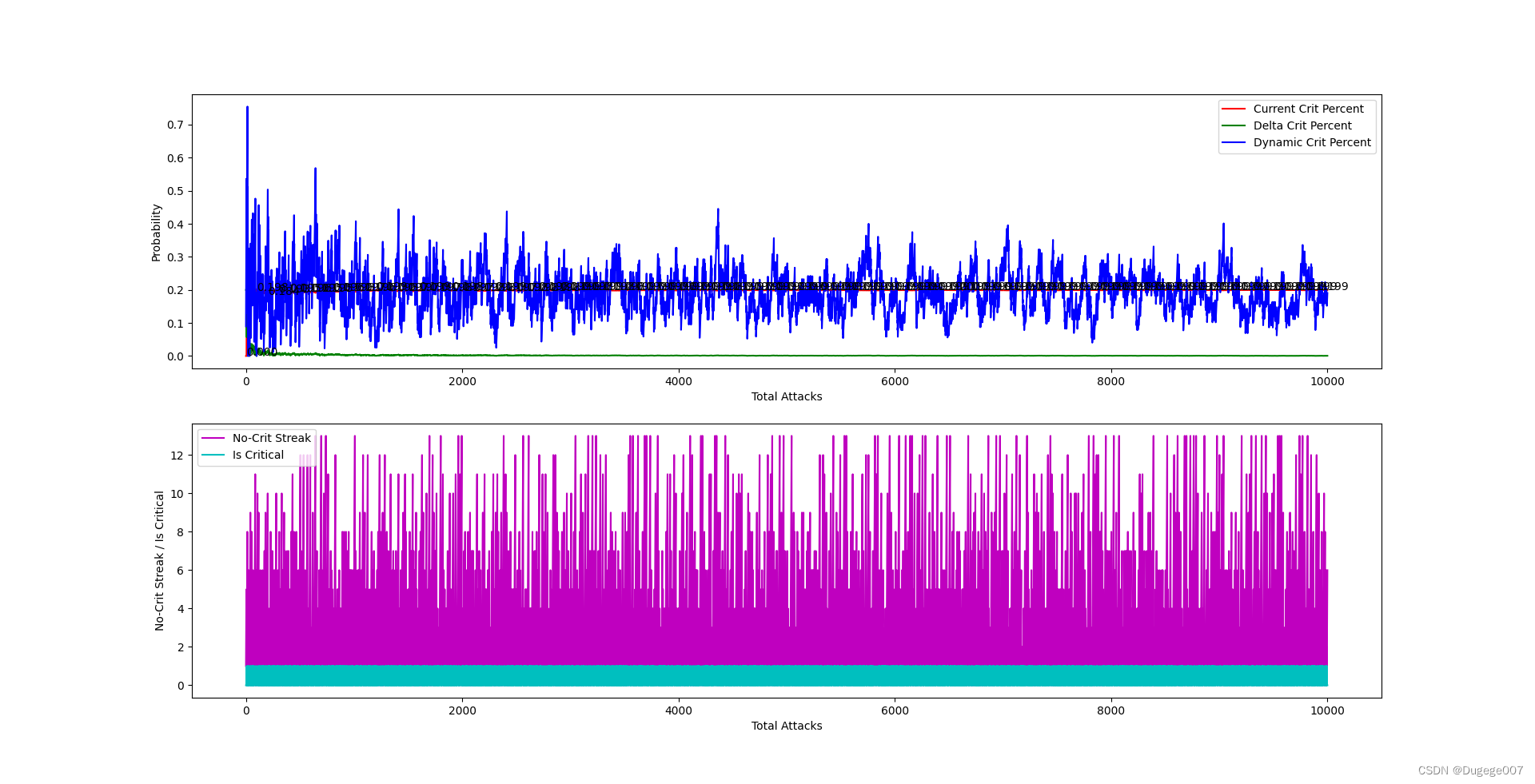
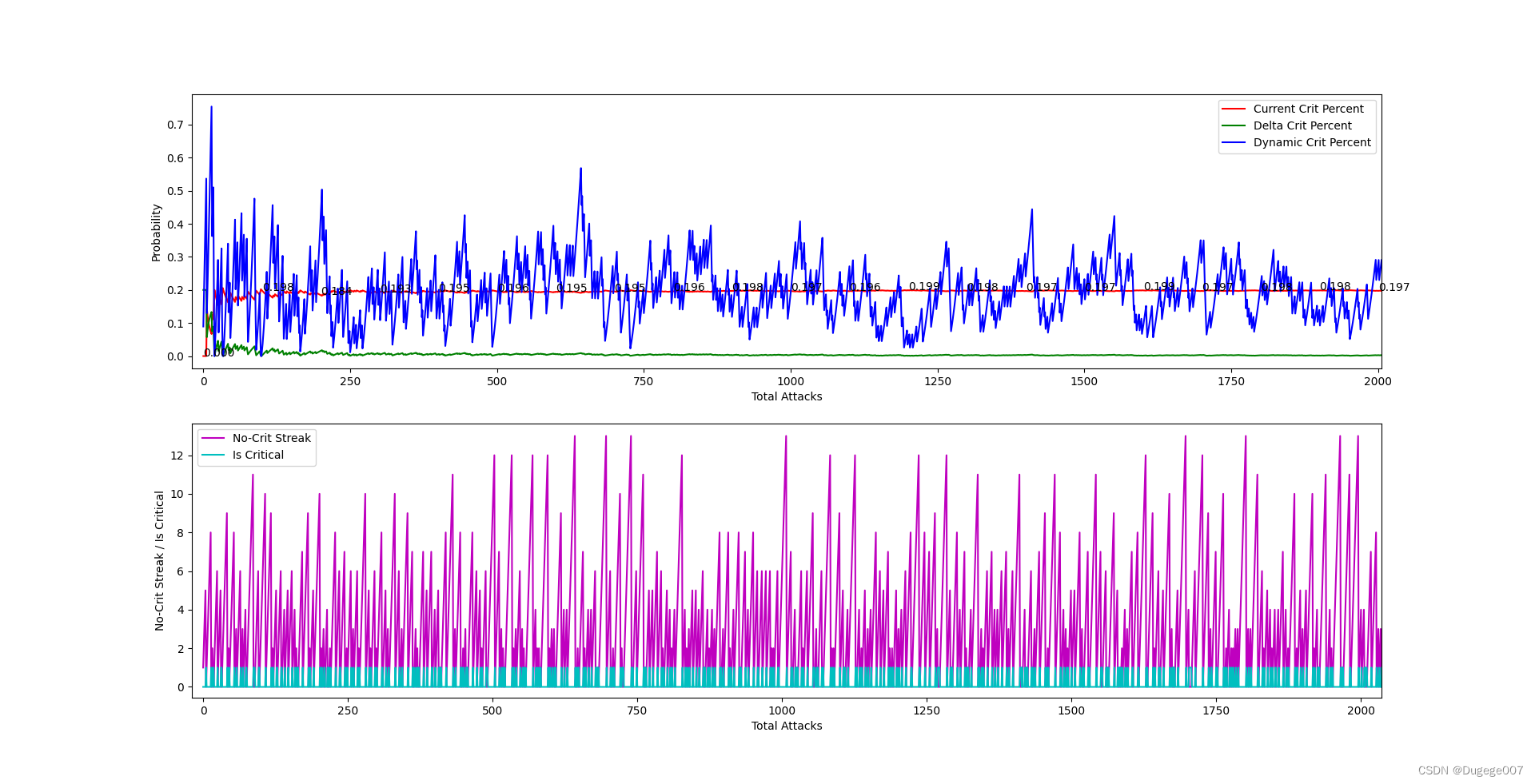
0 ~ 2000 次 如下
8000 ~ 10000 次 如下
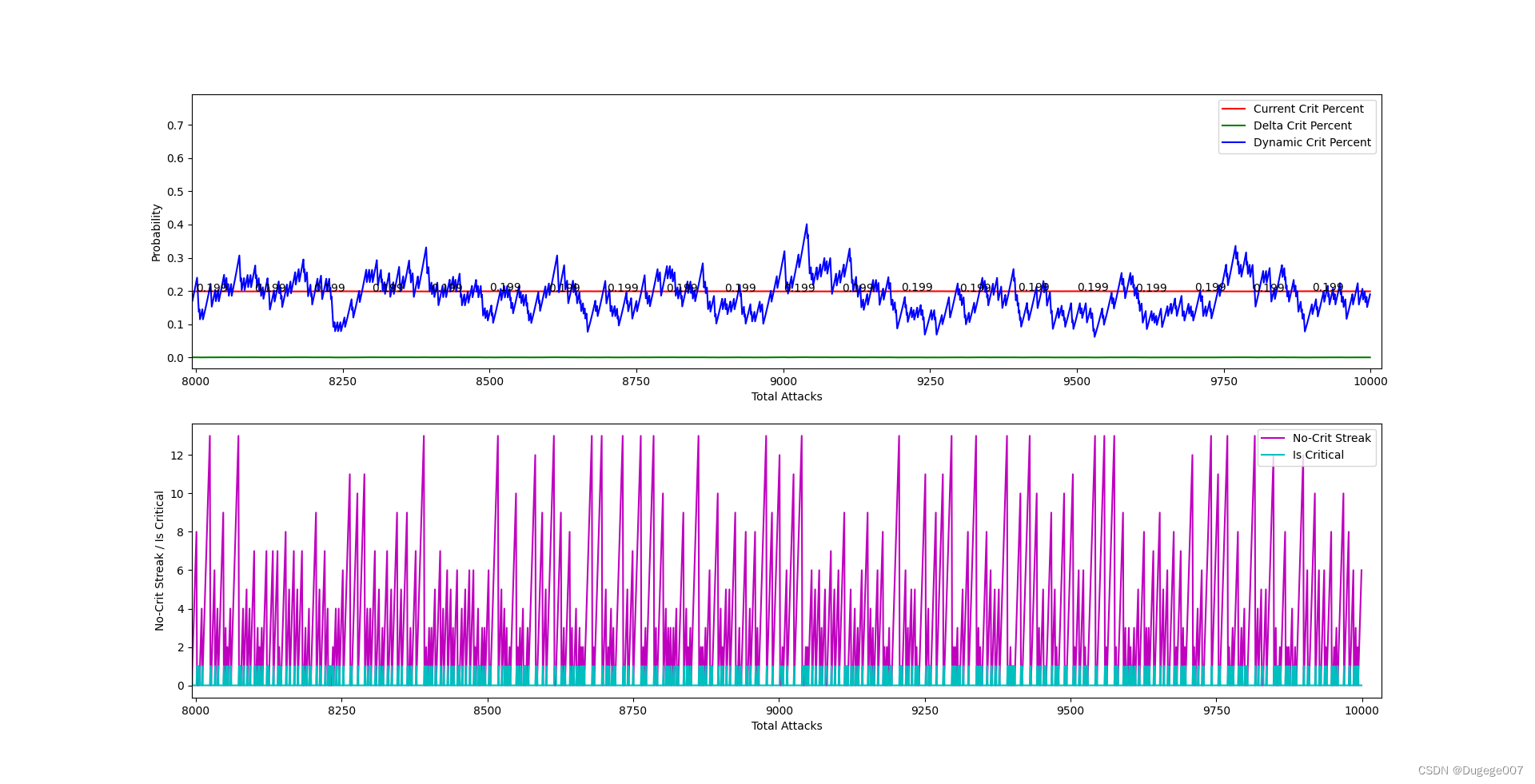
可以看出,总体暴击率会在大概300次内稳定下来,并且逐渐逼近 0.2;
在攻击次数足够多时,“动态暴击率”的浮动也会趋于稳定。
这是一种通过调整每次攻击的暴击率,来达到动态平衡效果的算法;
也可以说,这是一种动态调整每次概率,以达到目标数学期望的算法。
核心思路
以“暴击率”为例,以下是这种“动态平衡概率”算法的核心思路:
基本参数:
初始概率(目标概率) : P 动态概率 : d y n a m i c P 当前概率 : c u r r e n t P 概率差值 : d e l t a P 攻击次数 : a t t a c k N 暴击次数 : c r i t N 连续未暴击次数 : n o C r i t S t r e a k \begin{align*} \text{初始概率(目标概率)} & :P \\ \text{动态概率} & :dynamicP \\ \text{当前概率} & :currentP \\ \text{概率差值} & :deltaP \\ \text{攻击次数} & :attackN \\ \text{暴击次数} & :critN \\ \text{连续未暴击次数} & :noCritStreak \\ \end{align*} 初始概率(目标概率)动态概率当前概率概率差值攻击次数暴击次数连续未暴击次数:P:dynamicP:currentP:deltaP:attackN:critN:noCritStreak
核心运算逻辑:
c u r r e n t P = c r i t N a t t a c k N d e l t a P = ∣ P − c u r r e n t P ∣ d y n a m i c P = ( a t t a c k N ⋅ ( P − c u r r e n t P ) + c u r r e n t P ) ⋅ d e l t a P \begin{align*} currentP &= \frac{critN}{attackN} \\ deltaP &= |P - currentP| \\ dynamicP &= \left( attackN · (P - currentP) + currentP \right) · \sqrt{deltaP} \\ \end{align*} currentPdeltaPdynamicP=attackNcritN=∣P−currentP∣=(attackN⋅(P−currentP)+currentP)⋅deltaP
暴击判断逻辑:
找到一个最佳的N, 用于判断连续 N - 1 次未暴击 : Find_Optimal_N ( p ) : ( 1 − p ) N ≤ 0.05 随机数生成和暴击判断 : 如果 n o C r i t S t r e a k < N − 1 ,则生成一个随机数 p e r c e n t ; ﹂如果 p e r c e n t ≤ d y n a m i c P ,则判定为暴击,相关参数 + 1 ﹂否则 未暴击,相关参数 + 1 否则 必然暴击,相关参数 + 1 \begin{align*} \\ \text{找到一个最佳的N,} \\ \text{用于判断连续 N - 1 次未暴击} & : \\ \text{Find\_Optimal\_N}(p) & : (1 - p) ^ N \leq 0.05 \\ \\ \text{随机数生成和暴击判断} & : \\ & \text{如果 \(noCritStreak\) \( < N - 1 \),则生成一个随机数 \(percent\);} \\ & \text{ ﹂如果 \(percent\) \( \leq \) \(dynamicP\),则判定为暴击,相关参数 + 1} \\ & \text{ ﹂否则 未暴击,相关参数 + 1} \\ & \text{否则 必然暴击,相关参数 + 1} \\ \end{align*} 找到一个最佳的N,用于判断连续 N - 1 次未暴击Find_Optimal_N(p)随机数生成和暴击判断::(1−p)N≤0.05:如果 noCritStreak <N−1,则生成一个随机数 percent; ﹂如果 percent ≤ dynamicP,则判定为暴击,相关参数 + 1 ﹂否则 未暴击,相关参数 + 1否则 必然暴击,相关参数 + 1
本文到这里其实就结束了,这套算法虽然简单,但是笔者发现它的过程还是挺有意思的。
感兴趣的朋友可以继续往下看,文末还有一些优化思路…
发现
还是前文中的需求:
A. 暴击率总体为20%
B. 要求每十次攻击,至少有一次暴击
C. 要求暴击的总体分布较为均匀
假如每次暴击的概率都是0.2,并且每十次攻击至少一次暴击,这样相当于增加了总体最终的暴击数,也就是变相增加了暴击率,确实需要通过某种方式将最终结果调整到0.2.
目前笔者想到的实现方式大致分为两种:
一种是“动态概率”,我们可以随着实际已出现的概率,动态地调整下一次的概率,并保证在最终结果上符合我们的目标概率。
另一种是提前将“随机种子”做好。在制作“种子”时使用连续分段的、适当长度的数组,每段数组中目标出现的概率基本相同,且总体概率符合我们的目标概率。再人为打乱每段数组,最后将他们拼接起来。但是这种方式还有个问题,就是打乱数组之后可能会出现两个数组中的一个暴击在头一个在尾,两次暴击又会间隔较远的情况,无法完全保证 B 条件成立。
本文先尝试第一种方式————“动态概率”
以前面的需求为例,假如每次暴击的概率都是0.2,并且每十次攻击至少一次暴击,先这样在Unity中看一下最终的暴击率会高出多少
using UnityEngine;public class CriticalHit : MonoBehaviour
{// 初始暴击率public float InitCritPercent = 0.2f;// 当前暴击概率private float currentCritPercent;// 当前总攻击次数private int attackTotalCount = 0;// 当前总暴击过的次数private int critTotalCount = 0;// 连续未出现暴击的次数private int noCritStreakCount = 0;private void Start(){currentCritPercent = InitCritPercent;}private void Update(){// 监听鼠标左键输入if (Input.GetMouseButtonDown(0)){// 测试一次PerformAttack();Debug.Log("当前暴击率:" + currentCritPercent);}if (Input.GetKeyDown(KeyCode.Space)){// 测试一万次for (int i = 0; i < 10000; i++) PerformAttack();}}private void PerformAttack(){attackTotalCount++;bool isCritical = false;if (attackTotalCount > 0){// 计算当前暴击概率 = 总暴击数 / 总攻击数currentCritPercent = (float)critTotalCount / attackTotalCount;}// 检查是否需要强制暴击if (noCritStreakCount < 9){float percent = Random.Range(0f, 1f);if (percent < InitCritPercent){isCritical = true;noCritStreakCount = 0; // 重置计数器}else{noCritStreakCount++;}}else{isCritical = true;noCritStreakCount = 0; // 重置计数器}if (isCritical) critTotalCount++;// 执行攻击,如果 isCritical 为 true,则为暴击if (isCritical)Debug.Log("Critical Hit!");elseDebug.Log("Normal Hit.");}
}
将这个脚本挂到场景中的空物体上,运行游戏,然后按空格键先测试一万次,再点击鼠标左键显示当前的暴击率
用上述方式测试几次,会发现最终的暴击率大概在 22.5% 左右,打印结果如下图所示
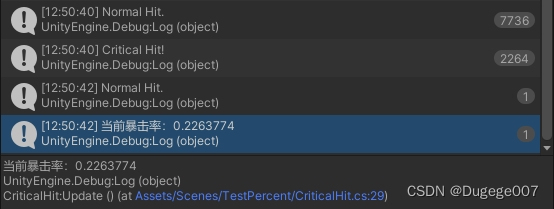
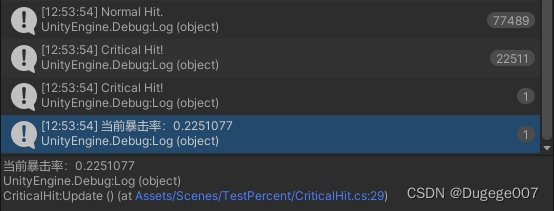
那么这多出来的 2.5% 为什么会是 2.5% 呢,它具体是怎么来的呢,如何避免它产生呢?
带着这样的疑惑,笔者开始尝试进行分析…
排除误差的可能
首先我们要排除这 2.5% 是误差的可能。
假设暴击率为 0.2,不考虑其他的设定和限制,每次测试十万次、共测试三次。
那么正常情况下的输出结果如下图所示
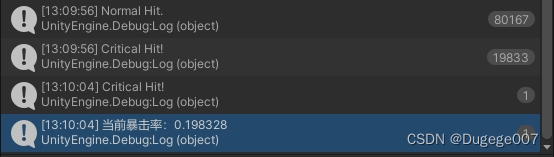
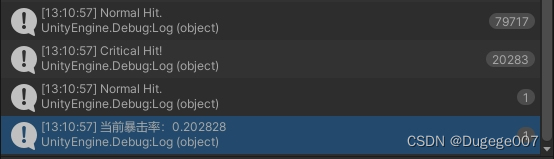
误差在 0.2% 左右,这与 2.5% 差别还是很大的,所以基本排除这是误差导致的情况。
探索
为了进一步优化算法,笔者决定结合已有的数据和个人直觉进行改进。
笔者用Python重新编写了一版代码,这样我们不仅可以方便地输出图表进行可视化分析,还能在这个基础上进行后续的代码修改和优化。
import matplotlib.pyplot as plt
import random# 初始化变量
InitCritPercent = 0.2 # 初始暴击率
attackTotalCount = 0 # 总攻击次数
critTotalCount = 0 # 总暴击次数
noCritStreakCount = 0 # 连续未暴击次数# 给 plot 准备的列表
currentCritPercentList = []
noCritStreakCountList = []
isCriticalList = []# 测试 10000 次
for i in range(10000):attackTotalCount += 1isCritical = False# 检查是否连续 9 次未暴击if noCritStreakCount < 9:percent = random.random()if percent <= InitCritPercent:isCritical = TruenoCritStreakCount = 0else:noCritStreakCount += 1else:isCritical = TruenoCritStreakCount = 0if isCritical:critTotalCount += 1# 计算当前暴击概率currentCritPercent = critTotalCount / attackTotalCount# 添加数据到列表中currentCritPercentList.append(currentCritPercent)noCritStreakCountList.append(noCritStreakCount)isCriticalList.append(int(isCritical))# 创建多表格
fig, axs = plt.subplots(2)# 画出暴击概率数据表格
axs[0].plot(currentCritPercentList, label='Current Crit Percent', color='r')
axs[0].set_xlabel('Total Attacks')
axs[0].set_ylabel('Probability')
axs[0].legend()# 每 100 条数据标注一下
for i in range(0, len(currentCritPercentList), 100):axs[0].annotate(f"{currentCritPercentList[i]:.5f}", (i, currentCritPercentList[i]))# 画出连续未暴击次数的表格
axs[1].plot(noCritStreakCountList, label='No-Crit Streak', color='m')
axs[1].plot(isCriticalList, label='Is Critical', color='c')
axs[1].set_xlabel('Total Attacks')
axs[1].set_ylabel('No-Crit Streak / Is Critical')
axs[1].legend()plt.show()
从输出的图表中不难看出,整体的暴击率确实变高了,如下图所示
前 2000 次 如下
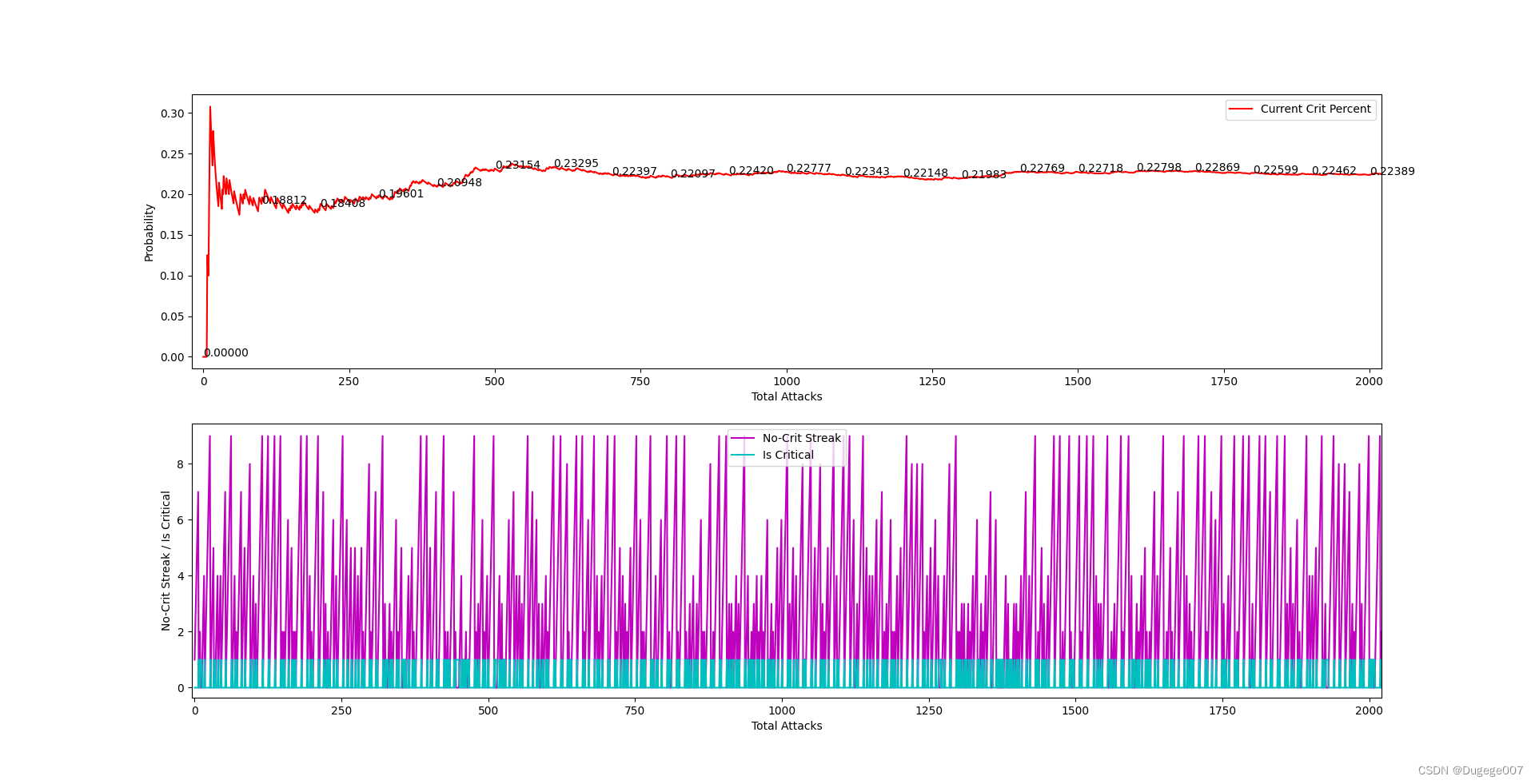
8000 ~ 10000 次 如下
如要将最终的暴击概率调整回 0.2,那就应该降低“当前暴击概率”,将 B 条件所增加的那部分修正回来。
“递增修正”
将前文的python代码添加几个变量,用来检测当前暴击概率的变化,当前暴击概率高于初始暴击率的时候,就降低动态暴击率,直到将当前暴击率拉回到正常水平;反之亦然。
import matplotlib.pyplot as plt
import random# 初始化变量
InitCritPercent = 0.2 # 初始暴击率
currentCritPercent = 0 # 当前暴击概率
deltaCritPercent = 0 # 当前暴击率与初始暴击率的差值(用来表示变化)
dynamicCritPercent = 0.2 # 动态暴击率
attackTotalCount = 0 # 总攻击次数
critTotalCount = 0 # 总暴击次数
noCritStreakCount = 0 # 连续未暴击次数# 给 plot 准备的列表
currentCritPercentList = []
deltaCritPercentList = []
dynamicCritPercentList = []
noCritStreakCountList = []
isCriticalList = []# 测试 10000 次
for i in range(10000):attackTotalCount += 1isCritical = False# 检查是否连续 9 次未暴击if attackTotalCount > 0:# 计算当前暴击概率currentCritPercent = critTotalCount / attackTotalCount# 计算当前暴击概率与初始暴击率的差值deltaCritPercent = abs(InitCritPercent - currentCritPercent)# 计算动态暴击率if(currentCritPercent > InitCritPercent):dynamicCritPercent -= deltaCritPercentif(currentCritPercent < InitCritPercent):dynamicCritPercent += deltaCritPercent# 检查是否连续 9 次未暴击if noCritStreakCount < 9:percent = random.random()if percent <= dynamicCritPercent:isCritical = TruenoCritStreakCount = 0else:noCritStreakCount += 1else:isCritical = TruenoCritStreakCount = 0if isCritical:critTotalCount += 1# 将数据添加到列表中currentCritPercentList.append(currentCritPercent)deltaCritPercentList.append(deltaCritPercent)dynamicCritPercentList.append(dynamicCritPercent)noCritStreakCountList.append(noCritStreakCount)isCriticalList.append(int(isCritical))# 创建多表格
fig, axs = plt.subplots(2)# 每 100 条数据标注一下
for i in range(0, len(currentCritPercentList), 100):axs[0].annotate(f"{currentCritPercentList[i]:.3f}", (i, currentCritPercentList[i]))# 画出暴击概率数据表格
axs[0].plot(currentCritPercentList, label='Current Crit Percent', color='r')
axs[0].plot(deltaCritPercentList, label='Delta Crit Percent', color='g')
axs[0].plot(dynamicCritPercentList, label='Dynamic Crit Percent', color='b')
axs[0].set_xlabel('Total Attacks')
axs[0].set_ylabel('Probability')
axs[0].legend()# 画出连续未暴击次数的表格
axs[1].plot(noCritStreakCountList, label='No-Crit Streak', color='m')
axs[1].plot(isCriticalList, label='Is Critical', color='c')
axs[1].set_xlabel('Total Attacks')
axs[1].set_ylabel('No-Crit Streak / Is Critical')
axs[1].legend()plt.show()
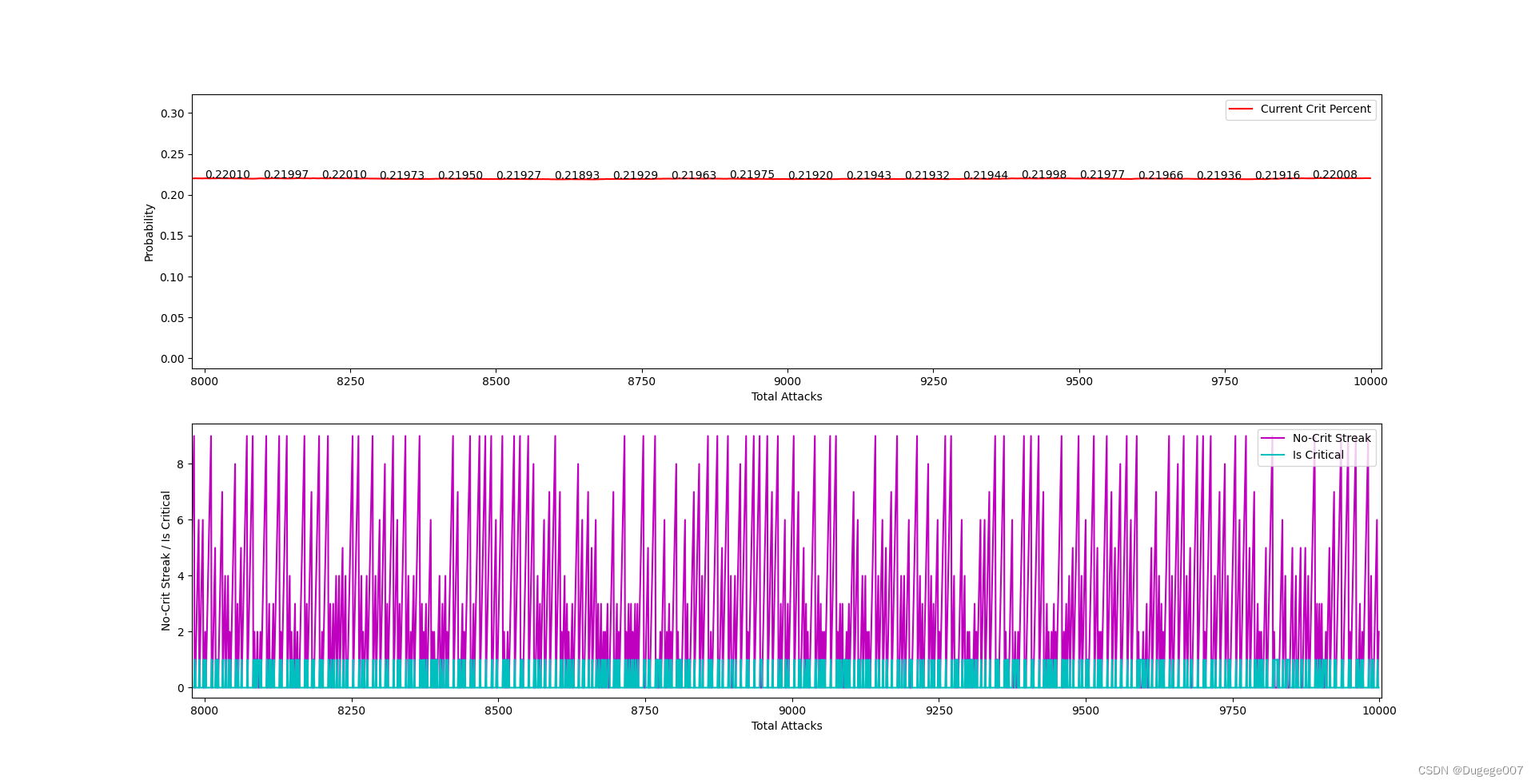
输出结果如下图所示
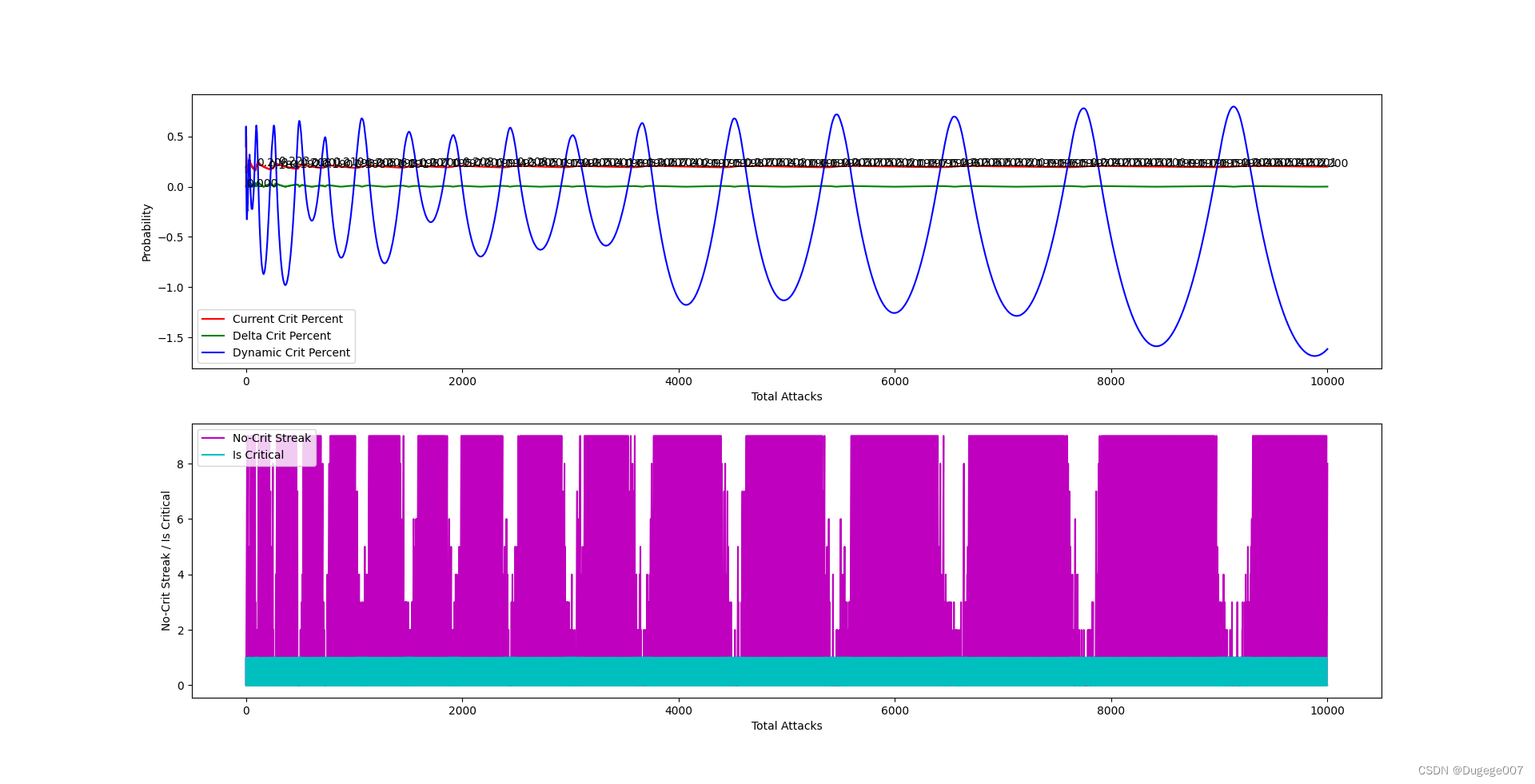
前 2000 次 如下
可以明显看出动态暴击率在大幅度地反复震荡,并且明显超出了 (0, 1) 的区间;
在震荡的高点时,会出现连续暴击的情况;在震荡的低点时,会出现连续地触发“保底”暴击;
这样虽然能将总体暴击概率稳定在 0.2 左右,但这显然不满足条件 C。
“递增修正”优化
显而易见,当动态暴击率超出 (0, 1) 区间时,就和 0、1 没有区别了
所以可以为它加个简单限幅,例如笔者将动态暴击率的幅度限制在(0.5倍初始暴击率,2倍初始暴击率)之间
# 同上文代码# 测试 10000 次
for i in range(10000):# 同上文代码if attackTotalCount > 0:# 同上文代码# 计算动态暴击率if(currentCritPercent > InitCritPercent):dynamicCritPercent = min(max(dynamicCritPercent - deltaCritPercent, InitCritPercent * 0.5), InitCritPercent * 2)if(currentCritPercent < InitCritPercent):dynamicCritPercent = min(max(dynamicCritPercent + deltaCritPercent, InitCritPercent * 0.5), InitCritPercent * 2)# 检查是否连续 9 次未暴击if noCritStreakCount < 9:# 同上文代码# 同上文代码# 同上文代码
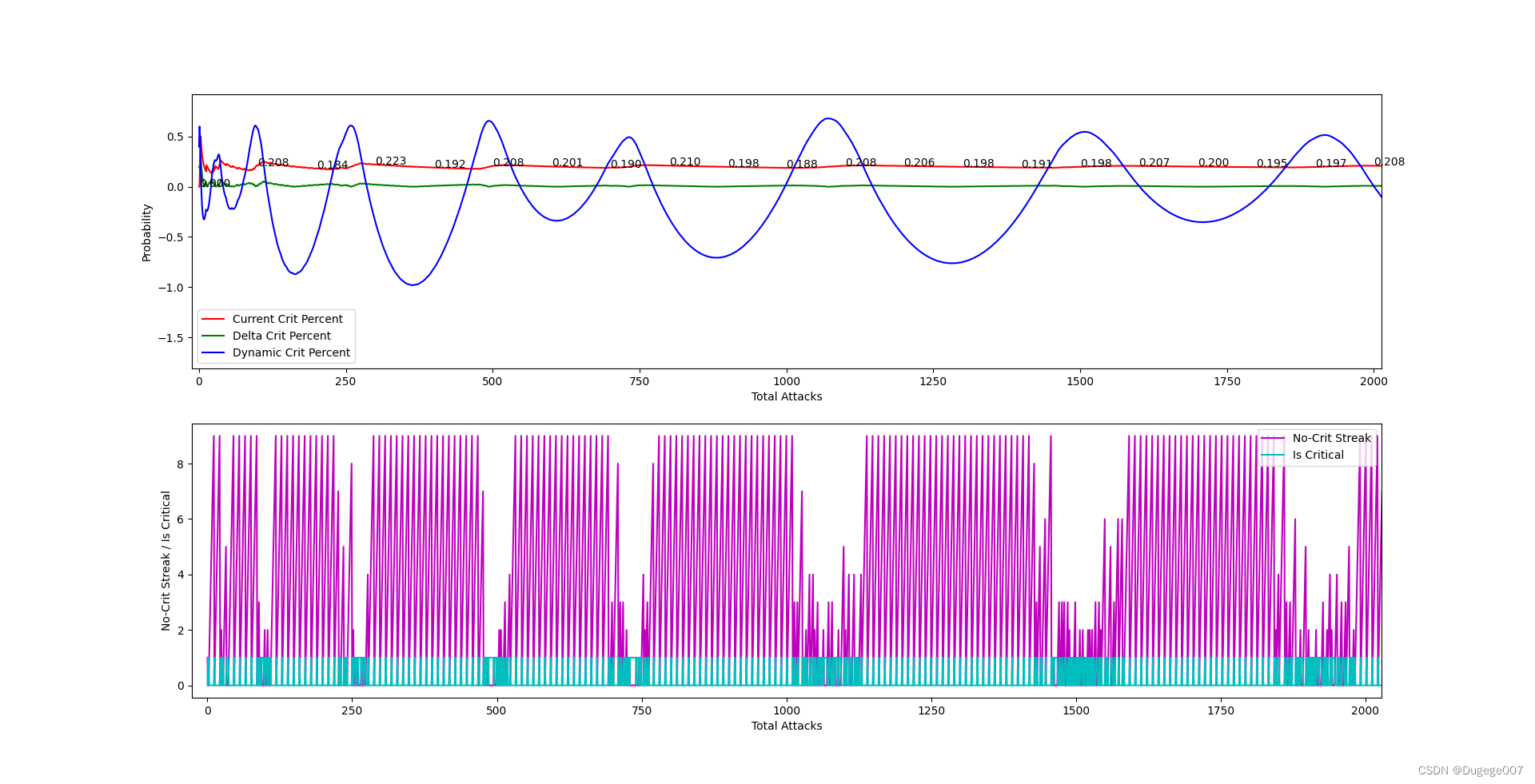
输出结果如下图所示
前 2000 次 如下
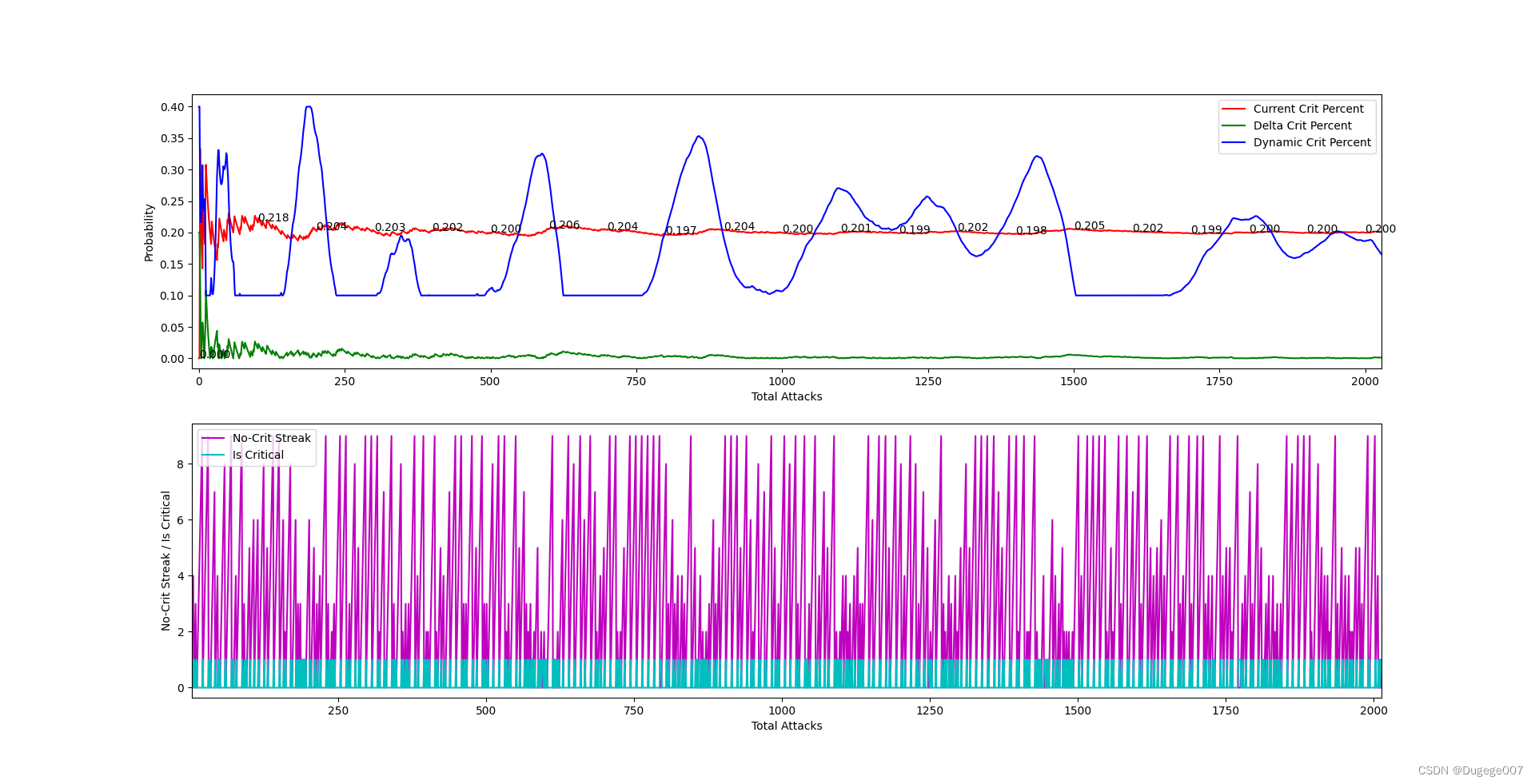
8000 ~ 10000 次 如下
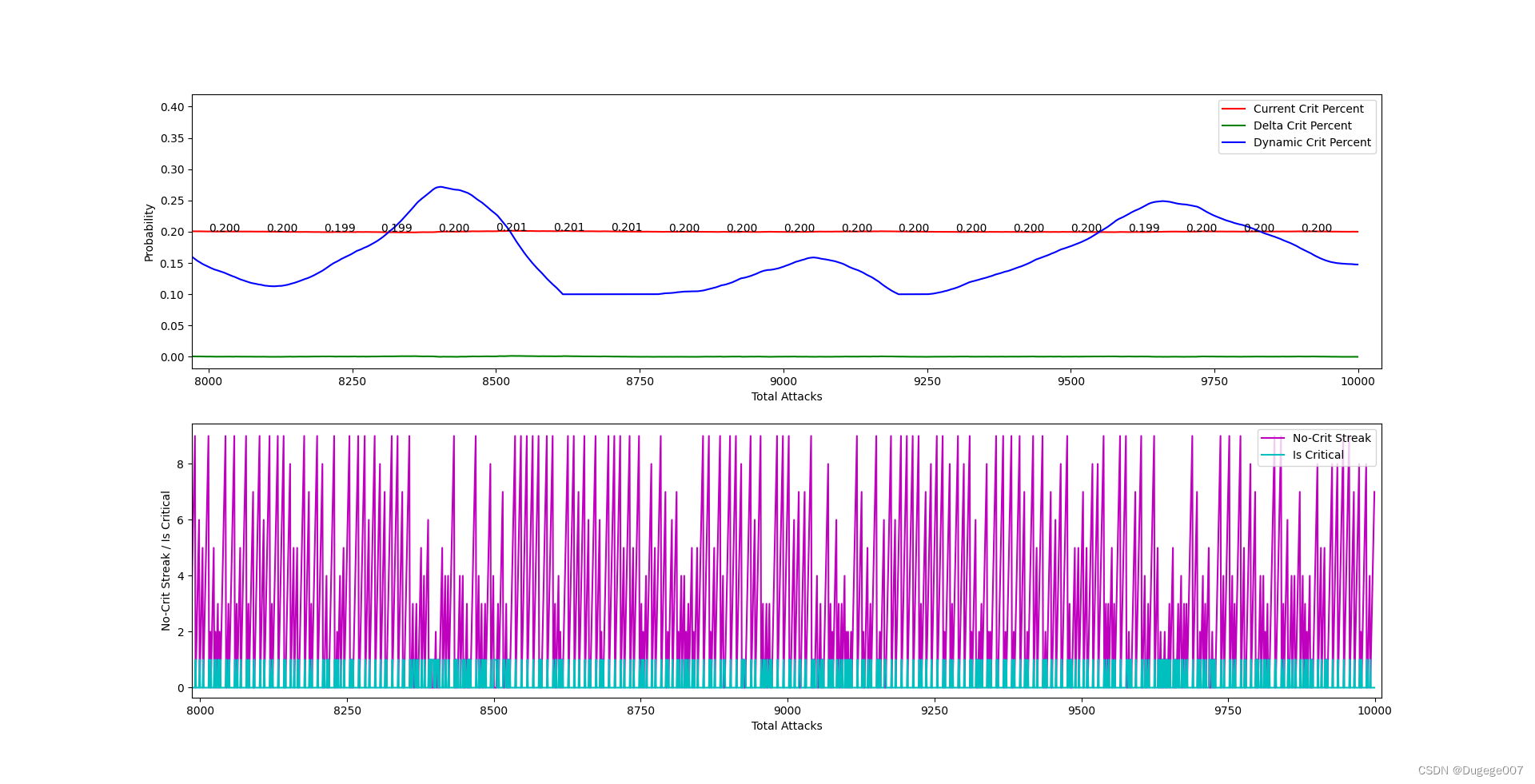
现在的算法已经基本可用了,但还需要多尝试才能找到合适的限幅范围。
当限幅范围过大时,概率的分布会变得不均匀;
限幅范围过小时,又会出现无法逼近目标概率(初始暴击率),比较麻烦。
“递增修正”测试
将上述优化过的算法应用到其他情景中,例如掷硬币,每5次投掷至少有一次正面
初始概率(目标概率) = 0.5
# 同上文代码
InitCritPercent = 0.5
dynamicCritPercent = 0.5
# 同上文代码# 测试 10000 次
for i in range(10000):# 同上文代码# 检查是否连续 4 次未掷出正面if noCritStreakCount < 4:# 同上文代码# 同上文代码# 同上文代码
输出结果如下图所示
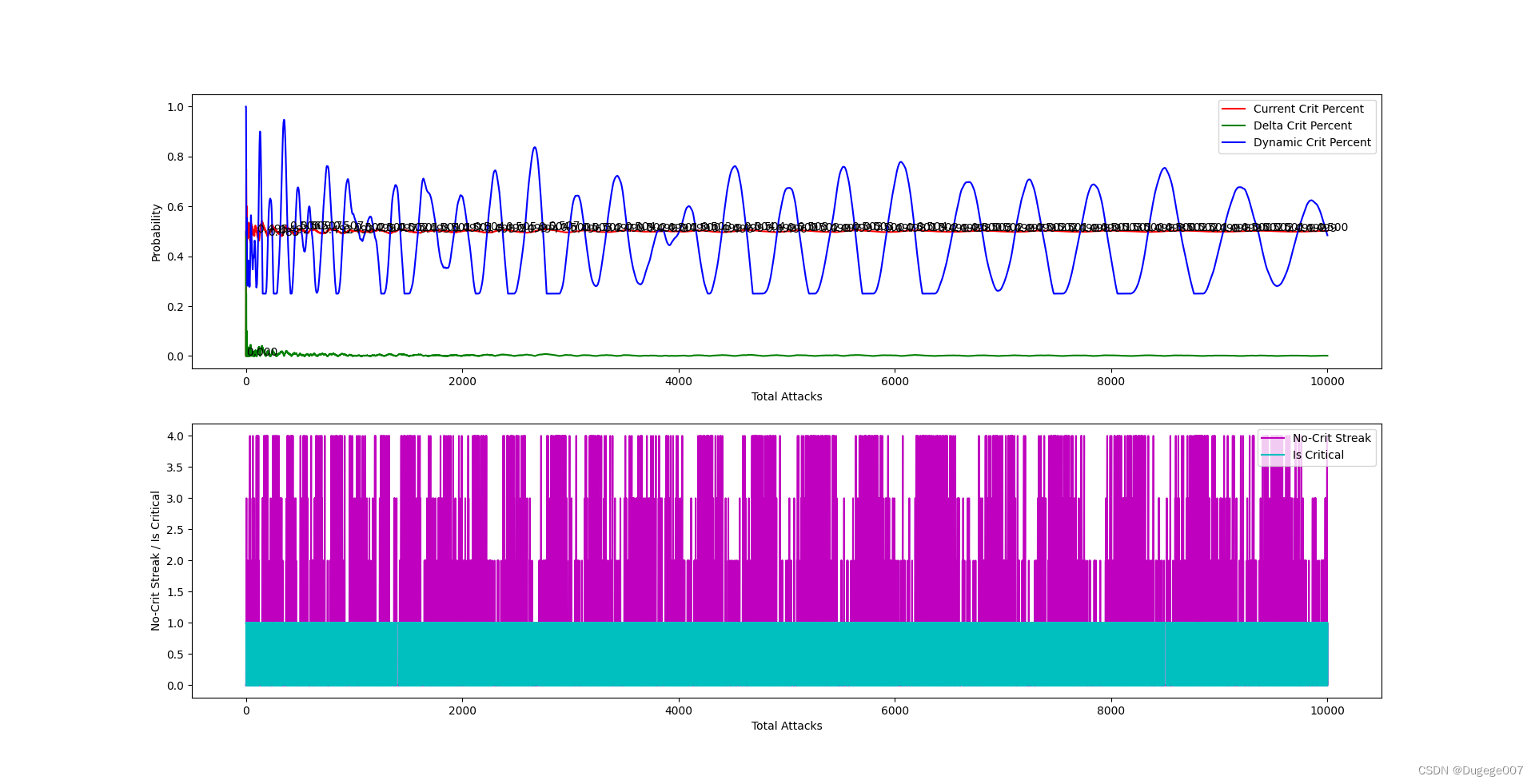
前 2000 次 如下
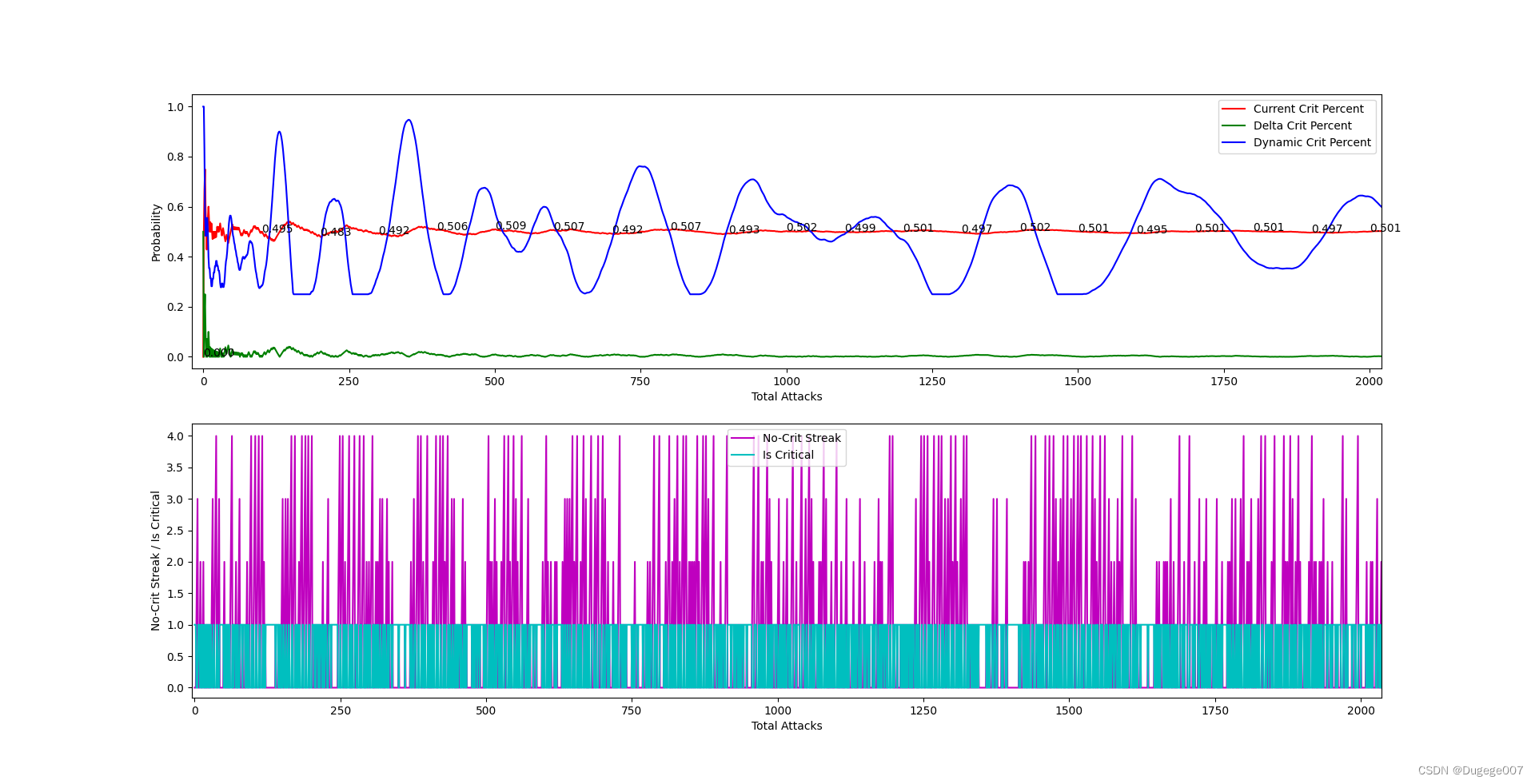
8000 ~ 10000 次 如下
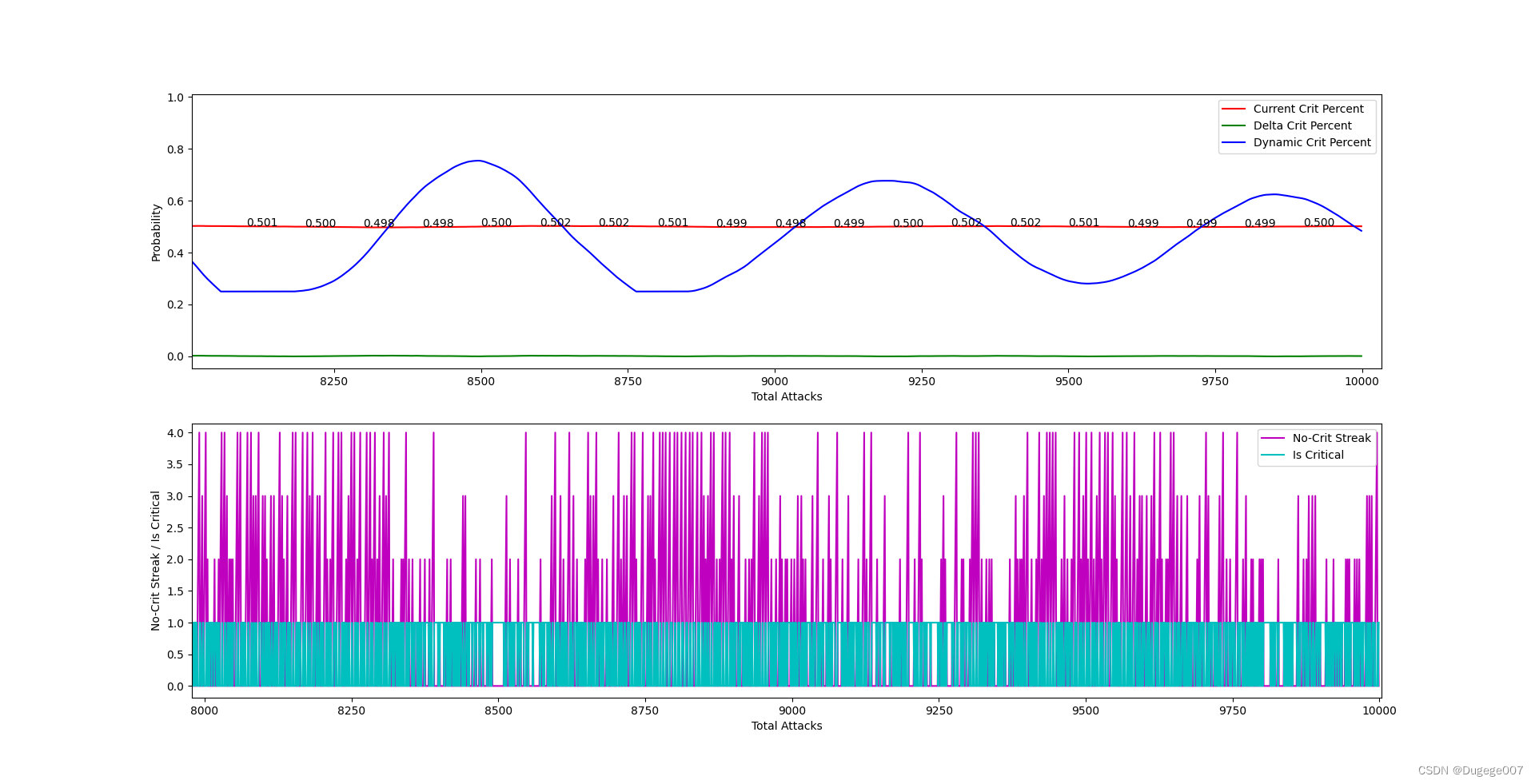
可以发现出现连续未正面的次数(连续未暴击次数),又在动态概率的波谷处出现“聚拢”现象,这很好理解:因为我们的限幅有些过大了。
总结下来,这种手动限定幅度的方式效率很低还容易出问题…
那么能不能让它根据自身目前状况,如目标概率、总攻击次数等参数,来动态调整 动态暴击率的增量呢?
“镜像修正”
基于以上思考,笔者希望每次攻击的“动态暴击率”是上次“当前暴击概率”关于“初始暴击率”的镜像,通过这种有针对性的“反向”操作,来将最终暴击率逼近目标值。
于是便有如下代码:
# 初始化变量
InitCritPercent = 0.2 # 初始暴击率
dynamicCritPercent = 0.2 # 动态暴击率
# 同上文代码# 测试 10000 次
for i in range(10000):# 同上文代码if attackTotalCount > 0:# 同上文代码# 计算动态暴击率dynamicCritPercent = attackTotalCount * InitCritPercent - (attackTotalCount - 1) * currentCritPercent# 检查是否连续 9 次未暴击if noCritStreakCount < 9:# 同上文代码# 同上文代码# 同上文代码
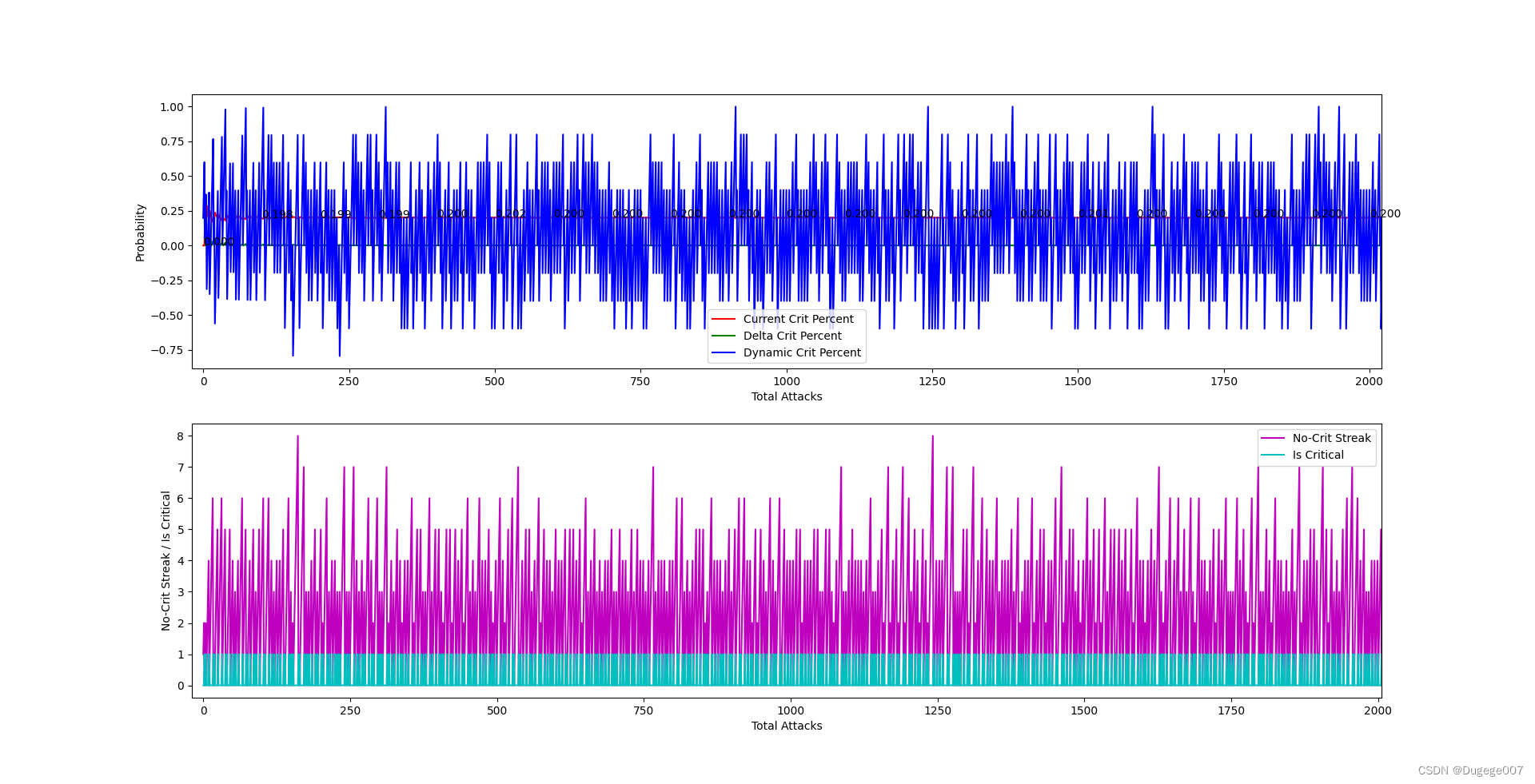
输出结果如下图所示
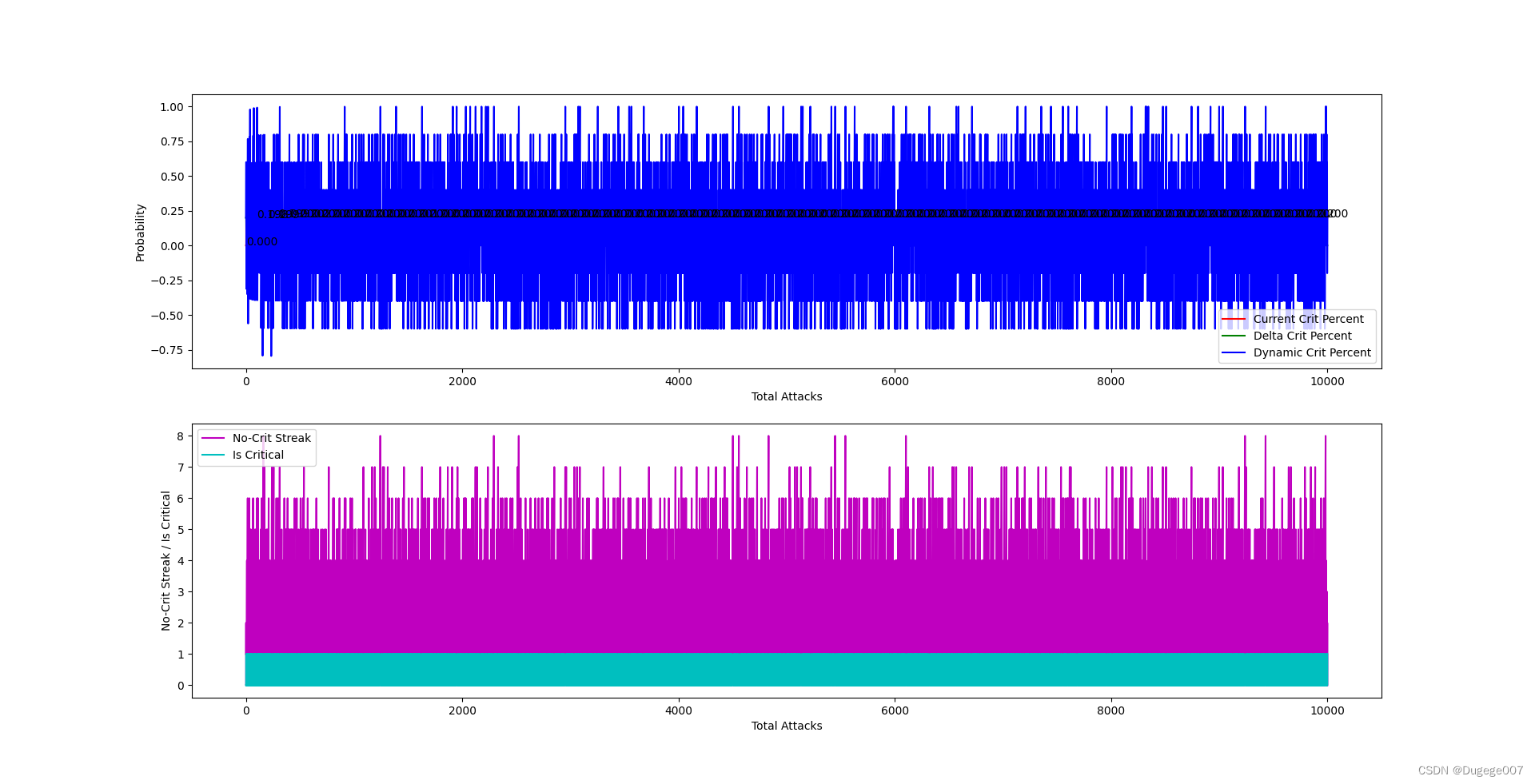
前 2000 次 如下
8000 ~ 10000 次 如下
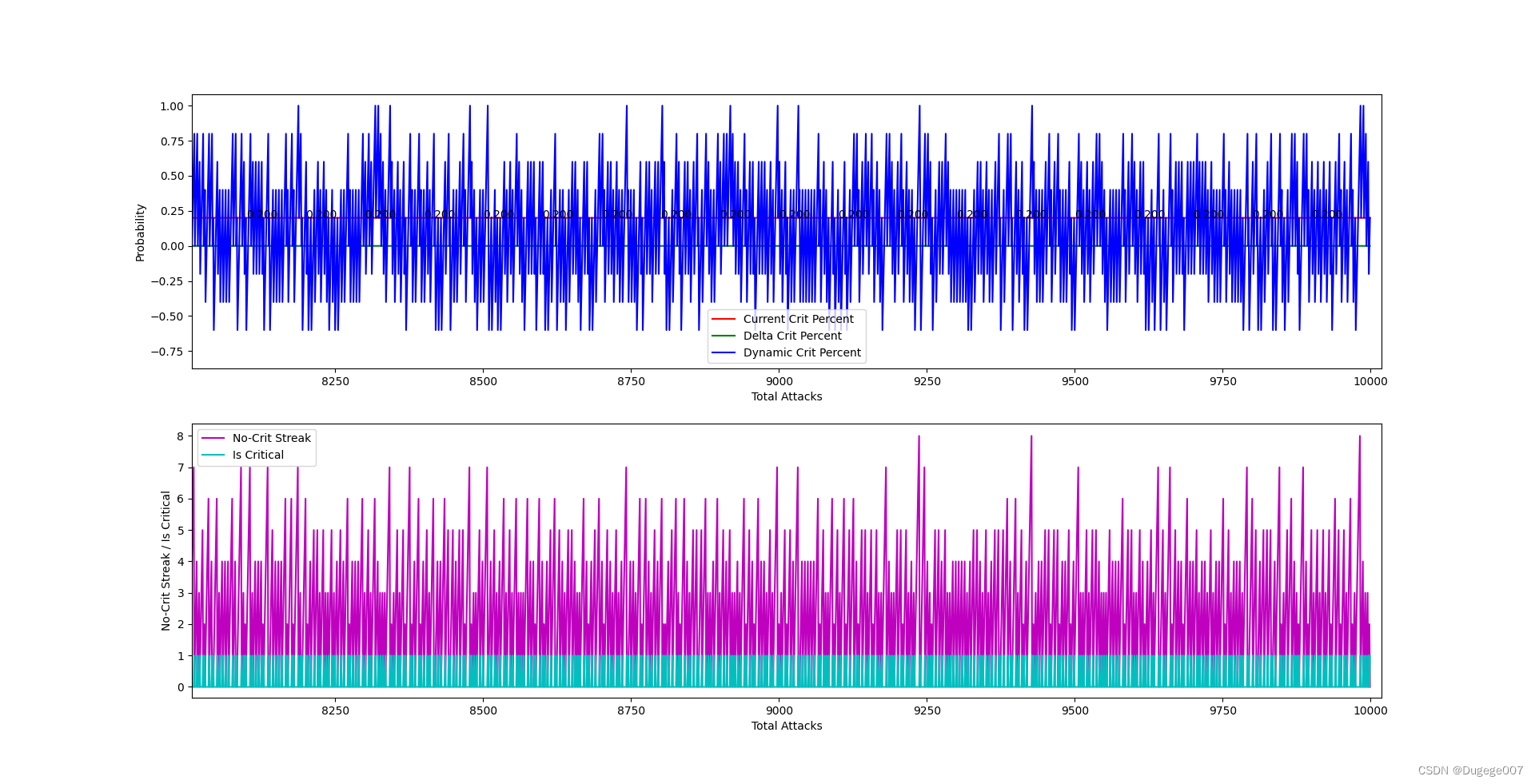
虽然能将最终的暴击概率稳定在 0.2,但结果过于平均了!
可以说这种“修正”的操作过于灵敏,导致暴击的分布非常均匀,甚至没有出现连续 9 次以上的未暴击。但这仍不是我们想要的,需要继续优化。
“镜像修正”优化
笔者发现,这种“过于均匀”的分布情况也是因为每次修正幅度过大导致的。
现在要调整这个幅度会比“递增修正”的方法容易很多,只需要让“计算动态暴击率”的结果乘以一个较小的系数即可。
这个系数需要与当前的状态有关,并且是一个越来越小的值。
而在攻击次数越来越多时,currentCritPercent 也会越来越逼近 InitCritPercent 的值,所以 deltaCritPercent 会随着攻击次数的增多越来越小;
(又因为 currentCritPercent 趋向于一个比 InitCritPercent 偏大的值,那么 deltaCritPercent 也会永不为 0)
这里我们就用 deltaCritPercent 来作为系数,目前来看刚好合适。
# 同上文代码# 计算动态暴击率dynamicCritPercent = (attackTotalCount * (InitCritPercent - currentCritPercent) + currentCritPercent) * deltaCritPercent# 同上文代码
输出结果如下图所示
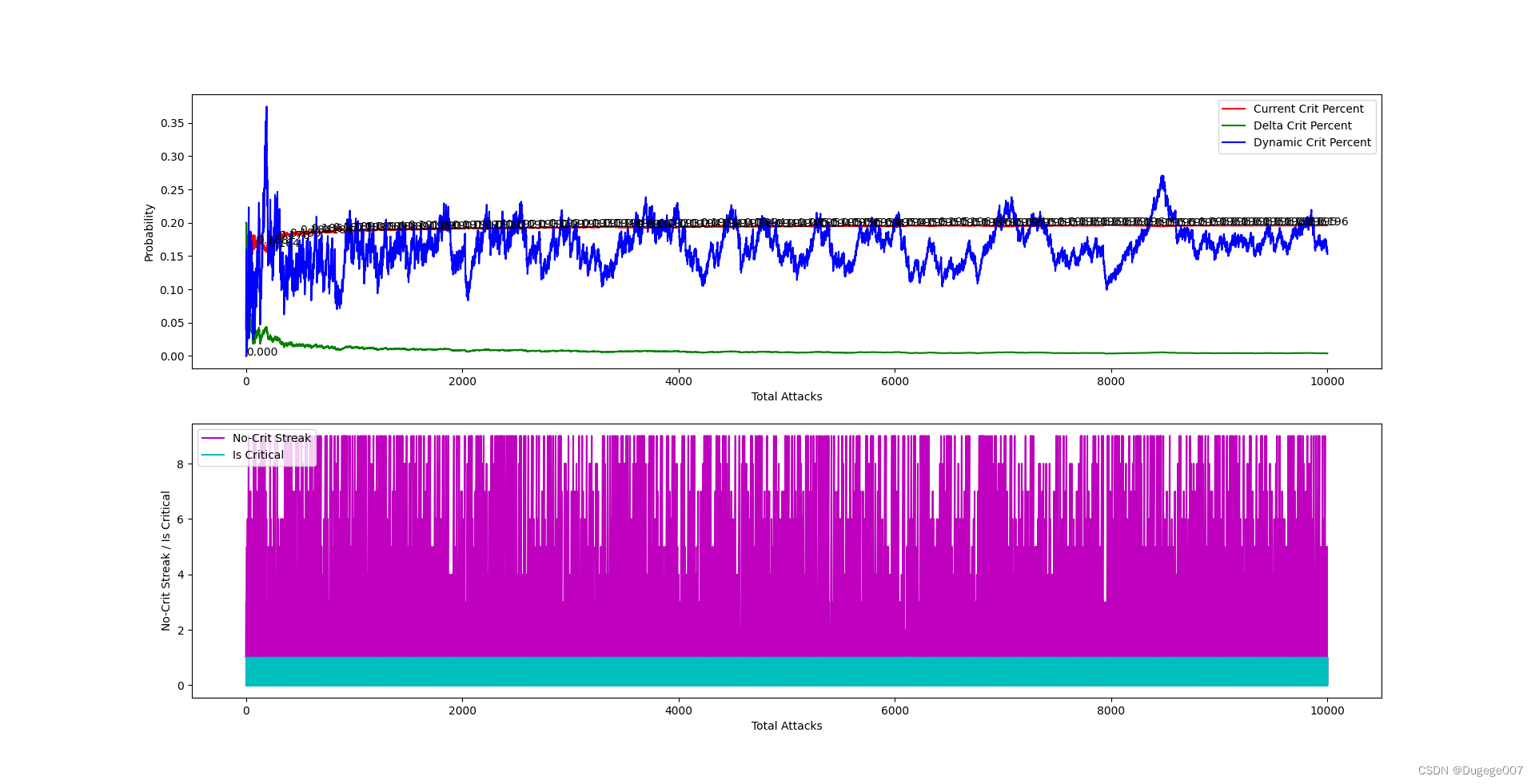
前 2000 次 如下
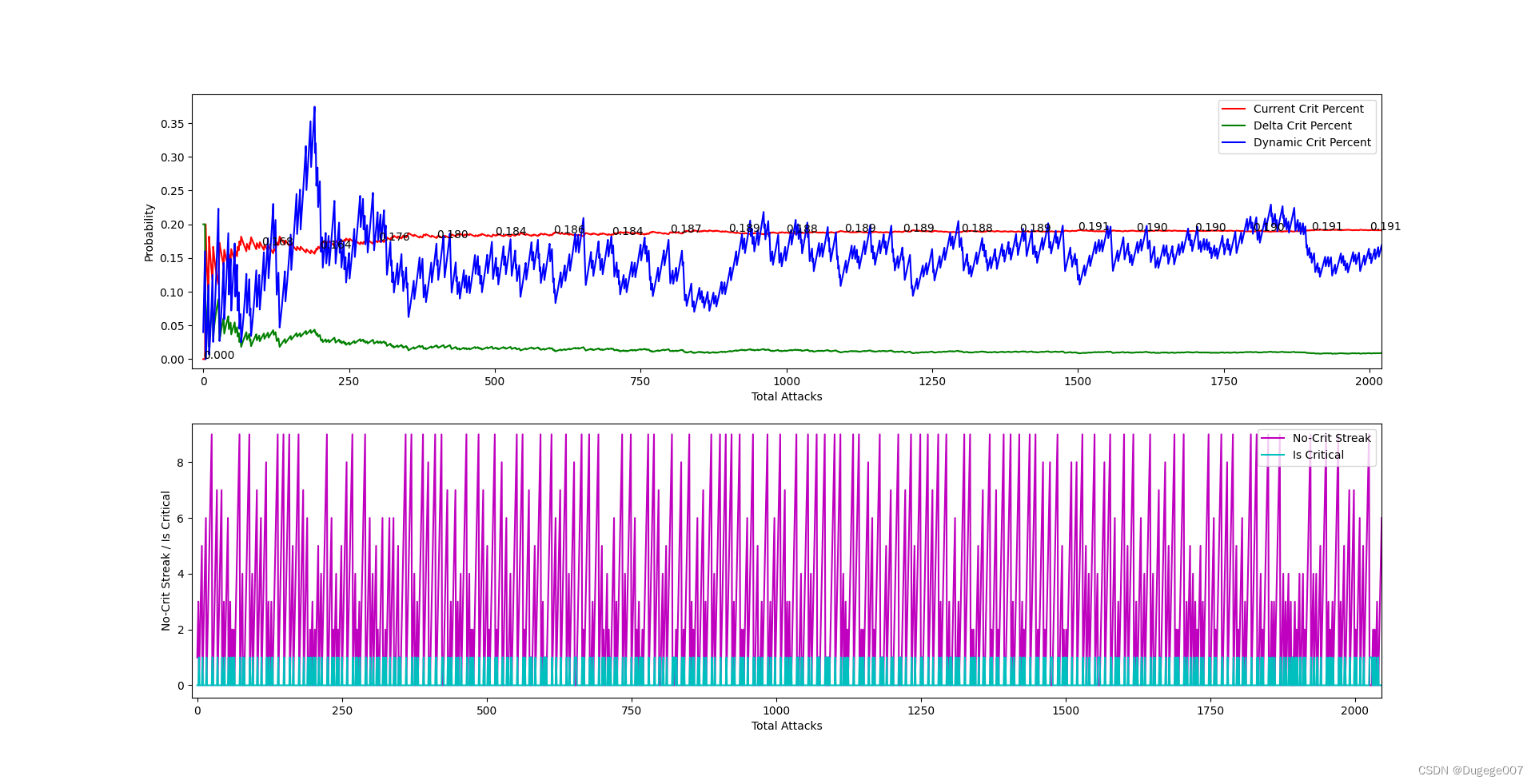
8000 ~ 10000 次 如下
由于对每次的 dynamicCritPercent 的幅度都做了差不多的限制,可以看到图二中,在前 1000 次左右攻击时,currentCritPercent 逼近目标值的速度很慢。
啧,还差一点…
继续优化!既然 deltaCritPercent 会随着攻击次数增多变得越来越小,那么我们不妨直接将它放大。
# 同上文代码# 计算动态暴击率dynamicCritPercent = (attackTotalCount * (InitCritPercent - currentCritPercent) + currentCritPercent) * pow(deltaCritPercent, 0.5)# 同上文代码
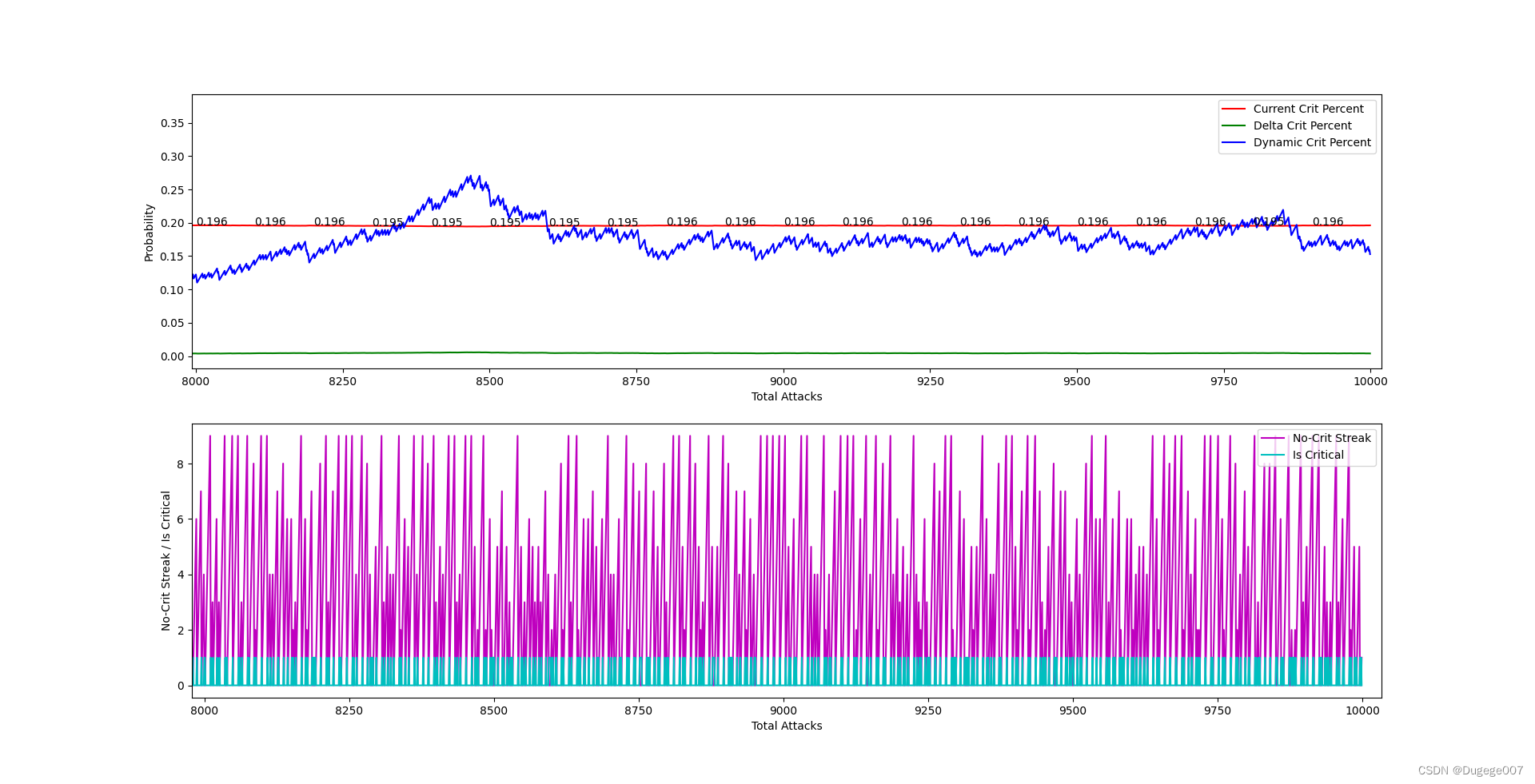
输出结果如下图所示
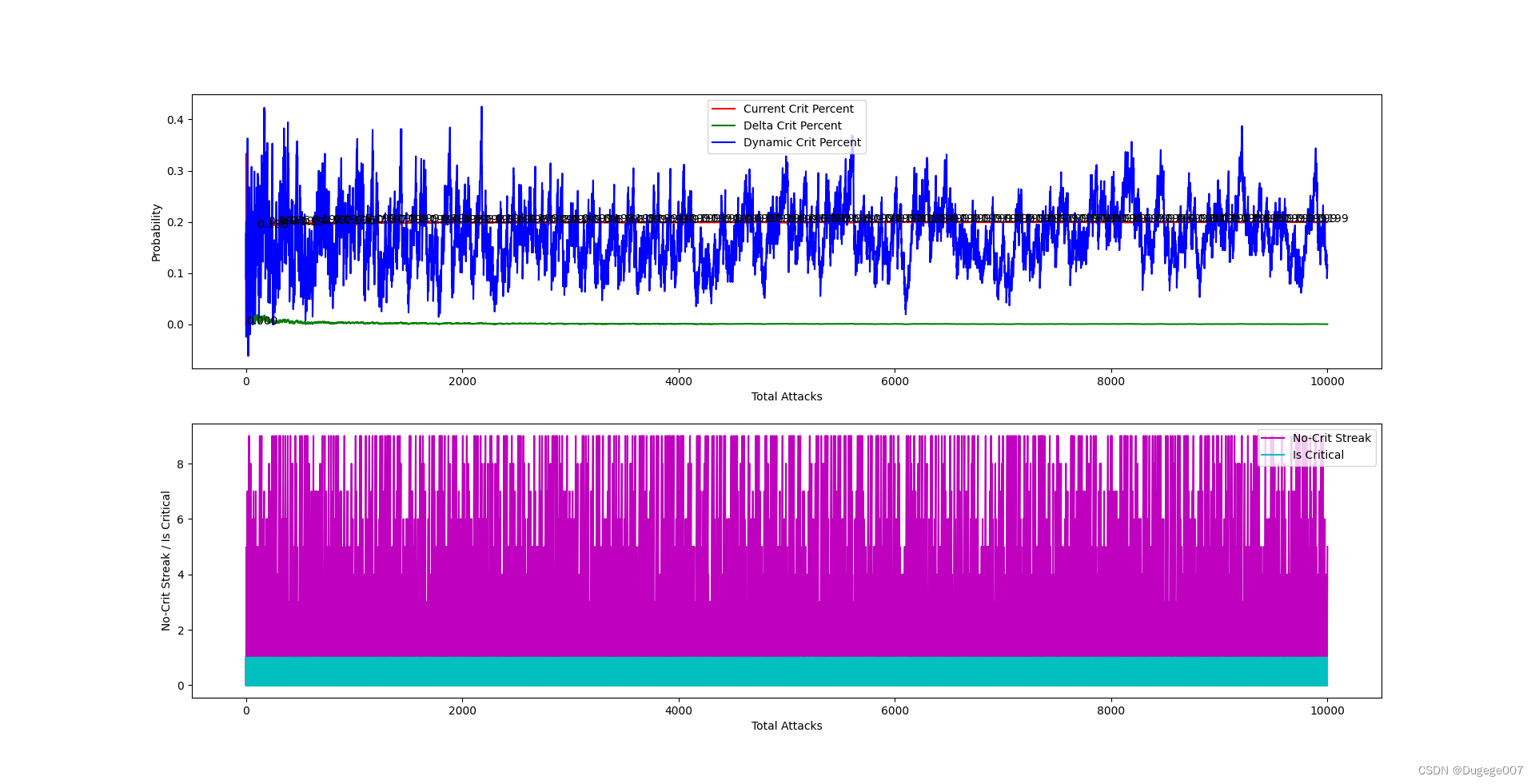
前 2000 次 如下
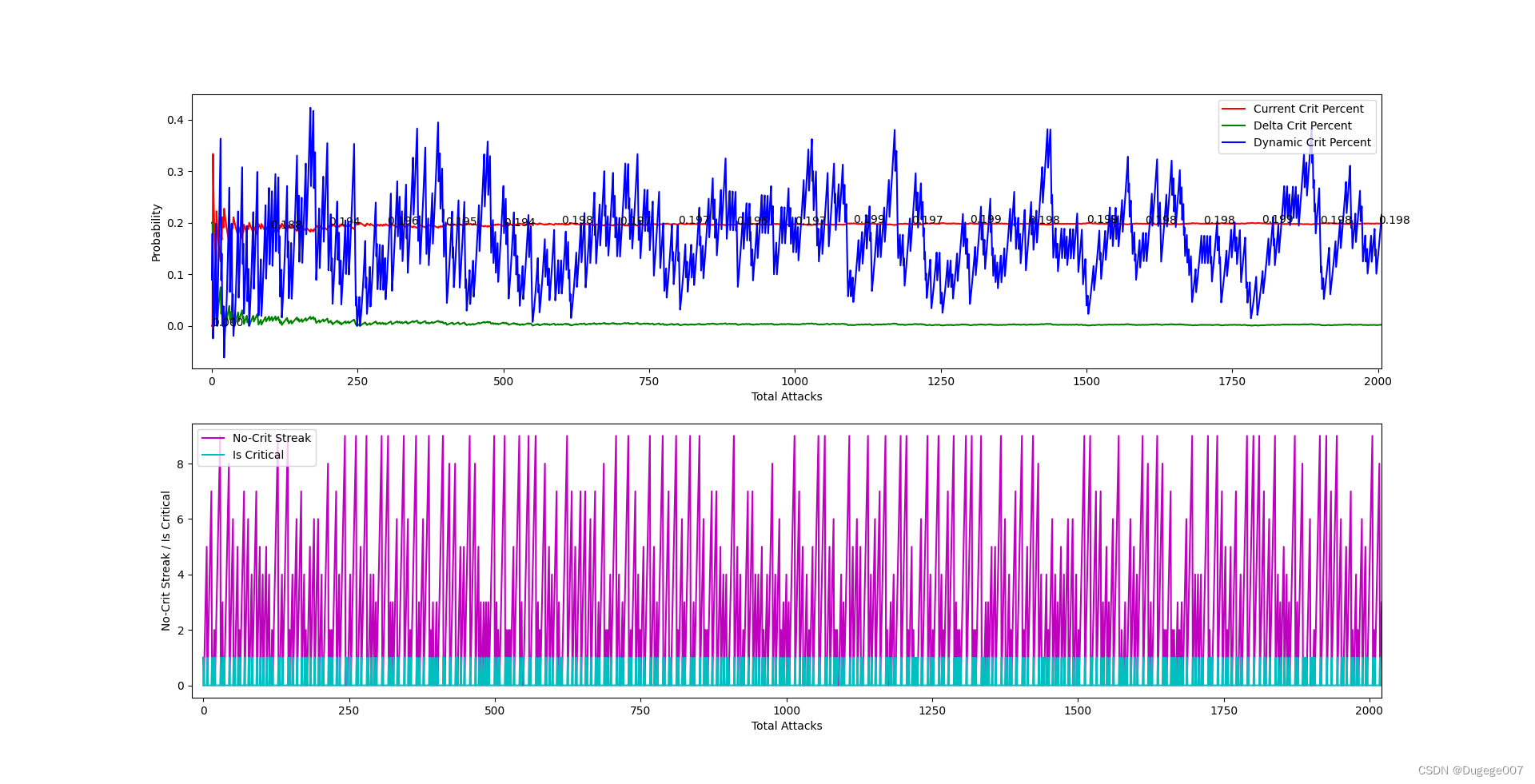
8000 ~ 10000 次 如下
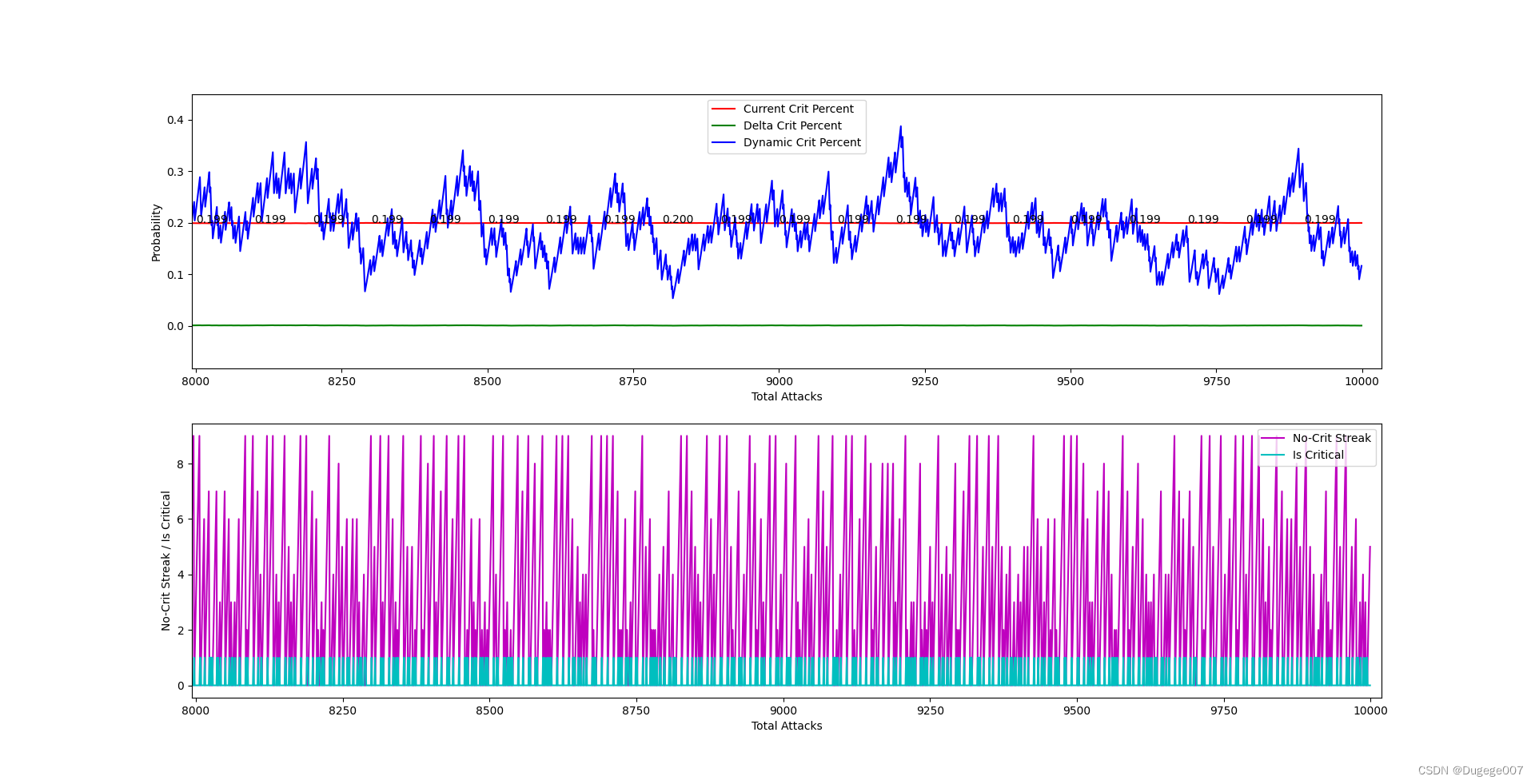
以上结果已经基本符合预期。
“镜像修正”测试
掷硬币
下面还是用硬币的例子:掷硬币,每5次投掷至少有一次正面
初始概率(目标概率) = 0.5
# 同上文代码
InitCritPercent = 0.5
dynamicCritPercent = 0.5
# 同上文代码# 测试 10000 次
for i in range(10000):# 同上文代码# 检查是否连续 4 次未掷出正面if noCritStreakCount < 4:# 同上文代码# 同上文代码# 同上文代码
输出结果如下图所示
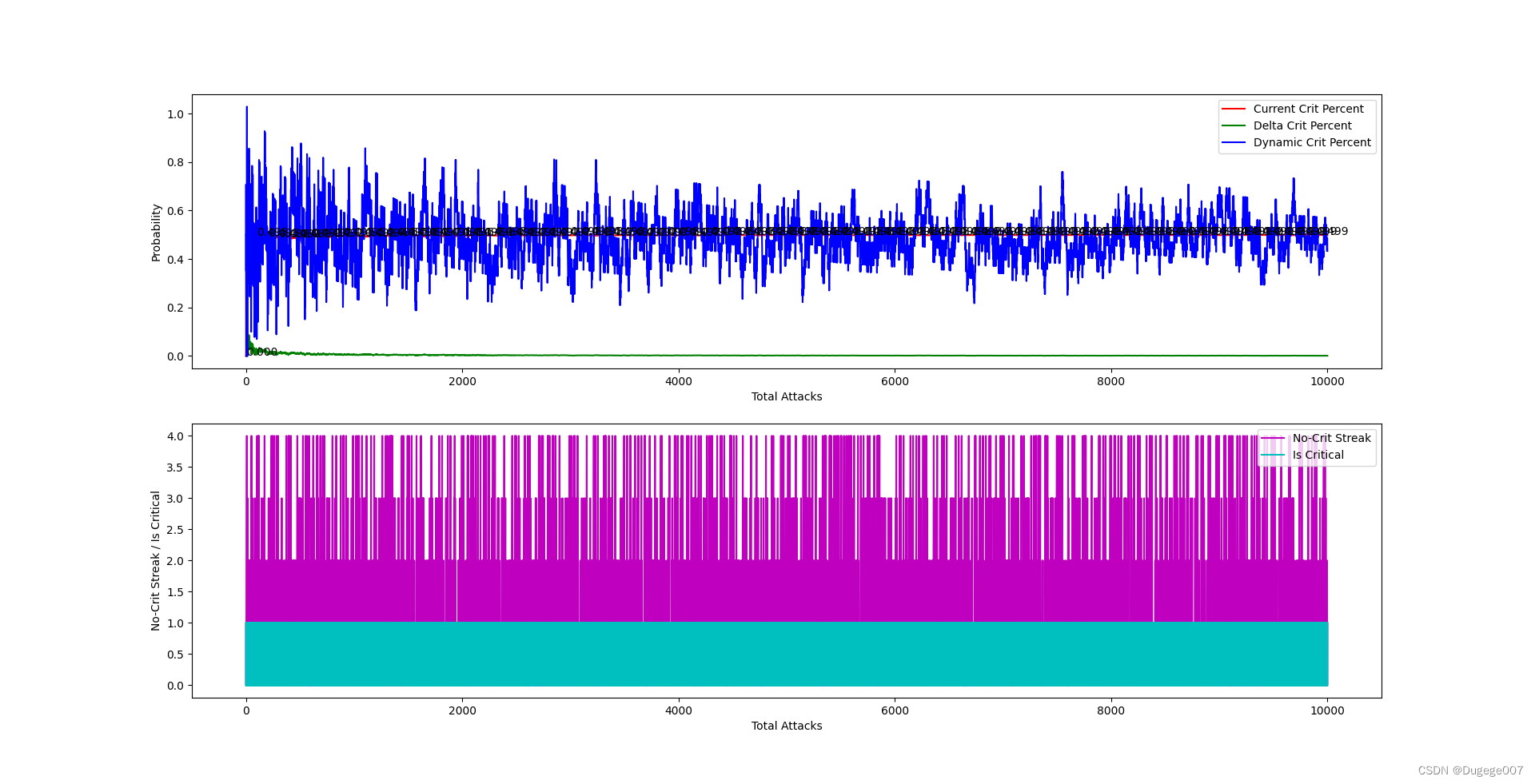
前 2000 次 如下
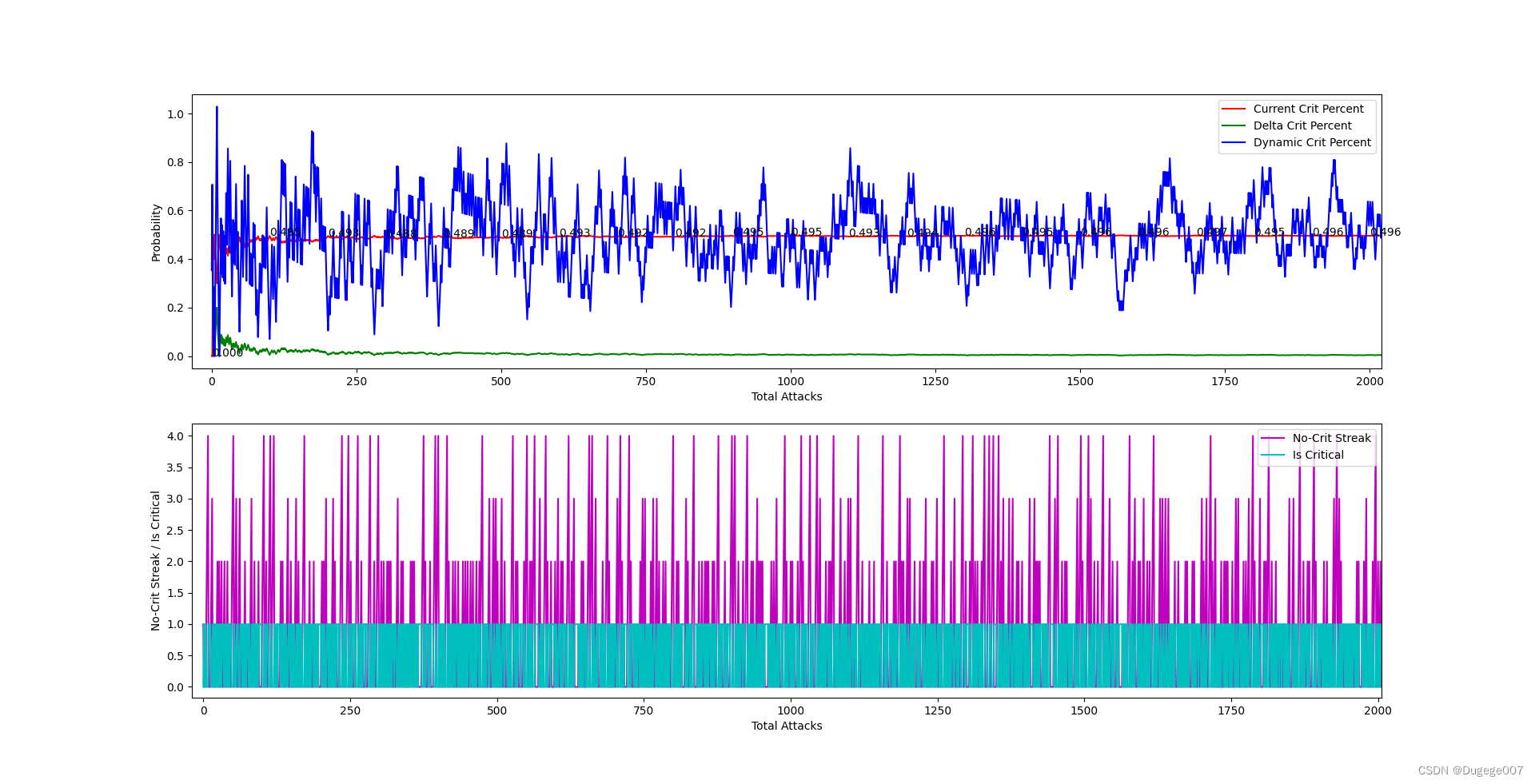
8000 ~ 10000 次 如下
也基本符合预期。
掷骰子
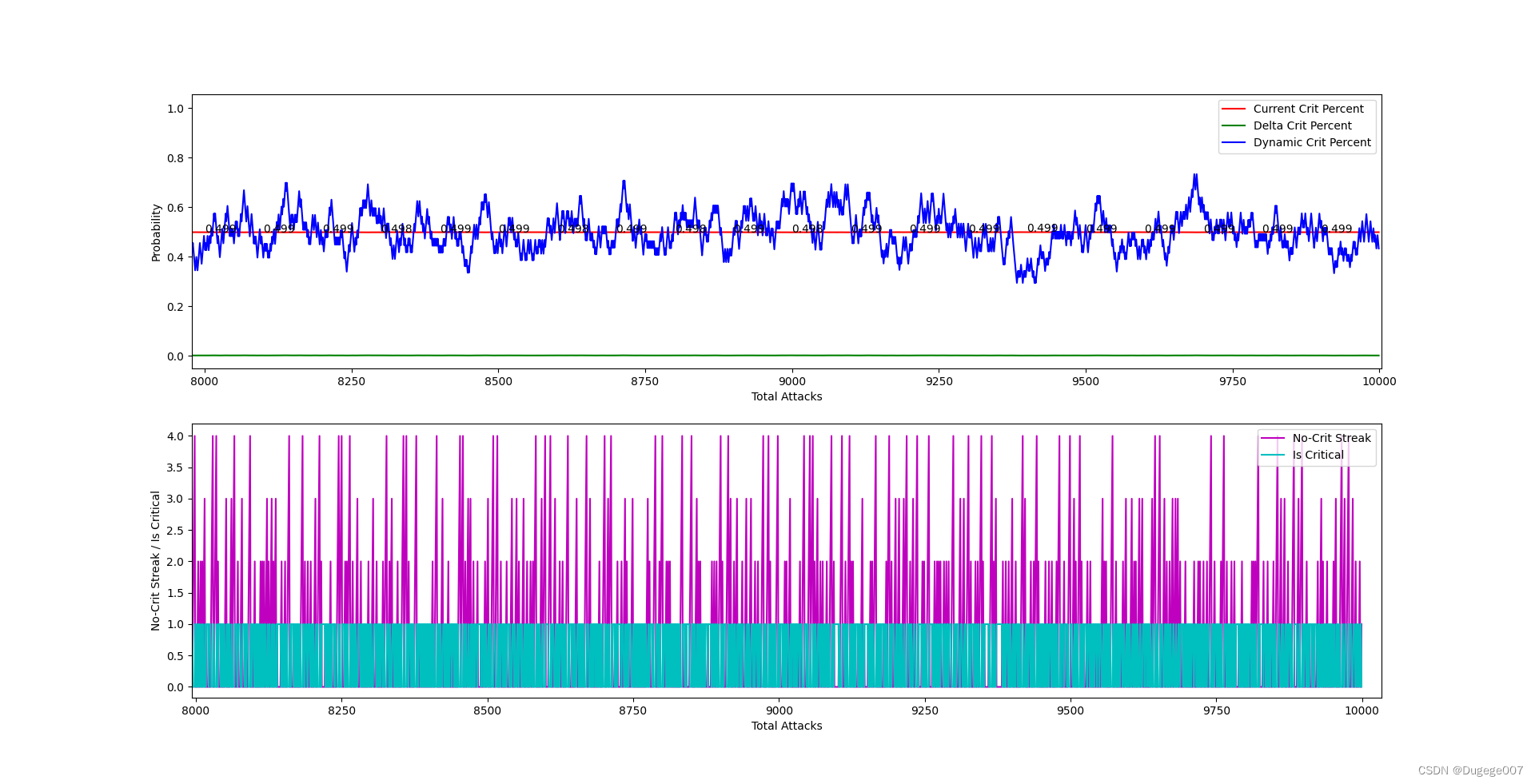
再以掷骰子为例:每掷出 15 次至少有一次是 点数 1。
# 同上文代码
InitCritPercent = 0.166667
dynamicCritPercent = 0.166667
# 同上文代码# 测试 10000 次
for i in range(10000):# 同上文代码# 检查是否连续 14 次未掷出正面if noCritStreakCount < 14:# 同上文代码# 同上文代码# 同上文代码
输出结果如下图所示
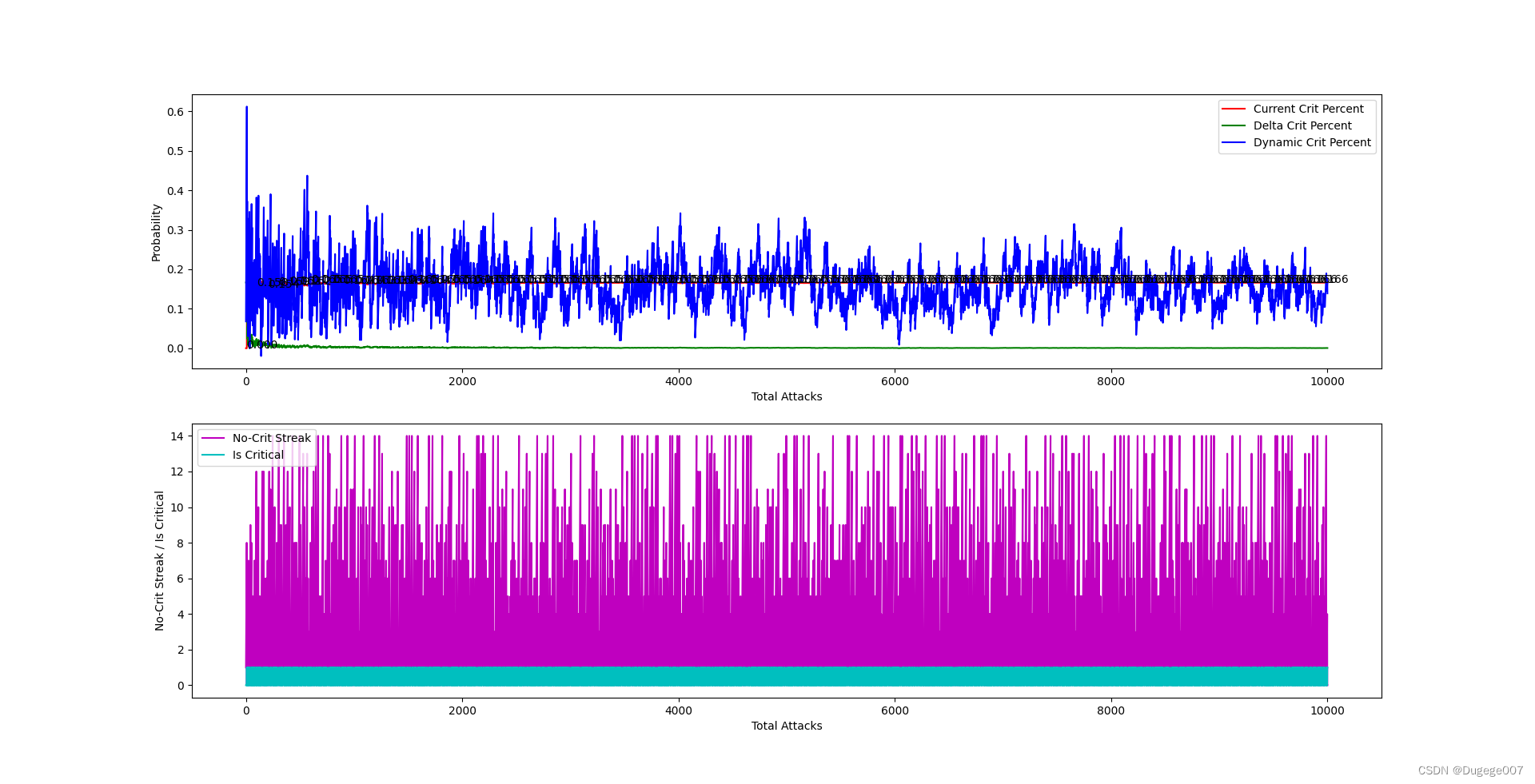
前 2000 次 如下
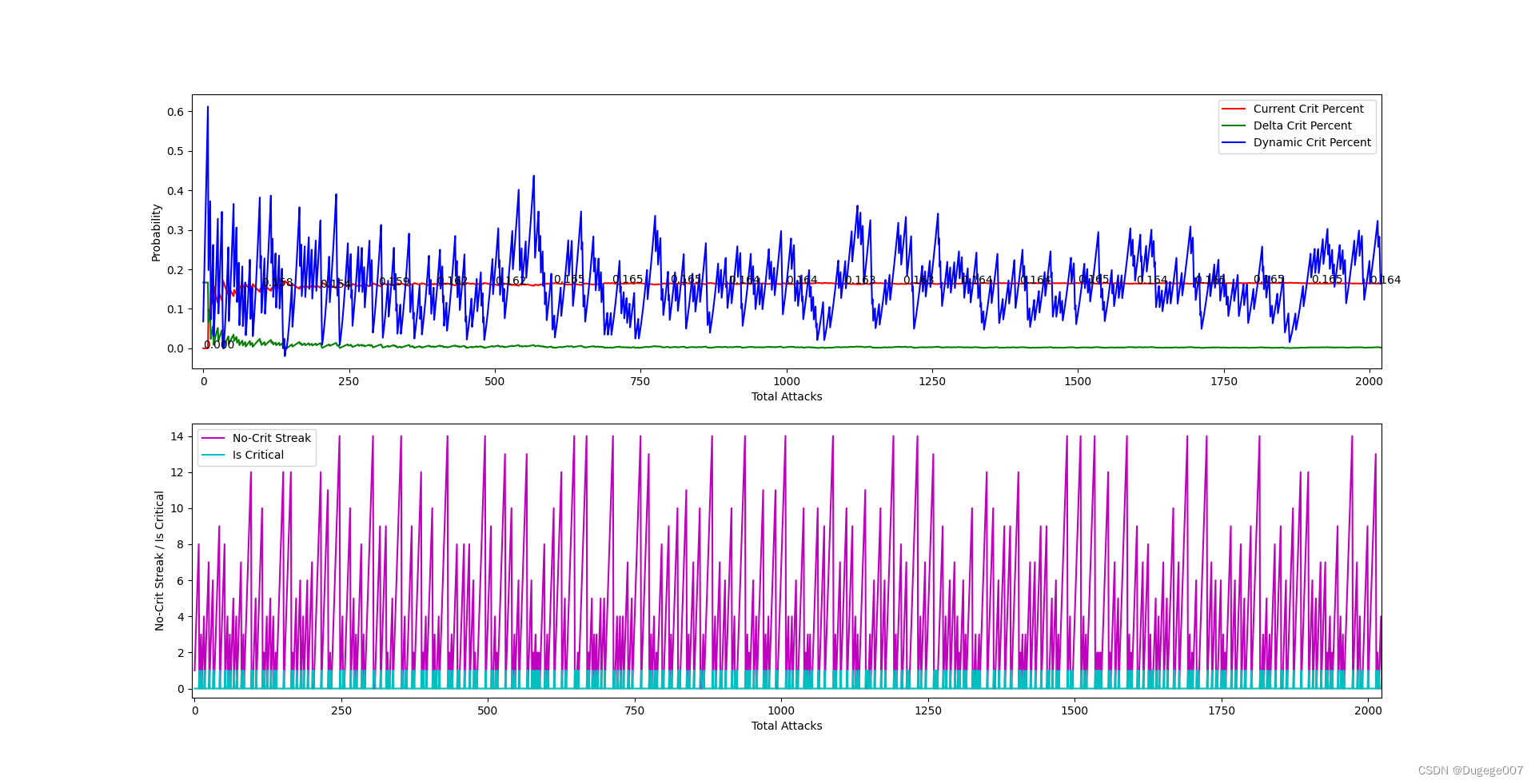
8000 ~ 10000 次 如下
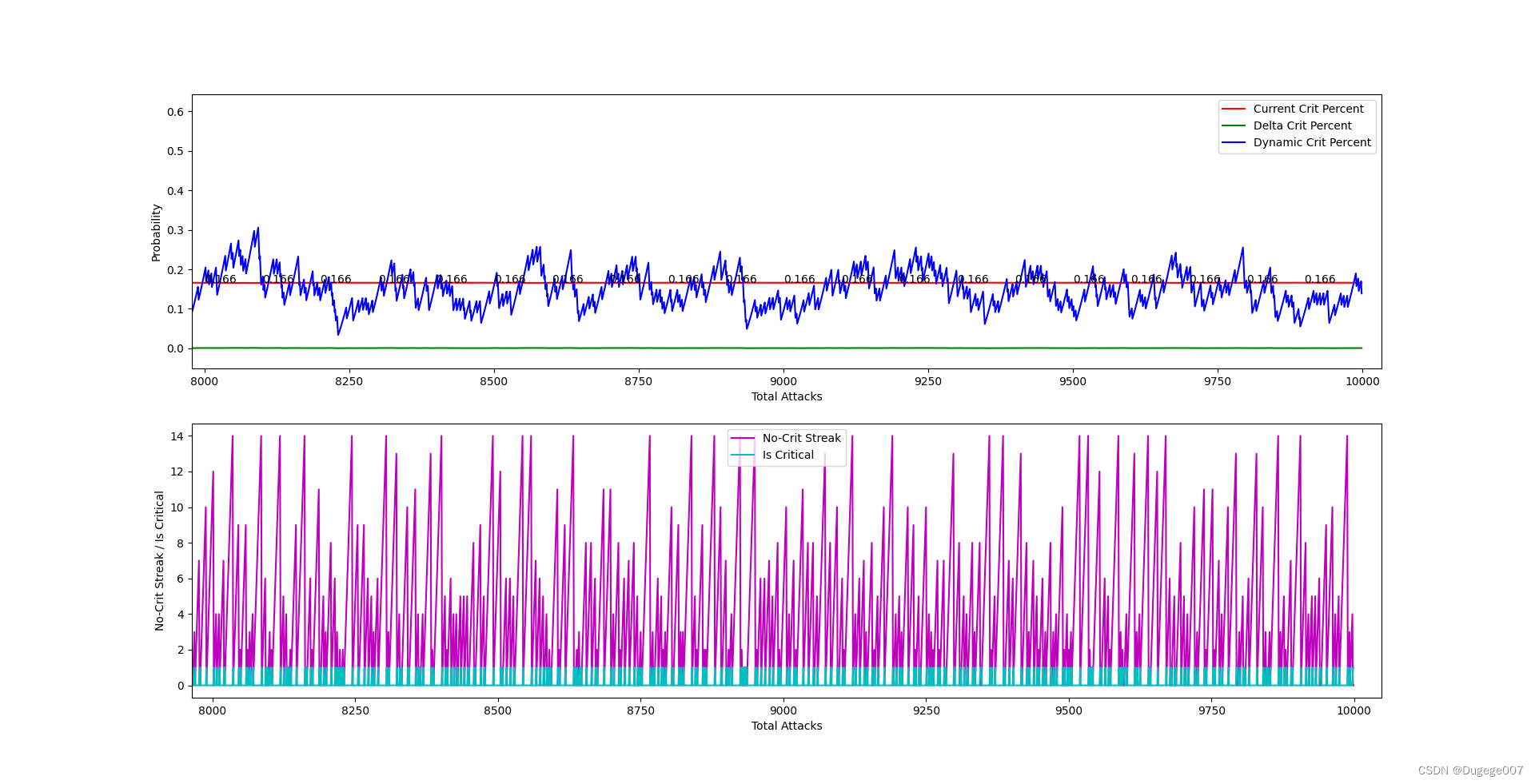
稳定发挥。
优化
目前“镜像修正”算法已经基本可用了,但是虽然叫“镜像”,却已经没有了镜像当初的样子。
不如就直接改名叫“动态平衡概率”算法好了…
算法优化
细心的朋友应该会发现,这套算法在一开始的概率会低于目标概率一些,并且逼近的速度还是慢了些。后期稳定性也没有想象中的高。
笔者目前能想到的继续优化的方式有三种:
1.分段修改 deltaCritPercent 的开根,类似LOD模型替换的感觉;
2.用 log 函数做系数,然后当次数达到一定值时直接 * deltaCritPercent 就可以了;
3.按目标概率的比例,给“总攻击次数”和“总暴击次数”设置较大的初始值。这样不用给 deltaCritPercent 开平方,就能得到一个较为满意的结果,也会相对高效一些。
笔者还没来得及测试性能,如果后续有相关优化会修改本文章,或者发一篇新文章。
关于判断次数
我们感觉到的小概率事件发生的概率通常在 5% 或 1% 以下,通过这两个标准,我们可以很轻松地得出“目标概率为 X 时,操作 N 次至少出现一次目标事件”中的N:
def find_optimal_N(p):# 从 1 到 500for i in range(1, 501):if(1 - p) ** i <= 0.05:return iprint(find_optimal_N(0.2))
print(find_optimal_N(0.5))
print(find_optimal_N(0.166667))# 输出结果为:
# 14
# 5
# 17
所以当目标概率为 0.2、0.5、0.166667 时,N 比较合适的值为 14、5、17。
当目标概率小于 0.05 时,可以让if(1 - p) ** i <= 0.01:,或者更小。
结语
虽然本算法目前还有待优化,但已经足够应对一些游戏场景。
关于那多出的2.5%的问题,笔者会继续探索,直到找到满意的答案。
如果这篇文章能为你解决问题或带来新的启发,那我会感到非常荣幸!
对于已经在这个领域有丰富经验的大佬们,非常欢迎你们的建议或批评。这不仅能帮助我改进,也能让这篇文章更加完善,从而帮助到更多的人。
感谢你抽出宝贵的时间来阅读这篇文章,如果你觉得有用,也请不吝分享给更多需要的人。
再次感谢,期待我们在知识的海洋里再次相遇!
相关文章:

游戏中的随机——“动态平衡概率”算法
前言 众所周知计算机模拟的随机是伪随机,但在结果看来依然和现实中的随机差别不大。 例如掷硬币,连续掷很多很多次之后,总有连续七八十来次同一个面朝上的情况出现,计算机中一般的随机函数也能很好模拟这一点。 但在游戏中&…...
)
AUTOSAR汽车电子嵌入式编程精讲300篇-基于 FIFO 和优先级序列 CAN 总线系统(续)
目录 4.1.2 理想模型的 FIFO 序列分析 4.2 仅有一个缓冲区的模型的可调度性分析...
C# InformativeDrawings 生成素描画
效果 项目 下载 可执行程序exe下载 源码下载...
)
关于网络协议的若干问题(一)
1、当网络包到达一个网关的时候,可以通过路由表得到下一个网关的 IP 地址,直接通过 IP 地址找就可以了,为什么还要通过本地的 MAC 地址呢? 答:IP报文端到端的传输过程中,在没有NAT情况下,目的地…...
电脑重做系统---win10
电脑重做系统---win10 前言制作启动U盘材料方法打开网址下载启动盘制作工具参照官方说明进行制作使用U盘重做系统 常用软件官网地址 前言 记得最早学习装电脑还是04年左右,最为一个啥也不知道的大一傻白胖,花了几百大洋在电脑版把了个“电脑组装与维修”…...

HTML基础入门02
目录 1.格式化标签 2.图片标签: img 3.超链接标签: a 4.综合案例: 展示博客2 5.表格标签 5.1基本使用 5.2合并单元格 6.列表标签 1.格式化标签 加粗:strong标签和b标签 倾斜:em标签和i标签 删除线:del标签和s标签 下划线:i…...

【C++】如何使用RapidXML读取和创建XML文件
2023年10月11日,周三下午 目录 RapidXML的官网使用rapidXML读取XML文件中的元素的属性和值此次要读取的XML文件:ReadExample.xml用于读取此XML文件的C代码运行结果使用rapidXML创建XML文件用于创建XML文件的C代码 如果上面的代码无法运行运行结果编辑…...

《UnityShader入门精要》学习3
笛卡尔坐标系(Cartesian Coordinate System) 二维笛卡儿坐标系 一个二维的笛卡儿坐标系包含了两个部分的信息: 一个特殊的位置,即原点,它是整个坐标系的中心。两条过原点的互相垂直的矢量,即x轴和y轴。这…...

使用Python将MP4视频转换为图像
介绍: 在计算机视觉和机器学习领域,我们经常需要处理视频数据。有时候,我们可能需要将视频转换为图像序列,以便进行后续的分析和处理。本文将介绍如何使用Python和OpenCV库将MP4视频文件转换为图像序列。 步骤: 导入…...

【Vue Router 3】入门
简介 Vue Router让SPA(Single-page Application)的构建更加容易。 Vue Router的功能: 嵌套的路由/视图映射模块化的、基于组件的router配置route params, query, wildcards由Vue过渡系统支持的视图过渡效果细粒度(fine-grained…...

SpringMVC中@RequestMapping注解的详细说明
RequestMapping 是Spring MVC中一个用于映射HTTP请求和控制器方法之间关系的注解。它用于定义控制器方法如何响应特定的HTTP请求,包括GET、POST、PUT、DELETE等。以下是RequestMapping注解的详细说明: 基本用法: RequestMapping("/examp…...

Java - 发送 HTTP 请求的及其简单的方法模块 - hutool
目录 一、POST 传递简单的字符串内容 .body(params)二、POST 传递 Json 数据,以表单类型传递 .form(params)二、POST 传递 Json 数据,以表单类型传递 .form(params) 和 .body(params) 方法效果等效的思路四、传统接口带 token 验证的代码模板参考链接 一…...

Nie et al. 2010 提出的不等式定理
这里写自定义目录标题 定理 定理 For any vector a a a and b b b, we have ∥ a ∥ 2 − ∥ a ∥ 2 2 2 ∥ b ∥ 2 ≤ ∥ b ∥ 2 − ∥ b ∥ 2 2 2 ∥ b ∥ 2 \|a\|_{2} - \frac{\|a\|_{2}^{2}}{2\|b\|_{2}} \leq \|b\|_{2} - \frac{\|b\|_{2}^{2}}{2\|b\|_{2}} ∥a∥2−…...

chatGLM2-6B模型LoRA微调数据集实现大模型的分类任务
【TOC】 1.chatglm介绍 ChatGLM 模型是由清华大学开源的、支持中英双语问答的对话语言模型,并针对中文进行了优化。该模型基于 General Language Model(GLM)架构,具有 62 亿参数。结合模型量化技术,用户可以在消费级的显卡上进行本地部署。 ChatGLM 具备以下特点: 充…...

Elasticsearch6实践
目录 目录 一、需求 二、ES索引设计 三、页面搜索条件 四、ES的分页搜索DSL语句 五、其他 一、需求 公告列表,需要支持以下搜索 1、根据文本输入,模糊搜索公告标题和公告正文。 2、支持公告类型搜索,单选 3、支持根据公告所在省市区搜…...
云原生Kubernetes:K8S集群版本升级(v1.20.6 - v1.20.15)
目录 一、理论 1.K8S集群升级 2.集群概况 3.升级集群 4.验证集群 二、实验 1.升级集群 2.验证集群 三、问题 1.给node1节点打污点报错 一、理论 1.K8S集群升级 (1)概念 搭建K8S集群的方式有很多种,比如二进制,kubeadm…...

毅速丨3D打印随形水路模具日常如何保养
3D打印随形水路的蜿蜒曲折甚至细微水路,使得其容易发生堵塞并难以清洗,一旦堵塞将对生产带来不小的影响。事实上,堵塞的发生是逐步发展的,所以在生产过程中应注意监控,一旦发现冷却效果下降应及时检查。以下是一些防患…...
尚品甄选2023全新SpringBoot+SpringCloud企业级微服务项目
最适合新手入门的SpringBootSpringCloud企业级微服务项目来啦!如果你已经学习了Java基础、SSM框架、SpringBoot、SpringCloud,想找一个项目来实战练习;或者你刚刚入行,需要可以写到简历中的微服务架构项目! 项目采用前…...
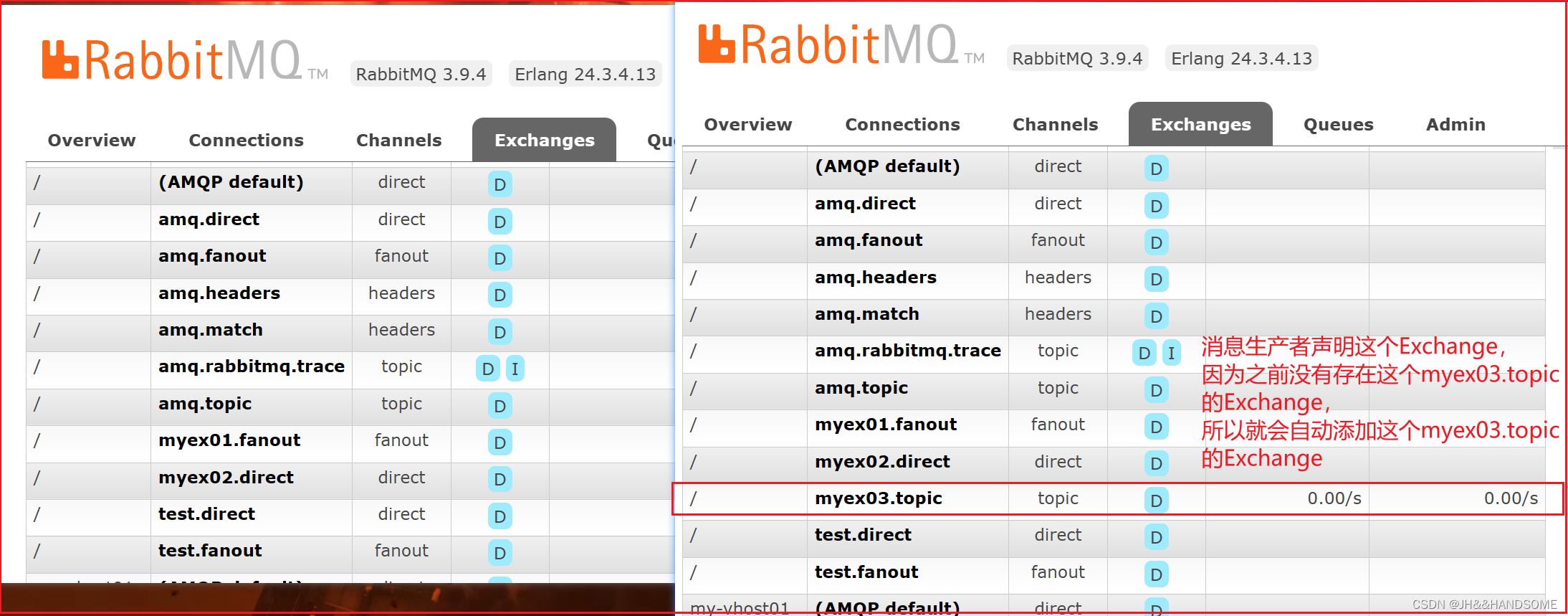
204、RabbitMQ 之 使用 topic 类型的 Exchange 实现通配符路由
目录 ★ 使用topic实现通配符路由代码演示topic通配符类型的Exchange代码演示:ConstantUtilConnectionUtilProducerConsumer01执行结果生产者消费者01消费者02 完整代码:ConstantUtilConnectionUtilProducerConsumer01Consumer02pom.xml ★ 使用topic实现通配符路由…...
qq视频录制教程,让你的视频更加精彩
“qq视频可以录制吗?浏览qq的时候发现一段有趣的视频,点击下载却一直显示失败,朋友叫我把视频录制下来,但是我不知道怎么操作,想问问大家,有没有办法录制qq的视频。” 在信息化的时代,通过视频…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
