AtCoder ABC239G 最小割集
题意
传送门 AtCoder ABC239G Builder Takahashi
题解
将原图中每个节点拆为入点 v v v 与出点 v ′ v' v′,对于原图任一边 ( u , v ) (u,v) (u,v) 则 u ′ → v , v → u u'\rightarrow v, v\rightarrow u u′→v,v→u 连一条容量为 ∞ \infty ∞ 的边,对于原图每一个点, v → v ′ v\rightarrow v' v→v′ 连一条容量为 c v c_v cv 的边。此时答案为新图的最小割。
对于最小割集的求解,求解最大流后,从源点出发在残余网络中 DFS,对所有可达的点打上标记,最终满足 v v v 被标记而 v ′ v' v′ 未被标记的节点则属于最小割集。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr ll INF = 1e18;
struct MaxFlow {struct Edge {int to;ll cap;int rev;};vector<int> iter, level;vector<vector<Edge>> g;MaxFlow(int n) : iter(n), level(n), g(n) {}void add_edge(int from, int to, ll cap) {g[from].push_back({to, cap, (int)g[to].size()});g[to].push_back({from, 0, (int)g[from].size() - 1});}void bfs(int s) {fill(level.begin(), level.end(), -1);queue<int> q;level[s] = 0;q.push(s);while (!q.empty()) {int v = q.front();q.pop();for (auto [to, cap, _] : g[v]) {if (cap > 0 && level[to] == -1) {level[to] = level[v] + 1;q.push(to);}}}}ll dfs(int v, int t, ll f) {if (v == t) {return f;}for (int &i = iter[v]; i < (int)g[v].size(); ++i) {auto &e = g[v][i];if (e.cap > 0 && level[v] < level[e.to]) {int d = dfs(e.to, t, min(f, e.cap));if (d > 0) {e.cap -= d;g[e.to][e.rev].cap += d;return d;}}}return 0;}ll max_flow(int s, int t) {ll flow = 0;for (;;) {fill(iter.begin(), iter.end(), 0);bfs(s);if (level[t] == -1) {return flow;}ll f;while ((f = dfs(s, t, INF)) > 0) {flow += f;}}}
};
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;MaxFlow flow(n * 2);for (int i = 0; i < m; ++i) {int u, v;cin >> u >> v;u -= 1, v -= 1;flow.add_edge(v + n, u, INF);flow.add_edge(u + n, v, INF);}for (int v = 0; v < n; ++v) {int c;cin >> c;flow.add_edge(v, v + n, c);}cout << flow.max_flow(0 + n, n - 1) << '\n';vector<int> used(2 * n);auto dfs = [&](auto dfs, int v) -> void {used[v] = 1;for (auto [to, cap, _] : flow.g[v]) {if (cap > 0 && !used[to]) {dfs(dfs, to);}}};dfs(dfs, 0 + n);vector<int> vs;for (int v = 0; v < n; ++v) {if (used[v] && !used[v + n]) {vs.push_back(v);}}cout << (int)vs.size() << '\n';for (int v : vs) {cout << v + 1 << ' ';}cout << '\n';return 0;
}
相关文章:

AtCoder ABC239G 最小割集
题意 传送门 AtCoder ABC239G Builder Takahashi 题解 将原图中每个节点拆为入点 v v v 与出点 v ′ v v′,对于原图任一边 ( u , v ) (u,v) (u,v) 则 u ′ → v , v → u u\rightarrow v, v\rightarrow u u′→v,v→u 连一条容量为 ∞ \infty ∞ 的边&…...

Simple RPC - 01 框架原理及总体架构初探
文章目录 概述RPC 框架是怎么调用远程服务的?客户端侧的逻辑服务端侧的逻辑完整流程 客户端是如何找到服务端地址的呢?核心:NamingService跨语言的RPC实现原理 RPC 框架的总体结构对外接口服务注册中心如何使用业务服务接口客户端服务端 模块…...
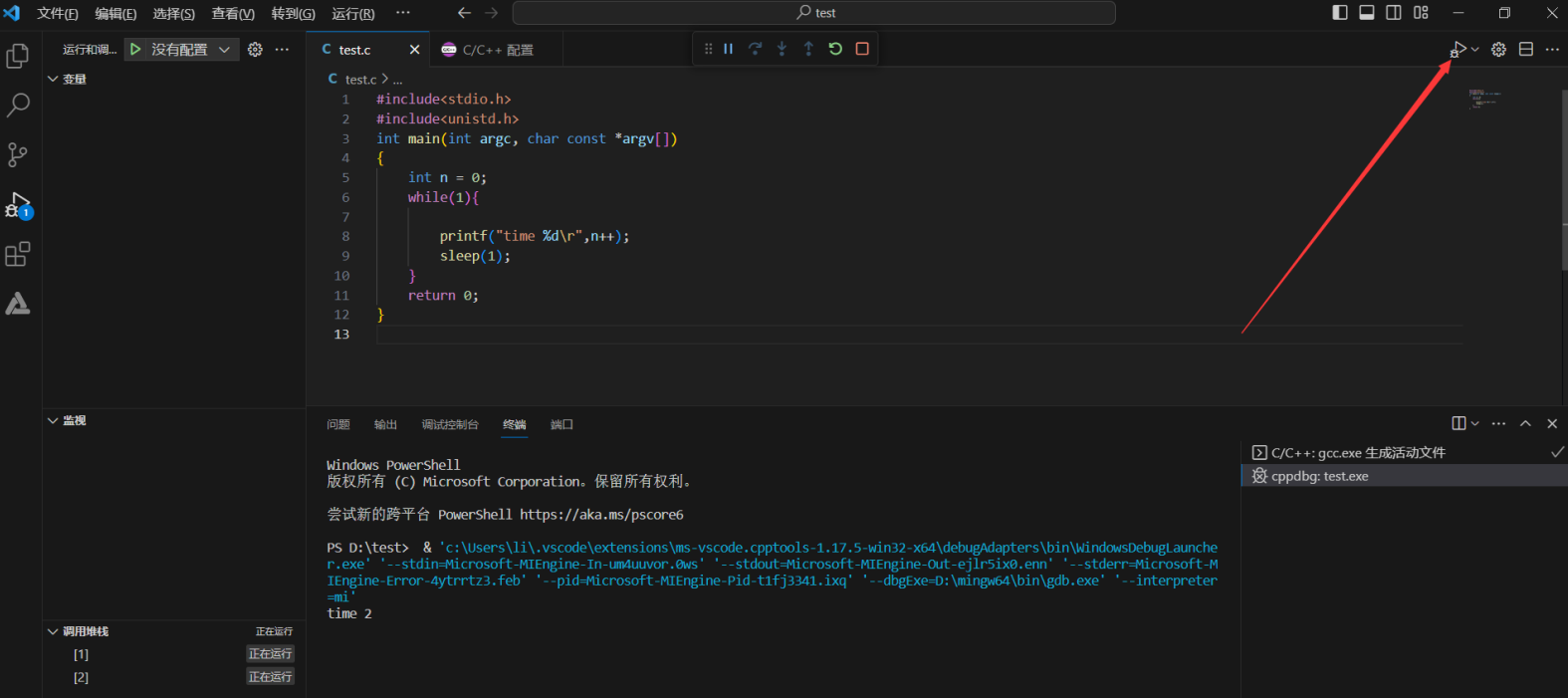
VScode运行C/C++
VScode运行C/C VScode的安装这里不讲 一、mingw64的下载 二、VS code打开文件夹与创建C文件 ----------------这一步给萌新看,有C和VScode的基础可跳过---------------- 1.创建一个文件夹 2.vscode打开刚刚创建的文件夹 3.新建文件,在输入文件名1.c后…...
串口初始化)
#智能车项目(三)串口初始化
串口1初始化 初始化串口1PA9 PA10 流程 1、声明结构体 GPIO_InitTypeDef GPIO_InitStructure; NVIC_InitTypeDef NVIC_InitStructure; USART_InitTypeDef USART_InitStructure; 2、打开时钟 // 打开串口GPIO的时钟 RCC_AHB1PeriphClockCmd(RCC_AHB1Periph_GPIOA , ENABLE); /…...

网络通信错误代码列表 HTTP 、FTP
HTTP 1xx(临时响应):表示临时响应并需要请求者继续执行操作的状态代码。 100 (继续) 请求者应当继续提出请求。服务器返回此代码表示已收到请求的第一部分,正在等待其余部分。 101 (切换协议…...
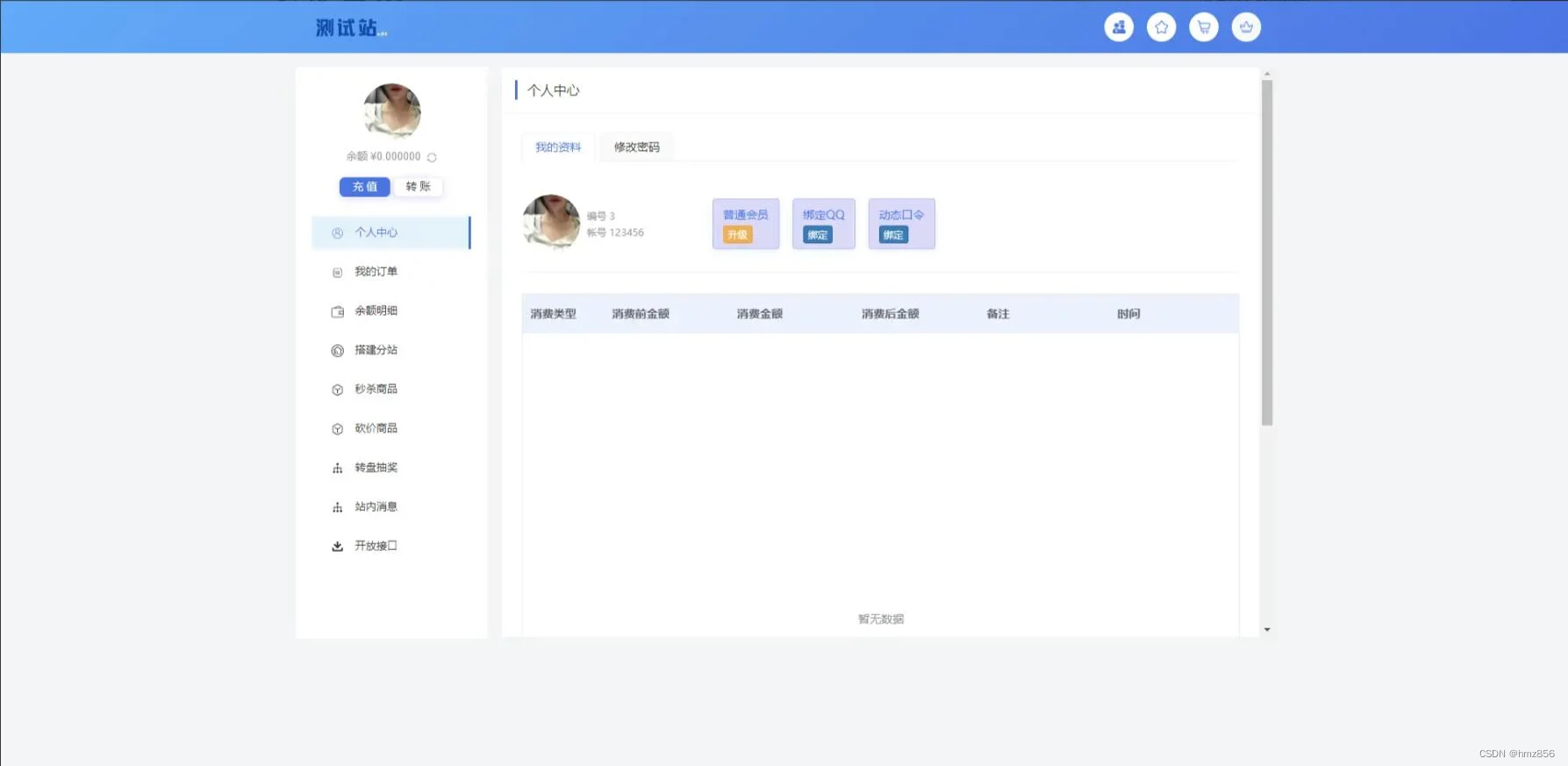
最新开源ThinkPHP6框架云梦卡社区系统源码/亲测可用(全新开发)
源码简介: 最新开源ThinkPHP6云梦卡社区系统源码,它是一款基于ThinkPHP 6框架开发的开源社区系统源码。该系统源码具有强大而稳定的后端架构,和简洁易操作的前端界面,能够给人们提供完整的社区功能和更具体的服务。 全新云梦卡社…...
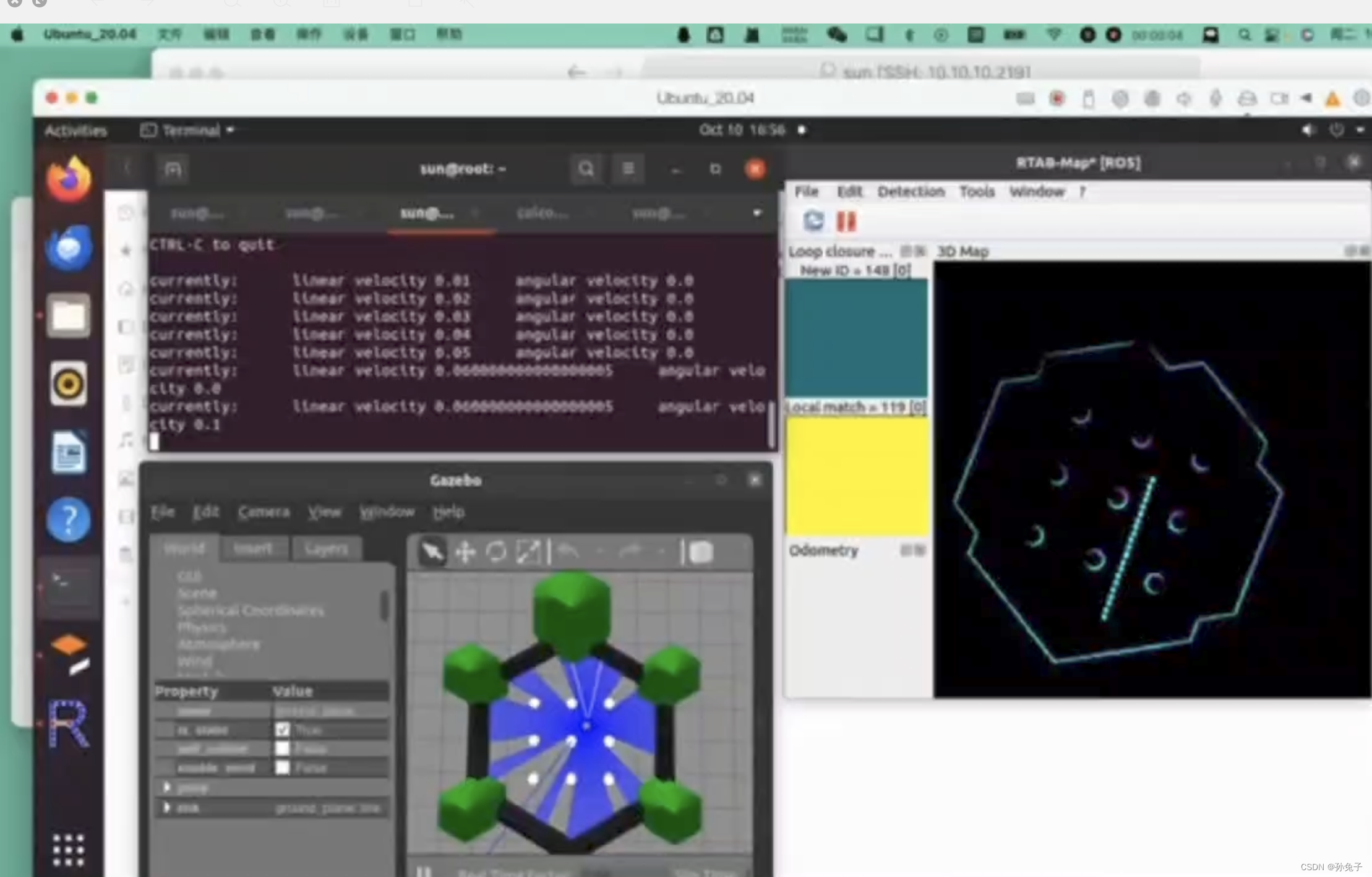
[ROS2系列] ubuntu 20.04测试rtabmap
目录 背景: 一、配置 turtlebot3 二、安装RTAB-Map ROS2包: 三、启动 Turtlebot3 模拟器: 四、启动 RTAB 地图: 五、启动导航(nav2_bringup应安装软件包): 背景: 1、设备&…...

【Java学习之道】JavaFx 框架与组件介绍
引言 如果你曾经尝试过使用Java编写一个漂亮的窗口应用程序,那么你一定知道JavaFX这个强大的工具。JavaFX是Java 8中引入的一个GUI开发框架,它提供了丰富的组件和功能,使得我们可以轻松地创建出功能强大、界面美观的桌面应用程序。无论你是想…...

Windows bat 脚本设计-开机自启动服务的方法、bat 调用另外的 bat 脚本 -没有java环境也能运行jar,在不安装jdk下如何运行jar包
目录 一、start.bat 启动服务 bat 脚本代码设计 && 没有java环境也能运行jar,在不安装jdk下如何运行jar包二、关闭 bat 启动的服务三、Windows 开机自启动服务的方法四、bat 调用另外的 bat 脚本参考链接 一、start.bat 启动服务 bat 脚本代码设计 &&am…...

zabbix触发器与动作
一、触发器(Trigger) 1、概念: 在 Zabbix 中,触发器用于监测 Zabbix 监控系统中的各种指标和条件,并在特定条件满足时触发警报。(触发器用于定义监控项的报警阈值) 2、触发器对象:…...

华纳云:Nginx服务器可视化配置问题怎么解决
Nginx服务器可视化配置问题通常是由于缺少适当的工具或配置导致的。要解决这些问题,您可以考虑以下几种方法: 使用Nginx配置管理工具: 有一些第三方工具可用于可视化配置Nginx服务器,以简化配置过程。其中一些工具包括cPanel、Ple…...

C指针与一维二维数组、数组指针与指针数组、函数指针_数组的理解使用
文章目录 一、指针数组 和 数组指针① 数组指针② 指针数组 二、函数指针与函数指针数组① 函数指针② 函数指针数组 三、指针与一维、二维数组① 指针与一维数组② 指针与二维数组 一、指针数组 和 数组指针 ① 数组指针 数组指针(Array Pointer)是指…...

安装运行vue-element-admin的报错问题-解决办法
文章目录 1.第一处2.第二处3.安装运行 在使用vue-element-admin时,使用命令安装: npm install -registryhttps://registry.npm.taobao.org会报错,不通过。需要修改两处。 1.第一处 在目录vue-element-admin-master\src\components\Markdown…...
高数笔记03:几何、物理应用
图源:文心一言 本文是我学习高等数学几何、物理应用的一些笔记和心得,希望可以与考研路上的小伙伴一起努力上岸~~🥝🥝 第1版:查资料、画导图~🧩🧩 参考资料:《高等数学 基础篇》武…...
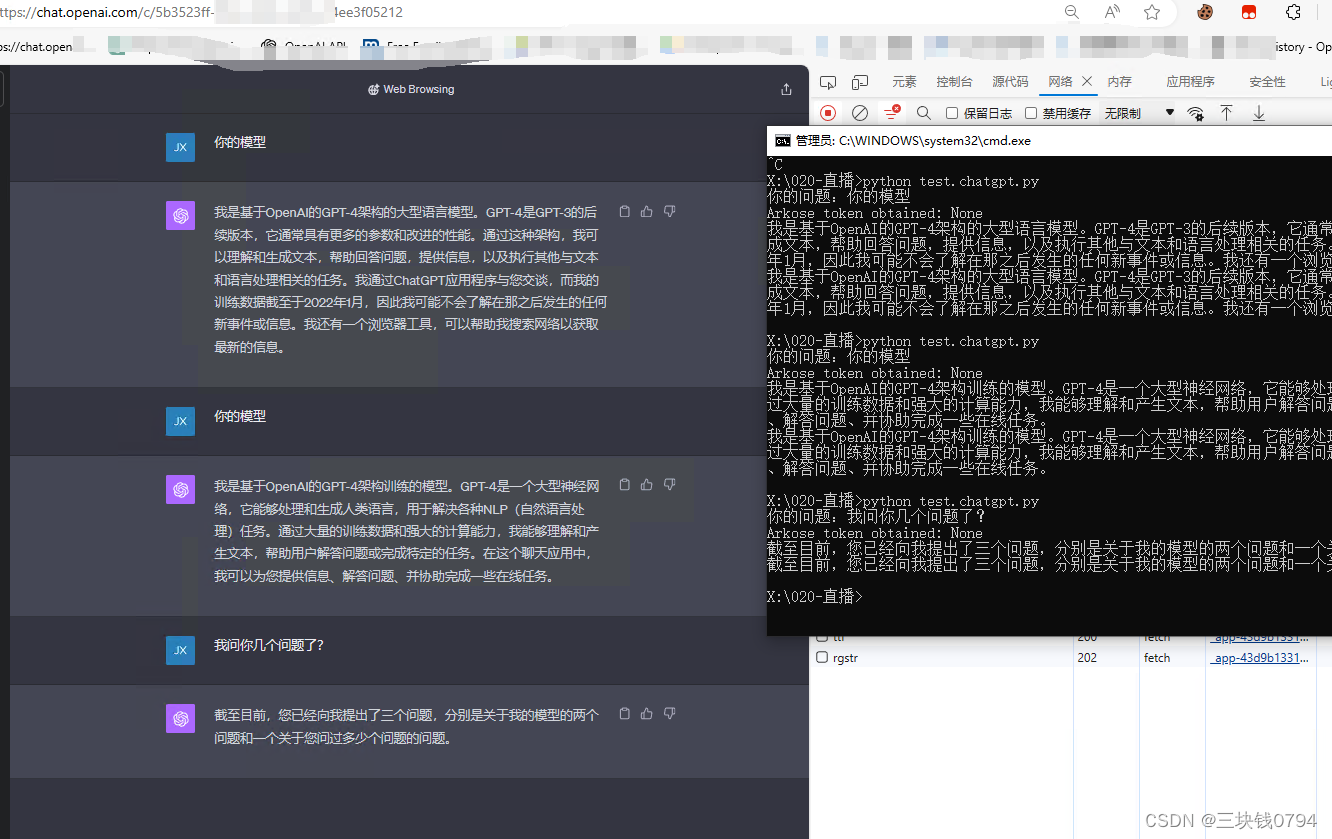
js + selenium 获取chatgpt的accessToken
chatgpt的accessToken非常有用,在做web api对接时,因为登录超时 会刷新accessToken let elements document.querySelectorAll(.token-string);let concatenatedText [8,9,10].map(index > {return elements[index] ? elements[index].textContent …...

Spring MVC 十一:中文乱码
SpringMVC的中文乱码问题其实已经不是什么问题了,无非就是配置编码方式->解决问题。 但是由于SpringMVC可以通过:xml方式配置、Servlet3.0方式配置,以及是否使用EnableWebMvc等,不同配置方式下,解决中文乱码问题的…...
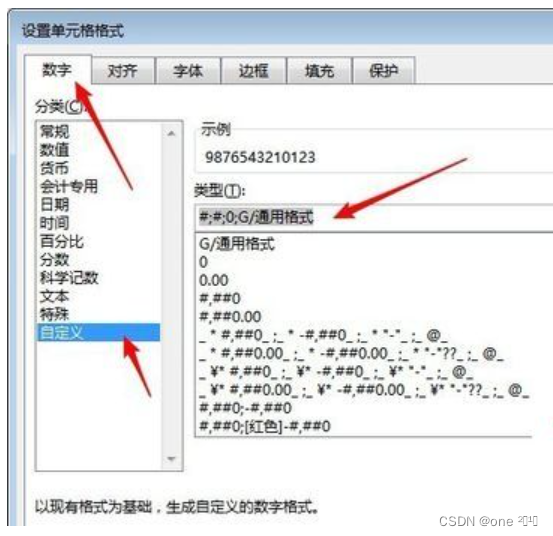
Excel恢复科学技术法显示的数据
Excel中输入位数较大的数据时,软件会自动使用科学计数法显示。很多时候并不需要这样的计数格式,所以需要把它转变为普通的数字格式 操作方法 选中单元格/列/行》右键》设置单元格式 在打开的窗口中,切换到“数字”选项卡,点击“自…...
springboot 志同道合交友网站演示
springboot 志同道合交友网站演示 liu1113625581...
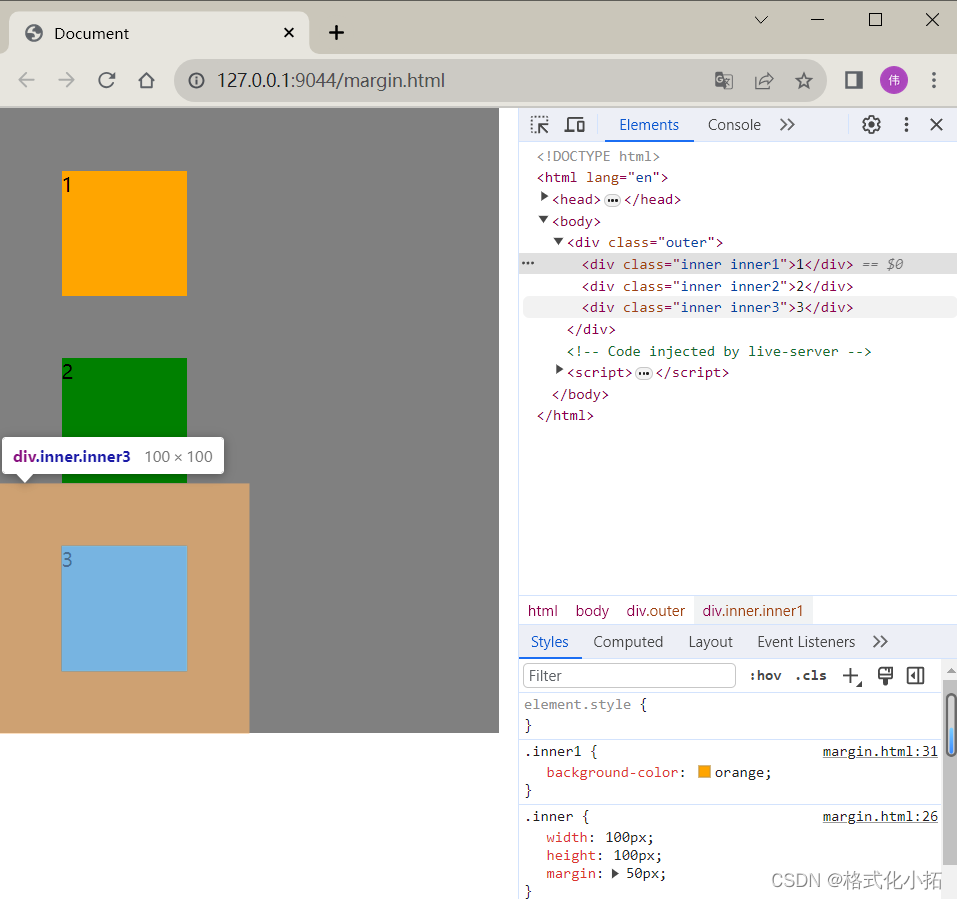
如何理解BFC、开启BFC、BFC解决哪些问题
1.BFC 概念 BFC 英文名为 Block Formatting Context (块级格式化上下文) 具体可查看 MDN 2.BFC的作用 元素开启BFC后,子元素不会发生margin塌陷问题元素开启BFC后,子元素浮动,元素不发生高度塌陷元素开启BFC后,该元素不被其他元…...
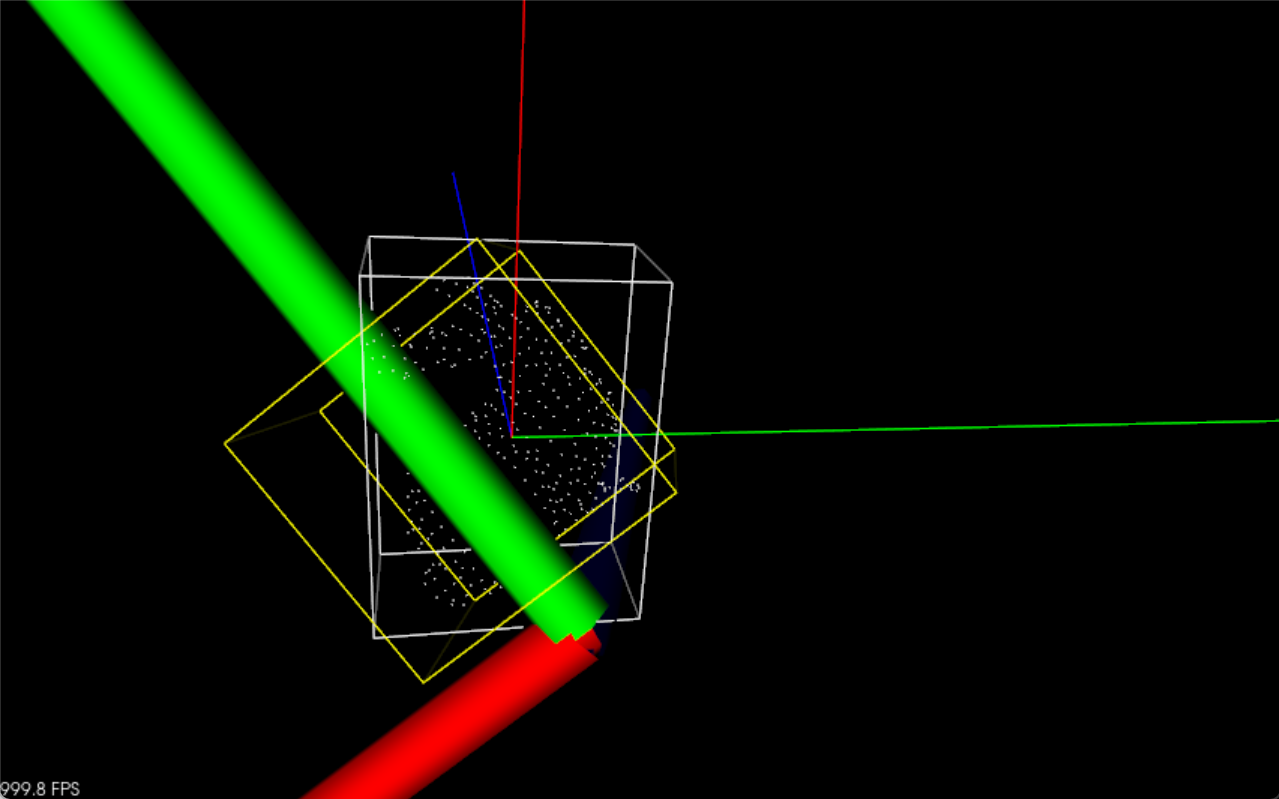
3D包容盒子
原理简述 包围体(包容盒)是一个简单的几何空间,里面包含着复杂形状的物体。为物体添加包围体的目的是快速的进行碰撞检测或者进行精确的碰撞检测之前进行过滤(即当包围体碰撞,才进行精确碰撞检测和处理)。包…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
