按字典序排列的最小的等价字符串[拆解并查集]
并查集
- 前言
- 一、按字典序排列的最小的等价字符串
- 二、并查集
- 总结
- 参考文献
前言
并查集有什么用?并查集是什么?搞懂这两个问题,相关的并查集问题就变得非常easy!
一、按字典序排列的最小的等价字符串

二、并查集
有一种方法,并查集,它能将有关系的东西归为一类。
这里的问题,根据两字符的等价关系,将其归为一类,并得到最小字典序的root字符。
这里是一样的,只是选择每类的root字符时,需要比较一下,取字典序最小的字符节点作为root。
idea)构建好并查集后,遍历字符串baseStr,通过并查集寻找该字符的root,即该类最小等价字符。
注:
并查集是什么?并查集 = 数组 + union操作,经典的 数据结构 + 算法 == 程序,数组中每个元素为一个节点,根据节点的关系进行union操作,将各个节点分类。
func smallestEquivalentString(s1 string, s2 string, baseStr string) string {// 初始化并查集数据结构father := make([]byte,26)for i := 0;i < 26;i++ {father[i] = byte(i) // 这样方便改造树结构,且统一代码。i == father[i],此时返回father[i]和i的效果是一样的。}// 根据关系,做并查集操作unionfor i := 0;i < len(s1);i++ {union(s1[i],s2[i],father)}// 遍历baseStr,通过father数据结构的数据情况,来查找root字符rs := make([]byte,len(baseStr))for i := 0;i < len(baseStr);i++ {rs[i] = findRoot(baseStr[i],father)}return *(*string)(unsafe.Pointer(&rs))
}
func union(c1,c2 byte,father []byte) {cr1 := findFather(c1 - 97,father)cr2 := findFather(c2 - 97,father)if cr1 != cr2 {if cr1 < cr2 {father[cr2] = cr1}else {father[cr1] = cr2}}
}
func findFather(c byte,father []byte) byte {// 寻rootif father[c] != c {father[c] = findFather(father[c],father)}return father[c]
}
func findRoot(ch byte,father []byte) byte {ch = ch - 97for ; father[ch] != ch; {ch = father[ch]}return ch + 97
}
总结
1)并查集是什么?程序 = 数据结构+算法,并查集程序 = 数组 + union联合两节点。
2)并查集有什么用?每个数组元素为一个节点,根据节点关系union两节点,所以并查集的作用就是将元素归类。
3)并查集就像树一样,但是不是用链表来实现父子节点,而是连续内存的数组来实现。这跟字典树用arraylist来实现类似,并查集是子节点存父节点在数组中的位置,字典树是父节点存各个子节点在数组中的位置。毕竟并查集是从子找父,而字典树是从父找子。
参考文献
[1] LeetCode 按字典序排列的最小等价字符串
相关文章:

按字典序排列的最小的等价字符串[拆解并查集]
并查集前言一、按字典序排列的最小的等价字符串二、并查集总结参考文献前言 并查集有什么用?并查集是什么?搞懂这两个问题,相关的并查集问题就变得非常easy! 一、按字典序排列的最小的等价字符串 二、并查集 有一种方法&#x…...

操作系统——6.系统调用
目录 1.概述 2.系统调用的定义和作用 2.1 定义 2.2 功能 2.3 分类 3.系统调用和库函数的区别 4.系统调用背后的过程 5.小结 1.概述 这篇文章我们主要来介绍一下操作系统中的系统调用,下面来看一下具体的框架图: 2.系统调用的定义和作用 2.1 定…...

JavaScript DOM操作
目录 获取元素: 修改元素属性: 添加、删除、替换元素: 修改样式: DOM(文档对象模型)是一种用于操作 HTML 和 XML 文档的 API。JavaScript 通过 DOM API 可以访问和操作页面中的元素、属性和样式等。 获…...

【数据结构】顺序表
文章目录前言初始化顺序表打印顺序表检查容量判空顺序表数据个数尾部插入尾部删除头部插入头部删除在pos位置插入数据删除pos位置的数据查找数据修改数据销毁顺序表整体代码写在最后前言 顺序表作为数据结构中的小小弟,还是很好应付的。说到数据结构,顺序…...

【人工智能 AI 】RPA 架构师需要具备的技能有哪些?RPA Solution Architect
RPA 架构师需要具备的技能有哪些?使用markdown格式,不少于3000字,细化到3级目录。 文章目录 一、RPA架构师需要具备的技能1. 对RPA的理解2. 对RPA技术的熟练掌握2.1 RPA系统的架构模式2.2 RPA软件的操作模式2.3 RPA程序的编写方式3. 对RPA应用的知识4. 对软件开发的基本知识…...
【模拟集成电路】鉴频鉴相器设计(Phase Frequency Detector,PFD)
鉴频鉴相器设计(Phase Frequency Detector,PFD)前言一、 PFD的工作原理二、 PFD电路设计(1)PFD电路图(2)D触发器电路图(3)与非门(NAND)电路图&…...
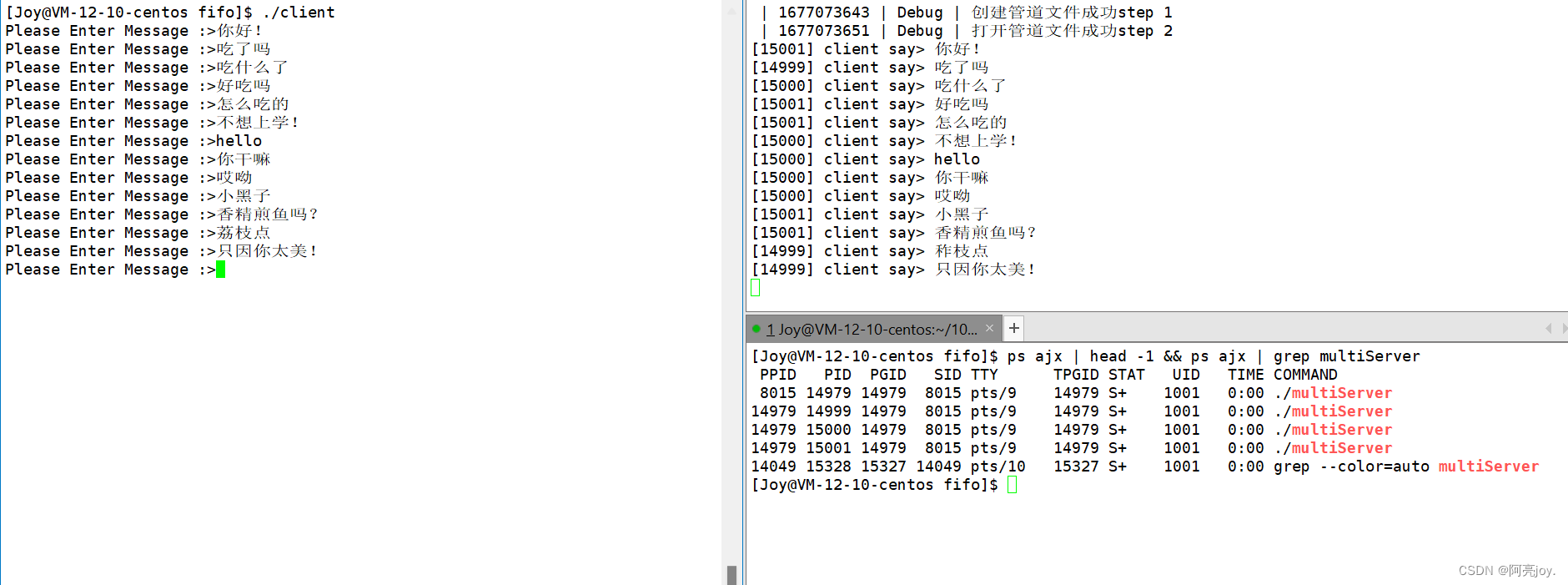
【Linux】进程间通信介绍 | 管道
🌠 作者:阿亮joy. 🎆专栏:《学会Linux》 🎇 座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录👉进程间通信…...

这次说说腾讯的一场 35K—55K 的 Android 高工面试
一、面试的由来 事情是这样的,因为跟公司发展一些想法的不同,早在十月份的时候就有了跳槽的想法,但是碍于老大的面子就一直就没有跟人事说出口,打算着等到年后金三银四在试试跳槽。 但是发生一件事终于让我忍不住了,…...
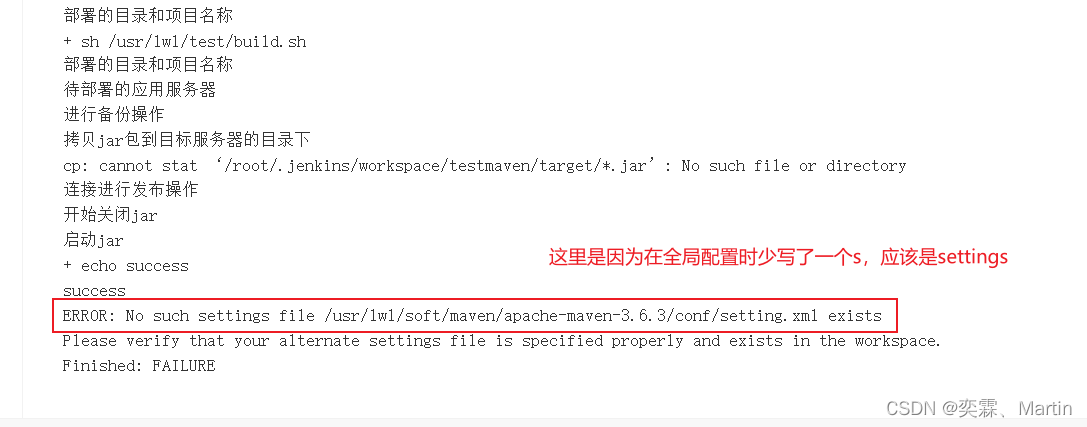
Jenkins第一讲
目录 一、Jenkins 1.1 敏捷开发与持续集成 1.1.1 敏捷开发 1.1.2 持续集成 1.2 持续集成工具 1.2.1 jenkins和hudson 1.2.2 技术组合 1.2.3 部署方式对比 1.3 安装Jenkins 1.3.1 下载Jenkins的war包 1.3.2 开启Jenkins 1.4 Jenkins全局安全配置 1.5 使用Jenkins部…...

变分推断 | MATLAB实现VBMC变分贝叶斯蒙特卡洛模拟的贝叶斯推断
变分推断 | MATLAB实现变分贝叶斯蒙特卡洛模拟的贝叶斯推断 目录 变分推断 | MATLAB实现变分贝叶斯蒙特卡洛模拟的贝叶斯推断效果一览基本介绍研究内容模型描述模型设计参考资料效果一览 基本介绍 MATLAB实现变分贝叶斯蒙特卡洛模拟的贝叶斯推断。变分贝叶斯蒙特卡洛(VBMC)是…...

代码随想录【Day25】| 216. 组合总和 III、17. 电话号码的字母组合
216. 组合总和 III 题目链接 题目描述: 找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。 说明: 所有数字都是正整数。 解集不能包含重复的组合。 示例 1: 输入: k 3, n 7 输…...
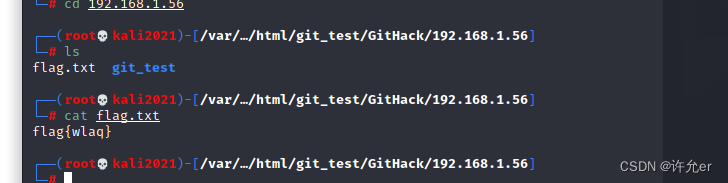
web中git漏洞的形成的原理及使用
目录 1.Git漏洞的成因 1.不正确的权限设置: 2.代码注入漏洞: 3.未经身份验证的访问: 4.非安全传输: 5.跨站脚本攻击(XSS): 2.git泄露环境的搭建 git init: git add࿱…...
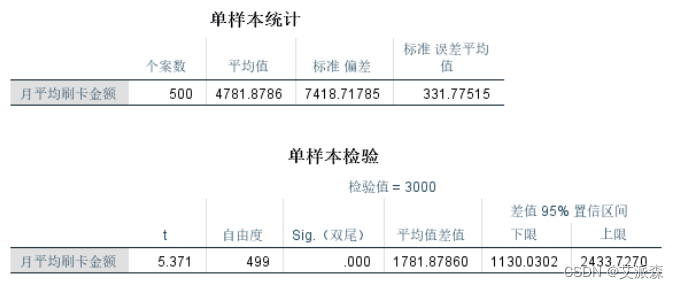
【SPSS】单样本T检验分析详细操作教程(附案例实战)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
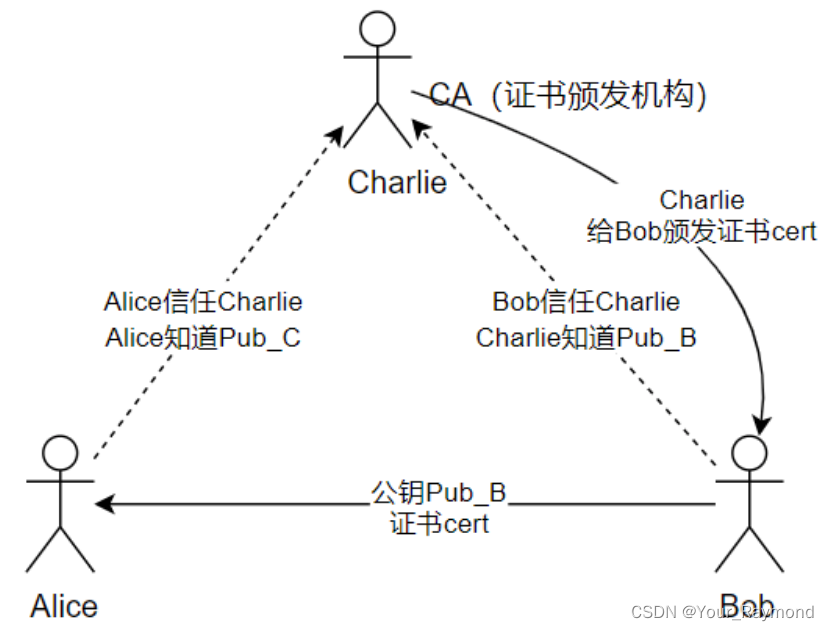
计算机网络笔记、面试八股(三)—— HTTPS协议
本章目录3. HTTPS协议3.1 HTTPS协议简介3.2 SSL/TLS协议3.2.1 SSL/TLS功能的实现3.3 HTTP和HTTPS的区别3.4 HTTPS协议的优点3.5 HTTPS协议的缺点3.6 HTTPS协议的工作流程3.7 HTTPS是如何解决HTTP的缺点的3.7.1 解决内容可能被窃听的问题——加密3.7.1.1 方法1.对称加密3.7.1.2 …...
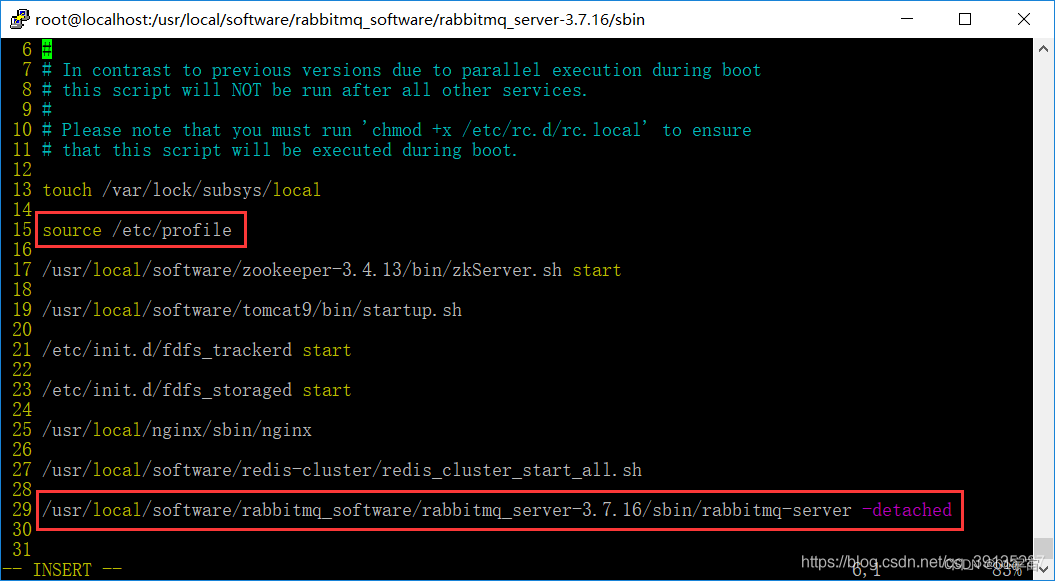
浅谈liunx init.d 和 rc.local 两种起动方式
浅谈liunx init.d 和 rc.local 两种起动方式 以rabbitmq 举例 (一).init.d 方式 开机自动重启设置 1.在/etc/init.d 目录下新建一个 rabbitmq [rootlocalhost init.d]# vi rabbitmq具体脚本如下所示: #!/bin/bash # # chkconfig: 2345 …...

元宇宙+教育,正在引发哪些剧烈变革?机会在哪里?丨圆桌实录
图片来源:由无界AI绘画工具生成2月23日,温州元宇宙创新中心为2023年第一批申请入驻的项目企业举办了签约仪式。温州临境网络科技有限公司、温州好玩文化产业有限公司、温州云兮科技有限公司(筹)等企业完成签约。这意味着ÿ…...
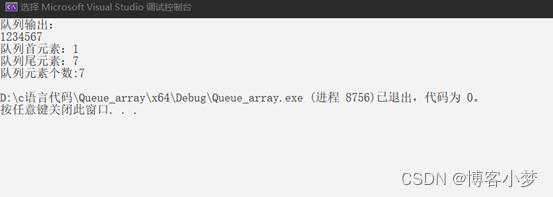
追梦之旅【数据结构篇】——详解C语言实现顺序队列
详解C语言实现顺序队列~😎前言🙌预备小知识🙌队列的概念及结构😊1.顺序队列头文件编写🙌2.Queue.c文件的编写🙌1)队列的初始化函数实现😊2)队列的销毁函数实现Ƕ…...

使用自己的数据集Fine-tune PaddleHub预训练模型
使用自己的数据Fine-tune PaddleHub预训练模型 果农需要根据水果的不同大小和质量进行产品的定价,所以每年收获的季节有大量的人工对水果分类的需求。基于人工智能模型的方案,收获的大堆水果会被机械放到传送带上,模型会根据摄像头拍到的图片…...

带组态物联网平台源码 代码开源可二次开发 web MQTT Modbus
物联网IOT平台开发辅助文档 技术栈:JAVA [ springmvc / spring / mybatis ] 、Mysql 、Html 、 Jquery 、css 使用协议和优势: TCP/IP、HTTP、MQTT 通讯协议 1.1系统简介 IOT通用物联网系统平台带组态,是一套面向通用型业务数据处理的系统…...

计算机网络的发展历程
计算机网络的历史可以追溯到20世纪60年代。那个时候,计算机还非常昂贵,只有少数大型机可以被用于处理重要任务。这些大型机通常被安装在大型企业、政府机构和大学中。由于这些机器非常昂贵,许多企业、机构和大学只能通过终端连接来访问它们。…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
