极限熵和冗余度
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。
信息冗余度(多余度、剩余度)
在信息论中,信息冗余是传输消息所用数据位的数目与消息中所包含的实际信息的数据位的数目的差值。
数据压缩是一种用来消除不需要的冗余的方法,校验和是在经过有限信道容量的噪声信道中通信,为了进行错误校正而增加冗余的方法。
信息冗余度一译"信息剩余度"。是指一定数量的信号单元可能有的最大信息量与其包含的实际信息量之差。通常用R表示。为信号的实际信息量,Imax为同样数量的信号单元可能有的最大信息量。会使传信绩效降低,但能提高通讯的抗干扰能力。
-
表示信源在实际发出消息时所包含的多余信息。
-
冗余度:
-
信源符号间的相关性。
- 相关程度越大,信源的实际熵越小
-
信源符号分布的不均匀性。
- 等概率分布时信源熵最大。
-
log2N=H0(X)≥H1(X)≥H2(X)≥⋯≥H∞(X)\log _{2} N=H_{0}(X) \geq H_{1}(X) \geq H_{2}(X) \geq \cdots \geq H_{\infty}(X)log2N=H0(X)≥H1(X)≥H2(X)≥⋯≥H∞(X)
N=H0(X)N=H_{0}(X)N=H0(X):等概率分布时信源熵
N=H1(X)N=H_{1}(X)N=H1(X):相互独立
N=H1(X)N=H_{1}(X)N=H1(X):两者有关系
-
对于有记忆信源, 极限熵为
H∞(X)=limN→∞H(XN/X1⋯XN−1)=limN→∞1NH(X1⋯XN)H_{\infty}(X)=\lim _{N \rightarrow \infty} H(X_{N} / X_{1} \cdots X_{N-1})=\lim _{N \rightarrow \infty} \frac{1}{N} H(X_{1} \cdots X_{N}) H∞(X)=N→∞limH(XN/X1⋯XN−1)=N→∞limN1H(X1⋯XN)
这就是说需要传送某一信源的信息, 理论上只需要传送 H∞(X)H_{\infty}(X)H∞(X) 即可。但这必须掌握信源全部概率统计特性, 这显然是不现实的。实际上, 只能算出 Hm(X)H_{m}(X)Hm(X) 。那么与理论极限值相比, 就要多传送 Hm(X)−H∞(X)H_{m}(X)-H_{\infty}(X)Hm(X)−H∞(X)
为了定量地描述信源的有效性, 定义: 信息效率
η=H∞(X)Hm(X)\eta=\frac{H_{\infty}(X)}{H_{m}(X)} η=Hm(X)H∞(X)
冗余度
γ=1−η=1−H∞(X)Hm(X)\gamma=1-\eta=1-\frac{H_{\infty}(X)}{H_{m}(X)} γ=1−η=1−Hm(X)H∞(X)
冗余度
由于信源存在冗余度,即存在一些不必要传送的信息,因此信源也就存在进一步压缩其信息率的可能性。
信源冗余度越大,其进一步压缩的潜力越大。这是信源编码与数据压缩的前提与理论基础。
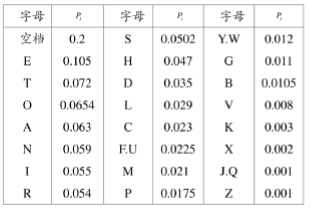
例:英文字母:
英文字母出现的概率如下表(含空格)
英文字母出现概率
若各个字母独立等概, 则信息熵
H0=log227=4.76bit/symH_{0}=\log _{2} 27=4.76 \mathrm{bit} / \mathrm{sym}H0=log227=4.76bit/sym
按照表计算独立不等概的信息熵
H1=−∑i=127pilogpi=4.03bit/symH_{1}=-\sum_{i=1}^{27} p_{i} \log p_{i}=4.03 \mathrm{bit} / \mathrm{sym}H1=−∑i=127pilogpi=4.03bit/sym
若只考虑一维相关性, 有 H2=3.32bit/symH_{2}=3.32 \mathrm{bit} / \mathrm{sym}H2=3.32bit/sym , 进一步考虑二维相关性, 有 H3=3.01bit/symH_{3}=3.01 bit/symH3=3.01bit/sym …
香农推断: H∞≅1.4bit/symH_{\infty} \cong 1.4 \mathrm{bit} / \mathrm{sym}H∞≅1.4bit/sym
- 从而:η=29%,γ=71%\eta=29 \%, \quad \gamma=71 \%η=29%,γ=71%
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.
相关文章:

极限熵和冗余度
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 信息冗余度(多余度、剩余…...

女生学习大数据专业未来前景怎么样
学习大数据与性别没有什么太大关系,各有优势。就目前的发展前景来说,大数据还是非常不错的,至于好不好就业就要看你个人学习的怎么样,以及学历是否过关了~ 据《新职业——大数据工程技术人员就业景气现状分析报告》显示ÿ…...
主题模型实践
目录 一.TF-IDF 二.LSI 三.相似度 四.主题和主题分布 五. LDA计算的相似度 六.LDA过程 七.主题 八.主题和主题分布 九.数据处理流程 十.常用正则表达式 十一.代码 一.TF-IDF 二.LSI 三.相似度 四.主题和主题分布 五. LDA计算的相似度 六.LDA过程 七.主题 八.主题和主…...

按字典序排列的最小的等价字符串[拆解并查集]
并查集前言一、按字典序排列的最小的等价字符串二、并查集总结参考文献前言 并查集有什么用?并查集是什么?搞懂这两个问题,相关的并查集问题就变得非常easy! 一、按字典序排列的最小的等价字符串 二、并查集 有一种方法&#x…...

操作系统——6.系统调用
目录 1.概述 2.系统调用的定义和作用 2.1 定义 2.2 功能 2.3 分类 3.系统调用和库函数的区别 4.系统调用背后的过程 5.小结 1.概述 这篇文章我们主要来介绍一下操作系统中的系统调用,下面来看一下具体的框架图: 2.系统调用的定义和作用 2.1 定…...

JavaScript DOM操作
目录 获取元素: 修改元素属性: 添加、删除、替换元素: 修改样式: DOM(文档对象模型)是一种用于操作 HTML 和 XML 文档的 API。JavaScript 通过 DOM API 可以访问和操作页面中的元素、属性和样式等。 获…...

【数据结构】顺序表
文章目录前言初始化顺序表打印顺序表检查容量判空顺序表数据个数尾部插入尾部删除头部插入头部删除在pos位置插入数据删除pos位置的数据查找数据修改数据销毁顺序表整体代码写在最后前言 顺序表作为数据结构中的小小弟,还是很好应付的。说到数据结构,顺序…...

【人工智能 AI 】RPA 架构师需要具备的技能有哪些?RPA Solution Architect
RPA 架构师需要具备的技能有哪些?使用markdown格式,不少于3000字,细化到3级目录。 文章目录 一、RPA架构师需要具备的技能1. 对RPA的理解2. 对RPA技术的熟练掌握2.1 RPA系统的架构模式2.2 RPA软件的操作模式2.3 RPA程序的编写方式3. 对RPA应用的知识4. 对软件开发的基本知识…...
【模拟集成电路】鉴频鉴相器设计(Phase Frequency Detector,PFD)
鉴频鉴相器设计(Phase Frequency Detector,PFD)前言一、 PFD的工作原理二、 PFD电路设计(1)PFD电路图(2)D触发器电路图(3)与非门(NAND)电路图&…...
【Linux】进程间通信介绍 | 管道
🌠 作者:阿亮joy. 🎆专栏:《学会Linux》 🎇 座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录👉进程间通信…...

这次说说腾讯的一场 35K—55K 的 Android 高工面试
一、面试的由来 事情是这样的,因为跟公司发展一些想法的不同,早在十月份的时候就有了跳槽的想法,但是碍于老大的面子就一直就没有跟人事说出口,打算着等到年后金三银四在试试跳槽。 但是发生一件事终于让我忍不住了,…...
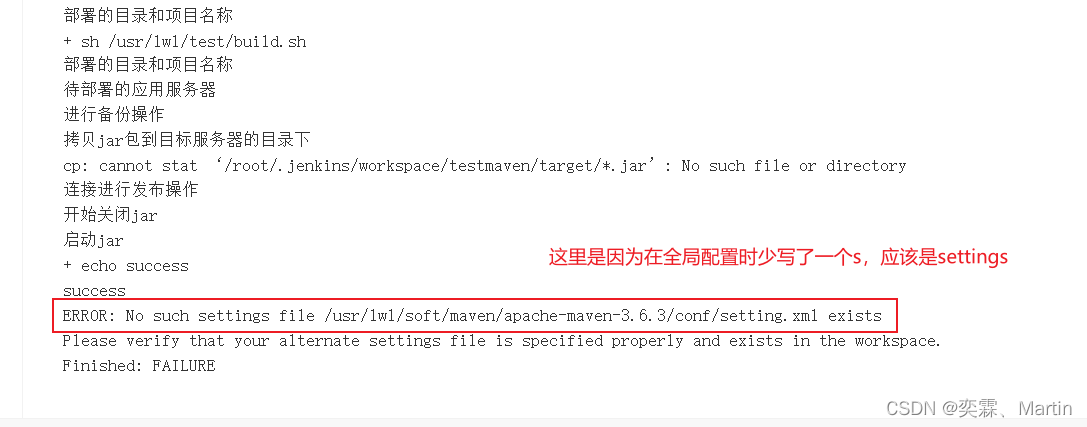
Jenkins第一讲
目录 一、Jenkins 1.1 敏捷开发与持续集成 1.1.1 敏捷开发 1.1.2 持续集成 1.2 持续集成工具 1.2.1 jenkins和hudson 1.2.2 技术组合 1.2.3 部署方式对比 1.3 安装Jenkins 1.3.1 下载Jenkins的war包 1.3.2 开启Jenkins 1.4 Jenkins全局安全配置 1.5 使用Jenkins部…...

变分推断 | MATLAB实现VBMC变分贝叶斯蒙特卡洛模拟的贝叶斯推断
变分推断 | MATLAB实现变分贝叶斯蒙特卡洛模拟的贝叶斯推断 目录 变分推断 | MATLAB实现变分贝叶斯蒙特卡洛模拟的贝叶斯推断效果一览基本介绍研究内容模型描述模型设计参考资料效果一览 基本介绍 MATLAB实现变分贝叶斯蒙特卡洛模拟的贝叶斯推断。变分贝叶斯蒙特卡洛(VBMC)是…...

代码随想录【Day25】| 216. 组合总和 III、17. 电话号码的字母组合
216. 组合总和 III 题目链接 题目描述: 找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。 说明: 所有数字都是正整数。 解集不能包含重复的组合。 示例 1: 输入: k 3, n 7 输…...
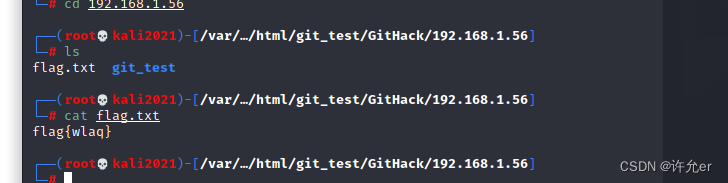
web中git漏洞的形成的原理及使用
目录 1.Git漏洞的成因 1.不正确的权限设置: 2.代码注入漏洞: 3.未经身份验证的访问: 4.非安全传输: 5.跨站脚本攻击(XSS): 2.git泄露环境的搭建 git init: git add࿱…...
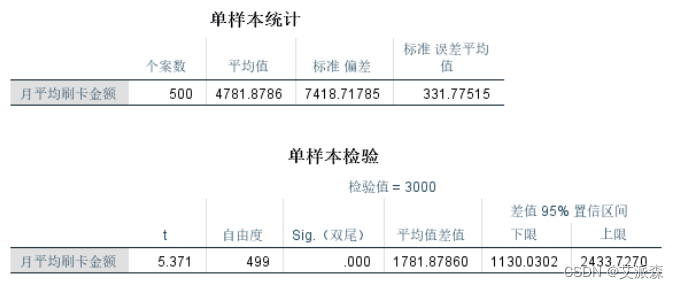
【SPSS】单样本T检验分析详细操作教程(附案例实战)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
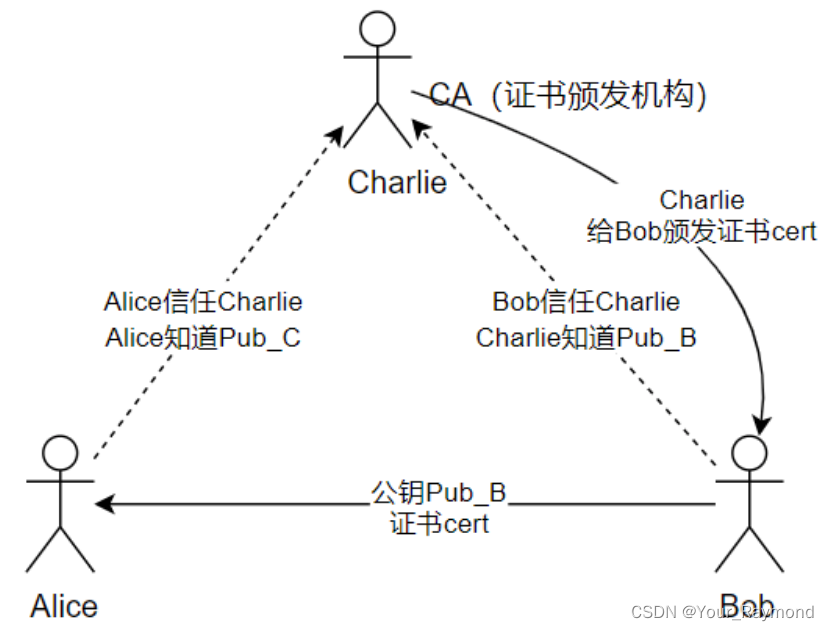
计算机网络笔记、面试八股(三)—— HTTPS协议
本章目录3. HTTPS协议3.1 HTTPS协议简介3.2 SSL/TLS协议3.2.1 SSL/TLS功能的实现3.3 HTTP和HTTPS的区别3.4 HTTPS协议的优点3.5 HTTPS协议的缺点3.6 HTTPS协议的工作流程3.7 HTTPS是如何解决HTTP的缺点的3.7.1 解决内容可能被窃听的问题——加密3.7.1.1 方法1.对称加密3.7.1.2 …...
浅谈liunx init.d 和 rc.local 两种起动方式
浅谈liunx init.d 和 rc.local 两种起动方式 以rabbitmq 举例 (一).init.d 方式 开机自动重启设置 1.在/etc/init.d 目录下新建一个 rabbitmq [rootlocalhost init.d]# vi rabbitmq具体脚本如下所示: #!/bin/bash # # chkconfig: 2345 …...

元宇宙+教育,正在引发哪些剧烈变革?机会在哪里?丨圆桌实录
图片来源:由无界AI绘画工具生成2月23日,温州元宇宙创新中心为2023年第一批申请入驻的项目企业举办了签约仪式。温州临境网络科技有限公司、温州好玩文化产业有限公司、温州云兮科技有限公司(筹)等企业完成签约。这意味着ÿ…...
追梦之旅【数据结构篇】——详解C语言实现顺序队列
详解C语言实现顺序队列~😎前言🙌预备小知识🙌队列的概念及结构😊1.顺序队列头文件编写🙌2.Queue.c文件的编写🙌1)队列的初始化函数实现😊2)队列的销毁函数实现Ƕ…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...