从代码入手理解卡尔曼滤波器的原理之使用Eigen实现二维卡尔曼滤波器(七)
当然可以。现在,给定了矩阵和向量的具体定义,我们可以更详细地解释这些变量的意义,并确定卡尔曼滤波器的维度。
-
F (状态转移矩阵):
F是一个2x2的矩阵,给定为:1 0 0 1
这意味着系统的状态从时刻
t到t+1没有实质变化,即每个状态都保持不变。 -
H (观测矩阵):
H也是一个2x2的矩阵,与单位矩阵相同:1 0 0 1
这意味着观测值直接等于状态值,没有任何转换。
-
Q (过程噪声协方差矩阵):
Q描述了过程噪声,是一个2x2的矩阵:0.01 0 0 0.01
这意味着两个状态的不确定性都是0.01,并且它们之间没有相关性。
-
R (测量噪声协方差矩阵):
R描述了观测过程中的噪声,也是一个2x2的矩阵:0.1 0 0 0.1
这表明观测值有较大的不确定性,并且两个观测值之间没有相关性。
-
x0 (初始状态向量):
x0是一个2x1的向量,所有元素都
相关文章:
)
从代码入手理解卡尔曼滤波器的原理之使用Eigen实现二维卡尔曼滤波器(七)
当然可以。现在,给定了矩阵和向量的具体定义,我们可以更详细地解释这些变量的意义,并确定卡尔曼滤波器的维度。 F (状态转移矩阵): F 是一个2x2的矩阵,给定为:1 0 0 1这意味着系统的状态从时刻t到t+1没有实质变化,即每个状态都保持不变。 H (观测矩阵): H 也是一个2x2的矩…...

文件的操作
前言:哈喽小伙伴们好久不见,国庆假期已经结束,接下来我们还是要马不停蹄的投入到学习当中,只有尽快调整状态回归学习,才能弯道超车。 今天我们一起来学习C语言——文件操作。 本篇文章讲到的所有函数均需要头文件#inc…...
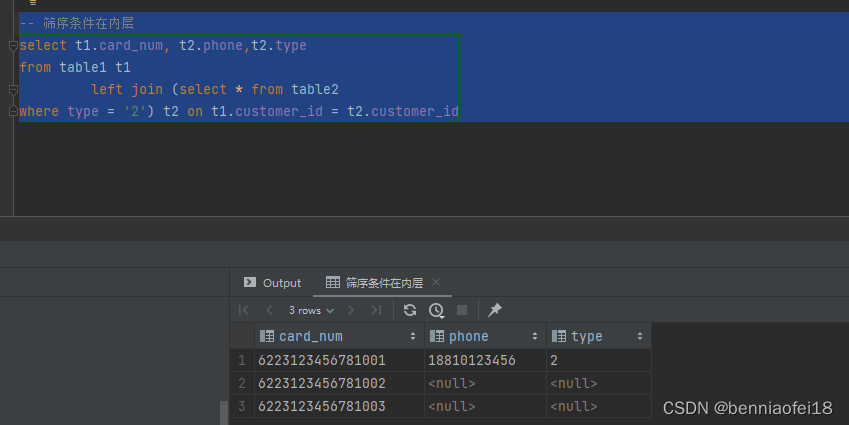
left join时筛选条件对查询结果的
-- 创建表 CREATE TABLE table1 (id int(11) NOT NULL AUTO_INCREMENT,card_num varchar(60) DEFAULT NULL,customer_id varchar(60) DEFAULT NULL,PRIMARY KEY (id) ) ENGINE InnoDBAUTO_INCREMENT 12DEFAULT CHARSET utf8mb4 COMMENT 测试表1;-- 创建表 CREAT…...

CVE-2020-9483 apache skywalking SQL注入漏洞
漏洞概述 当使用H2 / MySQL / TiDB作为Apache SkyWalking存储时,通过GraphQL协议查询元数据时,存在SQL注入漏洞,该漏洞允许访问未指定的数据。 Apache SkyWalking 6.0.0到6.6.0、7.0.0 H2 / MySQL / TiDB存储实现不使用适当的方法来设置SQL参…...
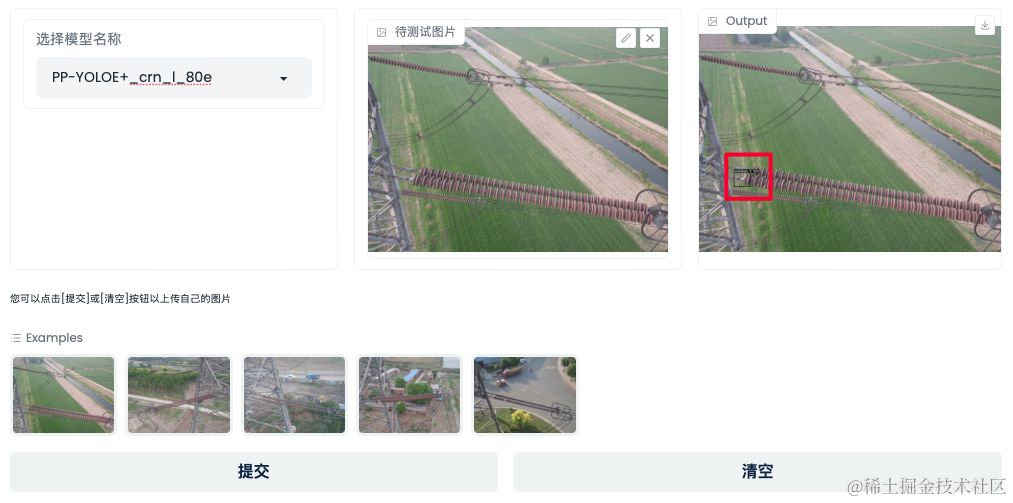
PaddleX解决分类、检测两大场景问题?实战精讲教程来了!
AI技术加速数字化进程,从制造、交通、能源等基础行业,到医疗、城市、零售、家居等与人们日常生活息息相关的行业,AI技术推动了数字化变革,也不断赋能于千行百业,但产业落地实践中依然面临着数据、算法等诸多困难。为了…...
)
Hive用户中文使用手册系列(二)
命令和 CLI 语言手册命令 命令是 non-SQL statements,例如设置 property 或添加资源。它们可以在 HiveQL 脚本中使用,也可以直接在CLI或Beeline中使用。 命令描述退出使用 quit 或 exit 退出交互式 shell。重启将 configuration 重置为默认值(从 Hive…...
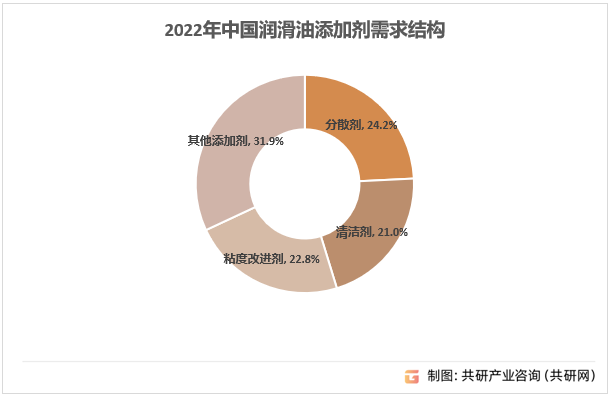
2023年中国清净剂行业需求现状及前景分析[图]
清净剂用于中和由于燃烧和润滑油氧化产生的酸性物质,并清除颗粒和污物。这类杂质在油中的溶解度有限,因此,清净剂可以最大程度减少沉积物的生成,降低污染,提高环保排放标准。成熟产品有磺酸盐、硫化烷基酚盐、烷基水杨…...

文心一言 VS 讯飞星火 VS chatgpt (115)-- 算法导论10.2 8题
八、用go语言,说明如何在每个元素仅使用一个指针 x.np(而不是通常的两个指针 next和prev)的下实现双向链表。假设所有指针的值都可视为 k 位的整型数,且定义x.npx.next XOR x.prev,即x.nert和x.prev 的 k 位异或。(NIL 的值用0表示。)注意要说…...

Redis的BitMap实现分布式布隆过滤器
布隆过滤器(Bloom Filter)是一种高效的概率型数据结构,用于判断一个元素是否属于一个集合。它通过使用哈希函数和位数组来存储和查询数据,具有较快的插入和查询速度,并且占用空间相对较少。 引入依赖 <!--切面--&…...

【linux API分析】module_init
linux版本:4.19 module_init()与module_exit()用于驱动的加载,分别是驱动的入口与退出函数 module_init():内核启动时或动态插入模块时调用module_exit():驱动移除时调用 本篇文章介绍module_init() module_init() module_init…...
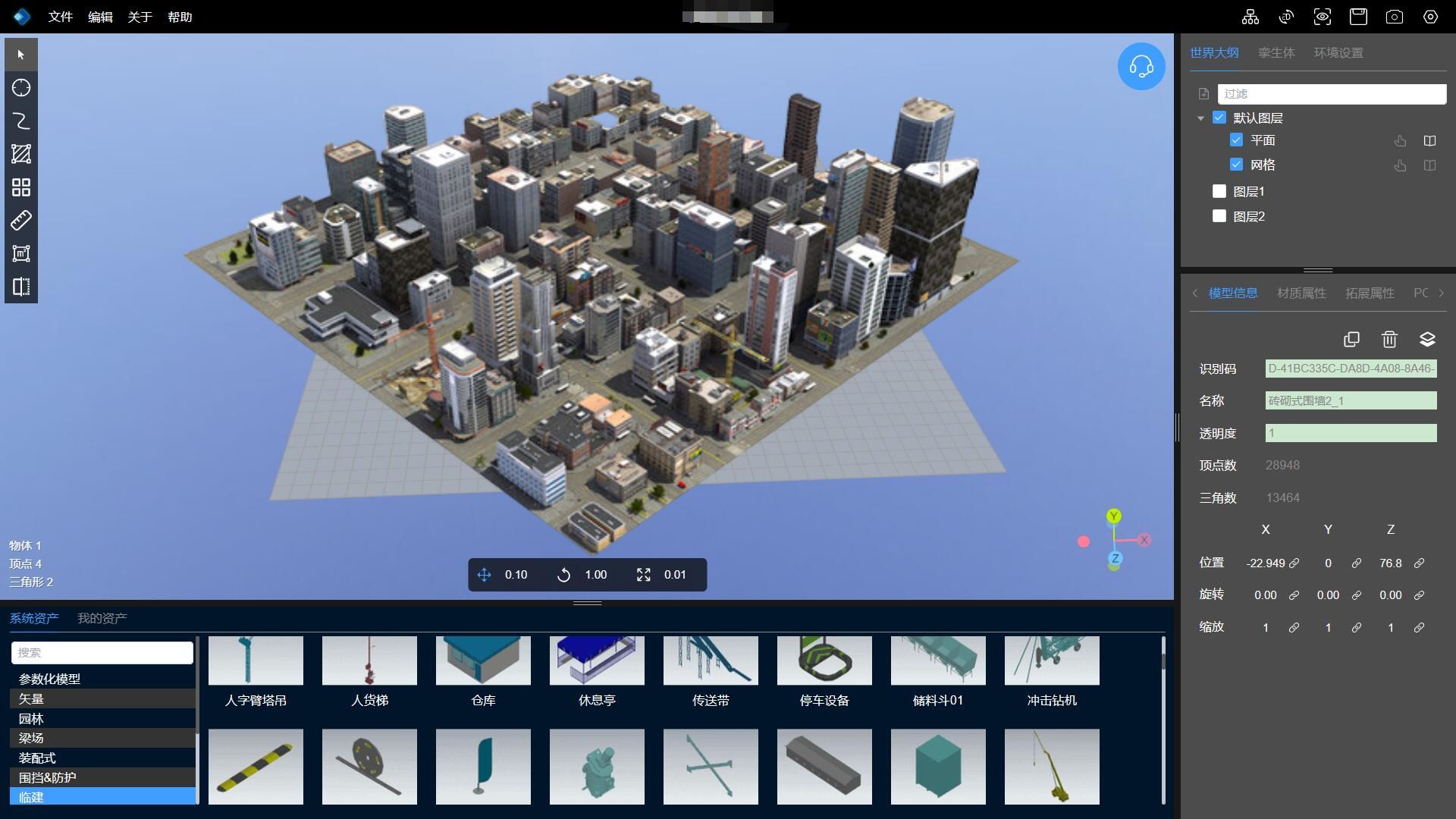
NSDT孪生编辑器助力智慧城市
技术有能力改变城市的运作方式,提高效率,为游客和居民提供更好的体验,实现更可持续的运营和更好的决策。 当今城市面临的主要挑战是什么,成为智慧城市如何帮助克服这些挑战? 我们生活在一个日益城市化的世界…...

如何优雅的实现接口统一调用
耦合问题 有些时候我们在进行接口调用的时候,比如说一个push推送接口,有可能会涉及到不同渠道的推送,以我目前业务场景为例,我做结算后端服务的,会与金蝶财务系统进行交互,那么我结算后端会涉及到多个结算…...
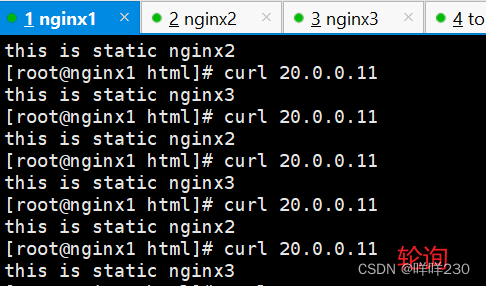
tomcat、nginx实现四层转发+七层代理+动静分离实验
实验环境: nginx1——20.0.0.11——客户端 静态页面: nginx2——20.0.0.21——代理服务器1 nginx3——20.0.0.31——代理服务器2 动态页面: tomcat1——20.0.0.12——后端服务器1 tomcat2——20.0.0.22——后端服务器2 实验步骤&…...
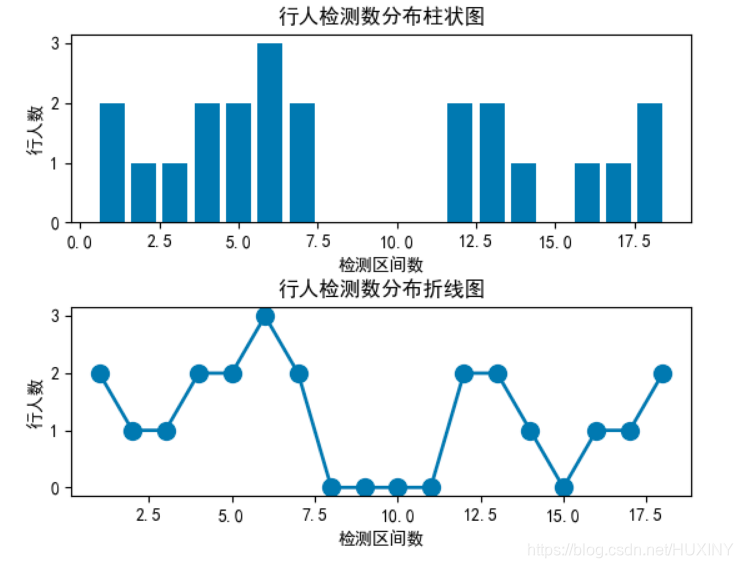
交通目标检测-行人车辆检测流量计数 - 计算机竞赛
文章目录 0 前言1\. 目标检测概况1.1 什么是目标检测?1.2 发展阶段 2\. 行人检测2.1 行人检测简介2.2 行人检测技术难点2.3 行人检测实现效果2.4 关键代码-训练过程 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 毕业设计…...

Java Excel转PDF,支持xlsx和xls两种格式, itextpdf【即取即用】
Java Excel转PDF itextpdf,即取即用 工具方法一、使用方式1、本地转换2、网络下载 二、pom依赖引入三、工具方法三、引文 本篇主要为工具方法整理,参考学习其他博主文章做了整理,方便使用。 工具方法 一、使用方式 1、本地转换 导入依赖创…...

重生奇迹mu宠物带来不一样的体验
重生奇迹mu宠物有什么作用? 全新版本中更是推出了各种宠物,在玩游戏时还可以带着宠物,一起疯狂的刷怪等等,可以为玩家带来非常不错的游戏体验,那么下面就来给大家说说各种宠物适合做什么事情。 1、强化恶魔适合刷怪 …...
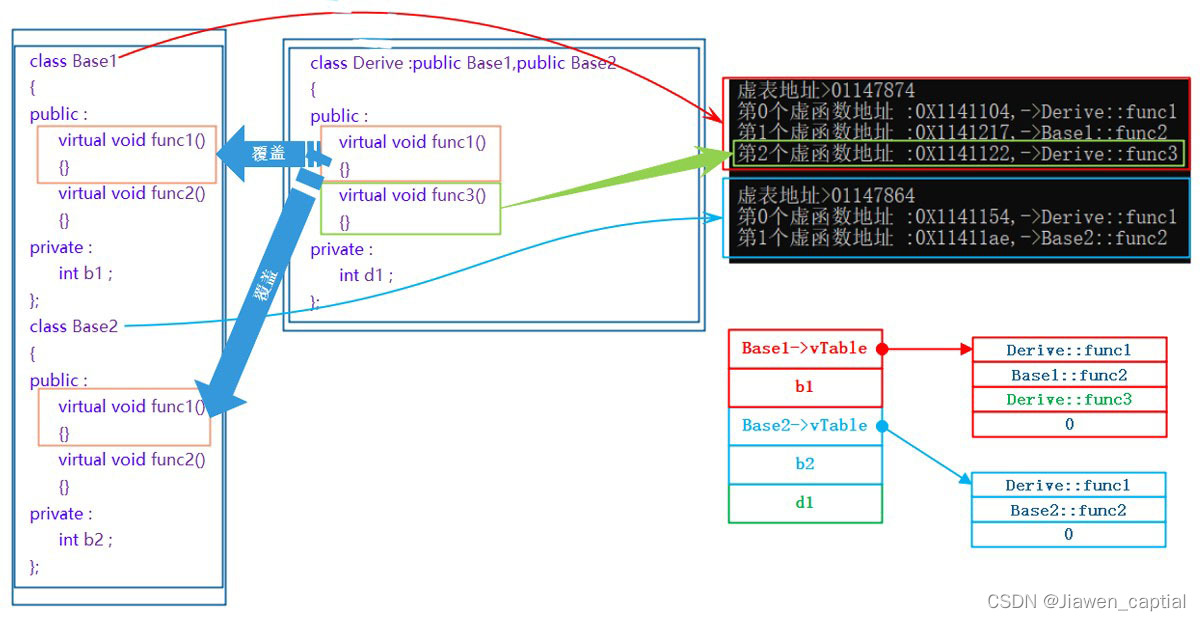
【C++笔记】多态的原理、单继承和多继承关系的虚函数表、 override 和 final、抽象类、重载、覆盖(重写)、隐藏(重定义)的对比
1.final关键字 引出:设计一个不能被继承的类。有如下方法: class A { private:A(int a0):_a(a){} public:static A CreateOBj(int a0){return A(a);} protected:int _a; } //简介限制,子类构成函数无法调用父类构造函数初始化 //子类的构造…...
安装thinkphp6并使用多应用模式,解决提示路由不存在解决办法
1. 安装稳定版tp框架 composer create-project topthink/think tptp是安装完成的目录名称 ,可以根据自己需要修改。 如果你之前已经安装过,那么切换到你的应用根目录下面,然后执行下面的命令进行更新: composer update topthin…...

FPGA笔试
1、FPGA结构一般分为三部分:可编程逻辑块(CLB)、可编程I/O模块和可编程内部连线。 2 CPLD的内部连线为连续式布线互连结构,任意一对输入、输出端之间的延时是固定 ;FPGA的内部连线为分段式布线互连结构,各…...

Pytorch:cat、stack、squeeze、unsqueeze的用法
Pytorch:cat、stack、squeeze、unsqueeze的用法 torch.cat 在指定原有维度上链接传入的张量,所有传入的张量都必须是相同形状 torch.cat(tensors, dim0, *, outNone) → Tensor tensor:相同形状的tensor dim:链接张量的维度,不能超过传入张…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...
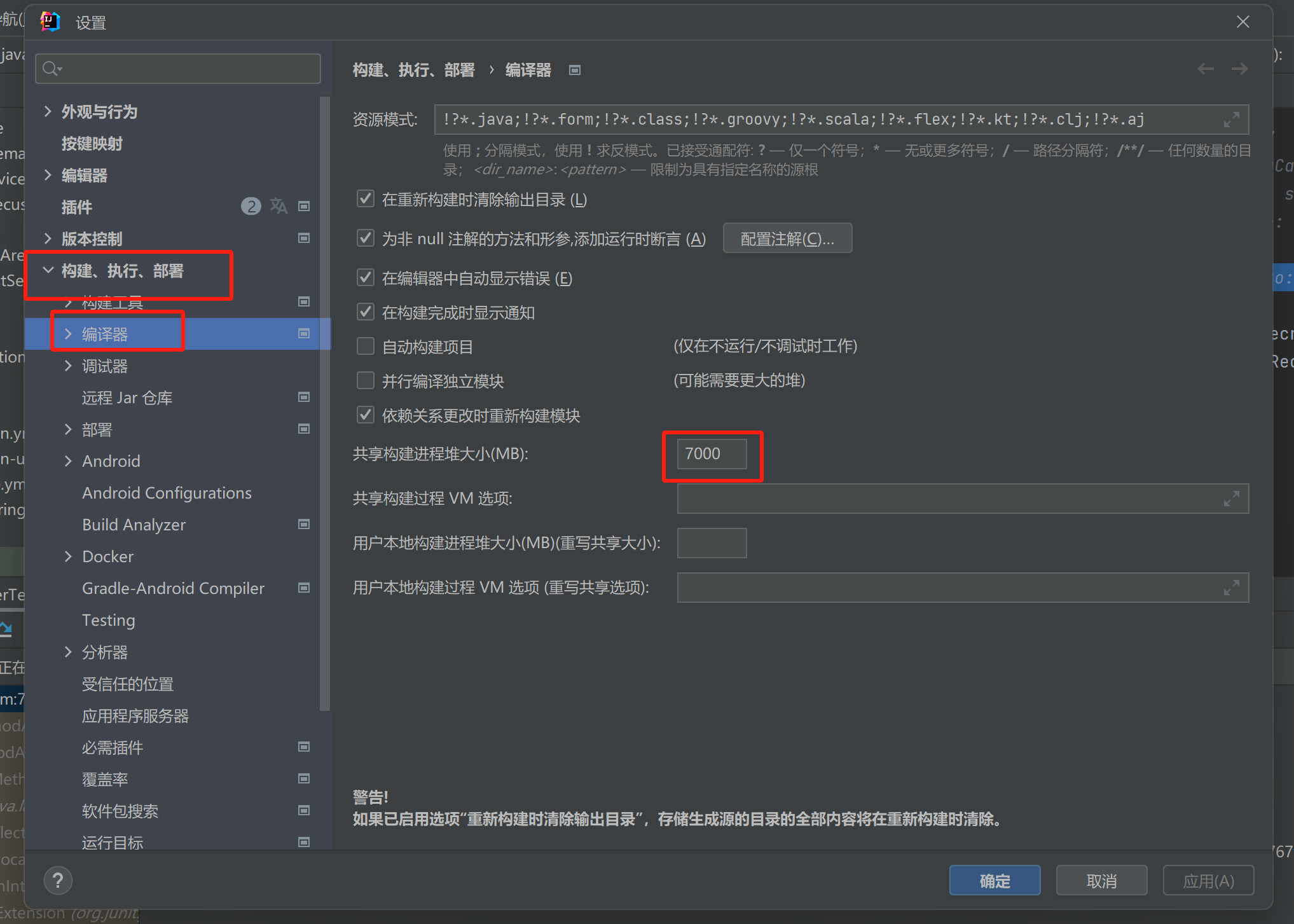
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...

IP选择注意事项
IP选择注意事项 MTP、FTP、EFUSE、EMEMORY选择时,需要考虑以下参数,然后确定后选择IP。 容量工作电压范围温度范围擦除、烧写速度/耗时读取所有bit的时间待机功耗擦写、烧写功耗面积所需要的mask layer...
