[NSSCTF 2nd]Math
原题py:
from secret import flag
from Crypto.Util.number import *
import gmpy2length = len(flag)
flag1 = flag[:length//2]
flag2 = flag[length//2:]
e = 65537m1 = bytes_to_long(flag1)
p = getPrime(512)
q = getPrime(512)
n = p*q
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)p1 = gmpy2.invert(p,q)
q1 = gmpy2.invert(q,p)
c = pow(m1,e,n)print("p1=",p1)
print("q1=",q1)
print("c=",c)
print("phi=",phi)"""
p1= 3020925936342826638134751865559091272992166887636010673949262570355319420768006254977586056820075450411872960532347149926398408063119965574618417289548987
q1= 4671408431692232396906683283409818749720996872112784059065890300436550189441120696235427299344866325968178729053396743472242000658751114391777274910146291
c= 25112054943247897935419483097872905208058812866572413543619256987820739973912338143408907736140292730221716259826494247791605665059462509978370784276523708331832947651238752021415405546380682507724076832547566130498713598421615793975775973104012856974241202142929158494480919115138145558312814378701754511483
phi= 57503658815924732796927268512359220093654065782651166474086873213897562591669139461637657743218269483127368502067086834142943722633173824328770582751298229218384634668803018140064093913557812104300156596305487698041934061627496715082394633864043543838906900101637618600513874001567624343801197495058260716932
"""m2 = bytes_to_long(flag2)
p = getPrime(1024)
q = getPrime(1024)
n = p * q
c = pow(m2, e, n)
hint = pow(2023 * p + 114514, q, n)
print("n=",n)
print("c=",c)
print("hint=",hint)"""
n= 12775720506835890504634034278254395430943267336816473660983646973423280986156683988190224391394224069040565587173690009193979401332176772774003070053150665425296356891182224095151626957780349726980433545162004592720236315207871365869074491602494662741551613634958123374477023452496165047922053316939727488269523121920612595228860205356006298829652664878874947173274376497334009997867175453728857230796230189708744624237537460795795419731996104364946593492505600336294206922224497794285687308908233911851722675754289376914626682400586422368439122244417279745706732355332295177737063024381192630487607768783465981451061
c= 11915755246503584850391275332434803210208427722294114071001100308626307947436200730224125480063437044802693983505018296915205479746420176594816835977233647903359581826758195341201097246092133133080060014734506394659931221663322724002898147351352947871411658624516142945817233952310735792476179959957816923241946083918670905682025431311942375276709386415064702578261223172000098847340935816693603778431506315238612938066215726795441606532661443096921685386088202968978123769780506210313106183173960388498229061590976260661410212374609180449458118176113016257713595435899800372393071369403114116302366178240855961673903
hint= 3780943720055765163478806027243965253559007912583544143299490993337790800685861348603846579733509246734554644847248999634328337059584874553568080801619380770056010428956589779410205977076728450941189508972291059502282197067064652703679207594494311426932070873126291964667101759741689303119878339091991064473009603015444698156763131697516348762529243379294719509271792197450290763350043267150173332933064667716343268081089911389405010661267902446894363575630871542572200564687271311946580866369204751787686029541644463829030926902617740142434884740791338666415524172057644794094577876577760376741447161098006698524808
"""审计代码:
此题分为两个部分,第一部分是一道告知我们p1 = gmpy2.invert(p,q)、q1 = gmpy2.invert(q,p)、c、phi四个条件,需要我们求出p和q的值,即可使用传统的rsa将未知的m分解的部分;
求解思路如下:
详细资料可参考:
https://github.com/pcw109550/write-up/tree/master/2019/HITCON/Lost_Modulus_Again
p1 = gmpy2.invert(p,q)
q1 = gmpy2.invert(q,p)
=>
p1*p = 1 + k1*q
q1*q = 1 + k2*p
=>相减
p*(p1 + k2) = q*(q1 + k1)
由于p和q都是素数,所以(p1 + k2) 必然整除q,(q1 + k1)必然整除p,将p、q用这两个值代替
phi(n) = (p-1)*(q-1) = p*q - (p+q) + 1
=>
phi(n) = (q1 + k1 - 1)*(p1 + k2 - 1)
=(q1 - 1) * (p1 - 1) + (q1 - 1) * k1 + (p1 - 1) * k2 + k1 * k2
=>
phi(n) = q1 * p1 - 1 + (p1 - 1) * (q1 * p1 - 1) / k1 + k1 * (q1 - 1) + (q1 - 1) * (p1 - 1)
# quadratic equation f(k1) = 0
(q1 - 1) * k1 ** 2 + (q1 * p1 - 1 - phi(n) + (q1 - 1) * (p1 - 1)) * k1 + (p1 - 1) * (q1 * p1 - 1) = 0
此时我们便可以建立一个以k1为系数的一元二次方程求解:
solve:
x = 3020925936342826638134751865559091272992166887636010673949262570355319420768006254977586056820075450411872960532347149926398408063119965574618417289548987
y = 4671408431692232396906683283409818749720996872112784059065890300436550189441120696235427299344866325968178729053396743472242000658751114391777274910146291
ct = 25112054943247897935419483097872905208058812866572413543619256987820739973912338143408907736140292730221716259826494247791605665059462509978370784276523708331832947651238752021415405546380682507724076832547566130498713598421615793975775973104012856974241202142929158494480919115138145558312814378701754511483
phi = 57503658815924732796927268512359220093654065782651166474086873213897562591669139461637657743218269483127368502067086834142943722633173824328770582751298229218384634668803018140064093913557812104300156596305487698041934061627496715082394633864043543838906900101637618600513874001567624343801197495058260716932from Crypto.Util.number import *
import gmpy2
e = 65537
d = inverse(e,phi)def solve(a, b, c):D = b ** 2 - 4 * a * c# assert gmpy2.is_square(D)x1 = (-b + gmpy2.isqrt(D)) // (2 * a)x2 = (-b - gmpy2.isqrt(D)) // (2 * a)return x1, x2a = x - 1
b = x * y - 1 + (x - 1) * (y - 1) - phi
c = (y - 1) * (x * y - 1)
k1, k2 = solve(a, b, c)
if (x * y - 1) % k1 == 0:k2 = (x * y - 1) // k1
elif (x * y - 1) % k2 == 0:k1, k2 = k2, (x * y - 1) // k2
else:assert Falsep, q = x + k2, y + k1
N = p * q
flag1 = long_to_bytes(pow(ct, d, N)).strip()
print(flag1)第二部分则是相似推导:
原题py:
m2 = bytes_to_long(flag2)
p = getPrime(1024)
q = getPrime(1024)
n = p * q
c = pow(m2, e, n)
hint = pow(2023 * p + 114514, q, n)
print("n=",n)
print("c=",c)
print("hint=",hint)"""
n= 12775720506835890504634034278254395430943267336816473660983646973423280986156683988190224391394224069040565587173690009193979401332176772774003070053150665425296356891182224095151626957780349726980433545162004592720236315207871365869074491602494662741551613634958123374477023452496165047922053316939727488269523121920612595228860205356006298829652664878874947173274376497334009997867175453728857230796230189708744624237537460795795419731996104364946593492505600336294206922224497794285687308908233911851722675754289376914626682400586422368439122244417279745706732355332295177737063024381192630487607768783465981451061
c= 11915755246503584850391275332434803210208427722294114071001100308626307947436200730224125480063437044802693983505018296915205479746420176594816835977233647903359581826758195341201097246092133133080060014734506394659931221663322724002898147351352947871411658624516142945817233952310735792476179959957816923241946083918670905682025431311942375276709386415064702578261223172000098847340935816693603778431506315238612938066215726795441606532661443096921685386088202968978123769780506210313106183173960388498229061590976260661410212374609180449458118176113016257713595435899800372393071369403114116302366178240855961673903
hint= 3780943720055765163478806027243965253559007912583544143299490993337790800685861348603846579733509246734554644847248999634328337059584874553568080801619380770056010428956589779410205977076728450941189508972291059502282197067064652703679207594494311426932070873126291964667101759741689303119878339091991064473009603015444698156763131697516348762529243379294719509271792197450290763350043267150173332933064667716343268081089911389405010661267902446894363575630871542572200564687271311946580866369204751787686029541644463829030926902617740142434884740791338666415524172057644794094577876577760376741447161098006698524808
"""hint = pow(2023 * p + 114514, q, n)
=>
hint = (2023 * p + 114514)^q mod p
hint = 114514^q + k1 * p
114514^q = hint - k1*p
(114514^q)^p = (hint - k1*p)^p
114514^n = p*(.....) + hint^p
=>
114514^n = hint^p mod p = hint
所以 114514^n - hint^p,必然是p的倍数,p和q便可以求出。
solve:
nn = 12775720506835890504634034278254395430943267336816473660983646973423280986156683988190224391394224069040565587173690009193979401332176772774003070053150665425296356891182224095151626957780349726980433545162004592720236315207871365869074491602494662741551613634958123374477023452496165047922053316939727488269523121920612595228860205356006298829652664878874947173274376497334009997867175453728857230796230189708744624237537460795795419731996104364946593492505600336294206922224497794285687308908233911851722675754289376914626682400586422368439122244417279745706732355332295177737063024381192630487607768783465981451061
cc = 11915755246503584850391275332434803210208427722294114071001100308626307947436200730224125480063437044802693983505018296915205479746420176594816835977233647903359581826758195341201097246092133133080060014734506394659931221663322724002898147351352947871411658624516142945817233952310735792476179959957816923241946083918670905682025431311942375276709386415064702578261223172000098847340935816693603778431506315238612938066215726795441606532661443096921685386088202968978123769780506210313106183173960388498229061590976260661410212374609180449458118176113016257713595435899800372393071369403114116302366178240855961673903
hint = 3780943720055765163478806027243965253559007912583544143299490993337790800685861348603846579733509246734554644847248999634328337059584874553568080801619380770056010428956589779410205977076728450941189508972291059502282197067064652703679207594494311426932070873126291964667101759741689303119878339091991064473009603015444698156763131697516348762529243379294719509271792197450290763350043267150173332933064667716343268081089911389405010661267902446894363575630871542572200564687271311946580866369204751787686029541644463829030926902617740142434884740791338666415524172057644794094577876577760376741447161098006698524808p = GCD(pow(114514,nn,nn) - hint,nn)
q = nn//p
D = inverse(e,(p-1)*(q-1))
flag2 = long_to_bytes(pow(cc,D,nn))
print(flag2)将两次求解得到的flag相加即可。
相关文章:

[NSSCTF 2nd]Math
原题py: from secret import flag from Crypto.Util.number import * import gmpy2length len(flag) flag1 flag[:length//2] flag2 flag[length//2:] e 65537m1 bytes_to_long(flag1) p getPrime(512) q getPrime(512) n p*q phi (p-1)*(q-1) d gmpy2.i…...
uml知识点学习
https://zhuanlan.zhihu.com/p/659911315https://zhuanlan.zhihu.com/p/659911315软件工程分析设计图库目录 - 知乎一、结构化绘图1. 结构化——数据流图Chilan Yuk:1. 结构化——数据流图2. 结构化——数据字典Chilan Yuk:2. 结构化——数据字典3. 结构…...

JAVA学习日记1——JAVA简介及第一个java程序
简单记忆 JAVA SE :标准版,核心基础 JAVA EE:企业版,进阶 JDK:Java Development Kit,Java开发工具包,包含JRE JRE:Java Runtime Environment,Java运行时环境ÿ…...
之less)
Linux命令(102)之less
linux命令之less 1.less介绍 linux命令less是一个文本文件查看工具,它以一种交互的方式,逐页地显示文本文件的内容,并且可以在文件中进行搜索等定位 2.less用法 less [参数] filename less参数 参数说明-N显示每行的行号-i忽略搜索时的大…...

vue多条件查询
<template><div><input type"text" v-model"keyword" placeholder"关键字"><select v-model"category"><option value"">所有分类</option><option v-for"cat in categories&q…...

c 语言基础:L1-038 新世界
这道超级简单的题目没有任何输入。 你只需要在第一行中输出程序员钦定名言“Hello World”,并且在第二行中输出更新版的“Hello New World”就可以了。 输入样例: 无输出样例: Hello World Hello New World 程序源码: #incl…...

计算机算法分析与设计(13)---贪心算法(多机调度问题)
文章目录 一、问题概述1.1 思路分析1.2 实例分析 二、代码编写 一、问题概述 1.1 思路分析 1. 设有 n n n 个独立的作业 1 , 2 , … , n {1, 2, …, n} 1,2,…,n,由 m m m 台相同的机器 M 1 , M 2 , … , M m {M_1, M_2, …, M_m} M1,M2,…,Mm 进行加工处…...

小程序canvas层级过高真机遮挡组件的解决办法
文章目录 问题发现真机调试问题分析问题解决改造代码效果展示 问题发现 在小程序开发中需要上传图片进行裁剪,在实际真机调试中发现canvas层遮挡住了生成图片的按钮。 问题代码 <import src"../we-cropper/we-cropper.wxml"></import> <…...

番外8.1 配置+管理文件系统
Task01: Linux 文件系统结构; 可以进行Linux操作系统的文件权限管理与方式切换,可以应用磁盘与文件权限管理工具; 01:常见文件系统类型(Ext4[rhel6默认文件管理系统], 存储容量1 EB1073741824 GB; XFS[rhel 7/8默认的文…...

互联网Java工程师面试题·Java 总结篇·第八弹
目录 72、用 Java 的套接字编程实现一个多线程的回显(echo)服务器。 73、XML 文档定义有几种形式?它们之间有何本质区别?解析XML 文档有哪几种方式? 74、你在项目中哪些地方用到了 XML? 72、用 Java 的套…...
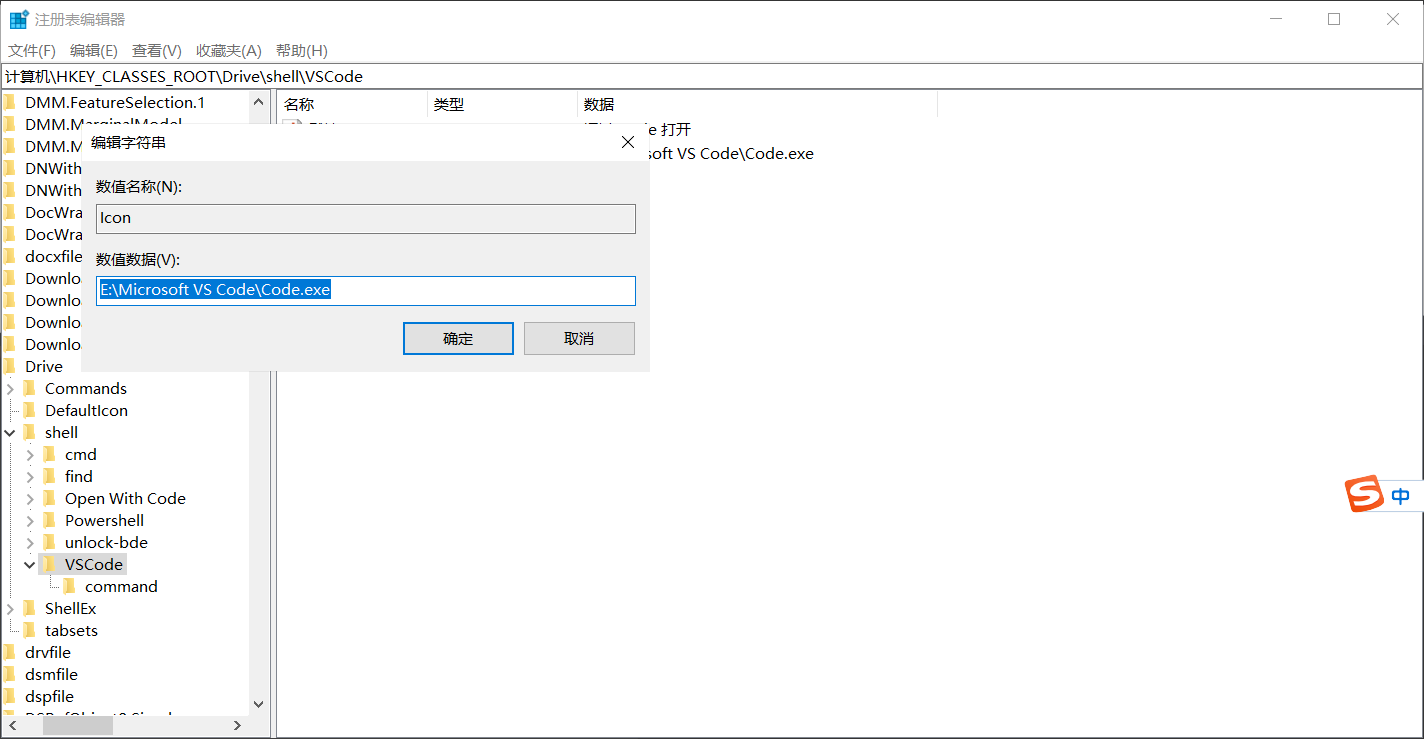
VSCode修改扩展和用户文件夹目录位置(Windows)
VSCode修改扩展和用户文件夹目录位置(Windows) 前言:方法前期准备:方法1(强推荐)方法2(不太推荐)方法3(好麻烦,不太推荐) 前言: VSCod…...

Spring 事务
文章目录 实现CURD(没加入事务前)1.加入依赖2.创建jdbc.properties3.配置Spring的配置文件4.数据库与测试表 基于注解的声明式事务准备工作测试模拟场景 加入事务①添加事务配置 Transactional注解标识的位置只读事务属性:超时事务属性&#…...
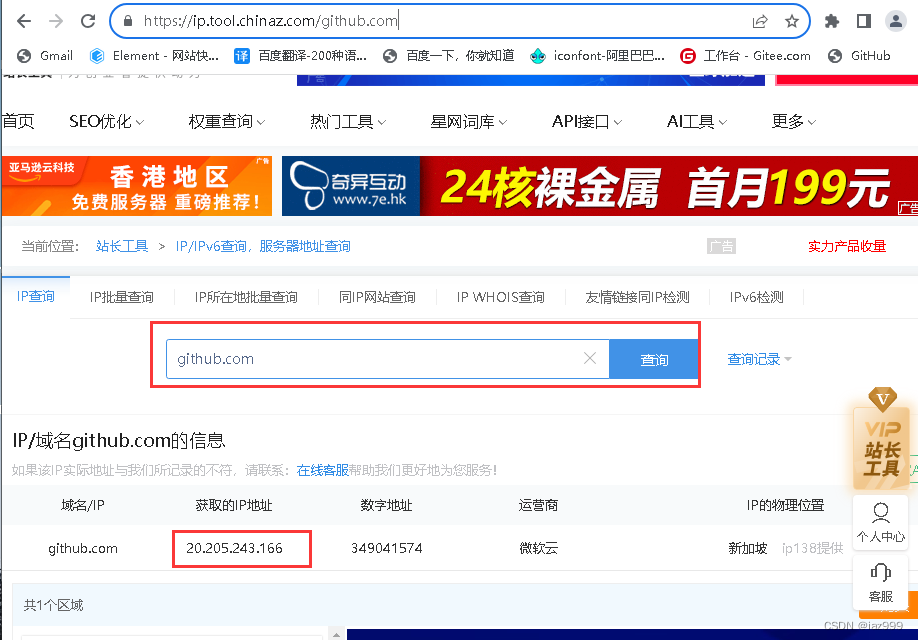
无法访问 github ,解决办法
一、使用代理(首选) 这种办法只需要更改github.com为代理的域名即可,使用方式与GitHub除了域名不同其他都一样,速度挺快,可登陆,可提交。 1、查看当前的代理: git config --global --get htt…...
SD卡与emmc的异同
eMMC与SD卡的异同: 物理尺寸和接口: eMMC:eMMC是一种嵌入式存储解决方案,通常采用BGA(Ball Grid Array)封装,焊接在电路板上。它没有标准的物理尺寸,而是以芯片的形式存在。SD卡&…...
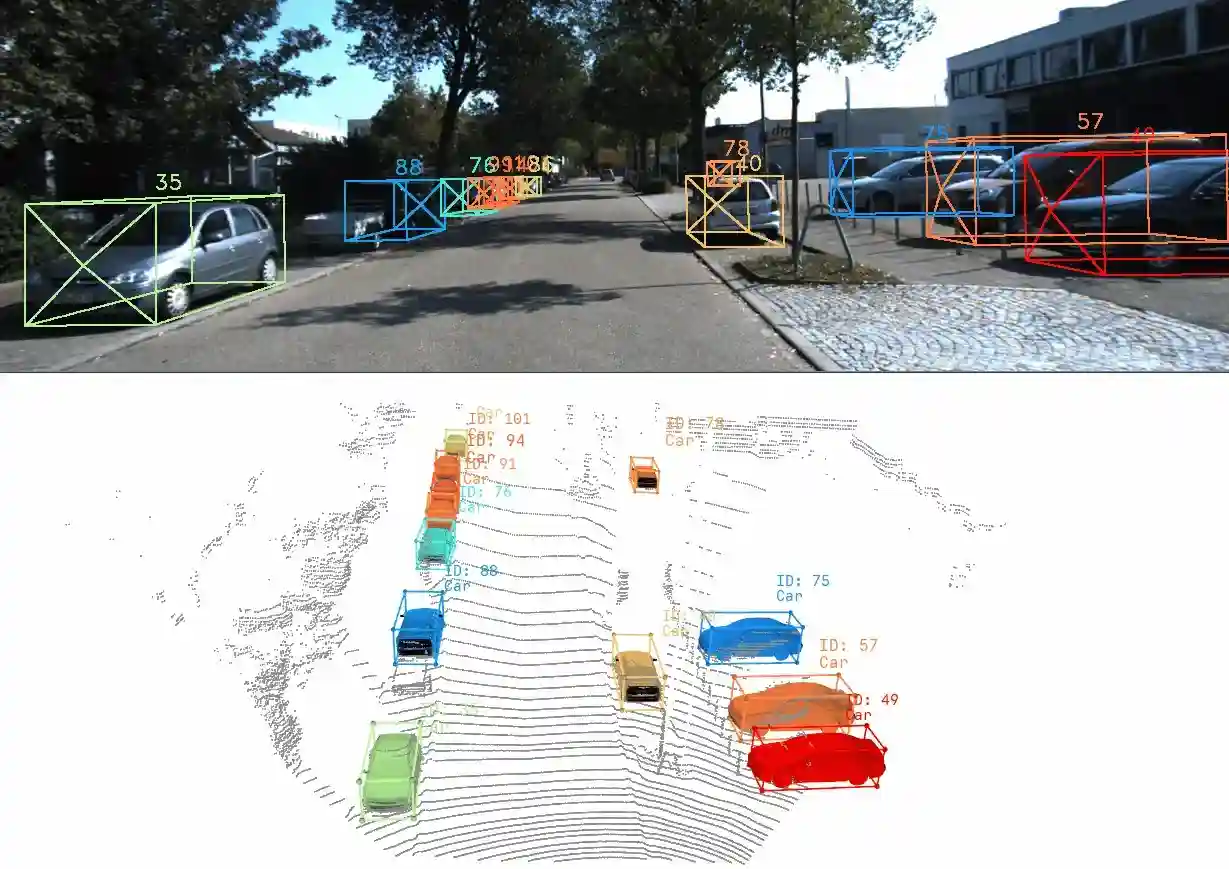
机器学习笔记 - 3D 对象跟踪极简概述
一、简述 大多数对象跟踪应用程序都是 2D 的。但现实世界是 3D 的,无论您是跟踪汽车、人、直升机、导弹,还是进行增强现实,您都需要使用 3D。在 CVPR 2022(计算机视觉和模式识别)会议上,已经出现了大量3D目标检测论文。 二、什么是 3D 对象跟踪? 对象跟踪是指随着时间的…...
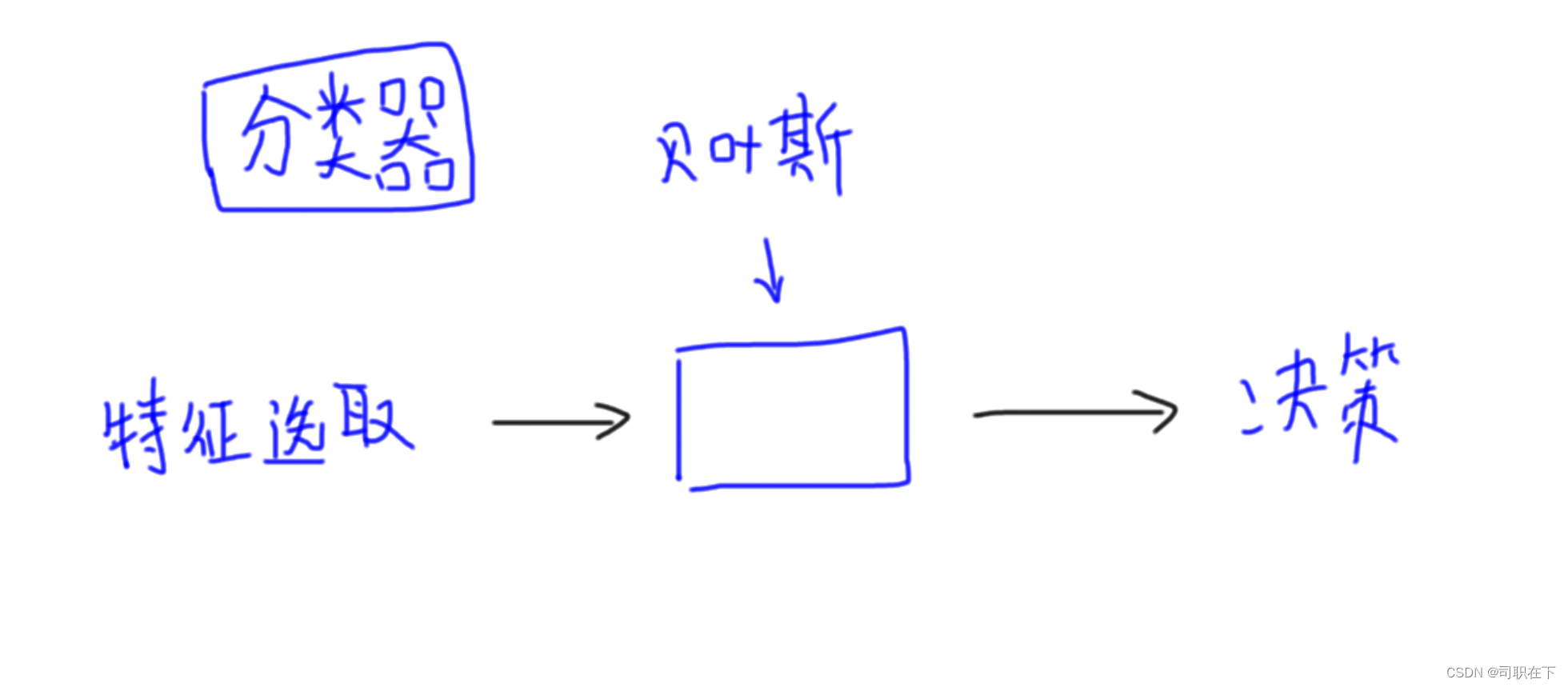
《机器学习----简单的分类器》第二章、朴素贝叶斯,项目:使用特征值给语句打标签
贝叶斯分类器 1,朴素贝叶斯算法1. 朴素贝叶斯算法、2. 算法思路3. 贝叶斯定理4.特征的选用的要求和处理 2,算法应用1 文本分类2 垃圾邮件过滤3 情感分析 3. 朴素贝叶斯的优缺点1. 优点2. 缺点 项目实践1,算法流程2,具体实现 1,朴素贝叶斯算法…...

01. 汇编LED驱动实验
01. 汇编LED驱动实验 汇编原理分析为什么要学习Cortex—A汇编STM32IO初始化流程IMX6UL初始化流程 汇编基础处理器内部数据传输指令存储器访问指令 编写驱动编译程序烧写bin文件 汇编原理分析 为什么要学习Cortex—A汇编 需要用汇编初始化一些SOC外设使用汇编初始化DDR&#x…...
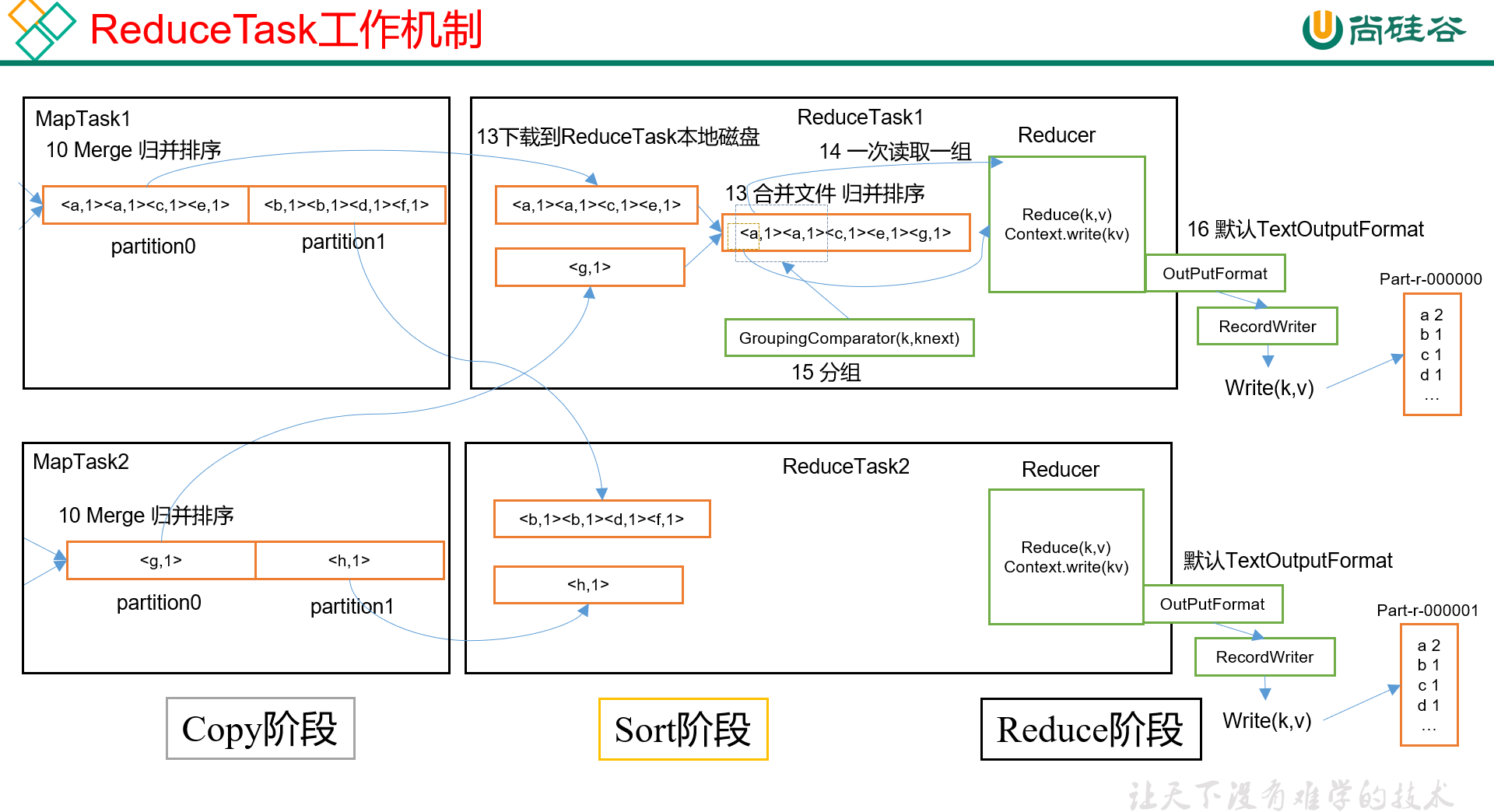
Hadoop3教程(二十):MapReduce的工作机制总结
文章目录 (109)MapTask工作机制(110)ReduceTask工作机制&并行度ReduceTask工作机制MapTask和ReduceTask的并行度决定机制 (122)MapReduce开发总结参考文献 (109)MapTask工作机制…...

浅谈AI大模型技术:概念、发展和应用
AI大模型技术是指使用超大规模的深度学习模型来解决各种复杂的人工智能问题,如自然语言处理、计算机视觉、多模态交互等。AI大模型技术具有强大的学习能力和泛化能力,可以在多种任务上取得优异的性能,但也面临着计算、存储、通信等方面的挑战…...
【Leetcode】212.单词搜索II(Hard)
一、题目 1、题目描述 给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表 words, 返回所有二维网格上的单词 。 单词必须按照字母顺序,通过 相邻的单元格 内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
