Spring中配置文件参数化
目录
一、什么是配置文件参数化
二、配置文件参数化的开发步骤
一、什么是配置文件参数化
配置文件参数化就是将Spring中经常需要修改的字符串信息,转移到一个更小的配置文件中。那么为什么要进行配置文件参数化呢?我们看一个代码
<bean id="connection" class="com.gl.demo.factory.ConnectionFactoryBean"><property name="driveClassName" value="com.mysql.jdbc.Driver"/><property name="url" value="jdbc:mysql://localhost:3306/test?useSSL=false"/><property name="username" value="root"/><property name="password" value="123456"/>
</bean>
这是之前配置数据库连接池的一个代码,虽然使用配置文件的方式已经很简洁了,但是如果我要频繁的修改呢?又或者是我这里的配置信息很多呢?这样就造成了代码的维护性变差,所以这就是为什么要将配置文件参数化的原因
二、配置文件参数化的开发步骤
1)首先,准备一个小的配置文件(.properties)用来存放需要转移的参数,这里就将需要注入的值转移到了小的配置文件中
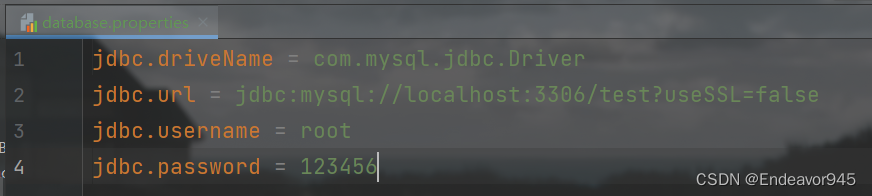
2)在原来的Spring配置文件中添加context标签来引入配置文件的位置,这个标签是Spring专门用来引入小的配置文件的,其中这个location就是配置文件存放的位置
<context:property-placeholder location="classpath:/database.properties"/>
3)由于原来的配置文件中的value值已经没有了,这里只需要使用一个${}包裹小配置文件中的key值就可了
<context:property-placeholder location="classpath:/database.properties"/><bean id="conn" class="com.gl.demo.factory.ConnectionFactoryBean"><property name="driveClassName" value="${jdbc.driveName}"></property><property name="url" value="${jdbc.url}"></property><property name="username" value="${jdbc.username}"></property><property name="password" value="${jdbc.password}"></property>
</bean>
相关文章:

Spring中配置文件参数化
目录 一、什么是配置文件参数化 二、配置文件参数化的开发步骤 一、什么是配置文件参数化 配置文件参数化就是将Spring中经常需要修改的字符串信息,转移到一个更小的配置文件中。那么为什么要进行配置文件参数化呢?我们看一个代码 <bean id"co…...
linux minicom 调试串口
1、使用方法 1. 打开终端 2. 输入命令:minicom -D /dev/ttyS0 3. 按下回车键,进入minicom终端界面 4. 在终端界面中发送指令或数据,查看设备返回的数据 5. 按下CtrlA,松开释放,再按下X,退出minicom2、一些…...

#力扣:2651. 计算列车到站时间@FDDLC
2651. 计算列车到站时间 - 力扣(LeetCode) 一、Java class Solution {public int findDelayedArrivalTime(int arrivalTime, int delayedTime) {return (arrivalTimedelayedTime)%24;} }...
小县城蔬菜配送小程序制作全攻略
随着互联网的普及和人们对生活品质要求的提高,越来越多的小县城开始开发蔬菜配送小程序,以满足当地居民对新鲜蔬菜的需求。制作一个小县城蔬菜配送小程序,需要经过以下步骤: 步骤一:登录乔拓云平台 首先,打…...

JavaPTA练习题 7-4 计算给定两数之间的所有奇数之和
本题目要求接收输入的2个整数a和b,然后输出a~b之间的所有奇数之和。 输入格式: 分别用两行输入两个整数a,b 输出格式: 输出a~b之间的所有奇数之和 输入样例: 在这里给出一组输入。例如: 1 30输出样例: 在这里给出相应的输出。例如: …...
基于SSM的大学校医管理系统
基于SSM的大学校医管理系统、学校医院管理系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 主页 登录系统 用户界面 管理员界面 摘要 大学校医管理系统…...

【递归、搜索与回溯算法】第一节.初识递归、搜索与回溯算法
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:递归、搜索与回溯算法 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!&am…...

第十二届蓝桥杯模拟赛第一期
A填空题 问题描述 如果整数a是整数b的整数倍,则称b是a的约数。 请问,有多少个正整数是2020的约数。 答案提交 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数࿰…...

【生成对抗网络】
生成对抗网络(Generative Adversarial Networks,简称GANs)是深度学习领域的一种创新结构,由Ian Goodfellow在2014年首次提出。GANs包括两个深度神经网络——一个生成器和一个判别器,它们通常以对抗的方式进行训练。 以…...

Redis性能滑坡:哈希表碰撞的不速之客【redis第二部分】
Redis性能滑坡:哈希表碰撞的不速之客 前言第一部分:Redis哈希表简介第二部分:哈希表冲突原因第三部分:Redis哈希函数第四部分:哈希表冲突的性能影响第五部分:解决冲突策略第六部分:redis是如何解…...

科技与教育的盛宴——探讨监控易在82届教装展的新机遇
在第82届中国教育装备展示会这个融合了科技与教育的盛宴上,监控易将展现其最新的教育信息化解决方案和技术创新成果。这不仅是一次产品的展示,更是一次理念、技术与需求的交流和碰撞。在这里,我们将一同探讨在科技日新月异的今天,…...
Bazzite:专为 Steam Deck 和 PC 上的 Linux 游戏打造的发行版
导读对于一个专为 Linux 游戏定制的发行版,你是否感兴趣呢?如果答案是肯定的,那么我们为你准备了绝佳选择。 Bazzite 是一个新推出的基于 Fedora 的发行版,它是为 Linux 桌面上的游戏,以及越来越火热的 Steam Deck 定…...

【MySQL】数据库数据类型
文章目录 1. 整体概要2. 数值类型(有符号) tinyint 创建表(无符号) tinyint 创建表bit类型float 类型(无符号)floatdecimal 3. 二进制类型char类型varchar类型 4. 日期时间日期时间类型 5. string 类型enum类型和set类型enum类型和set类型的查找在枚举中的查找在set中的查找 1.…...

计算机组成原理 new07 真值和机器数 无符号整数 定点整数 定点小数 $\color{red}{Δ}$
文章目录 真值和机器数 无符号整数无符号整数的定义无符号整数的特征无符号整数的表示范围无符号整数的加法无符号数的减法 有符号整数(定点整数)有符号整数的定义原码原码的特点反码反码的特点补码补码的特点快速求解n位负数补码的方法为什么补码能够多表示一个范围(重点)变形…...
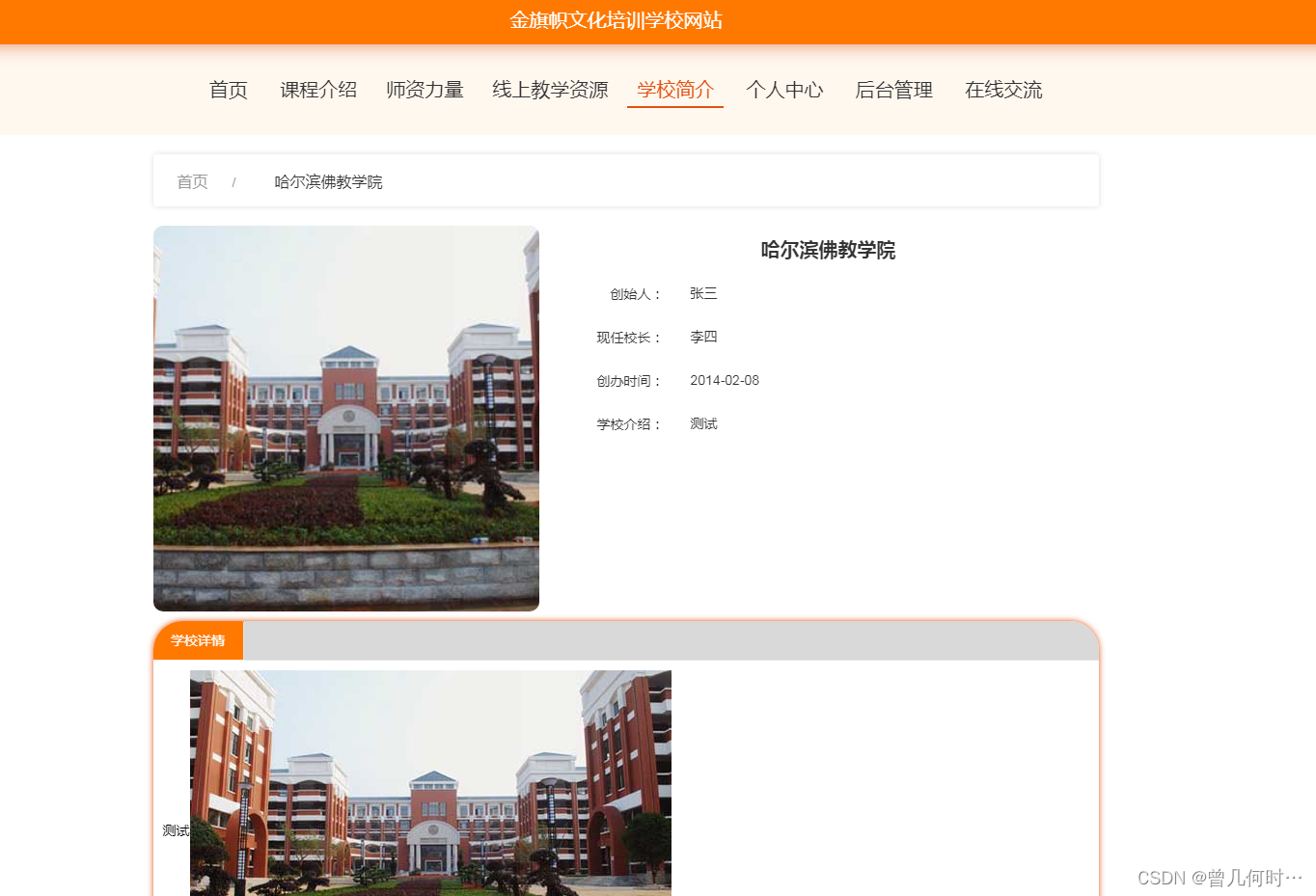
基于SSM的文化培训学校网站的设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

gitee-git使用
克隆gitee某代码仓库某分支流程 1.克隆远程gitee仓库某分支到本地 2.如果克隆gitee仓库是私有的系统会弹出弹框让你输入gitee的账户和密码 3.克隆远程分支完成 git所需命令 克隆远程仓库到本地 git clone 仓库URLgit克隆远程分支到本地 git clone -b 分支名 仓库URLgit 拉…...
)
欧拉图(Euler Graph)
这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系,下面给出定义: 通过图中所有边恰好一次且行遍所有顶点的通路称为 欧拉通路; 通过图中所有边恰好一次且行遍所有顶点的回路称为 欧拉回路; 具有欧拉回路的无向图称为 欧拉图; 具有欧拉通路但不具有欧拉回路的无向图…...

【安全体系架构】——零信任网络架构
什么是零信任网络架构? 零信任网络架构是一种网络和信息安全模型,它将传统的信任模型颠覆,不再信任内部或外部用户、设备或网络。相反,它将每个访问请求都视为不受信任,要求对每个用户、设备和流量都进行认证和授权&a…...

mybatis动态sql一对多查询
在数据库设计中,一对多关系是非常多的,例如消息通知和附件,一个消息通知中往往会包含多个附件,这种情况下使用mybatis动态sql可以很方便的查询出来。 1、数据库设计 消息表:sys_message CREATE TABLE sys_message (i…...
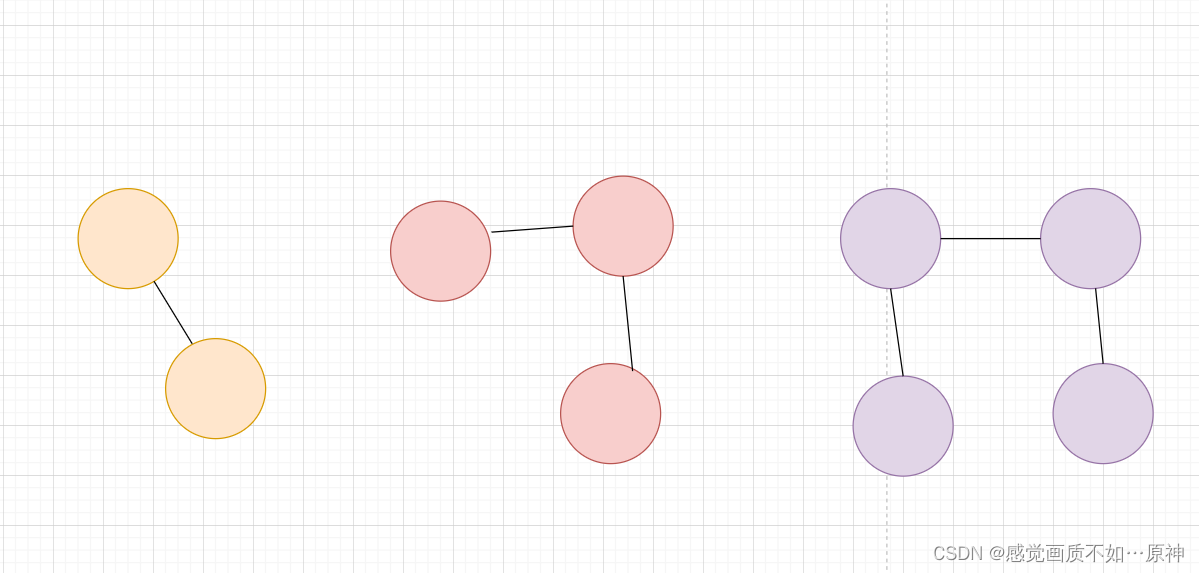
Leetcode.2316 统计无向图中无法互相到达点对数
题目链接 Leetcode.2316 统计无向图中无法互相到达点对数 rating : 1604 题目描述 给你一个整数 n n n ,表示一张 无向图 中有 n n n 个节点,编号为 0 0 0 到 n − 1 n - 1 n−1 。同时给你一个二维整数数组 e d g e s edges edges ,其…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
