《动手学深度学习 Pytorch版》 9.4 双向循环神经网络
之前的序列学习中假设的目标是在给定观测的情况下对下一个输出进行建模,然而也存在需要后文预测前文的情况。
9.4.1 隐马尔可夫模型中的动态规划
数学推导太复杂了,略。
9.4.2 双向模型
双向循环神经网络(bidirectional RNNs)添加了反向传递信息的隐藏层,以便更灵活地处理此类信息。

9.4.2.1 定义
前向和反向隐状态的更新如下:
H → t = ϕ l ( X t W x h ( f ) + H → t − 1 W h h ( f ) + b h ( f ) ) H ← t = ϕ l ( X t W x h ( b ) + H ← t − 1 W h h ( b ) + b h ( b ) ) \overrightarrow{\boldsymbol{H}}_t=\phi_l(\boldsymbol{X}_t\boldsymbol{W}^{(f)}_{xh}+\overrightarrow{\boldsymbol{H}}_{t-1}\boldsymbol{W}^{(f)}_{hh}+\boldsymbol{b}^{(f)}_h)\\ \overleftarrow{\boldsymbol{H}}_t=\phi_l(\boldsymbol{X}_t\boldsymbol{W}^{(b)}_{xh}+\overleftarrow{\boldsymbol{H}}_{t-1}\boldsymbol{W}^{(b)}_{hh}+\boldsymbol{b}^{(b)}_h) Ht=ϕl(XtWxh(f)+Ht−1Whh(f)+bh(f))Ht=ϕl(XtWxh(b)+Ht−1Whh(b)+bh(b))
参数字典:
-
H → t , H ← t ∈ R n × h \overrightarrow{\boldsymbol{H}}_t,\overleftarrow{\boldsymbol{H}}_t\in\R^{n\times h} Ht,Ht∈Rn×h 表示前向和反向隐状态
- h h h 表示隐藏单元数目
-
W x h ( f ) , W h h ( f ) , W x h ( b ) , W h h ( b ) ∈ R h × h \boldsymbol{W}^{(f)}_{xh},\boldsymbol{W}^{(f)}_{hh},\boldsymbol{W}^{(b)}_{xh},\boldsymbol{W}^{(b)}_{hh}\in\R^{h\times h} Wxh(f),Whh(f),Wxh(b),Whh(b)∈Rh×h 表示权重参数
-
b h ( f ) , b h ( b ) ∈ R 1 × h \boldsymbol{b}^{(f)}_h,\boldsymbol{b}^{(b)}_h\in\R^{1\times h} bh(f),bh(b)∈R1×h 表示偏重参数
接下来,将前向隐状态 H → t \overrightarrow{\boldsymbol{H}}_t Ht 和反向隐状态 H ← t \overleftarrow{\boldsymbol{H}}_t Ht 连接起来,获得需要送入输出层的隐状态 H t ∈ R n × 2 h \boldsymbol{H}_t\in\R^{n\times 2h} Ht∈Rn×2h。
最后,输出层计算得到的输出为:
O t = H t W h q + b q \boldsymbol{O}_t=\boldsymbol{H}_t\boldsymbol{W}_{hq}+\boldsymbol{b}_q Ot=HtWhq+bq
参数字典:
-
O t ∈ R n × q \boldsymbol{O}_t\in\R^{n\times q} Ot∈Rn×q 表示输出层输出
- q q q 表示输出单元数目
-
W h q ∈ R 2 h × q \boldsymbol{W}_{hq}\in\R^{2h\times q} Whq∈R2h×q 表示权重矩阵
-
b q ∈ R 1 × q \boldsymbol{b}_q\in\R^{1\times q} bq∈R1×q 表示偏置
9.4.2.2 模型的计算成本及其应用
在训练期间,能够利用过去和未来的数据来估计现在空缺的词;而在测试期间,只有过去的数据,因此精度将会很差。下面的实验将说明这一点。
另外,双向循环神经网络的计算速度非常慢。其主要原因是网络的前向传播需要在双向层中进行前向和后向递归,并且网络的反向传播还依赖于前向传播的结果。因此,梯度求解将有一个非常长的链。
双向层的使用在实践中非常少,并且仅仅应用于部分场合。例如,填充缺失的单词、词元注释(例如,用于命名实体识别)以及作为序列处理流水线中的一个步骤对序列进行编码(例如,用于机器翻译)。
9.4.3 双向循环神经网络的错误应用
import torch
from torch import nn
from d2l import torch as d2l
# 加载数据
batch_size, num_steps, device = 32, 35, d2l.try_gpu()
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# 通过设置“bidirective=True”来定义双向LSTM模型
vocab_size, num_hiddens, num_layers = len(vocab), 256, 2
num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers, bidirectional=True)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
# 训练模型
num_epochs, lr = 500, 1
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
perplexity 1.1, 62244.4 tokens/sec on cuda:0
time travellerererererererererererererererererererererererererer
travellerererererererererererererererererererererererererer

练习
(1)如果不同方向使用不同数量的隐藏单位, H t \boldsymbol{H}_t Ht 的形状会发生怎样的变化?
如果一个是 H → t ∈ R n × h 1 \overrightarrow{\boldsymbol{H}}_t\in\R^{n\times h_1} Ht∈Rn×h1,另一个是 H ← t ∈ R n × h 2 \overleftarrow{\boldsymbol{H}}_t\in\R^{n\times h_2} Ht∈Rn×h2 那么最后拼接出的 H t ∈ R n × ( h 1 + h 2 ) \boldsymbol{H}_t\in\R^{n\times (h_1+h_2)} Ht∈Rn×(h1+h2)。
(2)设计一个具有多个隐藏层的双向循环神经网络。
不会,略。
(3)在自然语言中一词多义很常见。例如,“bank”一词在不同的上下文“i went to the bank to deposit cash”和“i went to the bank to sit down”中有不同的含义。如何设计一个神经网络模型,使其在给定上下文序列和单词的情况下,返回该单词在此上下文中的向量表示?哪种类型的神经网络架构更适合处理一词多义?
那必然是双向循环网络。
相关文章:

《动手学深度学习 Pytorch版》 9.4 双向循环神经网络
之前的序列学习中假设的目标是在给定观测的情况下对下一个输出进行建模,然而也存在需要后文预测前文的情况。 9.4.1 隐马尔可夫模型中的动态规划 数学推导太复杂了,略。 9.4.2 双向模型 双向循环神经网络(bidirectional RNNs)…...

【Axure高保真原型】可视化图表图标
今天和粉丝们免费分享可视化图表图标原型模板,包括柱状图、条形图、环形图、散点图、水波图等常用的可视化图表图标。 【原型效果】 【原型预览】 https://axhub.im/ax9/d402c647c82f9185/#c1 【原型下载】 这个模板可以在 Axure高保真原型哦 小程序里免费下载哦…...
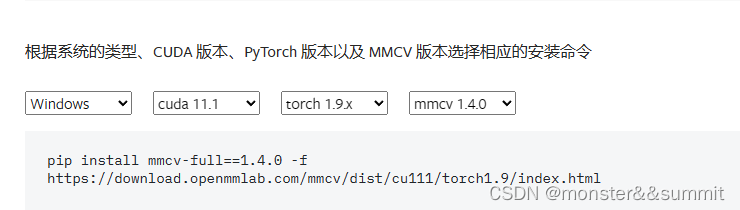
安装mmcv及GPU版本的pytorch及torchvision
一、先装GPU版本的pytorch和torchvision pip install torch1.9.1cu111 torchvision0.10.1cu111 torchaudio0.9.1 -f https://download.pytorch.org/whl/torch_stable.html注意:以上适用cuda11.1版本 如果想离线安装,就看这篇文章 二、安装mmcv 看这篇…...
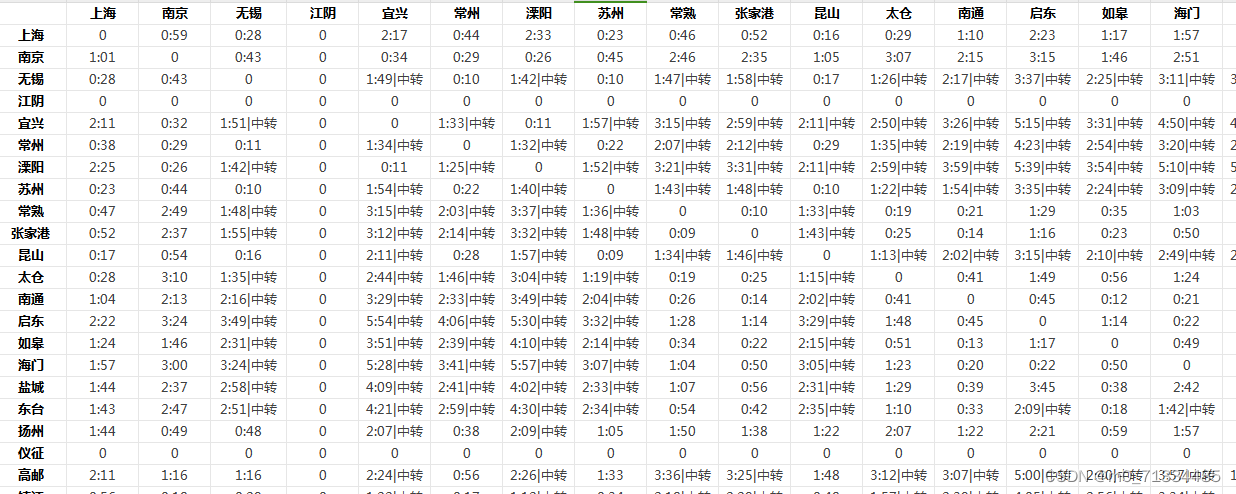
全国342个城市往返最短通勤时间(铁路)数据
全国342个城市往返最短通勤时间(铁路)数据 1、时间:采集时间是2022年 2、来源:12306 3、数据说明:数据采集12306数据,整理全国342个城市往返最短通勤时间,本数据是铁路包含动车、高铁所有路线…...

AWK语言第二版 第3章.探索性数据分析 3.1泰坦尼克号的沉没
这章也是第一版没有,第二版新增的。 3. 探索性数据分析 上一章给出了一些个人使用的小脚本,通常是特制或专用的。在本章中,我们还会展示Awk在现实中的典型使用场景:使用Awk和其他工具来非正式地探索一些真实的数据,目…...
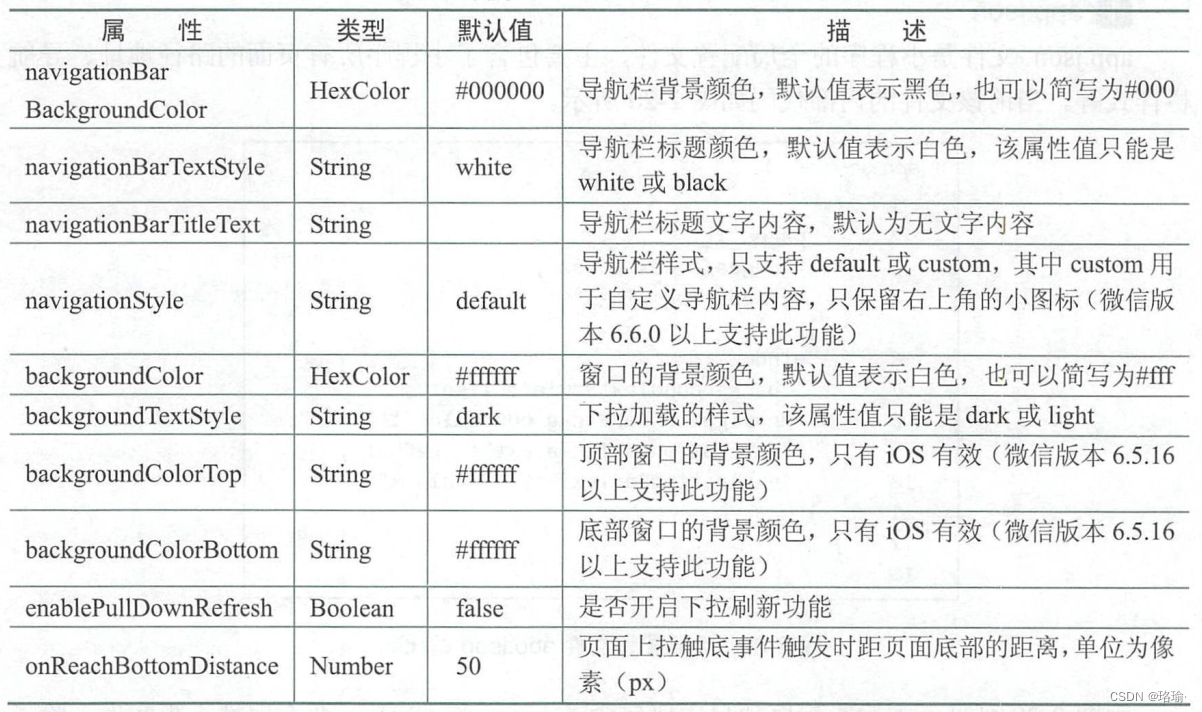
微信小程序设计之主体文件app-json-window
一、新建一个项目 首先,下载微信小程序开发工具,具体下载方式可以参考文章《微信小程序开发者工具下载》。 然后,注册小程序账号,具体注册方法,可以参考文章《微信小程序个人账号申请和配置详细教程》。 在得到了测…...

WebDAV之π-Disk派盘 + 密码键盘
密码键盘是一款密码管理器,可以存储和管理需要受保护的数据。为方便日常使用,同时也是一款安全输入法,帮您安全便捷地填写账号密码、通用内容、卡包信息。 密码键盘使用军事级的 PBKDF2 有损加密算法保护您的根密码,使用军事级的 AES 加密算法保护您的存储数据。云端再额外…...

LeetCode讲解篇之77. 组合
文章目录 题目描述题解思路题解代码 题目描述 题解思路 遍历nums,让当前数字添加到结果前缀中,递归调用,直到前缀的长度为k,然后将前缀添加到结果集 题解代码 func combine(n int, k int) [][]int {var nums make([]int, n)fo…...

【openwrt学习笔记】Dying Gasp功能和pstore功能的配置(高通 ipq95xx)
目录 一、Dying Gasp信号1.1 概念1.2 实现原理 二、pstore 功能2.1 概念2.2 实现原理 三、openwrt中开启pstore功能3.1 软硬件参数3.2 各文件修改3.2.1 defconfig3.2.2 dts(ipq9574-default-memory.dtsi)3.2.3 fs/pstore/ram.c 四、测试4.1 挂载4.2 触发命令和效果 参考资料&am…...

使用RestSharp和C#编写程序
以下是一个使用RestSharp和C#编写的爬虫程序,用于爬取www.zhihu.com上的视频。此程序使用了https://www.duoip.cn/get_proxy来获取代理IP。 using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks…...

Leetcode 2911. Minimum Changes to Make K Semi-palindromes
Leetcode 2911. Minimum Changes to Make K Semi-palindromes 1. 解题思路2. 代码实现 题目链接:2911. Minimum Changes to Make K Semi-palindromes 1. 解题思路 这一题属实也是把我坑惨了…… 坦率地说,这道题本身并没有啥难度,但是坑爹…...
Node学习笔记之包管理工具
一、概念介绍 1.1 包是什么 『包』英文单词是package ,代表了一组特定功能的源码集合 1.2 包管理工具 管理『包』的应用软件,可以对「包」进行 下载安装 , 更新 , 删除 , 上传 等操作 借助包管理工具,可…...
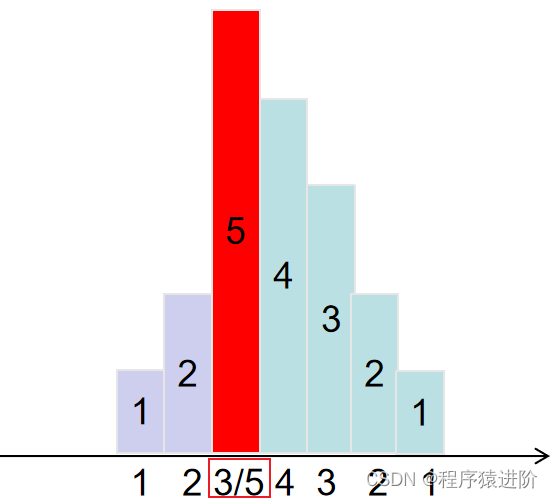
分发糖果[困难]
优质博文:IT-BLOG-CN 一、题目 n个孩子站成一排。给你一个整数数组ratings表示每个孩子的评分。你需要按照以下要求,给这些孩子分发糖果: 【1】每个孩子至少分配到1个糖果。 【2】相邻两个孩子评分更高的孩子会获得更多的糖果。 请你给每个孩…...

Java验证邮箱格式是否正确的正则表达式
Java验证邮箱格式是否正确的正则表达式 import java.util.regex.Pattern;public class EmailUtil {final static Pattern partern Pattern.compile("[a-zA-Z0-9][\\.]{0,1}[a-zA-Z0-9][a-zA-Z0-9]\\.[a-zA-Z]");/*** 验证输入的邮箱格式是否符合* param email* ret…...

快速排序原理JAVA和Scala实现-函数式编程的简洁演示
快速排序原理JAVA和Scala实现-函数式编程的简洁演示 目录 快速排序原理JAVA和Scala实现-函数式编程的简洁演示 C语言快速排序实现 Java 快速排序实现 Scala 快速排序实现 本文章向大家介绍快速排序原理JAVA和Scala实现-函数式编程的简洁演示,主要内容包括C语言…...
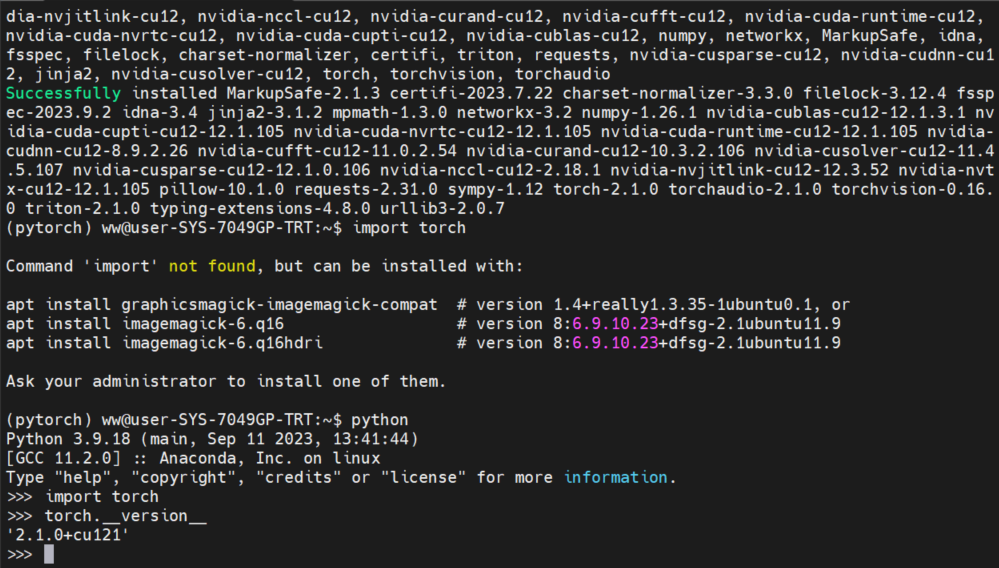
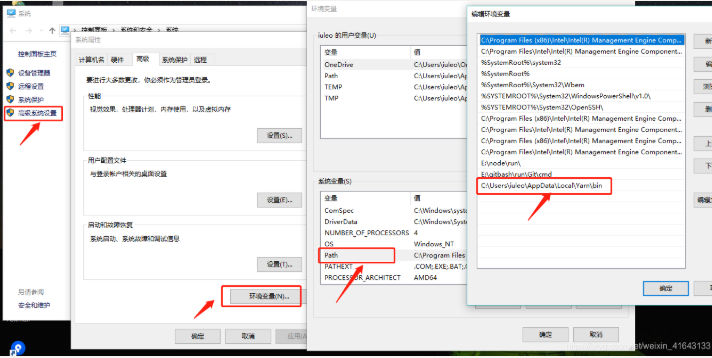
如何在linux服务器上安装Anaconda与pytorch
如何在linux服务器上安装Anaconda与pytorch 1,安装anaconda1.1 下载anaconda安装包1.2 安装anaconda1.3 设计环境变量1.4 安装完成验证 2 Anaconda安装pytorch2.1 创建虚拟环境2.2 查看现存环境2.3 激活环境2.4 选择合适的pytorch版本下载2.5 检测是否安装成功&…...
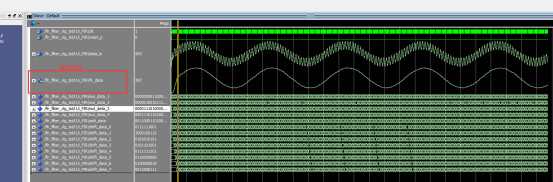
FPGA设计FIR滤波器低通滤波器,代码及视频
名称:FIR滤波器低通滤波器 软件:Quartus 语言:Verilog/VHDL 本资源含有verilog及VHDL两种语言设计的工程,每个工程均可实现以下FIR滤波器的功能。 代码功能: 设计一个8阶FIR滤波器(低通滤波器ÿ…...
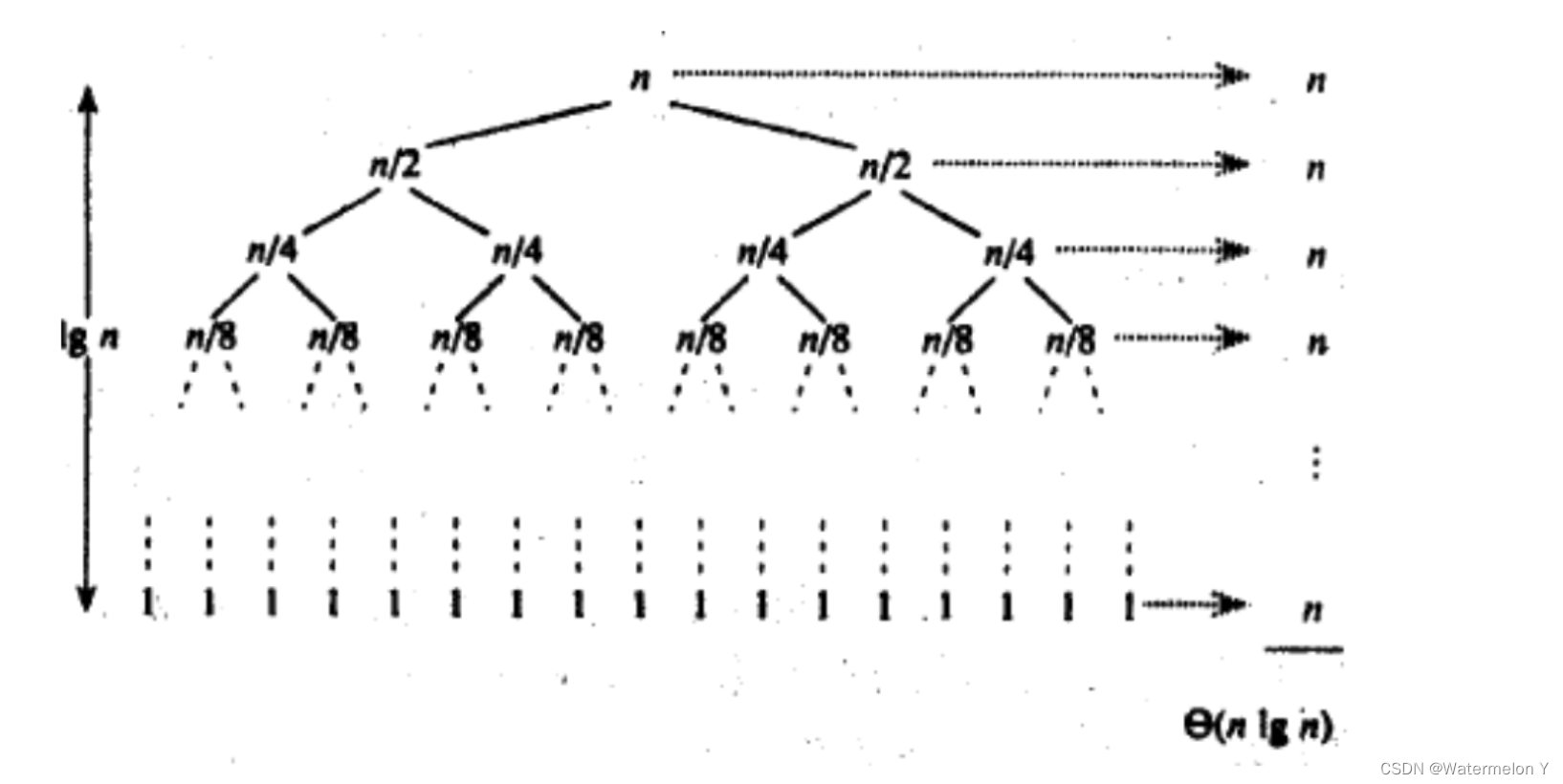
【数据结构】排序--快速排序
目录 一 概念 二 快速排序的实现 1. hoare版本 (1)代码实现 (2)单趟排序图解 (3) 递归实现图解 (4)细节控制 (5)时间复杂度 (6)三数取中优化 2 挖坑法 (1)代码实现 (2)单趟图解 3 前后指针法 (1) 代码实现 (2) 单趟图解 4 优化子区间 5 非递归快速排序 …...
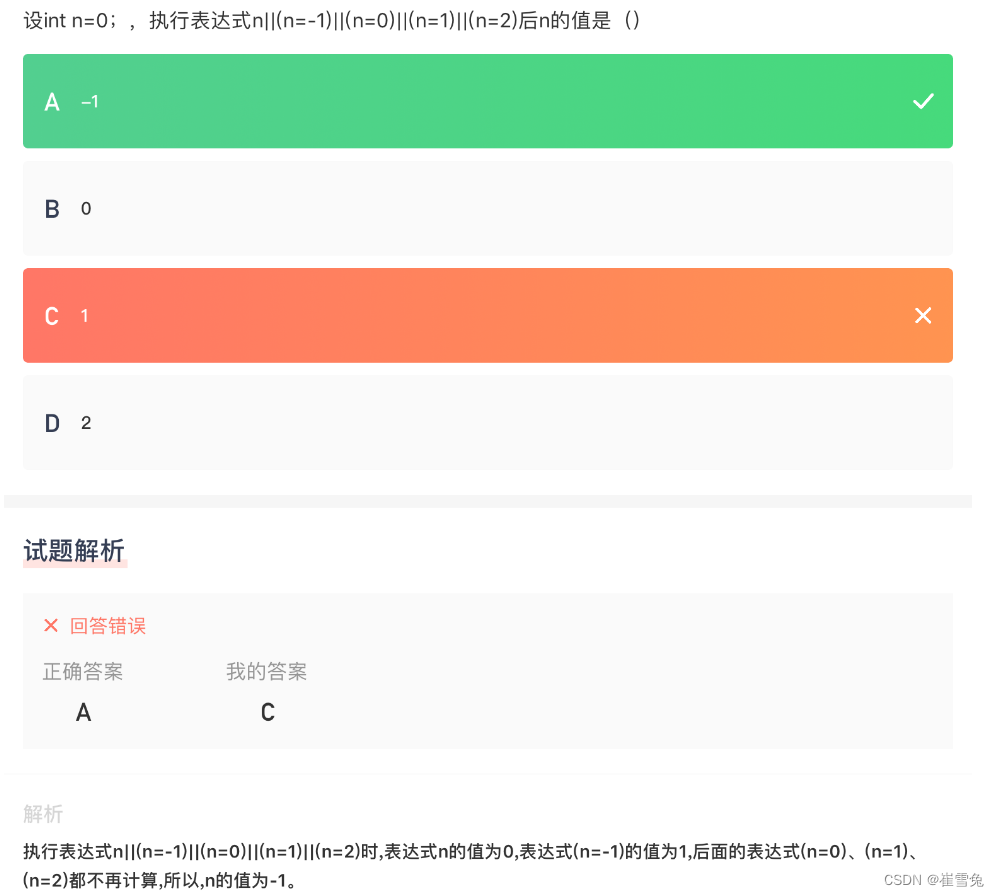
【试题040】多个逻辑或例题2
1.题目:设int n0;,执行表达式n ||(n-1) ||(n0)||(n1)||(n2)后n的值是 ? 2.代码解析: 逻辑或 || 运算符是一个短路运算符,它从左到右依次计算表达式,如果遇到一个为真(非零)的值&am…...

自然语言处理---Self Attention自注意力机制
Self-attention介绍 Self-attention是一种特殊的attention,是应用在transformer中最重要的结构之一。attention机制,它能够帮助找到子序列和全局的attention的关系,也就是找到权重值wi。Self-attention相对于attention的变化,其实…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...
