【C++】哈希应用——海量数据面试题
哈希应用——海量数据面试题
- 一、位图应用
- 1、给定100亿个整数,设计算法找到只出现一次的整数?
- 2、给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
- (1)用一个位图(512MB)
- (2)用两个位图(1GB)
- 3、位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
- 二、哈希切割
- 三、布隆过滤器
- 1、给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法
- 2、如何扩展BloomFilter使得它支持删除元素的操作
一、位图应用
1、给定100亿个整数,设计算法找到只出现一次的整数?
我们描述状态有三种,分别是:
1、出现0次
2、出现1次
3、出现2次及以上
我们了解到,如果只有一个位图,那么状态就只有0和1两种状态,所以我们如果想要描述上面的三种状态的话,那么我们就需要开辟两个位图进行存储这三种情况,其第一个位和第二个位的组合进行分析出这三种情况。
这三种情况分别是:00->01->10,此时当我们读取到重复的整数时,就可以让其对应的两个位按照00→01→10的顺序进行变化,最后状态是01的整数就是只出现一次的整数。
#include<iostream>
#include<vector>
#include<assert.h>
#include<bitset>
using namespace std;int main()
{// 此处应该从文件中读取100亿个整数vector<int> v{ 12, 8, 13, 2, 8, 1, 2, 3, 3, 12, 43, 77 };// 堆上申请空间// 申请两个位图bitset<4294967295>* bs1 = new bitset<4294967295>;bitset<4294967295>* bs2 = new bitset<4294967295>;for (auto e : v){if (!bs1->test(e) && !bs2->test(e)) // 00->01{bs2->set(e);}else if (!bs1->test(e) && bs2->test(e)) // 01->10{bs1->set(e);bs2->reset(e);}else if (bs1->test(e) && !bs2->test(e)) // 10->10{// 不做任何处理}else{assert(false);}}for (size_t i = 0; i < 4294967295; i++){// 打印01if (!bs1->test(i) && bs2->test(i)){cout << i << " ";}}cout << endl;return 0;
}
注意点:如果我们存储100亿个整数的话,在堆中需要申请大约40个G的空间,这个空间是非常大的,而我们利用位图来解决这个问题的时候,我们就只需要512MB,也就是代码中的4294967295,两个位图才只需要1个G的空间。
2、给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
(1)用一个位图(512MB)
方法是依次读取文件中的整数的值,将其映射到一个位图中,再读取另一个文件中的所有整数,判断在不在位图中,在就是交集,不在就不是交集。
(2)用两个位图(1GB)
依次读取第一个文件中的所有整数,将其映射到位图1。依次读取另一个文件中的所有整数,将其映射到位图2。将位图1和位图2进行与操作,结果存储在位图1中,此时位图1当中映射的整数就是两个文件的交集。
3、位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
这个与第一道题目大差不差,我们直接进行更改一下就可以进行书写了:
#include<iostream>
#include<vector>
#include<assert.h>
#include<bitset>
using namespace std;int main()
{// 此处应该从文件中读取100亿个整数vector<int> v{ 12, 8, 13, 2, 8, 1, 2, 3, 3, 12, 43, 77 };// 堆上申请空间// 申请两个位图bitset<4294967295>* bs1 = new bitset<4294967295>;bitset<4294967295>* bs2 = new bitset<4294967295>;for (auto e : v){if (!bs1->test(e) && !bs2->test(e)) // 00->01{bs2->set(e);}else if (!bs1->test(e) && bs2->test(e)) // 01->10{bs1->set(e);bs2->reset(e);}else if (bs1->test(e) && !bs2->test(e)) // 10->10{// 不做任何处理}else{assert(false);}}for (size_t i = 0; i < 4294967295; i++){// 打印01和10if ((!bs1->test(i) && bs2->test(i)) || ((bs1->test(i) && !(bs2->test(i))))){cout << i << " ";}}cout << endl;return 0;
}二、哈希切割
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址?与上题条件相同,如何找到top K的IP?如何直接用Linux系统命令实现?
1、我们将这个log file叫做A文件,由于A文件的大小超过100G,这里可以考虑将A文件切分成200个小文件。
2、在切分时选择一个哈希函数进行哈希切分,通过哈希函数将A文件中的每个IP地址转换成一个整型 i(0 ≤ i ≤ 199),然后将这个IP地址写入到小文件Ai当中。
3、由于哈希切分时使用的是同一个哈希函数,因此相同的IP地址计算出的 i i值是相同的,最终这些相同的IP地址就会进入到同一个Ai小文件当中。
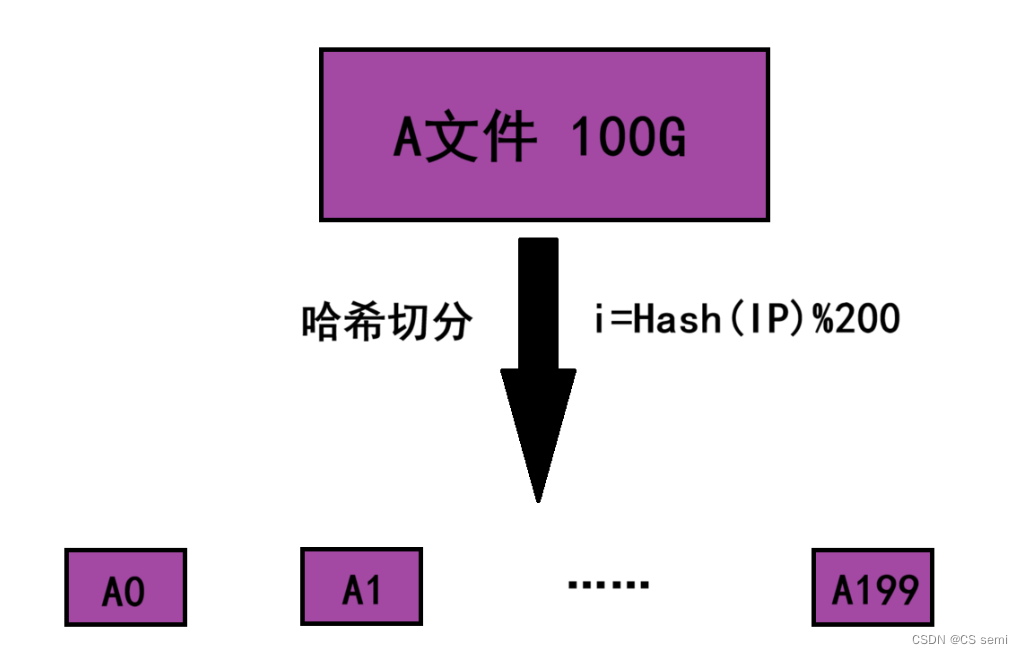
经过哈希切分后得到的这些小文件,理论上就能够加载到内存当中了,如果个别小文件仍然太大那可以对其再进行一次哈希切分,总之让最后切分出来的小文件能够加载到内存。
我们用sort log_file | uniq -c | sort -nrk1,1 | head -K命令选取出现次数top K的IP地址。
利用sort进行排序。
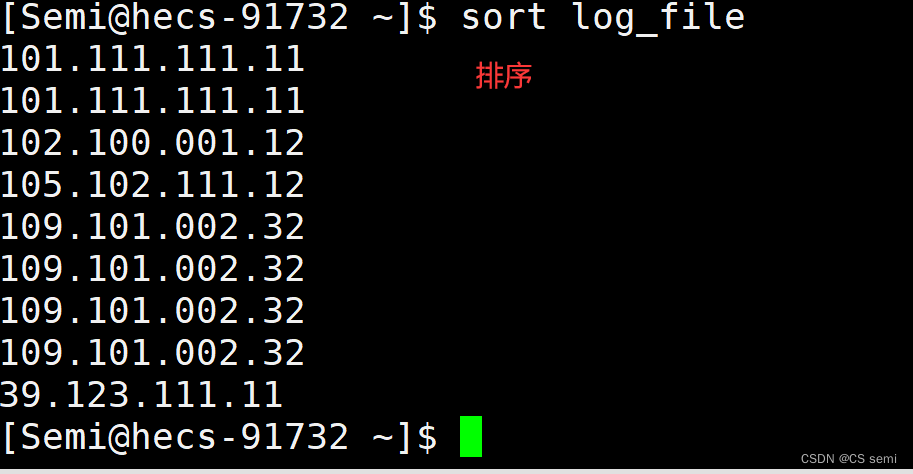
利用uniq统计出现次数。
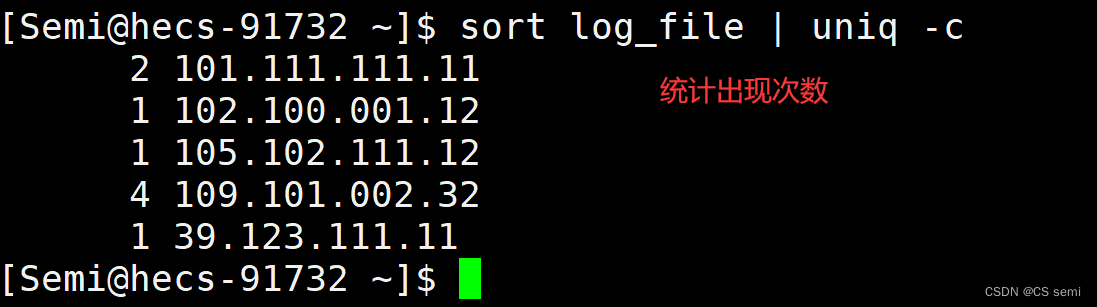
-nrk1进行反向排序。
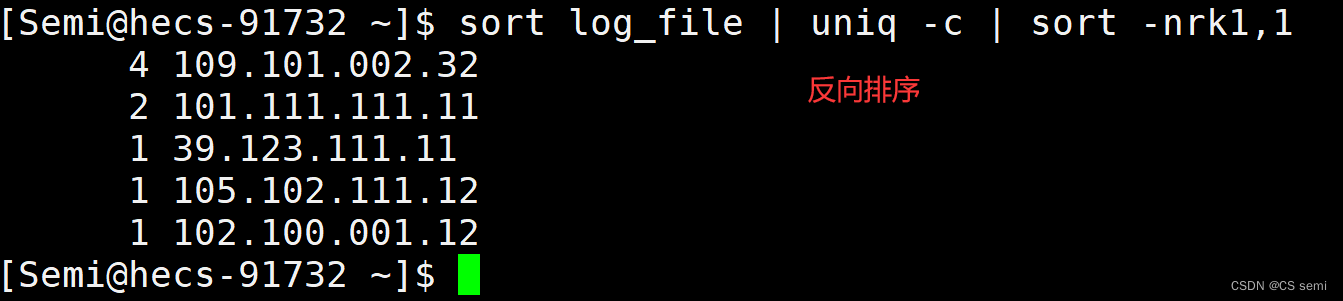
前两个。

三、布隆过滤器
1、给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法
先读取其中一个文件当中的query,将其全部映射到一个布隆过滤器当中。然后读取另一个文件当中的query,依次判断每个query是否在布隆过滤器当中,如果在则是交集,不在则不是交集。
2、如何扩展BloomFilter使得它支持删除元素的操作
布隆过滤器不能直接支持删除工作,因为在删除一个元素时,可能会影响其他元素。
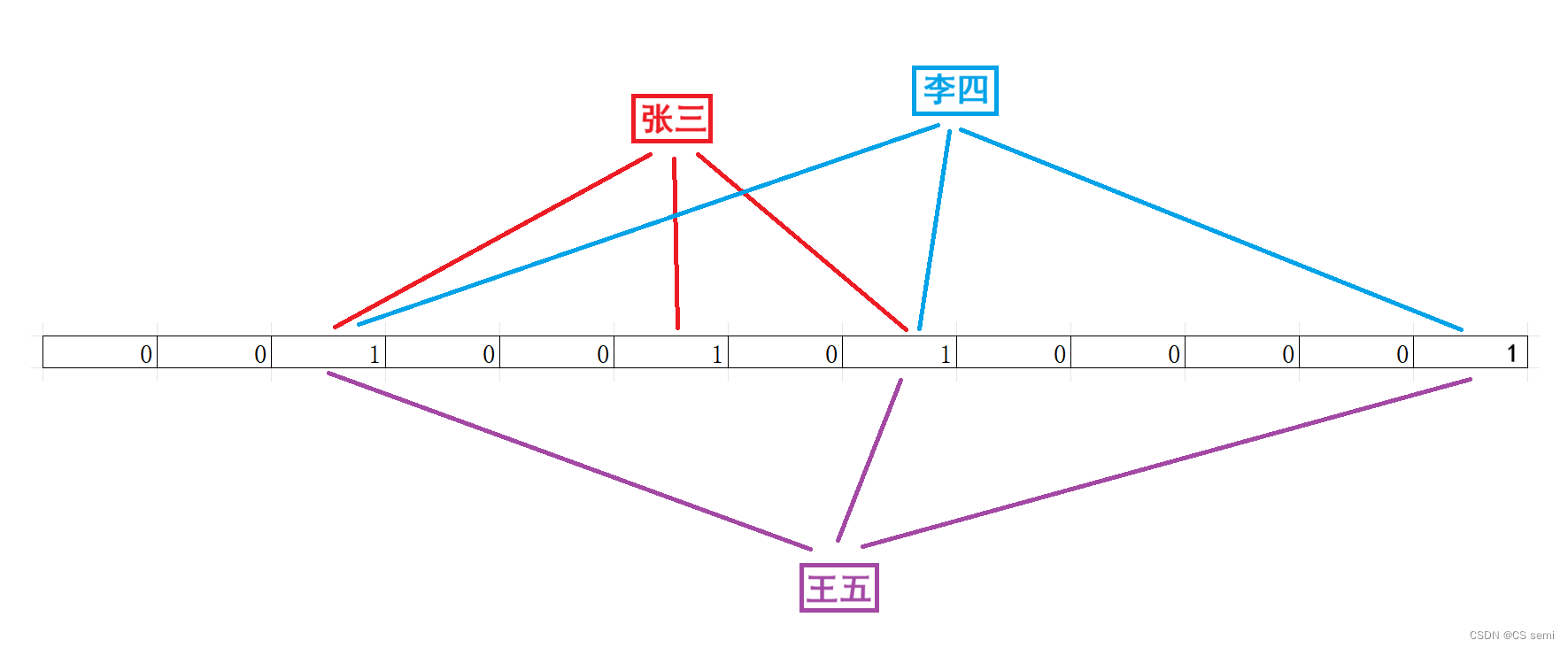
如上图,如果我们删除“李四”这个数据的话,那么三个1都要置0,则导致张三有俩置0了!那张三的数据岂不是很奇怪?
一种支持删除的方法:将布隆过滤器中的每个比特位扩展成一个小的计数器,插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一,删除元素时,给k个计数器减一,通过多占用几倍存储空间的代价来增加删除操作。
相关文章:

【C++】哈希应用——海量数据面试题
哈希应用——海量数据面试题 一、位图应用1、给定100亿个整数,设计算法找到只出现一次的整数?2、给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?(1)用一个位图…...
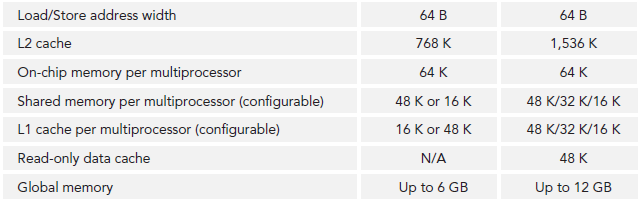
CUDA学习笔记(五)GPU架构
本篇博文转载于https://www.cnblogs.com/1024incn/tag/CUDA/,仅用于学习。 GPU架构 SM(Streaming Multiprocessors)是GPU架构中非常重要的部分,GPU硬件的并行性就是由SM决定的。 以Fermi架构为例,其包含以下主要组成…...
逻辑漏洞详解
原理: 没有固定的概念,一般都是不符合常识的情况。比如任意用户注册,短信炸弹,占用资源,交易支付、密码修改、密码找回、越权修改、越权查询、突破限制。 根据实际业务逻辑进行比对,购物的可以根据数量&a…...
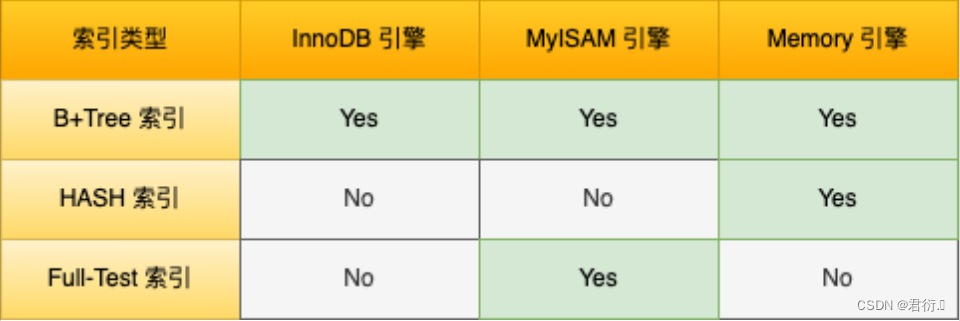
MySQL——八、MySQL索引视图
MySQL 一、视图1、什么是视图2、为什么需要视图3、视图的作用和优点4、创建视图5、视图使用规则6、修改视图7、删除视图 二、索引1、什么是索引2、索引优缺点3、索引分类4、索引的设计原则5、创建索引5.1 创建表是创建索引5.2 create index5.3 ALTER TABLE 6、删除索引7、MySQL…...
)
力扣100097. 合法分组的最少组数(哈希+贪心)
题目描述: 给你一个长度为 n 下标从 0 开始的整数数组 nums 。 我们想将下标进行分组,使得 [0, n - 1] 内所有下标 i 都 恰好 被分到其中一组。 如果以下条件成立,我们说这个分组方案是合法的: 对于每个组 g ,同一…...
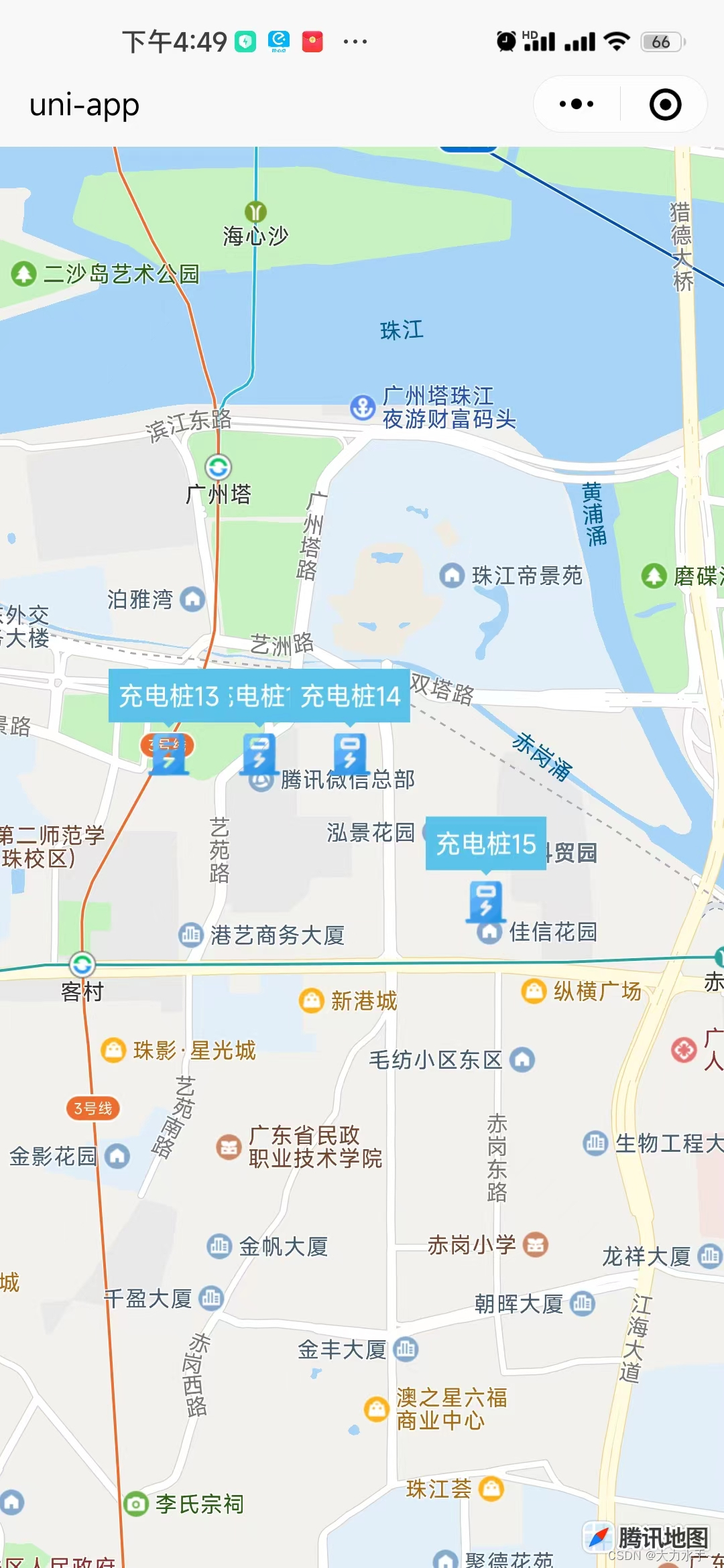
uniapp map地图实现marker聚合点,并点击marker触发事件
1.uniapp官方文档说明 2.关键代码片段 // 仅调用初始化,才会触发 on.("markerClusterCreate", (e) > {})this._mapContext.initMarkerCluster({enableDefaultStyle: false, // 是否使用默认样式zoomOnClick: true, // 点击聚合的点,是否…...
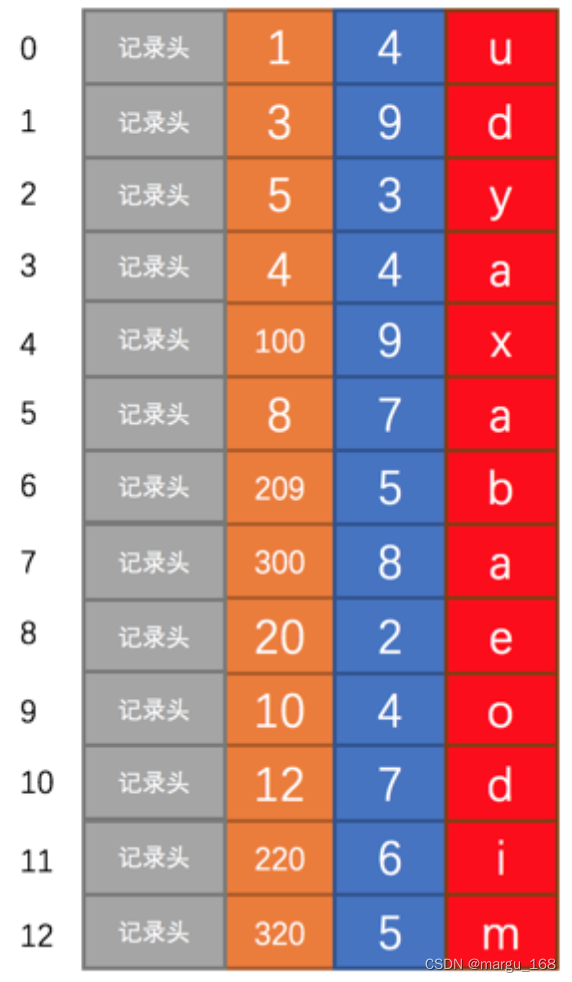
【Mysql】Mysql中的B+树索引(六)
概述 从上一章节我们了解到InnoDB 的数据页都是由7个部分组成,然后各个数据页之间可以组成一个双向链表 ,而每个数据页中的记录会按照主键值从小到大的顺序组成一个单向链表 ,每个数据页都会为存储在它里边儿的记录生成一个页目录 ÿ…...
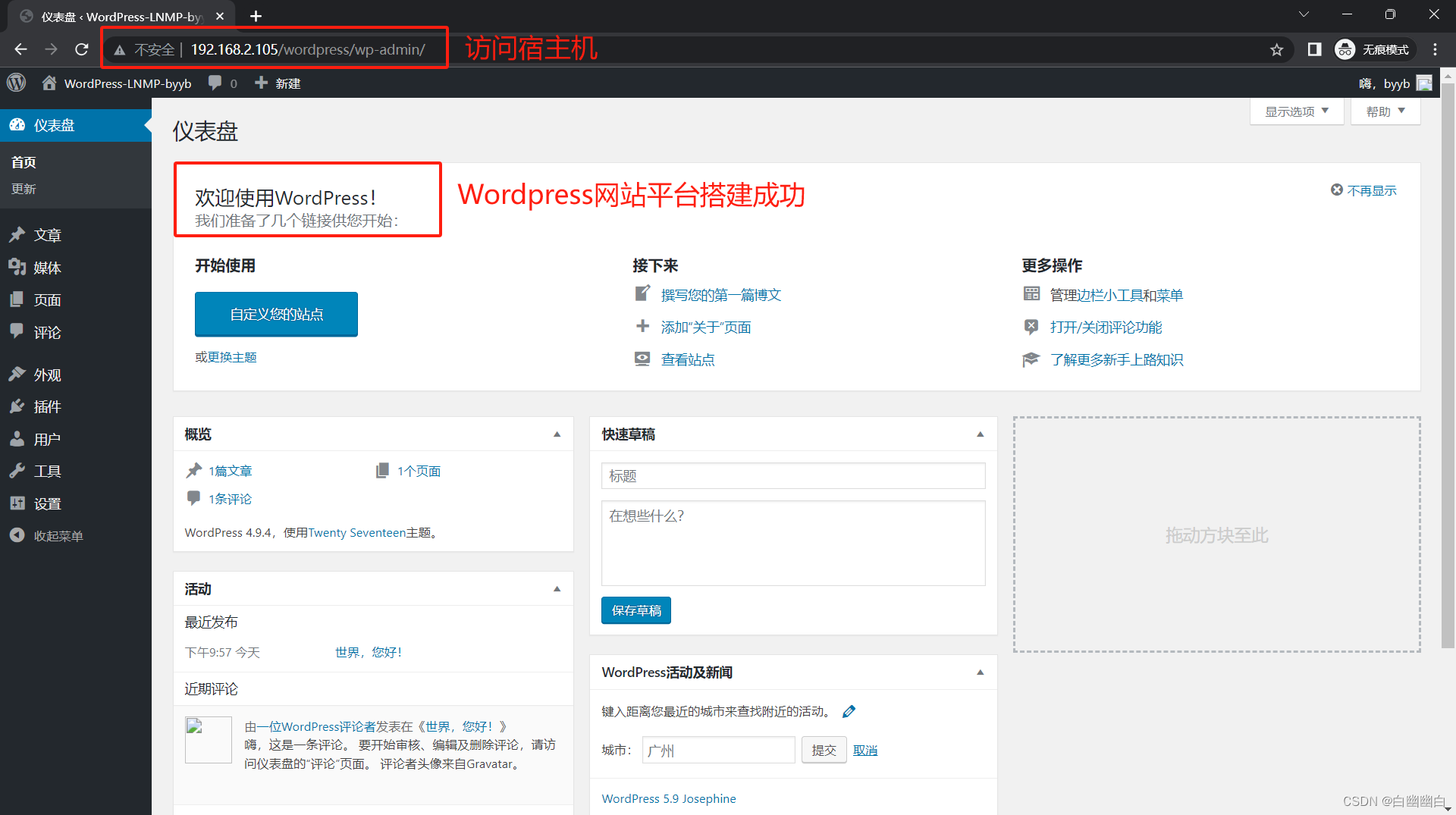
【Dockerfile镜像实战】构建LNMP环境并运行Wordpress网站平台
这里写目录标题 一、项目背景和要求二、项目环境三、部署过程1)创建自定义网络2)部署NginxStep1 创建工作目录并上传相关软件包Step2 编写Dockerfile文件Step3 编写配置文件nginx.confStep4 创建nginx镜像Step5 运行容器 3)部署MysqlStep1 创…...

【工具】利用ffmpeg将网页中的.m3u8视频文件转化为.mp4格式
目录 0.环境 1.背景 2.前提 3.详细描述 1)在网站上找到你想下载的视频的.m3u8链接 2)打开命令行,用ffmpeg命令进行转化 3)过程&结果截图 0.环境 windows64 ffmpeg 1.背景 网页上有个.m3u8格式的视频文件,…...

Git简洁安装方式和使用方式【附安装包资源,Git基础操作,如拉取项目、上传代码、拉取代码】
文章目录 软件安装包安装步骤常用使用方式注意拉取项目上传代码或文件选择文件添加到本地Git存储库的缓存区将缓存区的更改提交到本地Git存储库,并设置提交信息将本地Git存储库的更新推送到远程Git仓库中上传示例拉取别人所上传的代码 常见问题上传代码失败…...
【29】c++设计模式——>策略模式
策略模式 C中的策略模式(Strategy Pattern)是一种行为型设计模式,它允许在运行时选择算法的行为。策略模式通过将算法封装成独立的类,并且使它们可以互相替换,从而使得算法的变化独立于使用算法的客户端。 策略模式通…...
2023Jenkins连接k8s
首先配置k8s config文件 1.方式获取k8s密钥 cat .kube/config 2.导出方式或者密钥 kubectl config view --raw > k8s-config-admin pipeline {agent {kubernetes {yaml apiVersion: v1kind: Podmetadata:labels:some-label: devopsspec:containers:- name: dockerimage: d…...
SpringBoot 入门 参数接收 必传参数 数组 集合 时间接收
接口声明 RestController //表示该类为请求处理类public class HttpDeal {RequestMapping("/login")//这个方法处理哪一个地址过来的请求public String hello(){return "返回给浏览器";}}接收参数 RequestMapping("/login")public String logi…...

【Qt之JSON文件】QJsonDocument、QJsonObject、QJsonArray等类介绍及使用
Qt之JSON相关类介绍 QJsonDocument常用函数枚举类型 QJsonDocument::DataValidation枚举类型 QJsonDocument::JsonFormat构造函数静态函数成员函数示例 QJsonObject常用函数构造函数:成员函数: QJsonObject 与 QVariantMap 相互转换 QJsonArray常用函数构…...

阿里云今年有双十一活动吗?不好说
阿里云今年有双十一活动吗?不好说,因为去年就没有。阿里云双11优惠活动是一项大型的促销活动,每年都有,但是去年没有双十一活动,不知道今年2023年阿里云是否有双11优惠活动。但是阿里云百科aliyunbaike.com猜想&#x…...

【驱动开发】创建设备节点、ioctl函数的使用
一、控制三盏灯的亮灭 头文件: #ifndef __HEAD_H__ #define __HEAD_H__ typedef struct{unsigned int MODER;unsigned int OTYPER;unsigned int OSPEEDR;unsigned int PUPDR;unsigned int IDR;unsigned int ODR; }gpio_t; #define PHY_LED1_ADDR 0X50006000 #def…...
Tomcat启动控制台乱码问题
修改Tomcat/conf/logging.properties...

学习周总结
http://t.csdnimg.cn/DKki2 http://t.csdnimg.cn/NvudJ 项目进度 做了大概的主界面,然后做了一个客户端和服务端的分离,实现了在客户端发送的信息,在服务端能收到;客户端和服务端的制作是我之前有写的一个http://t.csdnimg.cn/…...

如何在不恢复出厂设置的情况下解锁 Android 手机密码?
当您忘记 Android 手机的密码时,可能会有压力,尤其是当您不想恢复出厂设置并删除所有数据时。但是,有一些方法可以在不诉诸如此激烈的步骤的情况下解锁手机。我们将在这篇文章中教您如何在不恢复出厂设置的情况下解锁 Android 手机密码。我们…...

移动设备管理对企业IT 安全的增强
移动设备管理 (MDM) 是通过定义策略和部署安全控制(如移动应用程序管理、移动内容管理和条件 Exchange 访问)来管理移动设备的过程。 完整的MDM解决方案可以管理在Android,iOS,Windows,macOS&a…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
