三维模型表面积计算方法
【版权声明】
本文为博主原创文章,未经博主允许严禁转载,我们会定期进行侵权检索。
更多算法总结请关注我的博客:https://blog.csdn.net/suiyingy,或”乐乐感知学堂“公众号。
本文章来自于专栏《Python三维模型处理基础》的系列文章,专栏地址为:https://blog.csdn.net/suiyingy/category_12462636.html。
在当今数字化时代,三维模型已经广泛应用于各个领域,如游戏开发、建筑设计、工程制图等。了解三维模型的表面积以及其计算方法,对于模型的几何特征分析和后续处理具有重要意义。本篇博文将带您深入了解三维模型表面积的定义、作用以及计算方法。
1 表面积定义
三维模型表面积是指模型所有外部表面的总面积。在数学上,它可以被视为一个多边形网格的组合,由许多个平面三角形组成。每个三角形都有自己的面积,将它们相加即可得到整个模型的表面积。
2 表面积作用
几何特征分析:表面积可以用于对三维模型的几何特征进行分析和描述。通过表面积,我们可以了解模型的大小、形状以及精细程度,从而为后续的评估和改进工作提供基础数据。
光照和渲染:在计算机图形学中,光照和渲染是模拟真实世界的重要步骤。表面积决定了模型的各个部分可以接收到多少光线,从而影响最终的视觉效果。计算表面积有助于优化渲染过程,提高图像质量和真实感。
物理仿真:在物理仿真中,表面积对于计算模型的质量、密度以及碰撞检测等方面非常重要。通过对表面积的计算,可以更准确地模拟模型的物理行为,提高仿真的准确性和真实度。
此外,上一节介绍的三维模型顶点法向量计算过程中加权求和的权重也由表面积来决定。
3 计算方法
计算三维模型表面积的方法有多种,这里介绍两种常用的方法,即多边形网格法和曲面拟合法。
多边形网格法的步骤为:
(1)首先,将三维模型表示为一个由多个小三角形组成的多边形网格。
(2)计算每个三角形的面积,可以使用海伦公式或矢量运算等方法。
(3)将所有三角形的面积相加,得到整个模型的表面积。
曲面拟合法的步骤为:
(1)首先,将三维模型表面离散化为一系列点云。
(2)使用曲面拟合算法,如Bezier曲线或B样条曲线,将点云拟合成光滑的曲面。
(3)计算拟合曲面的表面积。
需要注意的是,计算三维模型表面积的精确度与离散化程度相关。较为密集的网格或点云将提供更准确的结果,但也会增加计算复杂度和存储需求。
4 python示例程序
4.1 单个三角面
这里我们仍然采用trimesh和open3d来计算三维模型的表面积。我们首先以单个三角面为例,假设顶点坐标分别为[[0.0, 0.0, 1.0], [3.0, 0.0, 1.0], [0.0, 4.0, 1.0]]。显然,这是一个直角三角形,其面积为1/2 * 3 * 4 = 6。
Trimesh计算三维模型表面积的函数为mesh.area,上述三角面的计算结果为6.0,与预期理论结果一致。关键程序如下所示。
mesh = trimesh.Trimesh(vertices=vertices, faces=faces)
print('area result: ', mesh.area)Open3d计算三维模型表面积的函数为open3d.geometry.TriangleMesh.get_surface_area (Python method, in open3d.geometry.TriangleMesh),上述三角面的计算结果为6.0,与预期理论结果一致。关键程序如下所示。
mesh.vertices = o3d.utility.Vector3dVector(vertices)
mesh.triangles = o3d.utility.Vector3iVector(faces)
print('area result: ', mesh.get_surface_area())4.2 三棱柱表面积
假设三棱柱顶点和三角网格面分别为[[0.0, 0.0, 0.0], [3.0, 0.0, 0.0], [0.0, 4.0, 0.0], [0.0, 0.0, 5.0], [3.0, 0.0, 5.0], [0.0, 4.0, 5.0]]、[[1, 3, 2], [2, 3, 5], [5, 3, 6], [1, 4, 3], [3, 4, 6], [1, 2, 4], [2, 5, 4], [4, 5, 6]]。三棱柱示意图如下所示,底面是一个直角三角形。上下底面的面积均为6.0,三个侧面的面积依次为15.0、20.0、25.0,因此总面积为72.0。

图1 三棱柱模型
Trimesh和open3d相应表面积计算结果均为72.0。之前的博文介绍提到,三维模型的体积计算结果受到顶点顺序和封闭性影响。而三维模型的表面积则不受顶点顺序影响,并且仅计算三角网格的面积之和,孔洞不会自动补全或参与计算。
Trimesh可通过mesh.area_faces来获取各个三角面的面积,例如上述三棱柱对应的area_faces的计算结果为[ 6. 12.5 12.5 10. 10. 7.5 7.5 6. ]。
上述计算结果的详细Python示例程序下载地址为“https://download.csdn.net/download/suiyingy/88457956”,或者在”乐乐感知学堂“內回复”3d处理基础“即可。
此外,Cloud Compare也提供三维模型的表面积计算方法,其计算步骤为:首先加载并选中mesh模型,然后依次点击Edit->Mesh->Measure surface,如下图所示。

图2 Could Compare表面积计算过程
表面积计算结果会显示在下方提示区域,如下图所示。三棱柱表面积计算结果为S=72,与上述手动计算结果一致。
图3 Could Compare表面积计算结果
本篇博文介绍了三维模型表面积的定义、作用以及常用的计算方法。了解三维模型的表面积对于模型分析、渲染和仿真具有重要意义。通过计算表面积,我们可以更深入地理解三维模型的几何特征,并为相关领域的应用提供有力支持。希望本文能够帮助读者更好地理解和应用三维模型表面积的知识。
【版权声明】
本文为博主原创文章,未经博主允许严禁转载,我们会定期进行侵权检索。
更多算法总结请关注我的博客:https://blog.csdn.net/suiyingy,或”乐乐感知学堂“公众号。
本文章来自于专栏《Python三维模型处理基础》的系列文章,专栏地址为:https://blog.csdn.net/suiyingy/category_12462636.html。
相关文章:

三维模型表面积计算方法
【版权声明】 本文为博主原创文章,未经博主允许严禁转载,我们会定期进行侵权检索。 更多算法总结请关注我的博客:https://blog.csdn.net/suiyingy,或”乐乐感知学堂“公众号。 本文章来自于专栏《Python三维模型处理基础》的系列文…...
unity脚本_力 c#
创建一个脚本 将代码挂载到物体上 取消物体的重力 运行即向z轴运动 加力之后 是否停止是由阻力影响 如果阻力为零 则会一直运动 如果希望就算有阻力也让物体一直动就将加力代码放在Update函数里 using UnityEngine; public class Power : MonoBehaviour{ Rigidbody rigidBo…...

LeetCode 面试题 10.05. 稀疏数组搜索
文章目录 一、题目二、C# 题解 一、题目 稀疏数组搜索。有个排好序的字符串数组,其中散布着一些空字符串,编写一种方法,找出给定字符串的位置。 示例1: 输入: words [“at”, “”, “”, “”, “ball”, “”, “”, “car”, “”, “”…...

分类预测 | MATLAB实现基于BiLSTM-AdaBoost双向长短期记忆网络结合AdaBoost多输入分类预测
分类预测 | MATLAB实现基于BiLSTM-AdaBoost双向长短期记忆网络结合AdaBoost多输入分类预测 目录 分类预测 | MATLAB实现基于BiLSTM-AdaBoost双向长短期记忆网络结合AdaBoost多输入分类预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.MATLAB实现基于BiLSTM-…...

Sobel算子详解及例程
Sobel算子是一种经典的边缘检测算子,被广泛应用于图像处理领域。它基于图像亮度的变化率来检测边缘的位置,主要通过计算图像中像素点的梯度来实现。 Sobel算子分为水平和垂直两个方向的算子,记作Gx和Gy。它们分别对图像进行水平和垂直方向的…...

ScrapeKit 和 Swift 编写程序
以下是一个使用 ScrapeKit 和 Swift 编写的爬虫程序,用于爬取 图片。同时,我们使用了proxy 这段代码来获取代理。 import ScrapeKit class PeopleImageCrawler: NSObject, ScrapeKit.Crawler {let url: URLlet proxyUrl: URL init(url: URL, proxy…...
)
Java基础面试题知识点总结(上篇)
大家好,我是栗筝i,从 2022 年 10 月份开始,我持续梳理出了全面的 Java 技术栈内容,一方面是对自己学习内容进行整合梳理,另一方面是希望对大家有所帮助,使我们一同进步。得到了很多读者的正面反馈。 而在 2…...
STM32进行LVGL裸机移植
本文的移植参考的是正点原子的课程《手把手教你学LVGL图形界面编程》 基于该课程和《LVGL开发指南_V1.3》“第二章 LVGL 无操作系统移植”,然后结合自身的实际情况进行整理。 先根据自己的习惯,创建基础的单片机工程,然后在APP业务层和DRIVE…...

python解析robot framework的output.xml并生成html
一、用pyh模块解析stat结点数据(output.py) #codingutf-8import xml.dom.minidom import xml.etree.ElementTree#打开xml文档 dom xml.dom.minidom.parse(./ui/output.xml);root2 xml.etree.ElementTree.parse(./ui/output.xml) #得到文档元素对象 ro…...

【RuoYi移动端】uni-app中的单击和双击事件
1、单击事件: click"enterpriseSelect" 2、双击事件: touchend"userinfo"...

使用 conda 在 Ubuntu 16.04 上安装 Python 3.9 的步骤:和 VSCode配置
一、使用conda在 Ubuntu 16.04 上安装 Python 3.9 的步骤: 当然可以,conda 是一个非常强大的包管理器,它可以方便地管理不同版本的 Python 和各种库包。以下是使用 conda 在 Ubuntu 16.04 上安装 Python 3.9 的步骤: 1. 安装 Miniconda Miniconda 是 Anaconda 的轻量级版…...
spring6-国际化:i18n | 数据校验:Validation
文章目录 1、国际化:i18n1.1、i18n概述1.2、Java国际化1.3、Spring6国际化1.3.1、MessageSource接口1.3.2、使用Spring6国际化 2、数据校验:Validation2.1、Spring Validation概述2.2、实验一:通过Validator接口实现2.3、实验二:B…...
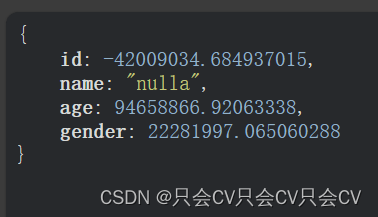
【MicroSoft Edge】格式化的显示JSON格式的数据
当我们没有进行任何操作的时候,默认浏览器给我们展示的JSON的数据是这样的: 看着十分不便。 解决方案: 首先点击 MicroSoft Edge 浏览器右上角的三点,如何选择扩展 点击 获取Microsoft Edge 扩展 搜索 JSONView,第一…...

【c++】跟webrtc学std array 2:TaskExecutorMap单例用法
D:\XTRANS\m98_rtc\ndrtc-webrtc\src\base\task\task_executor.ccstd array实现的map:TaskExecutorMap // Maps TaskTraits extension IDs to registered TaskExecutors. Index |n| // corresponds to id |n - 1|. using TaskExecutorMap =std::array<TaskExecutor*, Task…...

力扣每日一题59:螺旋矩阵||
题目描述: 给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。 示例 1: 输入:n 3 输出:[[1,2,3],[8,9,4],[7,6,5]]示例 2: 输入&am…...
codeforces (C++ In Love )
题目: 翻译: 思路: 1、在一个集合中有多组线段,如果有不相交的两组线段,则输出YES,否则输出NO。 2、每次操纵可以选择增加一组线段或者删除一组线段后,输出YES或者NO。 3、用flag标记该线段是否…...

【python】py文件全自动打包成spec文件
说明: 自动获取当前根目录下所有py文件生成spec文件,直接运行pyinstaller进行打包即可。直接打包成单执行文件。 直接上代码 import ospathex []def recursion(path, main):if path[:1] ! /:path /listpath os.listdir(path)for item in listpath:if…...
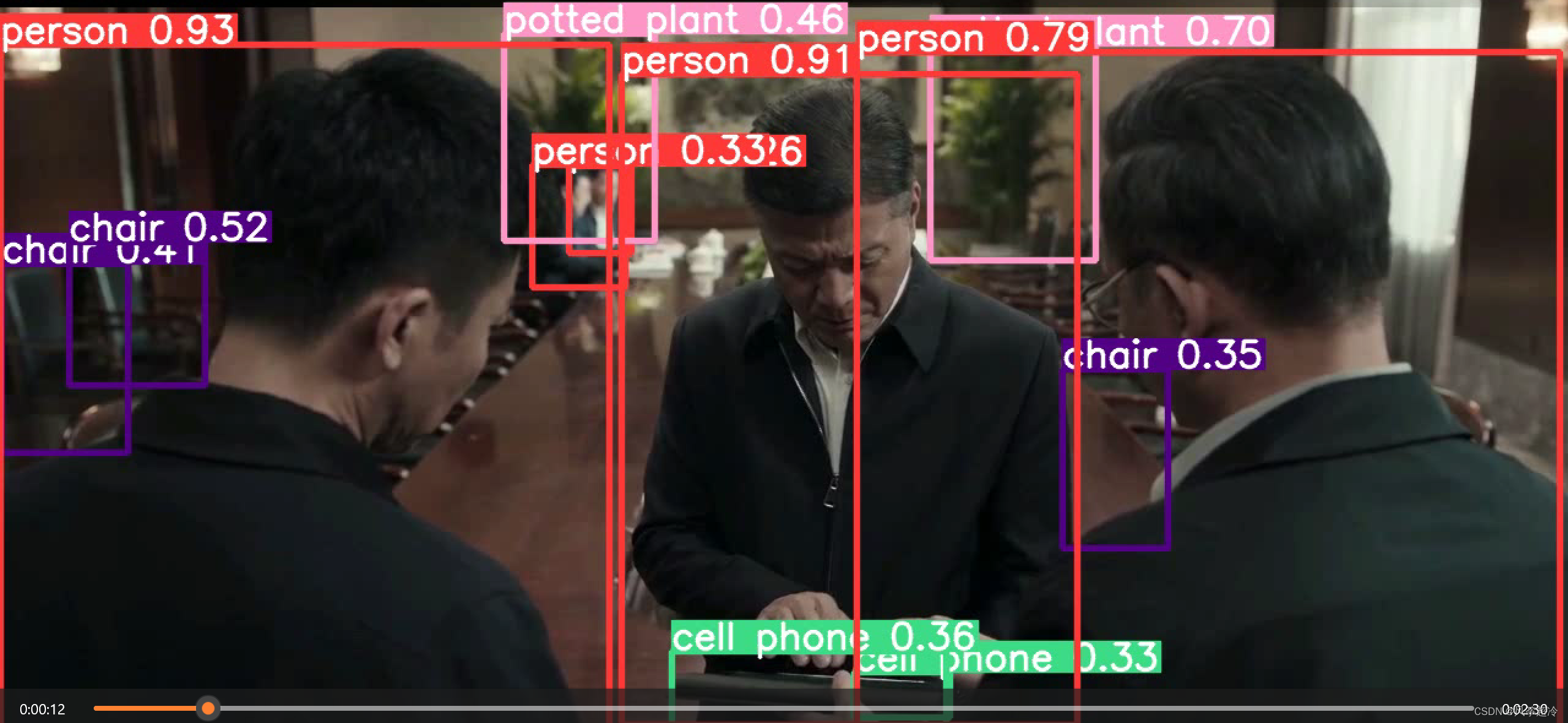
YOLOv5-调用官方权重进行检验(目标检测)
🍨 本文为[🔗365天深度学习训练营学习记录博客 🍦 参考文章:365天深度学习训练营-第7周:咖啡豆识别(训练营内部成员可读) 🍖 原作者:[K同学啊 | 接辅导、项目定制](https…...

springMVC中统一异常处理@ControllerAdvice
1.在DispatcherServlet中初始化HandlerExceptionResolver 2.controller执行完成后执行processDispatchResult(processedRequest,response,mappedHandler,mv,dispatchException),有异常则处理异常 3.ExcepitonHandlerExceptionResolver中执行方法doResolveHandlerMethodExceptio…...

【Java】<泛型>,在编译阶段约束操作的数据结构,并进行检查。
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ JAVA泛型 泛型介绍: ①泛型&#…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
生成对抗网络(GAN)损失函数解读
GAN损失函数的形式: 以下是对每个部分的解读: 1. , :这个部分表示生成器(Generator)G的目标是最小化损失函数。 :判别器(Discriminator)D的目标是最大化损失函数。 GAN的训…...
