每日一题——L1-085 试试手气(15)
L1-085 试试手气

我们知道一个骰子有 6 个面,分别刻了 1 到 6 个点。下面给你 6 个骰子的初始状态,即它们朝上一面的点数,让你一把抓起摇出另一套结果。假设你摇骰子的手段特别精妙,每次摇出的结果都满足以下两个条件:
- 每个骰子摇出的点数都跟它之前任何一次出现的点数不同;
- 在满足条件 1 的前提下,每次都能让每个骰子得到可能得到的最大点数。
那么你应该可以预知自己第 n 次(1≤n≤5)摇出的结果。
输入格式:
输入第一行给出 6 个骰子的初始点数,即 [1,6] 之间的整数,数字间以空格分隔;第二行给出摇的次数 n(1≤n≤5)。
输出格式:
在一行中顺序列出第 n 次摇出的每个骰子的点数。数字间必须以 1 个空格分隔,行首位不得有多余空格。
输入样例:
3 6 5 4 1 4
3
输出样例:
4 3 3 3 4 3
样例解释:
这 3 次摇出的结果依次为:
6 5 6 6 6 6
5 4 4 5 5 5
4 3 3 3 4 3
分析
其实这道题除了一步步算之外,还可以运用数学方法来寻找规律。根据题目条件,我们知道它其实每个骰子每次的点数都是可以取的最大值,其实n次后的值就是[6,5,4,3,2,1]中去除本身后的第n个数。而这可以转化为7-n,但是需要注意:当dice[i]+n>6时,最终的点数比本身小,所以需要跳过自身的数,也就是6-n的表达式(其实完整表达式写出来就是:dice[i]-(n-(6-dice[i])),减去还要往下数多少个数)。
P.S.注意输出不能有多余空格
代码
#include<bits/stdc++.h>
using namespace std;
int main(){int dice[6];int i,n;for(i=0;i<6;i++){cin>>dice[i];}cin>>n;for(i=0;i<6;i++){if(i)cout<<" ";if(dice[i]+n>6){//cout<<dice[i]-(n-(6-dice[i]));cout<<6-n;}else{cout<<7-n;}}return 0;
}
相关文章:

每日一题——L1-085 试试手气(15)
L1-085 试试手气 我们知道一个骰子有 6 个面,分别刻了 1 到 6 个点。下面给你 6 个骰子的初始状态,即它们朝上一面的点数,让你一把抓起摇出另一套结果。假设你摇骰子的手段特别精妙,每次摇出的结果都满足以下两个条件:…...
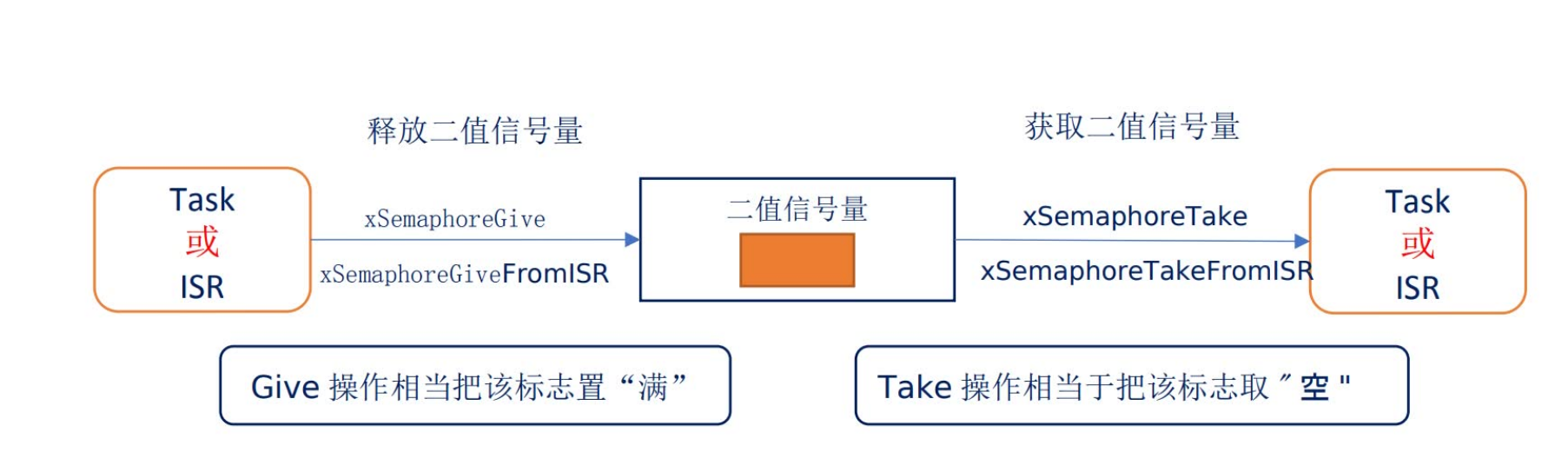
FreeRTOS信号量
前面介绍过,队列(queue)可以用于传输数据:在任务之间,任务和中断之间。消息队列用于传输多个数据,但是有时候我们只需要传递一个状态,这个状态值需要用一个数值表示,比如:…...
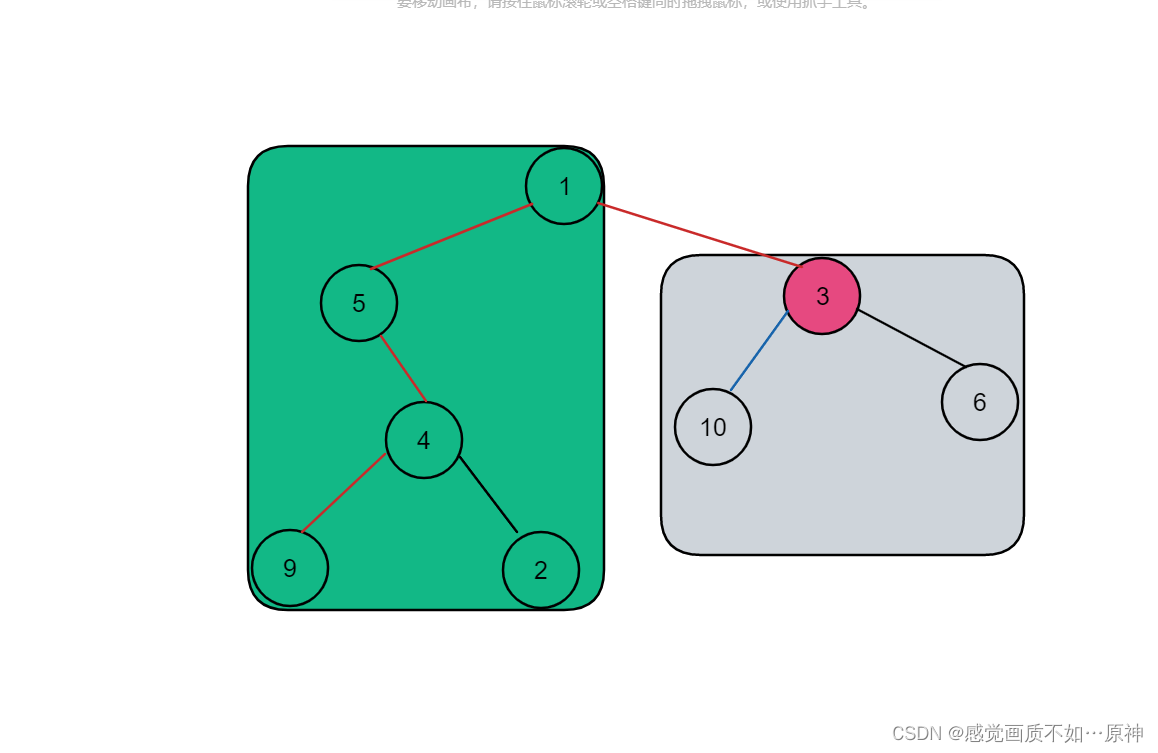
Leetcode.2385 感染二叉树需要的总时间
题目链接 Leetcode.2385 感染二叉树需要的总时间 Rating : 1711 题目描述 给你一棵二叉树的根节点 root,二叉树中节点的值 互不相同 。另给你一个整数 start。在第 0分钟,感染 将会从值为 start的节点开始爆发。 每分钟,如果节点…...

[蓝桥杯 2022 国 B] 卡牌(贪心/二分)
题目传送门 该题第一思路是想去模拟题目中所描述的过程 这里我选择从大到小遍历可能凑出的牌套数,计算凑出它需要补的牌数以及判断是否会超出能补的牌数 #include<iostream> #include<climits> #include<vector> #include<algorithm> #def…...
1301:大盗阿福
经典的dp打家劫舍问题状态设计dp[i][0]:在前i个店铺中选,且不选第i家的最大和dp[i][1]:在前i个店铺中选,且选第i家的最大和状态转移dp[i][0] max(dp[i-1][1], dp[i-1][0];第i家店不选,那么我们可以选第i-1个店 也可以…...
Netty——序列化的作用及自定义协议
序列化的作用及自定义协议序列化的重要性大小对比效率对比自定义协议序列化数据结构自定义编码器自定义解码器安全性验证NettyClientNettyServerNettyClientTestHandlerNettyServerTestHandler结果上一章已经说了怎么解决沾包和拆包的问题,但是这样离一个成熟的通信…...
)
一起Talk Android吧(第五百零五回:如何调整组件在约束布局中的大小)
文章目录 背景介绍调整方法各位看官们大家好,上一回中咱们说的例子是"如何调整组件在约束布局中的位置",这一回中咱们说的例子是" 如何调整组件在约束布局中的大小"。闲话休提,言归正转, 让我们一起Talk Android吧! 背景介绍 在使用约束(constraintl…...

【数据库】数据库的完整性
第五章 数据库完整性 数据库完整性 数据库的完整性是指数据的正确性和相容性 数据的正确性是指数据是符合现实世界语义,反映当前实际状况的数据的相容性是指数据库的同一对象在不同的关系中的数据是符合逻辑的 关系模型中有三类完整性约束:实体完整性…...

基因净化车间装修设计方案SICOLAB
基因净化车间的设计方案应该根据实际需求进行定制,以下是一些规划建设要点和洁净设计要注意的事项:一、净化车间规划建设要点:(1)基因车间的面积应该根据实验项目的规模进行规划,包括充足的操作区域和足够的…...
java 内部类的四种“写法”
基本介绍语法格式分类成员内部类静态内部类局部内部类匿名内部类(🐂🖊)一、基本介绍 : 1.概述当一个类的内部又完整地嵌套了另一个类时,被嵌套于内部的“内核”我们称之为“内部类”(inner class);而包含该…...

【python】main方法教程
嗨害大家好鸭! 我是小熊猫~ 首先 if name "main": 可以看成是python程序的入口, 就像java中的main()方法, 但不完全正确。 事实上python程序是从上而下逐行运行的, 在.py文件中, 除…...

公司对不同职级能力抽象要求的具体化
要先把当前级别要求的能力提升到精通,然后尝试做下一级别的事情。 但可能不确定高一级的能力要求究竟怎样,不同Title,如“工程师”“高级工程师”和“资深工程师”等。但这样 Title 对我们理解不同级别的能力要求,完全无用。“高…...

Java之MinIO存储桶和对象API使用
环境搭建 创建一个 maven项目,引入依赖: <!-- minio依赖--><dependency><groupId>io.minio</groupId><artifactId>minio</artifactId><version>8.3.3</version></dependency><!-- 官方 minio…...

如何用java实现同时进行多个请求,可以将它们并行执行,从而减少总共的请求时间。
1.使用线程池 通过使用Java提供的线程池,可以将多个请求分配到不同的线程中并行执行。可以通过创建固定数量的线程池,然后将请求分配给线程池来实现。线程池会自动管理线程的数量和复用,从而减少了线程创建和销毁的开销,提高了程序…...
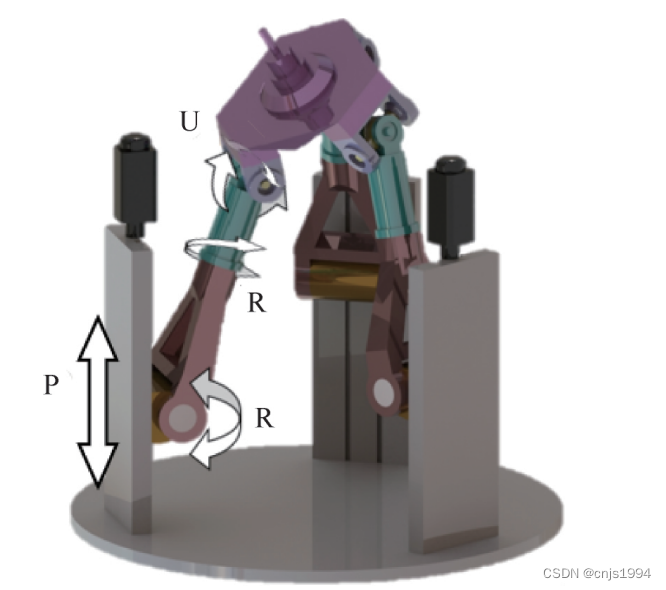
高端装备的AC主轴头结构
加工机器人的AC主轴头和位置相关动力学特性1. 位置依赖动态特性及其复杂性2. AC主轴头2.1 常见主轴头摆角结构2.2 摆动机构3. 加装AC主轴头的作用和局限性4. 切削机器人的减速器类型5. 其他并联结构形式参考文献资料1. 位置依赖动态特性及其复杂性 However, FRF measurements …...
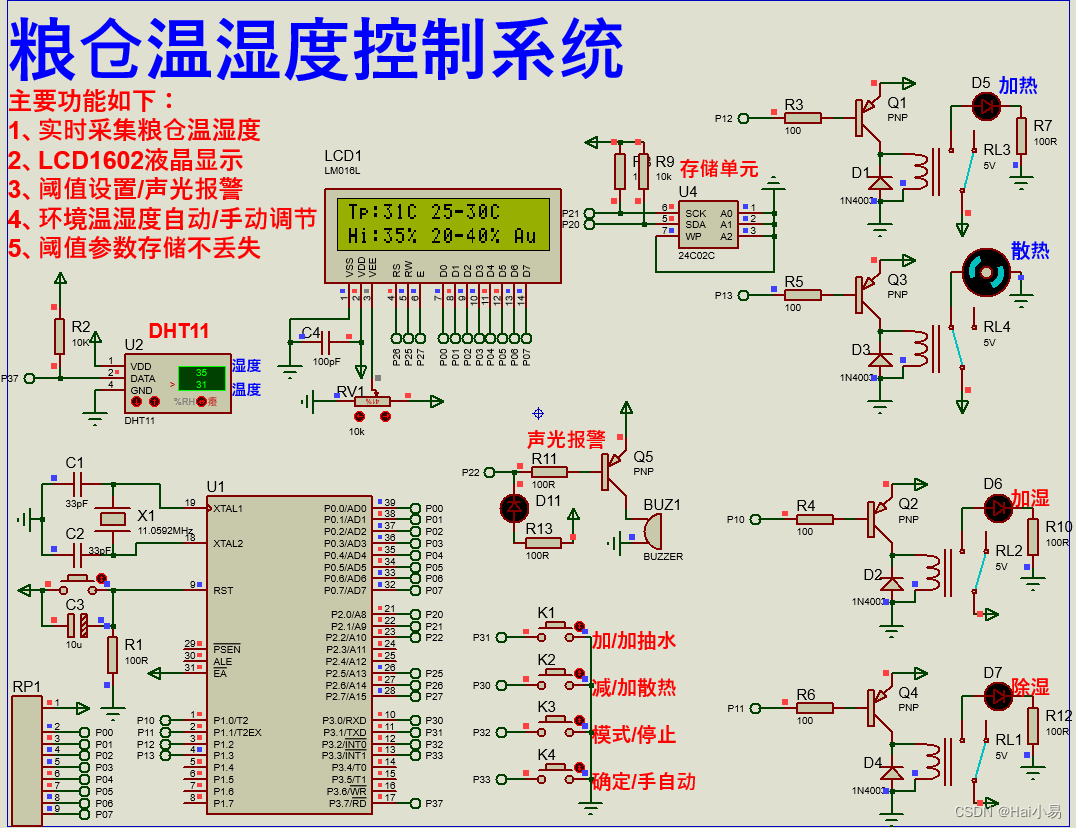
【Proteus仿真】【51单片机】粮仓温湿度控制系统设计
文章目录一、功能简介二、软件设计三、实验现象联系作者一、功能简介 本项目使用Proteus8仿真51单片机控制器,使用声光报警模块、LCD1602显示模块、DHT11温湿度模块、继电器模块、加热加湿除湿风扇等。 主要功能: 系统运行后,LCD1602显示传…...
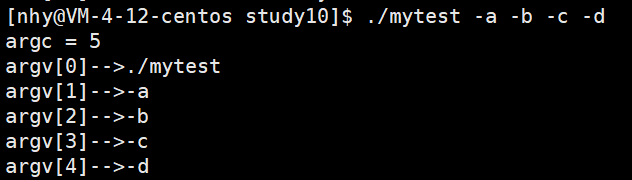
【LINUX】环境变量以及main函数的参数
文章目录前言环境变量常见环境变量:设置环境变量:和环境变量相关的命令:环境变量的组织方式:获取环境变量环境变量可以被子进程继承环境变量总结main函数的参数前言 大家好久不见,今天分享的内容是环境变量和main函数…...

使用Pyparsing为嵌入式开发定义自己的脚本语言
Python在嵌入式开发中也很流行生成实用脚本。Pyparsing还允许你轻松地定义在Python上下文中运行的定制脚本语言。Python实现的系统旨在能够独立执行用户传递的一系列命令。你希望系统以脚本的形式接收命令。用户应该能够定义条件。这种对通信中逻辑元素的最初简单的声音要求&am…...
)
C win32基础学习(二)
上一篇我们已经介绍了关于窗口程序的一些基本知识。从本篇开始我们将正式进入C win32的学习中去。 正文 窗口创建过程 定义WinMain函数 定义窗口处理函数(自定义,处理消息) 注册窗口类(向操作系统写入一些数据) 创建窗口(内存…...

理论五:控制反转、依赖反转、依赖注入,这三者有何区别和联系?
关于SOLID原则,我们已经学过单一职责、开闭、里式替换、接口隔离这四个原则。今天,我们再来学习最后一个原则:依赖反转原则。在前面几节课中,我们讲到,单一职责原则和开闭原则的原理比较简单,但是,想要在实践中用好却比较难。而今天我们要讲到的依赖反转原则正好相反。这个原则…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
