jianzhiOffer第二版难重点记录
04. 二维数组中的查找 https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/
https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/
思路:可以每层用以恶搞二分查找,优化思路:从左下角出发直接用二分。
07. 重建二叉树![]() https://leetcode.cn/problems/zhong-jian-er-cha-shu-lcof/
https://leetcode.cn/problems/zhong-jian-er-cha-shu-lcof/
思路:根据前序遍历和中序遍历来确定最终的树。
19. 正则表达式匹配![]() https://leetcode.cn/problems/zheng-ze-biao-da-shi-pi-pei-lcof/
https://leetcode.cn/problems/zheng-ze-biao-da-shi-pi-pei-lcof/
递归或者是动态规划
func isMatch(s string, p string) bool {dp := make([][]bool , len(s) + 1)for i := 0 ; i <= len(s); i++{dp[i] = make([]bool , len(p) + 1)}dp[0][0] = truefor i := 1 ; i <= len(p); i++{ // s的长度为0的时候初始化if (i % 2) == 0 && p[i-1] == '*'{dp[0][i] = dp[0][i-2] }}for i := 1; i <= len(s); i++{for j := 1 ; j <= len(p); j++{// 当前值相等的时候if p[j - 1] == '.' || p[j-1] == s[i - 1]{dp[i][j] = dp[i-1][j-1]}// 若果为*的时候考虑if p[j-1] == '*'{dp[i][j] = dp[i][j-2] // 表示当前x*为空if p[j-2] == '.' || p[j-2] == s[i-1]{ // 如果x等于当前值的话可以取一个x*,这里表示s[i-1]已经被解决了dp[i][j] = dp[i][j] || dp[i-1][j]}}} }return dp[len(s)][len(p)]
}递归的写法
func isMatch(s string, p string) bool {if len(p) == 0 && len(s) == 0{return true}if len(p) == 0{return false}if len(s) == 0{if len(p) >= 2 && p[1] == '*'{return isMatch(s , p[2:])}return false}if len(p) >= 2 && p[1] == '*'{if p[0] == '.' || s[0] == p[0]{return isMatch(s,p[2:]) || isMatch(s[1:] , p)}else{return isMatch(s , p[2:])}}else {if p[0] == '.' || s[0] == p[0]{return isMatch(s[1:] , p[1:])}}return false
}30. 包含min函数的栈![]() https://leetcode.cn/problems/bao-han-minhan-shu-de-zhan-lcof/
https://leetcode.cn/problems/bao-han-minhan-shu-de-zhan-lcof/
如何实现一个包含最小值的栈,要能O(1)的时间获取最小值,有两种思路,第一种可以考虑用一个链表去模拟栈,维护一个最小值的变量,第二种方案可以考虑用一个辅助栈去存储最小的值。
type MinStack struct {a []intb []int
}/** initialize your data structure here. */
func Constructor() MinStack {return MinStack{[]int{}, []int{math.MaxInt32},}
}
func min(i, j int) int {if i < j {return i}return j
}
func (this *MinStack) Push(x int) {this.a = append(this.a, x)this.b = append(this.b, min(x, this.b[len(this.b)-1]))
}func (this *MinStack) Pop() {this.a = this.a[:len(this.a)-1]this.b = this.b[:len(this.b)-1]
}func (this *MinStack) Top() int {return this.a[len(this.a)-1]
}func (this *MinStack) Min() int {return this.b[len(this.b)-1]
}33.二叉搜索树的后序遍历序列![]() https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/
https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/
根据后续遍历:左右根,根的左右小于,根的右边大于
func verifyPostorder(postorder []int) bool {// 思路 找到右节点// 右节点的右边大于右节点的左边var recursion func(left , right int)boolrecursion = func(left , right int)bool{if left >= right {return true}index := left for index <= right && postorder[index] < postorder[right]{index++}index --for i := index + 1 ; i < right ; i++{if postorder[i] < postorder[right]{return false}}return recursion(left , index) && recursion(index + 1 , right - 1)}return recursion(0 , len(postorder)-1)
}43. 1~n 整数中 1 出现的次数![]() https://leetcode.cn/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof/
https://leetcode.cn/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof/
每个位置进行统计。
func countDigitOne(n int) int {// 统计每个位置出现的1的次数s := strconv.Itoa(n)clen := len(s)res := 0for i := clen - 1; i >= 0; i-- {base := int(math.Pow(10, float64(clen-i-1))) // 表示当前位置的倍数left := 0 //当前位置左边的数right := 0 // 当前位置右边的数for j := 0; j < i; j++ {left = left*10 + int(s[j]-'0')}for j := i + 1; j < clen; j++ {right = right*10 + int(s[j]-'0')}left++ //包括左边的全0,left++right ++ // 右边包括0,right++switch s[i] {case '0': // 左右有left种可能,为1*base - 19..,有left*base可能i位置为1,因为该位置为0,因此left减少一位。res = res + (left - 1)*basecase '1':res = res + (left - 1)*base + right // left减少一位,补上右边的可能性default:res = res + left*base }}return res
}44. 数字序列中某一位的数字![]() https://leetcode.cn/problems/shu-zi-xu-lie-zhong-mou-yi-wei-de-shu-zi-lcof/
https://leetcode.cn/problems/shu-zi-xu-lie-zhong-mou-yi-wei-de-shu-zi-lcof/
func findNthDigit(n int) int {if n == 0 {return 0}start := 1count := 9length := 1for n > count {n -= countstart *= 10length++count = 9 * start * length}index := (n - 1) / length + startyu := (n - 1) % lengthreturn int(strconv.Itoa((index))[yu] - '0')
}
/* 数字范围 数量 位数 占多少位1-9 9 1 910-99 90 2 180100-999 900 3 27001000-9999 9000 4 36000 ...例如 2901 = 9 + 180 + 2700 + 12 即一定是4位数,第12位 n = 12;数据为 = 1000 + (12 - 1)/ 4 = 1000 + 2 = 1002定位1002中的位置 = (n - 1) % 4 = 3 s.charAt(3) = 2;*/49. 丑数![]() https://leetcode.cn/problems/chou-shu-lcof/
https://leetcode.cn/problems/chou-shu-lcof/
堆的应用
51. 数组中的逆序对![]() https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/
https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/
归并方法思路
func reversePairs(nums []int) int {res := 0tep := make([]int, len(nums))var mergeSort func(left, right int)merge := func(left, mid, right int) {i := leftj := mid + 1index := leftfor i <= mid && j <= right {if nums[i] > nums[j] {tep[index] = nums[j]// fmt.Println("1111")res = res + (mid - i + 1)j++} else {tep[index] = nums[i]i++}index++}for i <= mid {tep[index] = nums[i]i++index++}for j <= right {tep[index] = nums[j]j++index++}for i := left; i <= right; i++ {nums[i] = tep[i]}}mergeSort = func(left, right int) {if left >= right {return}mid := left + (right-left)/2mergeSort(left, mid)mergeSort(mid+1, right)merge(left, mid, right)}mergeSort(0, len(nums)-1)return res
}
56 - I. 数组中数字出现的次数![]() https://leetcode.cn/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-lcof/
https://leetcode.cn/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-lcof/
数组中所有数字都出现两次,有两个出现一次的数字,找出来,这个就是利用二进制的原理进行分组,先全部异或,取出两数已获结果,在通过(n&-n)取出第一位置不一样的作为分组标志。
60n个骰子的点数![]() https://leetcode.cn/problems/nge-tou-zi-de-dian-shu-lcof/
https://leetcode.cn/problems/nge-tou-zi-de-dian-shu-lcof/
//浪费空间的写法,但是比较容易理解
func dicesProbability(n int) []float64 {dp := make([][]float64, n+1) // dp[i][j] 表示i个骰子,点数和为j的概率for i := 1; i <= n; i++ {dp[i] = make([]float64, 6*i+1)}for i := 1; i <= 6; i++ {dp[1][i] = float64(1) / 6}for i := 2; i <= n; i++ {for k := i; k <= 6*i; k++ { // 当前的点数for t := 1; t <= 6 && k > t; t++ { // 当前出现的点数if k-t <= 6*(i-1) { // 上一级合法出现的点数dp[i][k] += dp[i-1][k-t] / 6 // 上一级出现的点数}}}}return dp[n][n:]
}func dicesProbability(n int) []float64 {dp := make([]float64, 6)for i := 0; i < 6; i++ {dp[i] = float64(1) / 6}for i := 1; i < n; i++ {tep := make([]float64, 6*(i+1)-i)for j := 0; j < len(dp); j++ {for t := 0; t < 6; t++ {tep[j+t] = tep[j+t] + dp[j]/6}}dp = tep}return dp
}62. 圆圈中最后剩下的数字![]() https://leetcode.cn/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/
https://leetcode.cn/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/
思路:有三种解法,第一通过数组,第二通过链表,第三,递归去做,定义一个递归函数,f(n , k , i)表示有n个数,当删除第k个数,i表示正在删除第i次。
func lastRemaining(n int, m int) int {var f func(n , m , i int)intf = func (n , m , i int)int{if i == 1{return (n + m - 1) % n}return (f(n - 1 , m , i - 1) + m ) % n}return f(n , m , n)
}
64. 求1+2+…+n![]() https://leetcode.cn/problems/qiu-12n-lcof/
https://leetcode.cn/problems/qiu-12n-lcof/
思路:不能使用公式、乘除法,for等,等价for得有递归操作。还可以用快速乘来替代普通的乘法。
65. 不用加减乘除做加法![]() https://leetcode.cn/problems/bu-yong-jia-jian-cheng-chu-zuo-jia-fa-lcof/
https://leetcode.cn/problems/bu-yong-jia-jian-cheng-chu-zuo-jia-fa-lcof/
思路:传统思路会直接按位进行计算,优化思路的话,可以考虑用递归的思路,a于b之和可以分为无进位之和和有进位之和,无进位是a^b,有进位的和是(a&b)<<1,对结果进行递归处理,当进位为0的时候,直接返回无进位和就行。
func add(a int, b int) int {if b == 0 {return a}return add(a ^ b , (a & b ) << 1)
}相关文章:
jianzhiOffer第二版难重点记录
04. 二维数组中的查找https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/ 思路:可以每层用以恶搞二分查找,优化思路:从左下角出发直接用二分。 07. 重建二叉树https://leetcode.cn/problems/zhong-jian-er-cha…...

C语言 | 问题20230225
C语言 | 问题20230225 文章目录C语言 | 问题202302251.问题1无限循环2.问题2C 中的运算符优先级实例1:1.问题1 Which slice of the following code is NOT endless loop? 以下代码的哪一部分不是无限循环? A for (;(cgetchar())!\n; ) printf("*c&…...
【机器学习笔记】Python基础笔记
目录基础语法加载数据:pd.read_csv查看数据大小:shape浏览数据行字段:columns浏览少量数据:head()浏览数据概要:describe()基础功能语法缺省值去除缺失值:dropna按行删除:存在空值,即…...

js-DOM03-DOM对CSS的操作
DOM对CSS的操作 - 读取和修改内联样式 - 使用style属性来操作元素的内联样式 - 读取内联样式: 语法:元素.style.样式名 - 例子: 元素.style.width 元素.style.…...

tun驱动之tun_init
tun驱动的初始化方法是tun_init。 static int __init tun_init(void) {int ret 0;pr_info("%s, %s\n", DRV_DESCRIPTION, DRV_VERSION);ret rtnl_link_register(&tun_link_ops);if (ret) {pr_err("Cant register link_ops\n");goto err_linkops;}re…...

模拟退火算法优化bp
%% 基于模拟退火遗传算法优化BP神经网络的钢带厚度预测 clear clc close all format short %% 加载训练数据 Xtrxlsread(train_data.xlsx); DDsize(Xtr,2); input_trainXtr(:,1:DD-1);% output_trainXtr(:,DD);% %% 加载测试数据 Xtexlsread(test_data.xlsx); input_testXte(…...
【NFC音乐相册】简易制作
欢迎来到 Claffic 的博客 💞💞💞 前言: NFC音乐相册在前段时间火了一把,想必大家都听过了,最近我刷到了这个东西,闲来无事就弄了几个,这篇博客就记录下制作工序。 注:我所…...

每日一题——L1-085 试试手气(15)
L1-085 试试手气 我们知道一个骰子有 6 个面,分别刻了 1 到 6 个点。下面给你 6 个骰子的初始状态,即它们朝上一面的点数,让你一把抓起摇出另一套结果。假设你摇骰子的手段特别精妙,每次摇出的结果都满足以下两个条件:…...
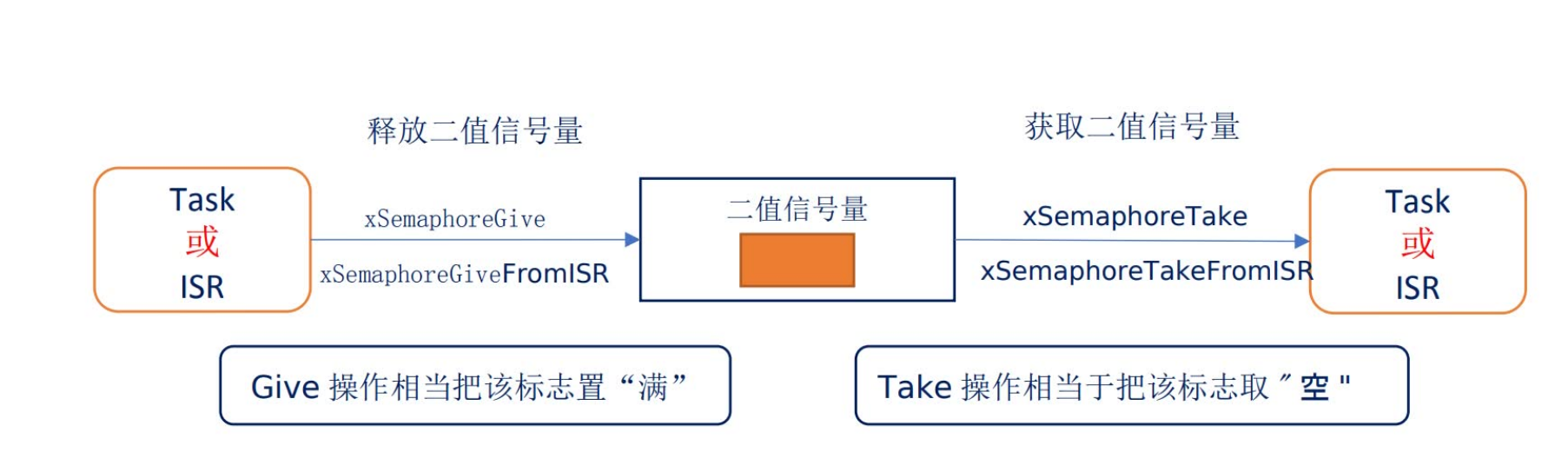
FreeRTOS信号量
前面介绍过,队列(queue)可以用于传输数据:在任务之间,任务和中断之间。消息队列用于传输多个数据,但是有时候我们只需要传递一个状态,这个状态值需要用一个数值表示,比如:…...
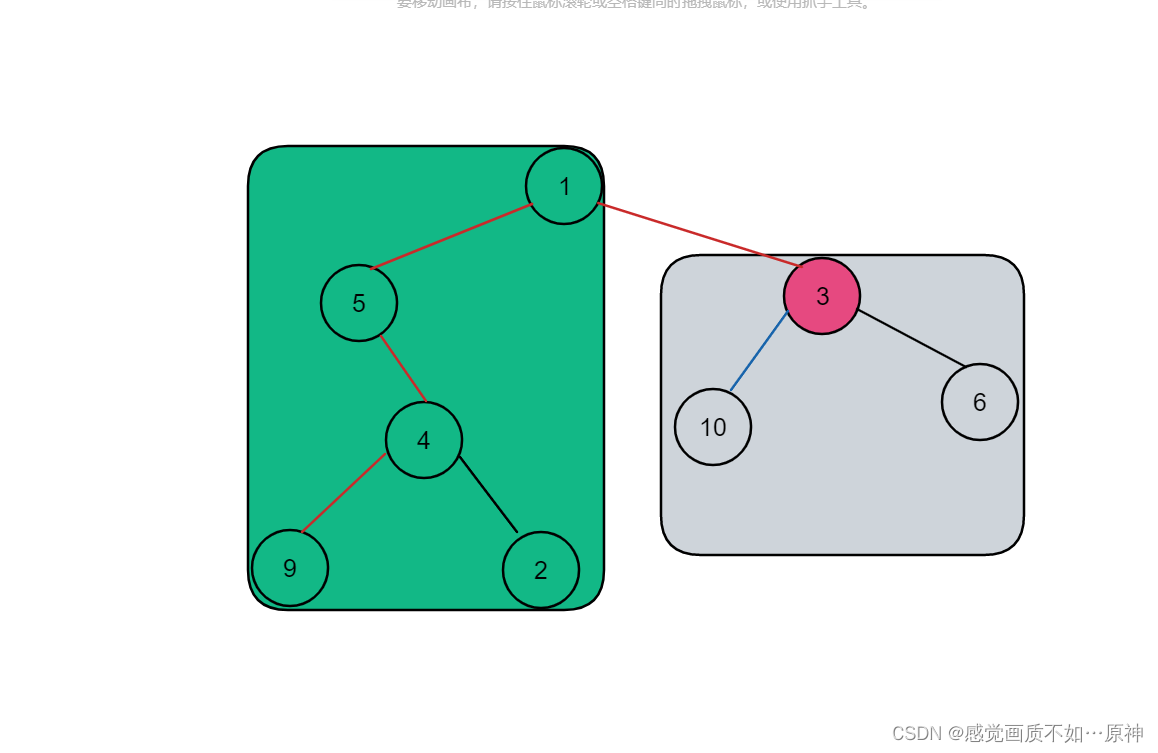
Leetcode.2385 感染二叉树需要的总时间
题目链接 Leetcode.2385 感染二叉树需要的总时间 Rating : 1711 题目描述 给你一棵二叉树的根节点 root,二叉树中节点的值 互不相同 。另给你一个整数 start。在第 0分钟,感染 将会从值为 start的节点开始爆发。 每分钟,如果节点…...

[蓝桥杯 2022 国 B] 卡牌(贪心/二分)
题目传送门 该题第一思路是想去模拟题目中所描述的过程 这里我选择从大到小遍历可能凑出的牌套数,计算凑出它需要补的牌数以及判断是否会超出能补的牌数 #include<iostream> #include<climits> #include<vector> #include<algorithm> #def…...
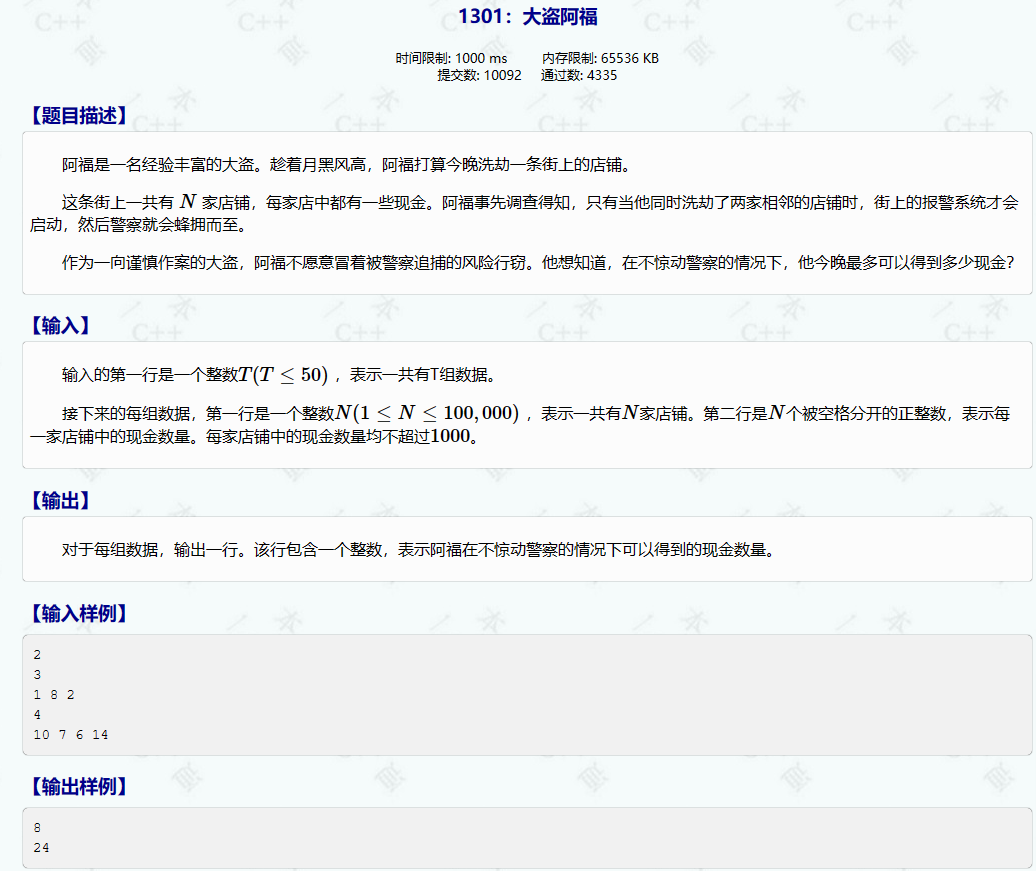
1301:大盗阿福
经典的dp打家劫舍问题状态设计dp[i][0]:在前i个店铺中选,且不选第i家的最大和dp[i][1]:在前i个店铺中选,且选第i家的最大和状态转移dp[i][0] max(dp[i-1][1], dp[i-1][0];第i家店不选,那么我们可以选第i-1个店 也可以…...
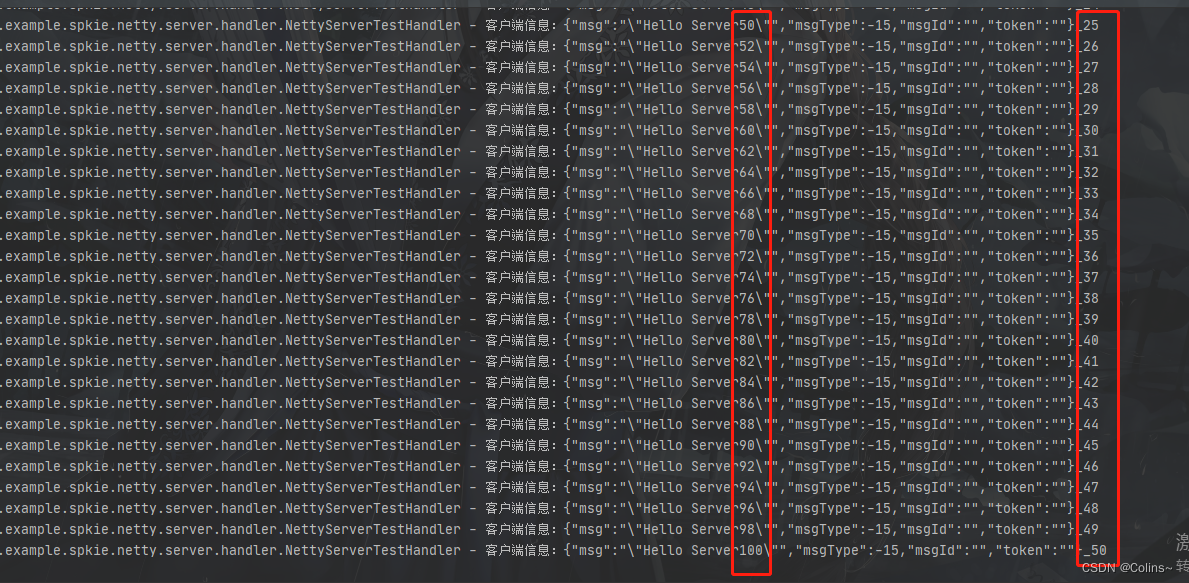
Netty——序列化的作用及自定义协议
序列化的作用及自定义协议序列化的重要性大小对比效率对比自定义协议序列化数据结构自定义编码器自定义解码器安全性验证NettyClientNettyServerNettyClientTestHandlerNettyServerTestHandler结果上一章已经说了怎么解决沾包和拆包的问题,但是这样离一个成熟的通信…...
)
一起Talk Android吧(第五百零五回:如何调整组件在约束布局中的大小)
文章目录 背景介绍调整方法各位看官们大家好,上一回中咱们说的例子是"如何调整组件在约束布局中的位置",这一回中咱们说的例子是" 如何调整组件在约束布局中的大小"。闲话休提,言归正转, 让我们一起Talk Android吧! 背景介绍 在使用约束(constraintl…...

【数据库】数据库的完整性
第五章 数据库完整性 数据库完整性 数据库的完整性是指数据的正确性和相容性 数据的正确性是指数据是符合现实世界语义,反映当前实际状况的数据的相容性是指数据库的同一对象在不同的关系中的数据是符合逻辑的 关系模型中有三类完整性约束:实体完整性…...

基因净化车间装修设计方案SICOLAB
基因净化车间的设计方案应该根据实际需求进行定制,以下是一些规划建设要点和洁净设计要注意的事项:一、净化车间规划建设要点:(1)基因车间的面积应该根据实验项目的规模进行规划,包括充足的操作区域和足够的…...
java 内部类的四种“写法”
基本介绍语法格式分类成员内部类静态内部类局部内部类匿名内部类(🐂🖊)一、基本介绍 : 1.概述当一个类的内部又完整地嵌套了另一个类时,被嵌套于内部的“内核”我们称之为“内部类”(inner class);而包含该…...

【python】main方法教程
嗨害大家好鸭! 我是小熊猫~ 首先 if name "main": 可以看成是python程序的入口, 就像java中的main()方法, 但不完全正确。 事实上python程序是从上而下逐行运行的, 在.py文件中, 除…...

公司对不同职级能力抽象要求的具体化
要先把当前级别要求的能力提升到精通,然后尝试做下一级别的事情。 但可能不确定高一级的能力要求究竟怎样,不同Title,如“工程师”“高级工程师”和“资深工程师”等。但这样 Title 对我们理解不同级别的能力要求,完全无用。“高…...

Java之MinIO存储桶和对象API使用
环境搭建 创建一个 maven项目,引入依赖: <!-- minio依赖--><dependency><groupId>io.minio</groupId><artifactId>minio</artifactId><version>8.3.3</version></dependency><!-- 官方 minio…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
