施密特正交化
相信大家在平时的期末考试中一定少不了对某某向量组执行标准正交化类型的题目。今天我们从这个题目入手,说明这个如何执行施密特正交化,以及为什么要进行正交化。


一、例子
例子:设 a 1 = [ 1 2 − 1 ] a_1=\begin{bmatrix}1\\2\\-1\end{bmatrix} a1= 12−1 , a 2 = [ − 1 3 1 ] a_2=\begin{bmatrix}-1\\3\\1\end{bmatrix} a2= −131 , a 3 = [ 4 − 1 0 ] a_3=\begin{bmatrix}4\\-1\\0\end{bmatrix} a3= 4−10 使用施密特正交化将这组向量标准正交化。
答:标准正交向量组应该满足:
- 向量的长度为1;
- 向量之间相互正交;
选定一个基准向量
A 1 = a 1 = [ 1 2 − 1 ] A_1=a_1=\begin{bmatrix}1\\2\\-1\end{bmatrix} A1=a1= 12−1
对第二个向量分解为正交和与 A 1 A_1 A1 共线的两个向量,其中与 A 1 A_1 A1 共线的向量因为已经能够用 A 1 A_1 A1 进行表示,所以应该剔除只保留与 A 1 A_1 A1 正交的分量:
A 2 = A 2 − P A 1 A 2 = A 2 − A 1 A 1 T A 1 T A 1 A 2 = 5 3 [ − 1 1 1 ] A_2=A_2-P_{A_1}A_2=A_2-\frac{A_1A_1^T}{A_1^TA_1}A_2=\frac{5}{3}\begin{bmatrix}-1\\1\\1\end{bmatrix} A2=A2−PA1A2=A2−A1TA1A1A1TA2=35 −111
同理:
A 3 = A 3 − A 2 A 2 T A 2 T A 2 A 3 − A 3 A 3 T A 3 T A 3 A 3 = 2 [ 1 0 1 ] A_3=A_3-\frac{A_2A_2^T}{A_2^TA_2}A_3-\frac{A_3A_3^T}{A_3^TA_3}A_3=2\begin{bmatrix}1\\0\\1\end{bmatrix} A3=A3−A2TA2A2A2TA3−A3TA3A3A3TA3=2 101
已经正交化的向量应该更新到下一个阶段的计算。
接下来对向量组的每个成员进行单位化。
单位化的长度可以随便缩小,总之保证模长度为1即可,也就是说前面的诸如 2 2 2 和 5 3 \frac{5}{3} 35 完全不用考虑其存在。
e 1 = A 1 ∣ A 1 ∣ = 1 6 [ 1 2 − 1 ] e 2 = A 2 ∣ A 2 ∣ = 1 3 [ − 1 1 1 ] e 3 = A 3 ∣ A 3 ∣ = 1 2 [ 1 0 1 ] e_1=\frac{A1}{|A1|}=\frac{1}{\sqrt 6}\begin{bmatrix}1\\2\\-1\end{bmatrix}\\ e_2=\frac{A2}{|A2|}=\frac{1}{\sqrt 3}\begin{bmatrix}-1\\1\\1\end{bmatrix}\\ e_3=\frac{A3}{|A3|}=\frac{1}{\sqrt 2}\begin{bmatrix}1\\0\\1\end{bmatrix} e1=∣A1∣A1=61 12−1 e2=∣A2∣A2=31 −111 e3=∣A3∣A3=21 101
如果你动手计算的话,你会发现得到正交化的结果并不容易。所以为什么我们要废这么大功夫去实现这样的一个分解?接下来就是对这个问题进行解答。
二、正交化的应用
谈到正交化, Q R QR QR 分解是经常一起谈论的。 Q R QR QR 分解是将一个矩阵分解为正交矩阵 Q Q Q 和上三角矩阵 R R R 的过程。很多方法可以实现这样的一个分解,上面的例子我们就使用到了施密特正交化的方法。下面是各种方法的比较:
| 方法 | 描述 | 优缺点 | 使用场景 |
|---|---|---|---|
| Gram-Schmidt过程 | 是一种迭代方法,逐列地将原始矩阵的列向量正交化 | 直观但是可能数值不稳定,尤其是当 A A A的列近似线性相关时 | 小到中型矩阵 |
| Householder变换 | 利用对称反射来逐步将矩阵变换为上三角形式的方法 | 通常比Gram-Schmidt过程更数值稳定。是许多数值线性代数库(如LAPACK)的标准方法 | 大型、满秩的密集矩阵 |
| Givens旋转 | 通过旋转来逐步零化矩阵元素,达到上三角形式 | 通常用于稀疏矩阵或特定结构的矩阵,因为可以有选择地零化矩阵的元素 | 大型、稀疏矩阵 |
| 列主元 Q R QR QR分解 | 在 Q R QR QR分解中引入列主元策略,每一步中选择“最大”的列作为下一个正交向量 | 可以提高施密特正交化过程的稳定性 | 列线性相关或者近似相关 |
施密特正交化在很多地方都有应用,这里只讨论与 Q R QR QR 有关的话题。对一个矩阵执行施密特正交化事实上就是在求取 Q R QR QR 分解中的 Q Q Q 矩阵,因为正交矩阵 Q Q Q 的特殊性,可以很轻松的通过 A A A 与正交矩阵 Q Q Q 求得 R R R 矩阵。
对于上三角矩阵,所有位于主对角线以下的元素必须为零;对于下三角矩阵,所有位于主对角线以上的元素必须为零。主对角线是否为零与是否为上下三角没有直接关系。
Q R QR QR 求解线性方程组有哪些帮助?
- 节省空间;
- 具有数值稳定性;
- 解无解方程;
我并不认为 Q R QR QR 分解相对于直接求解 A A A 的逆有更高的效率。考虑线性方程组 A x = b Ax=b Ax=b :
A x = b ⇒ Q R x = b ⇒ R x = Q T b Ax=b\Rightarrow QRx=b\Rightarrow Rx=Q^Tb Ax=b⇒QRx=b⇒Rx=QTb
令 y = Q T b y=Q^Tb y=QTb,有些人就下以下结论:对于不同的 b b b 我们只需要将其简单的乘以 Q T Q^T QT 再通过回代(Back substitution)就可以得到新的方程的解,而不需要重新计算 A − 1 A^{-1} A−1,事实上,我们也可以通过提前计算 A − 1 A^{-1} A−1 来避免求逆的过程。真正有意义的是:节省存储空间。 Q R QR QR 分解只需要存储一个列向量 Q T Q^T QT 和上三角矩阵(有很多零,可以不存储),而后者既要存储 A A A,还需要存储 A − 1 A^{-1} A−1;
2.1 Q R QR QR 分解有更好的数值稳定性
相对于高斯消元法, Q R QR QR 分解更具有数值稳定性。数值稳定性(Numerical Stability)是指数值算法在小的扰动下(如计算机的舍去误差)下,得到的解仍然是近似于真实的解。看一个具体的例子,说明这个数值稳定性概念:
考虑系数矩阵 A A A 和 结果向量 b b b 组成的线性方程组 A x = b Ax=b Ax=b 的解:
A = [ 1 1 1 1.0001 ] b = [ 2 2.0001 ] A=\begin{bmatrix}1&1\\1&1.0001\end{bmatrix} \quad b=\begin{bmatrix}2\\2.0001\end{bmatrix} A=[1111.0001]b=[22.0001]
容易得出: x = [ 1 1 ] x=\begin{bmatrix}1\\1\end{bmatrix} x=[11],当扰动作用于 b b b 变成 b ′ b' b′:
b ′ = [ 2 2 ] b'=\begin{bmatrix}2\\2\end{bmatrix} b′=[22]
这个解变成了 x ′ = [ 2 0 ] x'=\begin{bmatrix}2\\0\end{bmatrix} x′=[20],和原来的 x = [ 1 1 ] x=\begin{bmatrix}1\\1\end{bmatrix} x=[11] 相差甚远,尽管我们的扰动只是 0.0001 0.0001 0.0001。为什么我们说高斯消元法的数值稳定性差呢?高斯消元法会用到某一行的倍数减去另一个行,如果乘数是基于非常小的主元计算的,乘数会非常大,所有依赖这个乘数的元素的误差都会放大,而 Q R QR QR 分解的过程中,只涉及向量投影并不涉及高斯消元的小主元问题,所以我们说 Q R QR QR 分解具有比高斯消元法更大的数值稳定性。
2.2 计算对称三角矩阵的全部特征值
待补充
[1] https://programmersought.com/article/41251945673/
相关文章:

施密特正交化
相信大家在平时的期末考试中一定少不了对某某向量组执行标准正交化类型的题目。今天我们从这个题目入手,说明这个如何执行施密特正交化,以及为什么要进行正交化。 一、例子 例子:设 a 1 [ 1 2 − 1 ] a_1\begin{bmatrix}1\\2\\-1\end{bmat…...

低代码开发:加速应用开发的利器
目录 一、引言 二、低代码开发的定义和原理 三、低代码开发的关键特性和优势 四、低代码开发的应用场景 五、低代码开发平台的市场现状和发展趋势 六、成功案例分析 七、结论 一、引言 随着信息技术的快速发展,企业对于应用开发的需求也日益增长。传统的应用…...
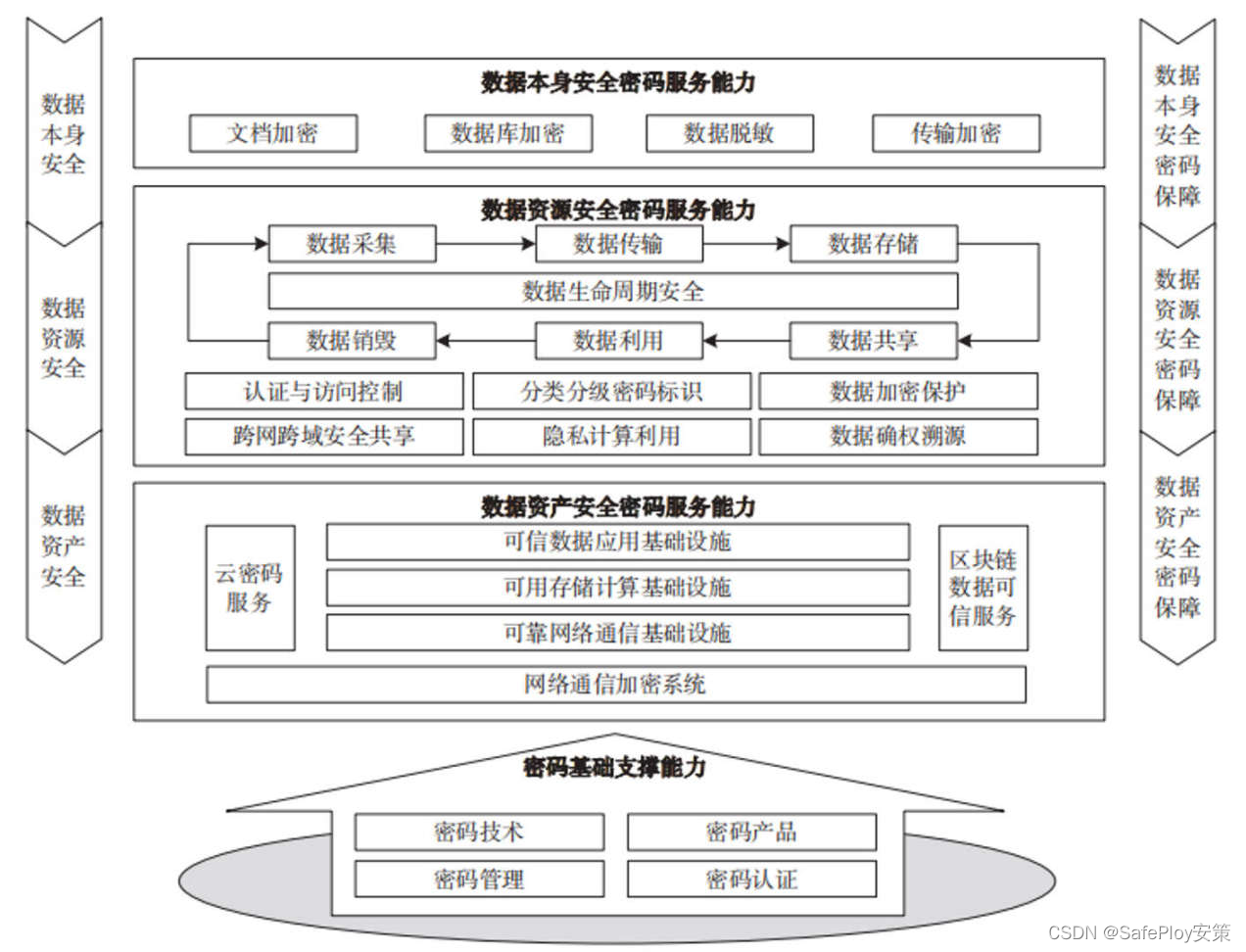
数据安全发展趋势与密码保护技术研究
随着数据跃升为新型生产要素,数据安全的内涵也从数据本身安全、数据资源安全,发展到数据资产安全三个层面提出了不同的要求,本文就是详细探讨数据安全的这三个层面的安全内容进行分析。 通过对数据安全不同发展阶段的安全需求和保障对象进行研…...

368周赛leetcode
1 2题元素和最小的山形三元组 经典动规 题目内容 给你一个下标从 0 开始的整数数组 nums 。 如果下标三元组 (i, j, k) 满足下述全部条件,则认为它是一个 山形三元组 : i < j < k nums[i] < nums[j] 且 nums[k] < nums[j] 请你找出 num…...

Vue 的 nextTick:深入理解异步更新机制
目录 一、前言 二、Vue.js 异步更新机制简述 三、Vue.nextTick原理 四、nextTick 的应用场景 1. 获取更新后的 DOM 元素 2. 在 DOM 更新后执行自定义的回调函数 3. 解决事件监听器中的更新问题 五、Vue.nextTick与其他异步更新方法的比较 六、总结 一、前言 Vue.js&a…...
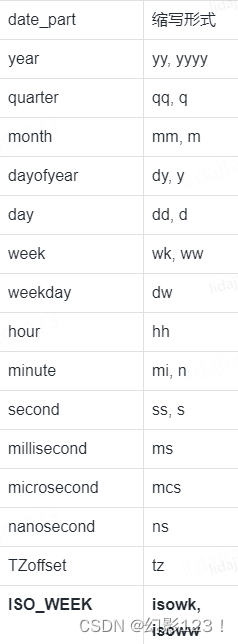
SQL关于日期的计算合集
前言 在SQL Server中,时间和日期是常见的数据类型,也是数据处理中重要的一部分。SQL Server提供了许多内置函数,用于处理时间和日期数据类型。这些函数可以帮助我们执行各种常见的任务,例如从日期中提取特定的部分,计…...

shell_44.Linux使用 getopt 命令
使用 getopt 命令 getopt 命令在处理命令行选项和参数时非常方便。它能够识别命令行参数,简化解析过程 1. 命令格式 getopt 命令可以接受一系列任意形式的命令行选项和参数,并自动将其转换成适当的格式。 getopt 的命令格式如下: getopt opt…...

Linux备份Docker的mysql数据并传输到其他服务器保证数据级容灾
目录 简介什么是容灾 ?容灾的分类容灾和备份有什么连系 ? 数据级容灾备份步骤1、scp命令:用于Linux之间复制文件和目录2、编写备份数据库脚本3、crontab定时任务执行脚本4、测试 应用级容灾业务级容灾 简介 为了防止客户系统的数据丢失&…...

【vue+nestjs】qq第三方授权登录【超详细】
项目场景: 前端使用vue3ts 后端使用nestjs 1.申请appId,appKey 1.进入qq互联官网。创建应用 特别注意 1.在填写网站回调域时,需要你线上真实能访问的。不然审核不通过。我的回调地址是前端路由地址 2.如果你想本地调试,回调到你的线上地址。你可以在本…...
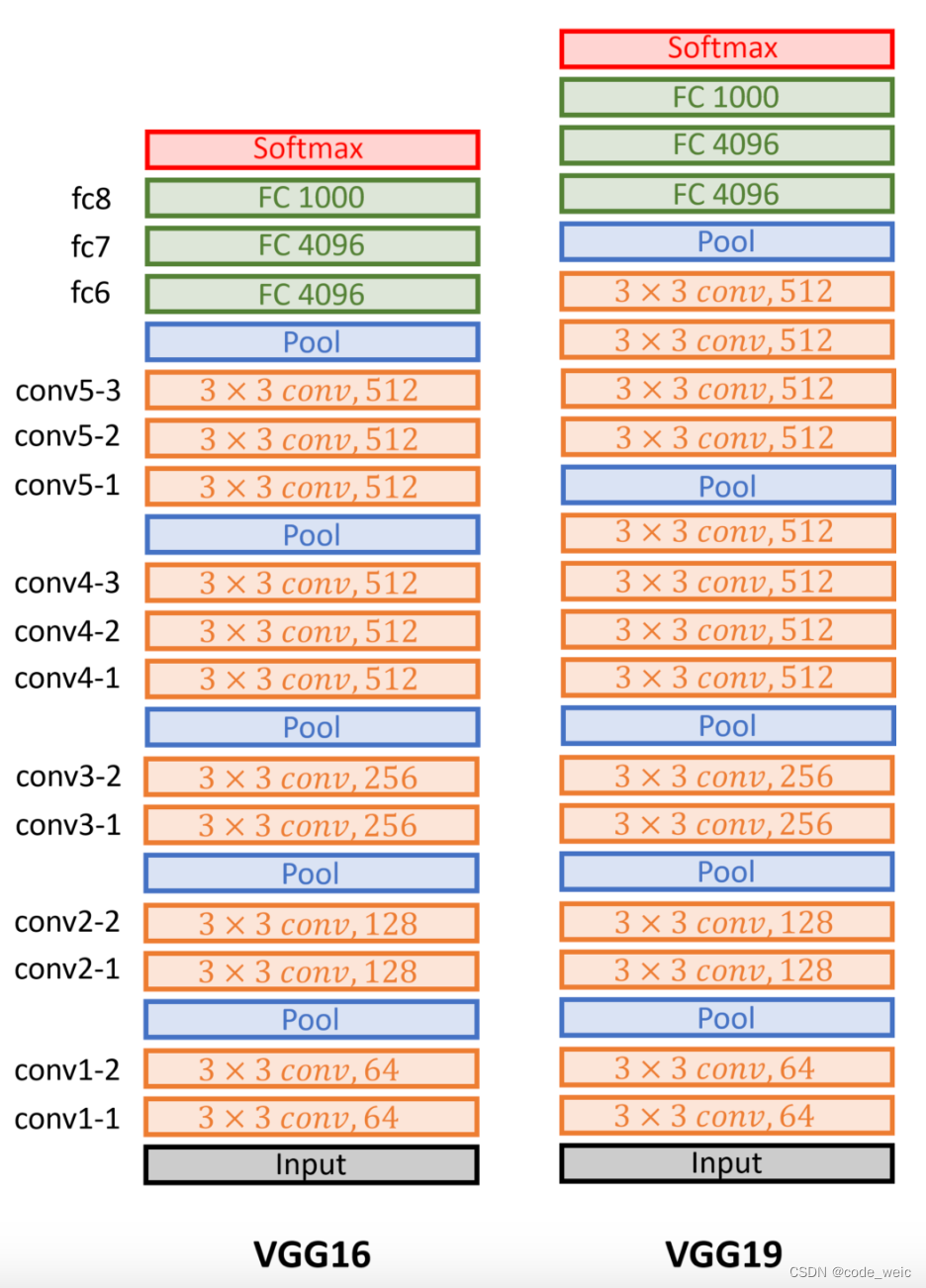
经典卷积神经网络 - VGG
使用块的网络 - VGG。 使用多个 3 3 3\times 3 33的要比使用少个 5 5 5\times 5 55的效果要好。 VGG全称是Visual Geometry Group,因为是由Oxford的Visual Geometry Group提出的。AlexNet问世之后,很多学者通过改进AlexNet的网络结构来提高自己的准确…...
/系统测试(ST)/用户验收测试(UAT))
系统集成测试(SIT)/系统测试(ST)/用户验收测试(UAT)
文章目录 单元测试集成测试系统测试用户验收测试黑盒测试白盒测试压力测试性能测试容量测试安全测试SIT和UAT的区别 单元测试 英文 unit testing,缩写 UT。测试粒度最小,一般由开发小组采用白盒方式来测试,主要测试单元是否符合“设计”。 …...

Android Gradle8.0以上多渠道写法以及针对不同渠道导入包的方式,填坑!
目录 多渠道的写法 针对多渠道引用不同的包 There was a failure while populating the build operation queue: Could not stat file E:\xxxx\xxxx\xxxx\app\src\UAT\libsUAT\xxx-provider(?)-xx.aar 最近升级了Gradle8.3之后,从Groovy 迁移到 Kotlinÿ…...
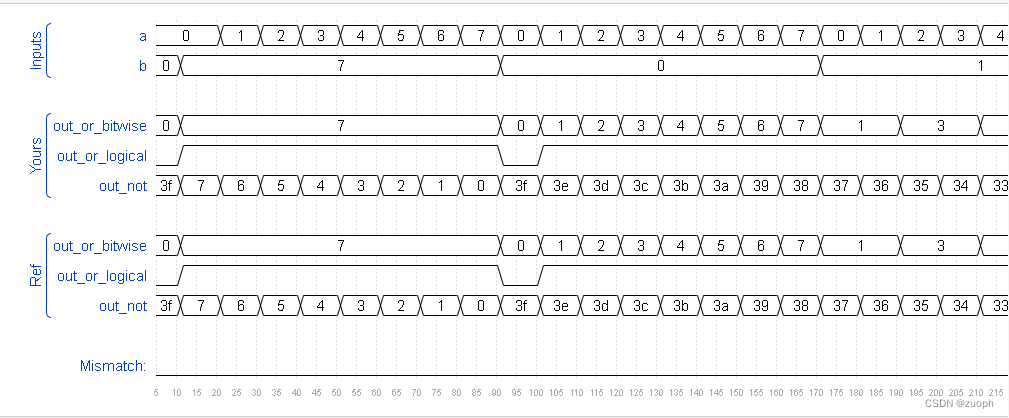
hdlbits系列verilog解答(向量门操作)-14
文章目录 一、问题描述二、verilog源码三、仿真结果 一、问题描述 构建一个具有两个 3 位输入的电路,用于计算两个向量的按位 OR、两个向量的逻辑 OR 以及两个向量的逆 (NOT)。将b反相输出到out_not上半部分,将a 的反相输出到out…...
)
工厂模式(初学)
工厂模式 1、简单工厂模式 是一种创建型设计模式,旨在通过一个工厂类(简单工厂)来封装对象的实例化过程 运算类 public class Operation { //这个是父类private double num1; //运算器中的两个值private double num2;public double getNu…...

python试题实例
背景: 在外地出差,突然接到单位电话,让自己出一些python考题供新人教育训练使用,以下是10道Python编程试题及其答案: 1.试题:请写一个Python程序,计算并输出1到100之间所有偶数的和。 答案&am…...
)
Java Heap Space问题解析与解决方案(InsCode AI 创作助手)
Heap Space问题是Java开发中常见的内存溢出问题之一,我们需要理解其原因和表现形式,然后通过优化代码、增加JVM内存和使用垃圾回收机制等方法来解决。 一、常见报错 java.lang.OutOfMemoryError: Java heap space二、Heap Space问题的原因 对象创建过…...
基于遥感影像的分类技术(监督/非监督和面向对象的分类技术)
遥感图像分类技术 “图像分类是将土地覆盖类别分配给像素的过程。例如,类别包括水、城市、森林、农业和草原。”前言 – 人工智能教程 什么是遥感图像分类? 遥感图像分类技术的三种主要类型是: 无监督图像分类监督图像分类基于对象的图像分析…...
 方法)
插入兄弟元素 insertAfter() 方法
insertAfter() 方法在被选元素后插入 HTML 元素。 提示:如需在被选元素前插入 HTML 元素,请使用 insertBefore() 方法。 语法 $(content).insertAfter(selector)例子: $("<span>Hello world!</span>").insertAfter(…...

【C++项目】高并发内存池第二讲中心缓存CentralCache框架+核心实现
CentralCache 1.框架介绍2.核心功能3.核心函数实现介绍3.1SpanSpanList介绍3.2CentralCache.h3.3CentralCache.cpp3.4TreadCache申请内存函数介绍3.5慢反馈算法 1.框架介绍 回顾一下ThreadCache的设计: 如图所示,ThreadCache设计是一个哈希桶结构&…...
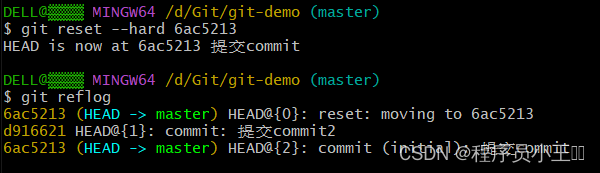
Git基础教程
一、Git简介 1、什么是Git? Git是一个开源的分布式版本控制系统,用于敏捷高效地处理任何或大或小的项目。 Git是Linus Torvalds为了帮助管理Linux内核开发而开发的一个开放源代码的版本控制软件。 Git与常用的版本控制工具CVS、Subversion等不同&#…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
