云台/稳定器/无人机姿态控制之欧拉角与四元数控制优缺点分析
基于欧拉角的姿态控制简述:
通过陀螺仪数据解算出姿态:pitch,roll,yaw(相对航向),根据目标 姿态:dst_pitch,dst_roll,dst_yaw计算出误差姿态pitch_err,roll_err,yaw_err。将误差姿态转换为目标速度e_pitch_rate,e_roll_rate,e_yaw_rate。然后再做坐标转换,变成基于机体坐标系的目标转速b_pitch_rate,b_roll_rate,b_yaw_rate。此后可以利用陀螺仪的角速度传感器做反馈控制了。
基于四元数的姿态控制简述:
通过陀螺仪数据解算出姿态四元数:q(q0,q1,q2,q3), 根据目标姿态(dst_pitch,dst_roll,dst_yaw 转换为四元数dst_q)四元数计算出误差四元数err_q。把误差四元数转换成目标速度e_rate_x,e_rate_y,e_rate_z。之后的做法和基于欧拉角的姿态控制一样了。
基于欧拉角的姿态控制的优点:
1.欧拉角容易理解,不论是开发者还是用户都能较为容易的理解,它们具有明确的物理意义,有于业务的实现和调试。
2. 欧拉角的每个角度都是独立解耦的,控制实现逻辑相对简单,如:云台/稳定器的跟随操作,俯仰角度只需要考虑跟随当前的俯仰电机运动即可。
3. 计算简单,不用牵涉矩阵/坐标旋转(业务逻辑),对MCU负担小,容易采用定点算法移植到低端MCU。
基于欧拉角的姿态控制的缺点
1.欧拉角有角度限制,俯仰角度在90°附近整个系统是不可靠的,虽然网上很多论文讨论全角度欧拉角算法,但这些算法的前提都是需要知道前一刻的角度再推算当前时刻的角度,实际应用不一定稳定。
2. 对于旋转类型的业务,如:非正交姿态(roll 不是 0° ,90°, 180°)情况的旋转实现较为复杂,如果:云台/稳定器的全跟随业务,要计算出目标姿态角比较麻烦。
基于四元数的姿态控制的优点:
1. 没有角度限制,可以表示机器的任意姿态。
2. 可以任意旋转目标姿态,对于各种旋转类型的业务实现非常简单,如:云台/稳定器的全跟随业务,只需要沿3个轴方向对目标姿态四元数进行旋转即可,实现起来简单快捷。
3. 几乎所有的业务运算都是四元数旋转和矩阵旋转,程序代码高效简洁,便于维护。
基于四元数的姿态控制的缺点:
1. 所有运算都是四元数旋转和矩阵计算,依赖于浮点运算,如果移植定点的话工作量巨大。所以对MCU有要求。不适合做低端产品。
2. 四元数姿态从数据上看没有物理意义,不利于业务调试。
3. 误差四元数一般取的是球面最短弧路径,对于无人机控制来说比较完美,但对于云台/稳定器来说,由于受限于电机限位(不可能3个电机都是360°无限位电机),需要做路径规划,这个就太麻烦了。
总结:
无人机姿态控制业务相对简单,而且可以处于任意姿态(暂态),所以无人机采用四元数控制是比较理想的。对于云台/稳定器来说,采用四元数控制需要仔细斟酌了,优点和缺点都很明显,且云台的业务逻辑比无人机要复杂很多,各种工作模式与姿态相互掺杂,如果采用四元数需要对四元数的旋转理解比较透彻才行。
相关文章:

云台/稳定器/无人机姿态控制之欧拉角与四元数控制优缺点分析
基于欧拉角的姿态控制简述: 通过陀螺仪数据解算出姿态:pitch,roll,yaw(相对航向),根据目标 姿态:dst_pitch,dst_roll,dst_yaw计算出误差姿态pitch_err,roll_err,yaw_err。将误差姿态转换为目标速度e_pitch_rate,e_roll_rate,e_yaw_rate。然后…...
:依赖管理神器)
Go 工具链详解(六):依赖管理神器
go mod 是 Golang 的官方依赖管理工具,从 Go 1.11 版本开始引入。go mod 使用一种被称为模块(modules)的方式来管理依赖,每个模块都包含了一组 Golang 包。一个 Go 程序可以由多个模块组成,每个模块都可以有自己的 go.…...

C语言解决约瑟夫环问题
约瑟夫环问题是一个经典的数学问题,它的描述如下:有n个人围成一圈,从第1个人开始报数,数到第m个人出列,然后从出列的下一个人开始重新报数,数到第m个人出列,如此循环,直到最后一个人…...
6.6 Elasticsearch(六)京淘项目改造
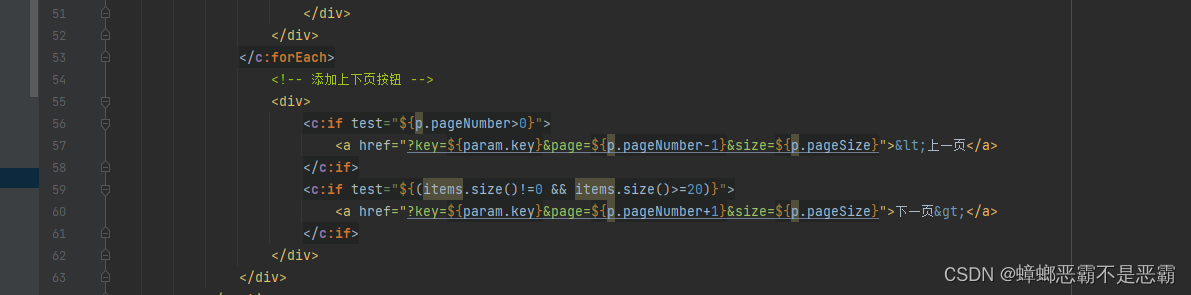
文章目录 1.项目准备2.基础配置2.1 添加pom.xml依赖2.2 yml配置es服务器地址列表 3.具体实现3.1 item实体类封装3.2 添加接口3.3 SearchController 4.search.jsp界面4.1 搜索内容展示4.2 高亮内容样式设置4.3 搜索框内容回填4.4 添加上下页按钮 1.项目准备 我们切换回到此前的…...

Socks5代理:数字化时代的技术支柱
随着数字化时代的到来,技术不仅改变了我们的日常生活,还重新定义了商业、通信、娱乐和全球互联。在这一浪潮中,Socks5代理技术崭露头角,成为跨界电商、爬虫数据分析、企业出海和游戏体验的关键推动力。这项技术不仅在实现数字化愿…...
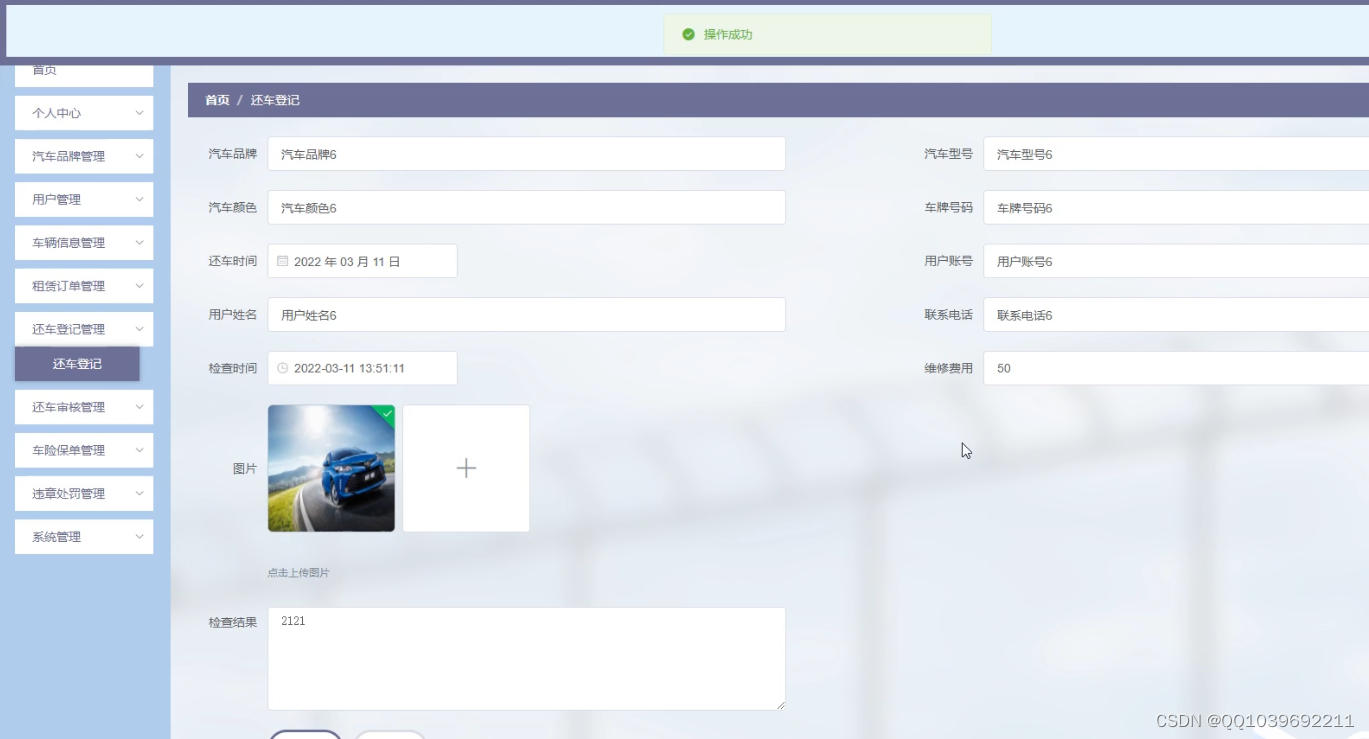
基本微信小程序的汽车租赁公司小程序
项目介绍 任何系统都要遵循系统设计的基本流程,本系统也不例外,同样需要经过市场调研,需求分析,概要设计,详细设计,编码,测试这些步骤,基于Java语言、微信小程序技术设计并实现了汽…...
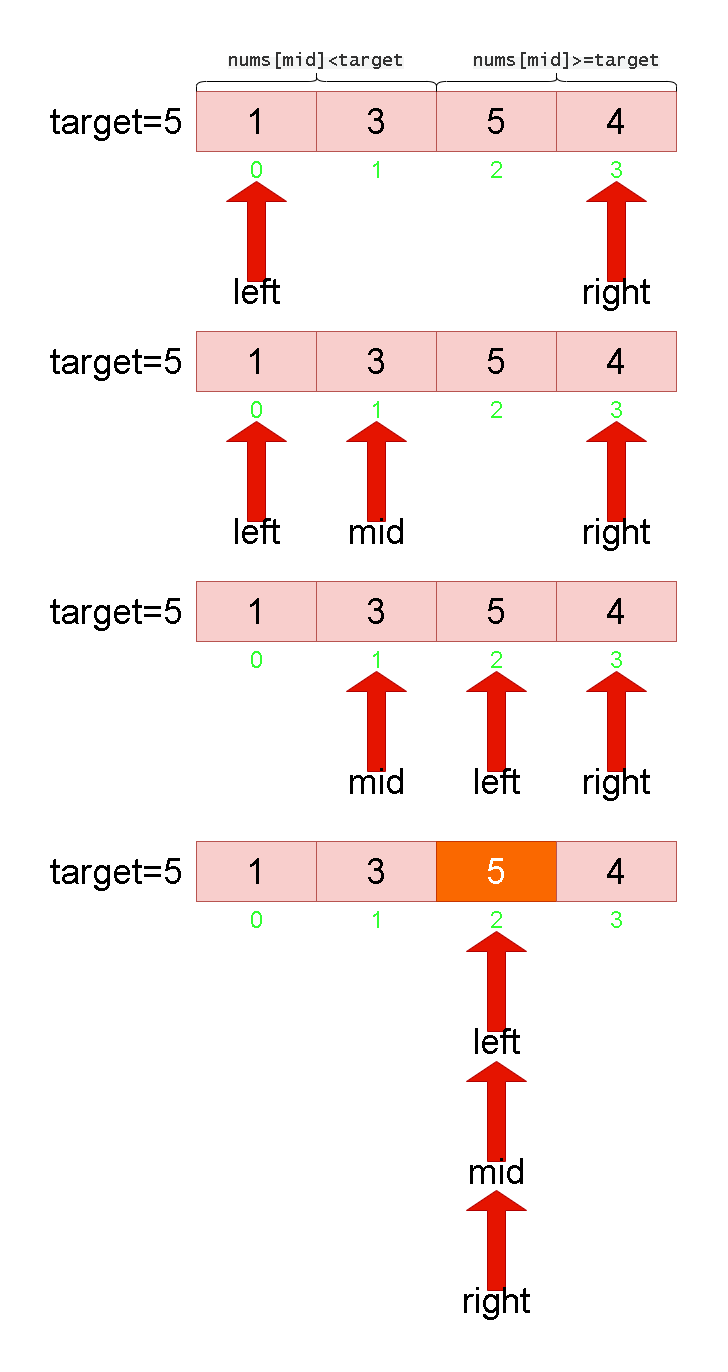
Leetcode刷题详解——搜索插入位置
1. 题目链接:35. 搜索插入位置 2. 题目描述: 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。…...

centos升级openssh
注意: openssh升级异常会造成服务失联,如果在允许的情况下可以安装talent服务,使用talent升级; 如果不能安装talent服务,可以打开多个终端,启动ping命令,防止升级终端失败后,作为备用…...

架构、框架、模式,极简文字介绍
1、架构、框架、模式是一种从大到小的关系,也是一种组合关系 2、架构一般针对一个行业或一类应用,是技术和应用的完美组合 3、框架比较小,很多表现为中间件,框架一般是从技术角度解决同类问题,从技术的横切面来解决实…...

Java实现Fisher‘s Exact Test 的置信区间的计算
实现代码 package com.bgi.aigi.common.utils;public class FisherExactUtils {public static double[] getConfidenceInterval(double[][] data) {if (datanull||data.length!2||data[0].length!2||data[1].length!2) {return null;}double[] intervalnew double[2];double …...
,即插即用,助力小目标检测 | NeurIPS2022)
YOLOv8改进:全网原创首发 | 新颖的多尺度卷积注意力(MSCA),即插即用,助力小目标检测 | NeurIPS2022
💡💡💡本文全网首发独家改进:多尺度卷积注意力(MSCA),有效地提取上下文信息,新颖度高,创新十足。 1)作为注意力MSCA使用; 推荐指数:五星 MSCA | 亲测在多个数据集能够实现涨点,多尺度特性在小目标检测表现也十分出色。 💡💡💡Yolov8魔术师,独家首发…...
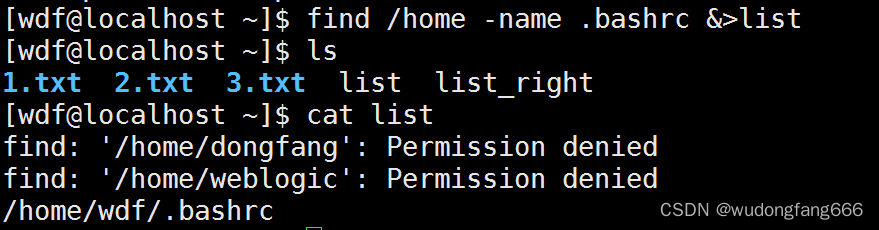
linux中好玩的数据流定向和管道命令一
知识点复习: 什么是数据流定向,个人理解就是将 一些结果信息不打印在屏幕上,而是定位在某一个文件里面 ll /wdf > file 会覆盖file的原内容 ll /wdf >> 会追加到原文件后面 比如在自己的目录新建1.TXT, 2.txt ll /…...

tesseract-ocr-w64-setup-5.3.3.20231005.exe 百度网盘下载
链接:https://pan.baidu.com/s/1q6u-nRvj2S8n6jSYz2iqig?pwdbtm4 提取码:btm4...

Linux环境下Redis 集群部署
Linux环境下Redis 集群部署 1.单机Redis部署2.Redis 集群配置2.1 创建redis集群安装目录2.2 将redis单机部署目录下的redis.confi文件复制到每个目录下2.3 修改每个文件夹下的redis.conf2.4 修改完六个配置内容后开始启动2.5 启动完后查看进程2.6 建集群 1.单机Redis部署 Linu…...

html iframe 框架有哪些优缺点?
目录 前言: 用法: 理解: 优点: 嵌套外部内容: 独立性: 分离安全性: 跨平台兼容性: 方便维护: 缺点: 性能开销: 用户体验问题…...

git 版本管理
标签管理 git tag: 标签的操作 用于给某次提交打个标签 命令:git tag B08P09 为当前提交打上 B08P09 的标签 命令:git tag B08P09 ab1591eb4e06c1e93fdd50126b9fab8a88d89155 为这个节点打上 B08P09 的标签 命令:git tag -a <tagname>…...

hyperf框架接入pgsql扩展包
文章目录 hyperf2.2安装 hyperf3.0安装 配置 环境版本支持 hyperf框架版本php版本database版本2.2>7.4~2.2.03.0>8.1~3.0.0 hyperf2.2 https://github.com/hyperf/database-pgsql-incubator 安装 hyperf/database 组件版本必须大于等于 v2.2.26 composer require hype…...
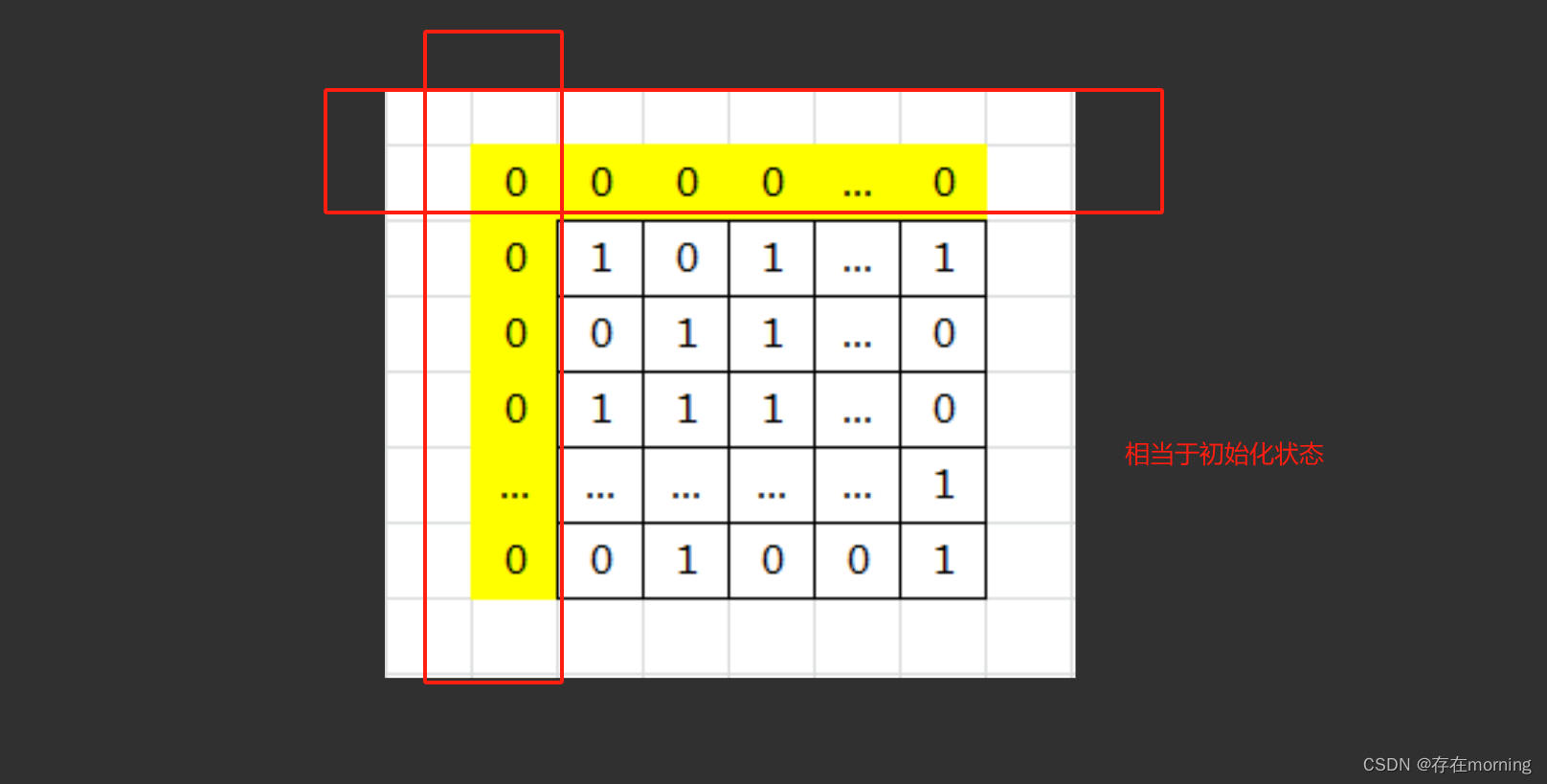
【算法训练-动态规划 五】【二维DP问题】最大正方形
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【动态规划】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...

20.Node-Express框架的用法
题记 node.js中express框架的用法 Express框架的特点 可以设置中间件来响应 HTTP 请求。 定义了路由表用于执行不同的 HTTP 请求动作。 可以通过向模板传递参数来动态渲染 HTML 页面。 安装Express模块 npm install express --save 安装重要模块 npm install body-parser --…...

cuda卸载
去查看你的电脑显卡对应的cuda版本,不然还是一整个用不到gpu的情况嘿嘿. 啊啊啊啊打开控制面板看一下,驱动不要乱卸载: 这些东西不能全部卸载了哦,只能卸载含有“CUDA”的那几个(其实其他的可能也没有用 但是不懂的哇 …...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
