Bayes决策:身高与体重特征进行性别分类
代码与文件请从这里下载:Auorui/Pattern-recognition-programming: 模式识别编程 (github.com)
简述
分别依照身高、体重数据作为特征,在正态分布假设下利用最大似然法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。在分类器设计时考察采用不同先验概率(如0.5对0.5, 0.75对0.25, 0.9对0.1等)进行实验,考察对决策规则和错误率的影响。
同时采用身高与体重数据作为特征,在正态分布假设下估计概率密度,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。 比较相关假设和不相关假设下结果的差异。在分类器设计时可以考察采用不同先验概率进行实验,考察对决策和错误率的影响。
最小错误率贝叶斯决策
这里要对男性和女性的数据进行分类,先要求解先验概念P(x),这个概率是通过统计得到的,或者依据自身依据经验给出的一个概率值,所以这个值是可以进行设定的,可选择0.5对0.5,0.75对0.25,0.9对0.1这些进行测试。
在贝叶斯统计中,后验概率是在考虑新信息之后事件发生的修正或更新概率。后验概率通过使用贝叶斯定理更新先验概率来计算。
其中为x的概率密度函数,即是:
贝叶斯决策可以使用下面的等式来等价表示为
如果满足上式条件,则x属于,否则就属于
,这个就是最小错误贝叶斯决策规则。
最小风险贝叶斯决策
在实际的应用中,分类错误率最小并不一定是最好的标准,不同类别的分类错误可能会导致不同的后果。有时,某些类别的错误分类可能比其他类别更为严重。例如,在医疗诊断中,将疾病误诊为健康可能比将健康误诊为疾病更为严重。在有决策风险时候,根据风险重新选择区域和
从而使得
最小。与
相关的风险或损失定义为:
对于本数据,只有两类:
若,则
属于
类,即有
再经过简化,当类的样本被错误的分类会产生更严重的后果,可设置为
,所以若
,则判定为
类。
数据预处理
首先我们可以观察我们的数据:

它大概是这样分布的,一行数据为身高和体重。你可以使用python文件按行读取进行数据清洗,这里可以直接使用np.loadtxt,它会返回一个二维的数组,使用切片的方法就能划分出身高和体重的特征并进行均值方差化。
# @Auorui
import numpy as np
from scipy.stats import normclass Datasets:# 一个简单的数据加载器def __init__(self, datapath, t):self.datapath = datapathself.data = np.loadtxt(self.datapath) # 二维数组self.height = self.data[:, 0]self.weight = self.data[:, 1]self.length = len(self.data)self.t = tdef __len__(self):return self.lengthdef mean(self, data):# 均值,可以使用np.mean替换total = 0for x in data:total += xreturn total / self.lengthdef var(self, data):# 方差,可以使用np.var替换mean = self.mean(data)sq_diff_sum = 0for x in data:diff = x - meansq_diff_sum += diff ** 2return sq_diff_sum / self.lengthdef retain(self, *args):# 保留小数点后几位formatted_args = [round(arg, self.t) for arg in args]return tuple(formatted_args)def __call__(self):mean_height = self.mean(self.height)var_height = self.var(self.height)mean_weight = self.mean(self.weight)var_weight = self.var(self.weight)return self.retain(mean_height, var_height, mean_weight, var_weight)数据加载
def Dataloader(maledata,femaledata):mmh, mvh, mmw, mvw = maledata()fmh, fvh, fmw, fvw = femaledata()male_height_dist = norm(loc=mmh, scale=mvh**0.5)male_weight_dist = norm(loc=mmw, scale=mvw**0.5)female_height_dist = norm(loc=fmh, scale=fvh**0.5)female_weight_dist = norm(loc=fmw, scale=fvw**0.5)data_dist = {'mh': male_height_dist,'mw': male_weight_dist,'fh': female_height_dist,'fw': female_weight_dist}return data_dist这里使用字典的方式存储男女数据的正态分布化。
计算概率密度函数(pdf值)以及贝叶斯决策
这里我们将会采用身高进行最小风险贝叶斯决策,采用体重进行最小错误率贝叶斯决策,采用身高、体重进行最小错误率贝叶斯决策。
def classify(height=None, weight=None, ways=1):"""根据身高、体重或身高与体重的方式对性别进行分类:param height: 身高:param weight: 体重:param ways: 1 - 采用身高2 - 采用体重3 - 采用身高与体重:return: 'Male' 或 'Female',表示分类结果"""# 先验概率的公式 : P(w1) = m1 / m ,样本总数为m,属于w1类别的有m1个样本。p_male = 0.5p_female = 1 - p_malecost_male = 0 # 预测男性性别的成本,设为0就是不考虑了cost_female = 0 # 预测女性性别的成本cost_false_negative = 10 # 实际为男性但预测为女性的成本cost_false_positive = 5 # 实际为女性但预测为男性的成本assert ways in [1, 2, 3], "Invalid value for 'ways'. Use 1, 2, or 3."assert p_male + p_female == 1., "Invalid prior probability, the sum of categories must be 1"# if ways == 1:# assert height is not None, "If mode 1 is selected, the height parameter cannot be set to None"# p_height_given_male = male_height_dist.pdf(height)# p_height_given_female = female_height_dist.pdf(height)### return 1 if p_height_given_male * p_male > p_height_given_female * p_female else 2if ways == 1:assert height is not None, "If mode 1 is selected, the height parameter cannot be set to None"p_height_given_male = male_height_dist.pdf(height)p_height_given_female = female_height_dist.pdf(height)risk_male = cost_male + cost_false_negative if p_height_given_male * p_male <= p_height_given_female * p_female else cost_femalerisk_female = cost_female + cost_false_positive if p_height_given_male * p_male >= p_height_given_female * p_female else cost_malereturn 1 if risk_male <= risk_female else 2if ways == 2:assert height is not None, "If mode 2 is selected, the weight parameter cannot be set to None"p_weight_given_male = male_weight_dist.pdf(weight)p_weight_given_female = female_weight_dist.pdf(weight)return 1 if p_weight_given_male * p_male > p_weight_given_female * p_female else 2if ways == 3:assert height is not None, "If mode 3 is selected, the height and weight parameters cannot be set to None"p_height_given_male = male_height_dist.pdf(height)p_height_given_female = female_height_dist.pdf(height)p_weight_given_male = male_weight_dist.pdf(weight)p_weight_given_female = female_weight_dist.pdf(weight)return 1 if p_height_given_male * p_weight_given_male * p_male > p_height_given_female * p_weight_given_female * p_female else 2return 3使用测试集验证并计算预测准确率
def test(test_path,ways=3):test_data = np.loadtxt(test_path)true_gender_label=[]pred_gender_label=[]for data in test_data:height, weight, gender = datatrue_gender_label.append(int(gender))pred_gender = classify(height, weight, ways)pred_gender_label.append(pred_gender)if pred_gender == 1:print('Male')elif pred_gender == 2:print('Female')else:print('Unknown\t')return true_gender_label, pred_gender_labeldef accuracy(true_labels, predicted_labels):assert len(true_labels) == len(predicted_labels), "Input lists must have the same length"correct_predictions = sum(1 for true, pred in zip(true_labels, predicted_labels) if true == pred)total_predictions = len(true_labels)accuracy = correct_predictions / total_predictionsreturn accuracy预测结果
采用身高进行最小风险贝叶斯决策
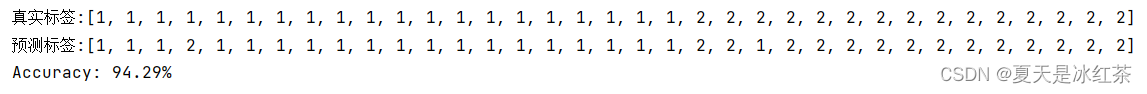
当采用身高进行最小风险贝叶斯决策,准确率在test1数据上的准确率为94.29%,在test2数据上的准确率为91.0%。
采用体重进行最小错误率贝叶斯决策

当采用体重进行最小风险贝叶斯决策,准确率在test1数据上的准确率为94.29%,在test2数据上的准确率为85.33%。
采用身高、体重进行最小错误率贝叶斯决策
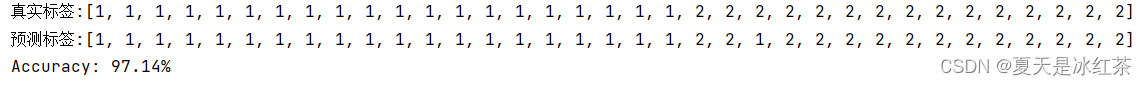
当采用身高、体重进行最小错误率贝叶斯决策,准确率在test1数据上的准确率为97.14%,在test2数据上的准确率为90.33%。
添加新的特征
除了身高、体重的组合,我们也可以延伸出新的特征,比如bmi。
def calculate_bmi(height,weight):# 计算BMI作为新特征height_meters = height / 100 # 将身高从厘米转换为米bmi = weight / (height_meters ** 2) # BMI计算公式return bmi这样能做出的特征就更多了,感兴趣的不妨沿着这个思路继续做。
相关文章:
Bayes决策:身高与体重特征进行性别分类
代码与文件请从这里下载:Auorui/Pattern-recognition-programming: 模式识别编程 (github.com) 简述 分别依照身高、体重数据作为特征,在正态分布假设下利用最大似然法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决…...

【考研数学】数学“背诵”手册 | 需要记忆且容易遗忘的知识点
文章目录 引言一、高数常见泰勒展开 n n n 阶导数公式多元微分函数连续、可微、连续可偏导之间的关系多元函数极值无条件极值条件极值 三角函数的积分性质华里士公式( “点火”公式 )特殊性质 原函数与被积函数的奇偶性结论球坐标变换公式 二、写在最后 …...
HJ3 明明的随机数
牛客网:HJ3 明明的随机数 https://www.nowcoder.com/practice/3245215fffb84b7b81285493eae92ff0?tpId37&tqId21226&ru/exam/oj 使用Go语言解题,最简单的方式: 解题一: // 运行时间:5ms 占用内存:…...
如何恢复u盘删除文件?2023最新分享四种方法恢复文件
U盘上删除的文件怎么恢复?使用U盘存储文件是非常方便的,例如:在办公的时候,会使用U盘来存储网络上查找到的资料、产品说明等。在学习的时候,会使用U盘来存储教育机构分享的教学视频、重点知识等。而随着U盘存储文件的概…...

8.稳定性专题
1. anr https://code84.com/303466.html 一句话,规定的时间没有干完要干的事,就会发生anrsystem_anr场景 input 5sservice 前台20s 后台60scontentprivider超市 比较少见 原因 主线程耗时 复杂layout iobinder对端block子线程同步锁blockbinder被占满导…...

基于51单片机的四种波形信号发生器仿真设计(仿真+程序源码+设计说明书+讲解视频)
本设计 基于51单片机信号发生器仿真设计 (仿真程序源码设计说明书讲解视频) 仿真原版本:proteus 7.8 程序编译器:keil 4/keil 5 编程语言:C语言 设计编号:S0015 这里写目录标题 基于51单片机信号发生…...
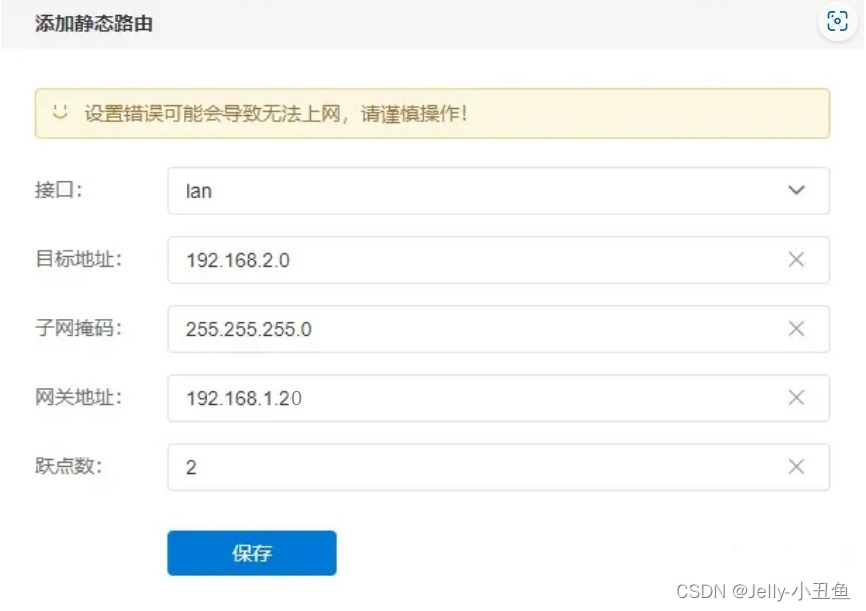
不同网段的IP怎么互通
最近在整理工作的时候发现一个不同网段无法互通的问题,就是我们大家熟知的一级路由和二级路由无法互通的问题。由于需要记录整个过程的完整性,这里也需要详细记录下整个过程,明白的人不用看,可以直接跳过,到解决方法去…...

C#序列化与反序列化详解
在我们深入探时C#序列化和反序列化,之前我们先要明白什么是序列化,它又称串行化,是.ET运行时环境用来支持用户定义 类型的流化的机制。序列化就是把一个对象保存到一个文件或数据库字段中去,反序列化就是在适当的时候把这个文件再…...
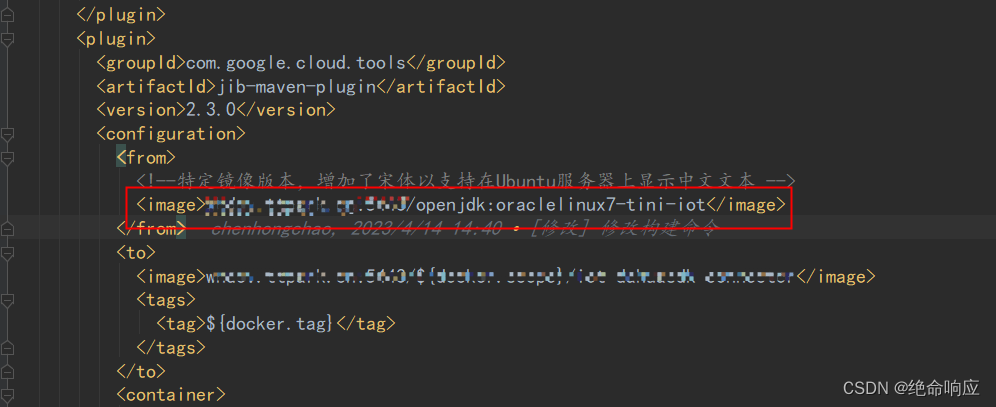
如何在k8s的Java服务镜像(Linux)中设置中文字体
问题描述:服务是基于springboot的Java服务,在项目上是通过Maven的谷歌插件打包,再由k8s部署的。k8s的镜像就是一个Java服务,Java服务用到了中文字体。 解决这个问题首先需要搞定镜像字体的问题。有很多类似的解决方案,…...

CT 扫描的 3D 图像分类-预测肺炎的存在
介绍 此示例将展示构建 3D 卷积神经网络 (CNN) 所需的步骤,以预测计算机断层扫描 (CT) 扫描中是否存在病毒性肺炎。2D CNN 通常用于处理 RGB 图像(3 通道)。3D CNN 就是 3D 的等价物:它以 3D 体积或一系列 2D 帧(例如 CT 扫描中的切片)作为输入,3D CNN 是学习体积数据表…...

整合管理案例题分析
本文摘自江山老师文档 五个过程 制定项目章程 1.没有写项目章程,没有颁布 2.项目经理自己颁布项目章程 3.项目经理修改项目章程 4.项目章程授权不够,项目经理没有权限,下面的人不听话 5.项目章程的内容不完整 制定项目管理计划 1.项目…...

mysql4
创建表并插入数据: 字段名 数据类型 主键 外键 非空 唯一 自增 id INT 是 否 是 是 否 primary key name VARCHAR(50) 否 否 是 否 否 not null glass VARCHAR(50) 否 否 是 否 否 not nullsch 表内容 id name glass 1 xiaommg glass 1 2 xiaojun …...
Python深度学习实战-基于tensorflow原生代码搭建BP神经网络实现分类任务(附源码和实现效果)
实现功能 前面两篇文章分别介绍了两种搭建神经网络模型的方法,一种是基于tensorflow的keras框架,另一种是继承父类自定义class类,本篇文章将编写原生代码搭建BP神经网络。 实现代码 import tensorflow as tf from sklearn.datasets import…...

PDF 文档处理:使用 Java 对比 PDF 找出内容差异
不论是在团队写作还是在个人工作中,PDF 文档往往会经过多次修订和更新。掌握 PDF 文档内容的变化对于管理文档有极大的帮助。通过对比 PDF 文档,用户可以快速找出文档增加、删除和修改的内容,更好地了解文档的演变过程,轻松地管理…...

压敏电阻有哪些原理?|深圳比创达电子EMC
压敏电阻是一种金属氧化物陶瓷半导体电阻器。它以氧化锌(ZnO)为基料,加入多种(一般5~10种)其它添加剂,经压制成坯体,高温烧结,成为具有晶界特性的多晶半导体陶瓷组件。氧化锌压敏电阻器的微观结构如下图1所示。 氧化锌…...

【计算机网络笔记】Web应用之HTTP协议(涉及HTTP连接类型和HTTP消息格式)
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...
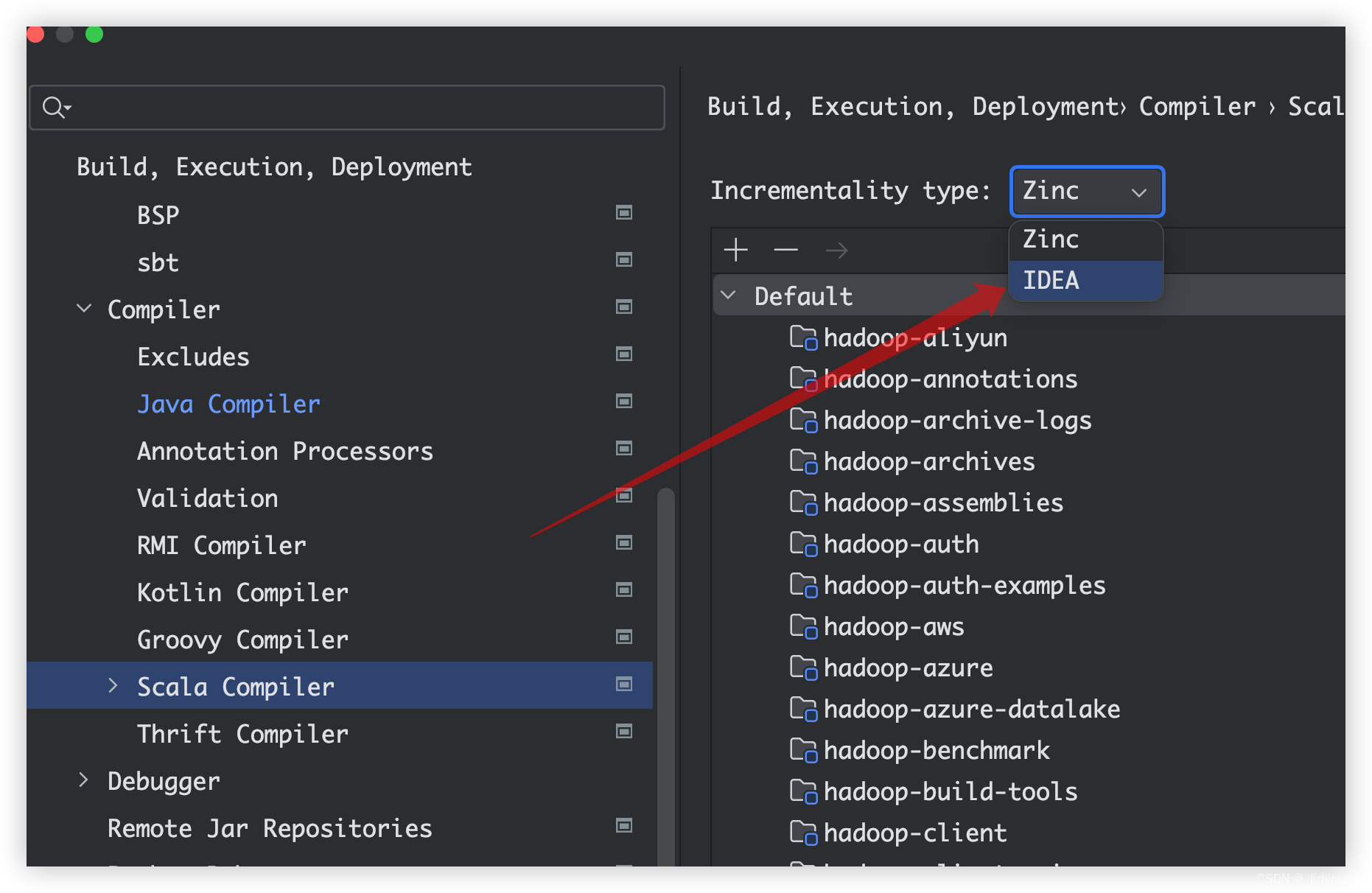
IDEA 2023.2.2 使用 Scala 编译报错 No scalac found to compile scala sources
一、问题 scala: No scalac found to compile scala sources 官网 Bug 链接 二、临时解决方案 Incrementality Type 先变成 IDEA 类型 Please go to Settings > Build, Execution, Deployment > Compiler > Scala Compiler and change the Incrementality type to …...

C51--PWN-舵机控制
PWM开发sg90舵机 1、简介 PWM(pulse width modulation)是脉冲宽度调制缩写。 通过对一系列脉冲的宽度进行调制,等效出所需要的波形(包含形状以及幅值)。对模拟信号电平进行数字编码,通过调节占空比的变化来…...

electron27+react18集成搭建跨平台应用|electron窗口多开
基于Electron27集成React18创建一个桌面端exe程序。 electron27-vite4-react18基于electron27结合vite4构建工具快速创建react18跨端应用实践。 版本列表 "vite": "^4.4.5" "react": "^18.2.0" "electron": "^27.0.1&…...
【k8s】kubeadm安装k8s集群
一、环境部署 master192.168.88.10docker、kubeadm、kubelet、kubectl、flannelnode01192.168.88.20docker、kubeadm、kubelet、kubectl、flannelnode02192.168.88.30docker、kubeadm、kubelet、kubectl、flannelhub.lp.com192.168.88.40 docker、docker-compose harbor-offli…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
