C#,数值计算——分类与推理,基座向量机(SVM,Support Vector Machines)的计算方法与源程序
把 Support Vector Machines 翻译成 支持向量机 是书呆子翻译。基座向量机 不好吗。
1 文本格式
using System;
namespace Legalsoft.Truffer
{
/// <summary>
/// Support Vector Machines
/// </summary>
public class Svm
{
private Svmgenkernel gker { get; set; }
private int m { get; set; }
private int fnz { get; set; }
private int fub { get; set; }
private int niter { get; set; }
private double[] alph { get; set; }
private double[] alphold { get; set; }
private Ran ran { get; set; } = null;
private bool alphinit { get; set; }
private double dalph { get; set; }
public Svm(Svmgenkernel inker)
{
this.gker = inker;
this.m = gker.y.Length;
this.alph = new double[m];
this.alphold = new double[m];
this.ran = new Ran(21);
this.alphinit = false;
}
public double relax(double lambda, double om)
{
int iter;
int j;
int jj;
int k;
int kk;
double sum;
double[] pinsum = new double[m];
if (alphinit == false)
{
for (j = 0; j < m; j++)
{
alph[j] = 0.0;
}
alphinit = true;
}
// alphold = alph;
alphold = Globals.CopyFrom(alph);
Indexx x = new Indexx(alph);
for (fnz = 0; fnz < m; fnz++)
{
if (alph[x.indx[fnz]] != 0.0)
{
break;
}
}
for (j = fnz; j < m - 2; j++)
{
k = (int)(j + (ran.int32() % (m - j)));
Globals.SWAP(ref x.indx[j], ref x.indx[k]);
}
for (jj = 0; jj < m; jj++)
{
j = x.indx[jj];
sum = 0.0;
for (kk = fnz; kk < m; kk++)
{
k = x.indx[kk];
sum += (gker.ker[j, k] + 1.0) * gker.y[k] * alph[k];
}
alph[j] = alph[j] - (om / (gker.ker[j, j] + 1.0)) * (gker.y[j] * sum - 1.0);
alph[j] = Math.Max(0.0, Math.Min(lambda, alph[j]));
if (jj < fnz && alph[j] > 0)
{
Globals.SWAP(ref x.indx[--fnz], ref x.indx[jj]);
}
}
Indexx y = new Indexx(alph);
for (fnz = 0; fnz < m; fnz++)
{
if (alph[y.indx[fnz]] != 0.0)
{
break;
}
}
for (fub = fnz; fub < m; fub++)
{
if (alph[y.indx[fub]] == lambda)
{
break;
}
}
for (j = fnz; j < fub - 2; j++)
{
k = (int)(j + (ran.int32() % (fub - j)));
Globals.SWAP(ref y.indx[j], ref y.indx[k]);
}
for (jj = fnz; jj < fub; jj++)
{
j = y.indx[jj];
sum = 0.0;
for (kk = fub; kk < m; kk++)
{
k = y.indx[kk];
sum += (gker.ker[j, k] + 1.0) * gker.y[k] * alph[k];
}
pinsum[jj] = sum;
}
niter = Math.Max((int)(0.5 * (m + 1.0) * (m - fnz + 1.0) / (Globals.SQR(fub - fnz + 1.0))), 1);
for (iter = 0; iter < niter; iter++)
{
for (jj = fnz; jj < fub; jj++)
{
j = y.indx[jj];
sum = pinsum[jj];
for (kk = fnz; kk < fub; kk++)
{
k = y.indx[kk];
sum += (gker.ker[j, k] + 1.0) * gker.y[k] * alph[k];
}
alph[j] = alph[j] - (om / (gker.ker[j, j] + 1.0)) * (gker.y[j] * sum - 1.0);
alph[j] = Math.Max(0.0, Math.Min(lambda, alph[j]));
}
}
dalph = 0.0;
for (j = 0; j < m; j++)
{
dalph += Globals.SQR(alph[j] - alphold[j]);
}
return Math.Sqrt(dalph);
}
public double predict(int k)
{
double sum = 0.0;
for (int j = 0; j < m; j++)
{
sum += alph[j] * gker.y[j] * (gker.ker[j, k] + 1.0);
}
return sum;
}
}
}
2 代码格式
using System;namespace Legalsoft.Truffer
{/// <summary>/// Support Vector Machines/// </summary>public class Svm{private Svmgenkernel gker { get; set; }private int m { get; set; }private int fnz { get; set; }private int fub { get; set; }private int niter { get; set; }private double[] alph { get; set; }private double[] alphold { get; set; }private Ran ran { get; set; } = null;private bool alphinit { get; set; }private double dalph { get; set; }public Svm(Svmgenkernel inker){this.gker = inker;this.m = gker.y.Length;this.alph = new double[m];this.alphold = new double[m];this.ran = new Ran(21);this.alphinit = false;}public double relax(double lambda, double om){int iter;int j;int jj;int k;int kk;double sum;double[] pinsum = new double[m];if (alphinit == false){for (j = 0; j < m; j++){alph[j] = 0.0;}alphinit = true;}// alphold = alph;alphold = Globals.CopyFrom(alph);Indexx x = new Indexx(alph);for (fnz = 0; fnz < m; fnz++){if (alph[x.indx[fnz]] != 0.0){break;}}for (j = fnz; j < m - 2; j++){k = (int)(j + (ran.int32() % (m - j)));Globals.SWAP(ref x.indx[j], ref x.indx[k]);}for (jj = 0; jj < m; jj++){j = x.indx[jj];sum = 0.0;for (kk = fnz; kk < m; kk++){k = x.indx[kk];sum += (gker.ker[j, k] + 1.0) * gker.y[k] * alph[k];}alph[j] = alph[j] - (om / (gker.ker[j, j] + 1.0)) * (gker.y[j] * sum - 1.0);alph[j] = Math.Max(0.0, Math.Min(lambda, alph[j]));if (jj < fnz && alph[j] > 0){Globals.SWAP(ref x.indx[--fnz], ref x.indx[jj]);}}Indexx y = new Indexx(alph);for (fnz = 0; fnz < m; fnz++){if (alph[y.indx[fnz]] != 0.0){break;}}for (fub = fnz; fub < m; fub++){if (alph[y.indx[fub]] == lambda){break;}}for (j = fnz; j < fub - 2; j++){k = (int)(j + (ran.int32() % (fub - j)));Globals.SWAP(ref y.indx[j], ref y.indx[k]);}for (jj = fnz; jj < fub; jj++){j = y.indx[jj];sum = 0.0;for (kk = fub; kk < m; kk++){k = y.indx[kk];sum += (gker.ker[j, k] + 1.0) * gker.y[k] * alph[k];}pinsum[jj] = sum;}niter = Math.Max((int)(0.5 * (m + 1.0) * (m - fnz + 1.0) / (Globals.SQR(fub - fnz + 1.0))), 1);for (iter = 0; iter < niter; iter++){for (jj = fnz; jj < fub; jj++){j = y.indx[jj];sum = pinsum[jj];for (kk = fnz; kk < fub; kk++){k = y.indx[kk];sum += (gker.ker[j, k] + 1.0) * gker.y[k] * alph[k];}alph[j] = alph[j] - (om / (gker.ker[j, j] + 1.0)) * (gker.y[j] * sum - 1.0);alph[j] = Math.Max(0.0, Math.Min(lambda, alph[j]));}}dalph = 0.0;for (j = 0; j < m; j++){dalph += Globals.SQR(alph[j] - alphold[j]);}return Math.Sqrt(dalph);}public double predict(int k){double sum = 0.0;for (int j = 0; j < m; j++){sum += alph[j] * gker.y[j] * (gker.ker[j, k] + 1.0);}return sum;}}
}
相关文章:

C#,数值计算——分类与推理,基座向量机(SVM,Support Vector Machines)的计算方法与源程序
把 Support Vector Machines 翻译成 支持向量机 是书呆子翻译。基座向量机 不好吗。 1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// Support Vector Machines /// </summary> public class Svm { priv…...

面试总结之消息中间件
RabbitMQ的消息如何实现路由 RabbitMQ是一个基于AMQP协议实现的分布式消息中间件,AMQP具体的工作机制是生产者将消息发送到RabbitMQ Broker上的Exchange交换机上,Exchange交换机将收到的消息根据路由规则发给绑定的队列(Queue)&am…...

Java零基础入门-逻辑运算符
前言 Java是一种广泛应用的编程语言,在在这里插入代码片软件开发中有着重要的地位。本文将介绍Java中的逻辑运算符及其在程序设计中的应用,希望能够帮助零基础的读者更好地入门学习Java。 摘要 本文将介绍Java中的三种逻辑运算符:与运算符…...

图的应用3.0-----拓扑排序
目录 前言 AOE网 1.相关概念 2.AOE网特征 拓扑排序 1.基本概念 2.方法步骤 3.拓扑排序的应用 拓扑排序代码实现 1.邻接矩阵的代码 2.邻接表代码 前言 今天我们学习图的应用----拓扑排序,说到排序,你们是不是会想到冒泡排序,插入排序…...

Unity之ShaderGraph如何实现冰冻效果
前言 今天我们来实现一个冰冻的效果,非常的炫酷哦。 如下图所示: 主要节点 Voronoi:根据输入UV生成 Voronoi 或Worley噪声。Voronoi 噪声是通过计算像素和点阵之间的距离生成的。通过由输入角度偏移控制的伪随机数偏移这些点,可以生成细胞簇。这些单元的规模以及产生的…...
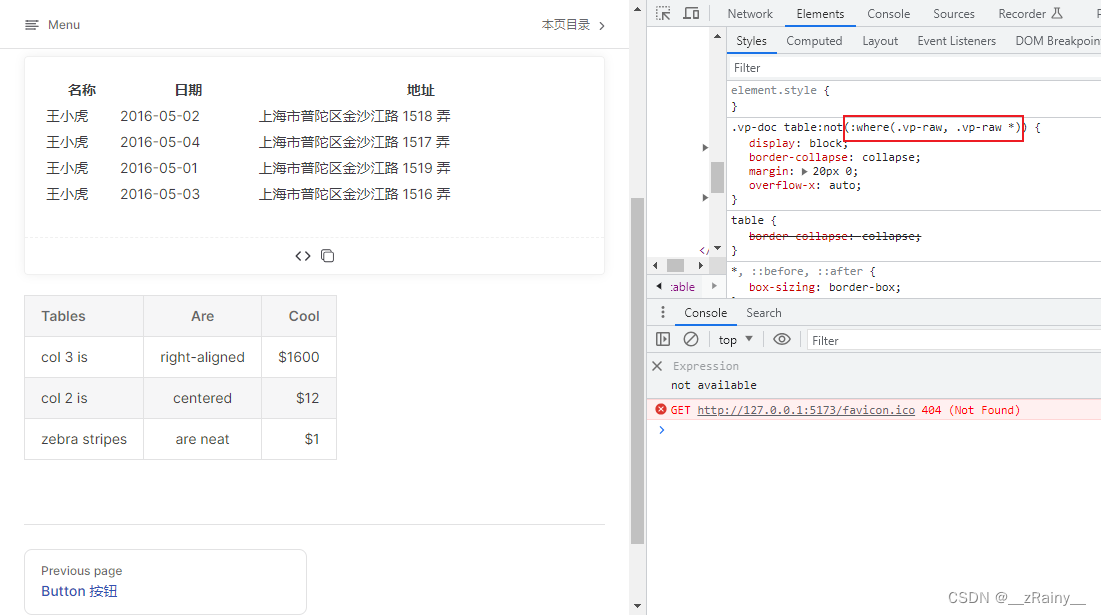
解决 viteprees 中 vp-doc 内置样式影响组件预
解决 viteprees 中 vp-doc 样式影响组件预览 问题 当使用"vitepress": "1.0.0-rc.22"作为组件库文档时,会自动引入vitepress的默认主题, 其中vp-doc中有大量的html标签样式 ... .vp-doc table {display: block;border-collapse: …...

flask 和fastdeploy 快速部署 yolov3
服务端 from flask import Flask,request,render_template from flask import session,redirect,jsonify import cv2 import numpy as np import base64 import os import fastdeploy as fd import datetime,timeapp=Flask(__name__)from logging import config,getLogger lo…...
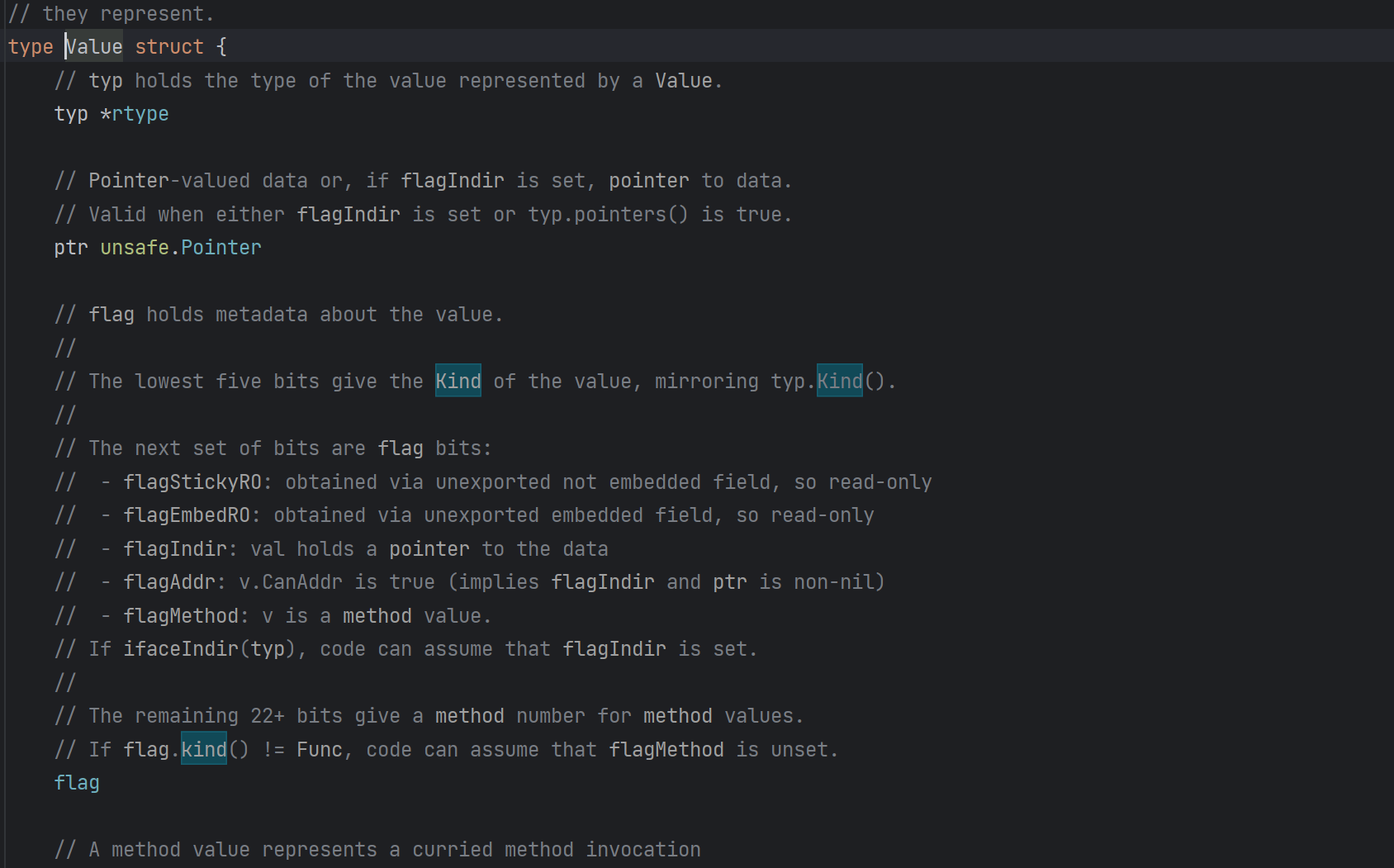
Go 反射
文章目录 获取类型和值获取属性的类型和值通过反射修改值获取方法的名称和类型调用方法反射的缺点 获取类型和值 之前讲过接口nil不一定等于空接口,因为一个 interface 底层 由 type value 构成,只有 type 和 value 都匹配,才能 reflect.Vl…...

竞赛选题 深度学习卷积神经网络垃圾分类系统 - 深度学习 神经网络 图像识别 垃圾分类 算法 小程序
文章目录 0 简介1 背景意义2 数据集3 数据探索4 数据增广(数据集补充)5 垃圾图像分类5.1 迁移学习5.1.1 什么是迁移学习?5.1.2 为什么要迁移学习? 5.2 模型选择5.3 训练环境5.3.1 硬件配置5.3.2 软件配置 5.4 训练过程5.5 模型分类效果(PC端) 6 构建垃圾…...

ts-node模块
ts-node模块 是一个非官方的npm模块,可以直接运行JS代码。 安装: npm install -g ts-node使用: ts-node script.ts如果不安装ts-node,可以通过npx在线调用ts-node,运行ts脚本。 npx ts-node script.ts...
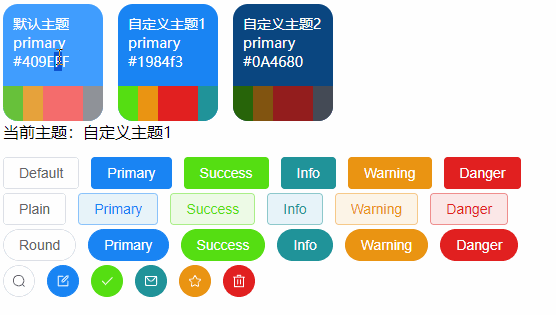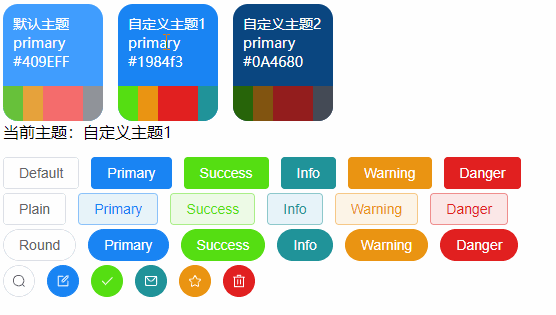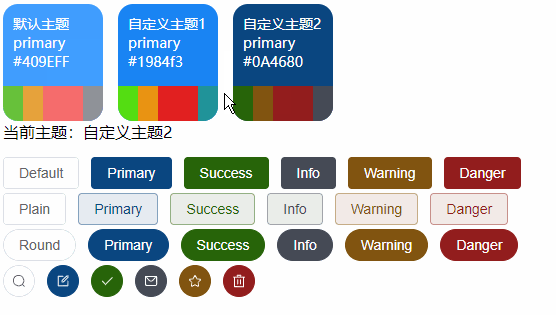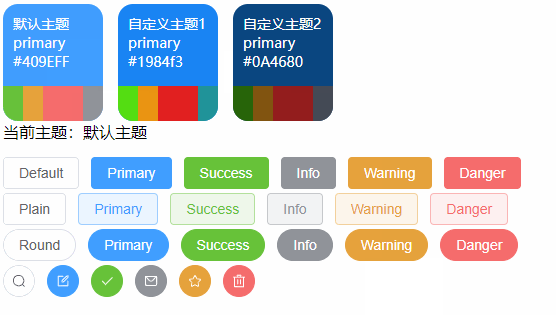
【VUE】ElementPlus之动态主题色调切换(Vue3 + Element Plus+Scss + Pinia)
前言 关于ElementPlus的基础主题色自定义可以参阅《【VUE】ElementPlus之自定义主题样式和命名空间》 有了上面基础的了解,我们知道ElementPlus的主题色调是基于CSS3变量特性进行全局控制的, 那么接下来我们也基于CSS3变量来实现主题色调的动态切换效果&…...
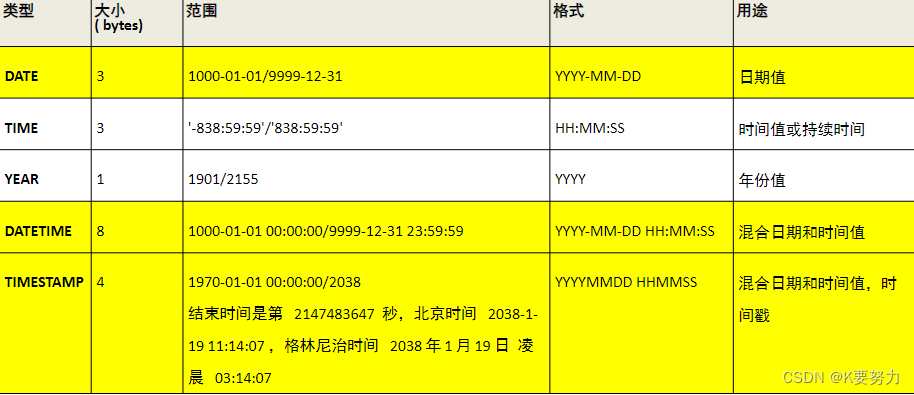
MySQL数据库基本操作1
文章目录 主要内容一.DDL1.创建表代码如下(示例): 2.创建表的类型3.其他操作4.修改表结构格式代码如下(示例): 二.DML1.数据插入代码如下(示例): 2.数据修改代码如下(示例): 3.数据删…...
Webpack简介及打包演示
Webpack 是一个静态模块打包工具,从入口构建依赖图,打包有关的模块,最后用于展示你的内容 静态模块:编写代码过程中的,html,css, js,图片等固定内容的文件 打包过程,注…...

面向对象设计模式——命令模式
命令设计模式(Command Pattern)是一种行为型设计模式,它的主要目的是将请求或操作封装成一个对象,从而允许参数化客户端对象,队列请求,将请求记录到日志,以及支持可撤销的操作。命令模式将请求的发出者(调用者)与请求的接收者(执行者)解耦,这使得系统更加灵活、可扩…...

selenium测试框架快速搭建(ui自动化测试)
一、介绍 selenium目前主流的web自动化测试框架;支持多种编程语言Java、pythan、go、js等;selenium 提供一系列的api 供我们使用,因此在web测试时我们要点页面中的某一个按钮,那么我们只需要获取页面,然后根据id或者n…...

TypeScript中的类型映射
类型映射 1. 简介 映射就是将一种类型按照映射规则,转成另一种类型,通常用于对象类型。 这里类型B通过A采用属性名索引的写法,完成了类型B的定义 type A {foo: number;bar: number; };type B {[prop in keyof A]: string; };这里复制了一…...

系统平台同一网络下不同设备及进程数据通讯--DDS数据分发服务中间件
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言(1)中间件的介绍(2)DDS介绍(3)发布者(4)订阅者(5)idl文件(定义msg结构体)(6)QoS(Quality of Service)策略(7)DDS测试工具介绍(…...

golang小技巧
1/有时需要把json内容返回给前段进行文本编辑json字段,那么最好是能返回格式化后的json,这样对于用户编辑页方便。这时候可以利用json.MarshalIndent(data, "", "\t")来进行格式化,带有缩进的marshal。 2/对holders的填…...

JavaWeb——IDEA操作:Project最终新建module
在project中创建新的module: 创建一个新的module很容易,但是它可能连接不上Tomcat,因此需要修改一些配置: 将以下地址修改为新module的地址...

前端开发技术栈(工具篇):2023深入了解webpack的安装和使用以及核心概念和启动流程(详细) 63.3k stars
目录 Webpack简介 Entry Module Chunk Loader Plugin Output Webpack的启动流程 Webpack的优缺点 Webpack的使用 1. 安装Webpack 2. 创建Webpack配置文件 3. 编写代码 4. 运行Webpack 5. 在HTML中引入打包后的文件 6. 执行编译命令 Webpack其他功能介绍 1. 使…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
