数据结构介绍与时间、空间复杂度
数据结构介绍
- 什么是数据结构?
- 什么是算法?
- 数据结构和算法的重要性
数据结构定义
数据结构是计算机科学中研究数据组织、存储和管理的一门学科。数据结构描述了数据对象之间的关系,以及对数据对象进行操作的方法和规则。
常见的数据结构
数组(Array):连续存储相同类型的数据元素。 链表(Linked
List):通过指针链接的节点组成,每个节点包含数据和指向下一个节点的指针。 栈(Stack):遵循后进先出(LIFO)原则的数据结构。
队列(Queue):遵循先进先出(FIFO)原则的数据结构。 树(Tree):由节点和边组成的层次结构,如二叉树、二叉搜索树等。
图(Graph):由节点和边组成的非线性数据结构,用于表示对象之间的关系。 哈希表(Hash
Table):使用哈希函数将键映射到存储位置的数据结构。 堆(Heap):特殊的树形数据结构,具有优先级队列的特性。
集合(Set):存储唯一元素的无序集合。 字典(Dictionary):存储键-值对的数据结构,也被称为映射或关联数组。
每种数据结构都有其特定的用途和适用场景。选择合适的数据结构可以提高算法的效率和性能。在实际应用中,通常会根据问题的需求选择合适的数据结构进行数据的组织和管理。
算法定义
算法是一组解决问题步骤的有限序列,它是为解决一个或多个计算问题而设计的明确指令集。简单来说,算法就是解决问题的方法和步骤。
算法由若干基本操作组成,包括数学运算、比较、赋值、条件分支和循环等,可以用自然语言、流程图、伪代码或编程语言来描述。
算法的设计和分析是计算机科学中的重要问题。有效的算法可以使问题的解决更为高效、精确和可靠。算法的时间复杂度和空间复杂度是评估算法效率和性能的主要指标,通常使用大 O 表示法来表示。
除了计算、搜索、排序和存储等常见的算法领域,还有许多其他领域,如人工智能、机器学习、图像处理和自然语言处理等,都使用了不同类型的算法来解决不同类型的问题。
总之,算法是计算机科学中不可或缺的组成部分,它们已经在各行各业中得到了广泛的应用。
算法特性
算法的特性包括以下几个方面:
有限性:任何一个算法都必须在有限的时间内停止。也就是说,算法的执行时间必须是有限的,否则算法就不能被执行。
确定性:算法的每个步骤必须被精确定义。也就是说,给定一个输入,程序每一次运行的结果是一样的。
可行性:算法必须可以在计算机或其他计算设备上实现。也就是说,算法中用到的所有操作都可以被计算机执行。
输入:算法必须有零个或多个输入,这些输入是要为问题提供解决方案的数据。
输出:算法必须有一个或多个输出,这些输出是算法为解决问题创建的解决方案。
可读性:算法必须易于理解和实现,可读性是评估算法质量的重要标准之一。
高效性:算法的执行结果必须是准确的,同时也要在可接受的时间内获得结果。算法的时间复杂度和空间复杂度通常用于评估算法的效率。
总之,算法是计算机科学中非常重要的概念和实践,对于计算机科学专业的学生和从事计算机编程工作的人员来说,掌握算法的设计和分析是非常必要的。
数据结构的重要性
数据结构和算法是计算机科学中最基础和最重要的两个领域。它们的作用体现在以下几个方面:
提高程序效率和性能:数据结构和算法可以有效地提高程序的效率和性能,使程序更加快速、可靠和节省资源。对于大量处理数据和计算密集型任务的程序,优秀的数据结构和算法非常重要。
最优解决方案:数据结构和算法是解决计算机科学中一系列问题的关键工具,例如搜索、排序、图形处理、人工智能和机器学习等各个领域。通过使用最优算法和数据结构,可以得到最优解决方案,从而提高计算机程序的效率和准确性。
简化复杂问题:许多计算机科学问题都是很复杂的,但是如果正确地应用数据结构和算法,可以使这些复杂问题变得更加简单。通过抽象和组织问题,使用正确的算法和数据结构,可以将问题简化为较小的子问题,从而更容易地解决问题。
促进创新:数据结构和算法的不断发展推动了计算机科学领域的创新,为各种领域提供了新的技术和工具。例如,人工智能、机器学习和大数据等领域的发展都离不开优秀的数据结构和算法的支持。
增强竞争力:掌握数据结构和算法对于计算机科学专业的学生和从事编程工作的人员来说非常重要,这是增强个人竞争力和就业竞争力的基础。人才市场对于掌握数据结构和算法方面的专业人才的需求量日益增大。
因此,学习和掌握数据结构和算法,对于计算机科学相关领域的学生和从业人员来说都非常重要,这是进入计算机行业、提高个人技能水平的基础。
时间复杂度
1.算法效率
2.时间复杂度
算法效率
如何衡量一个算法的好坏呢?
比如对于以下斐波那契数列:
long long Fib(int N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
我们可以知道这样用递归的方式实现斐波那契数列十分的简单,但是一旦数值稍微大了起来,就会因为递归开辟了许多函数空间,超过某一定值就会导致栈区溢出,对于该代码函数的实现和释放其实十分像古代帝位传承(嫡长子继承制)。
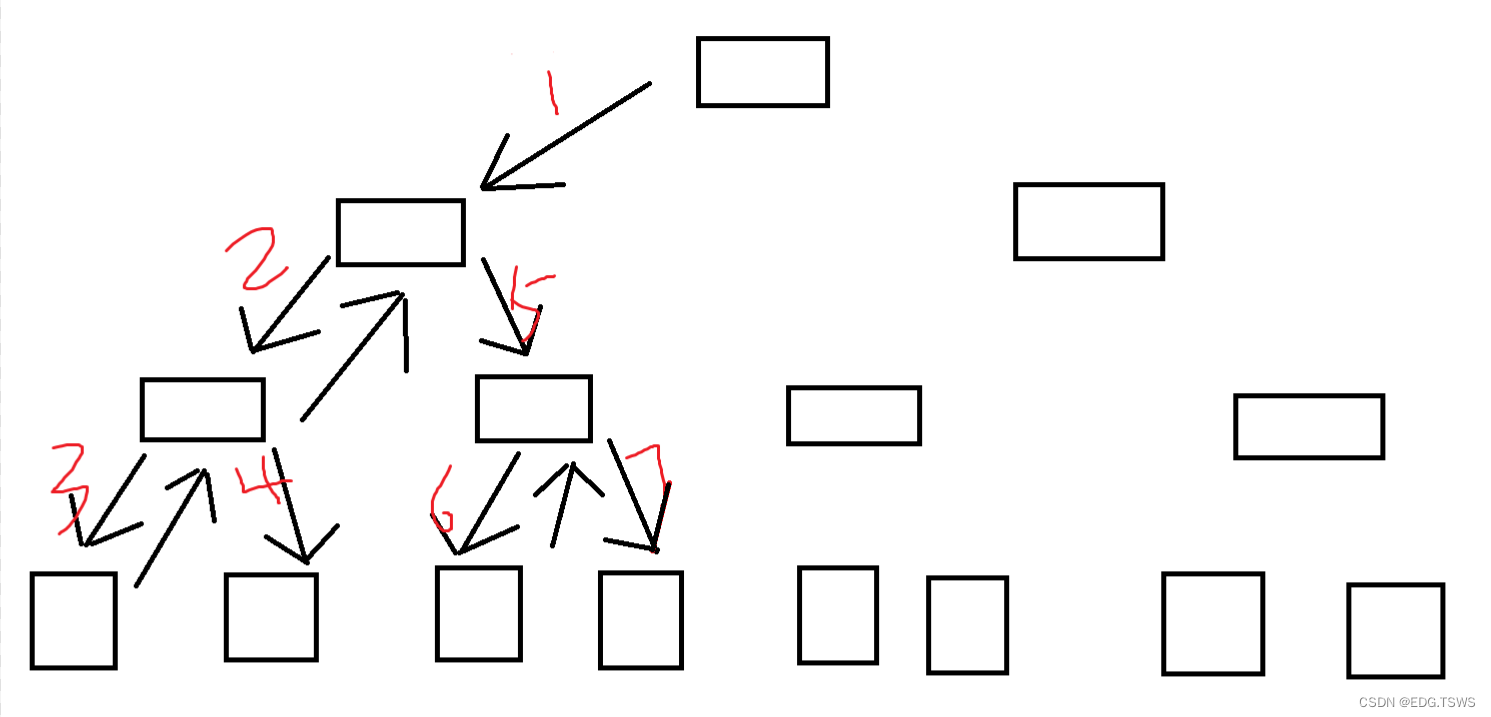
上面可以抽象成以递归方式实现的斐波那契数列,作者个人觉得还是十分像古代帝位的传承
斐波那契数列的递归实现方式非常简洁,但简洁一定好吗?那该如何衡量其好与坏呢?
算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
时间复杂度
时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}
printf("%d\n", count);
}
可以很简单的知道fun1中++count被执行了:n^2+2*n+10次。
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况: 任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)。
所以,Func1的时间复杂度为:O(n^2)。
空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
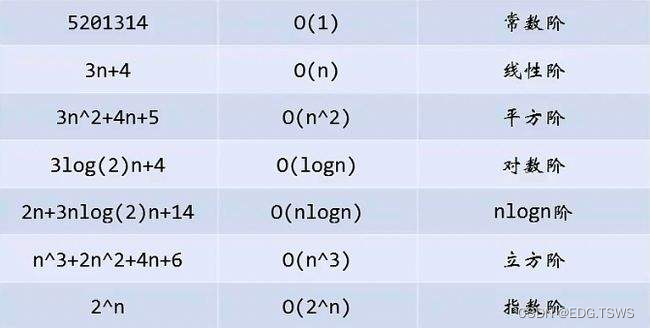
常见复杂度表
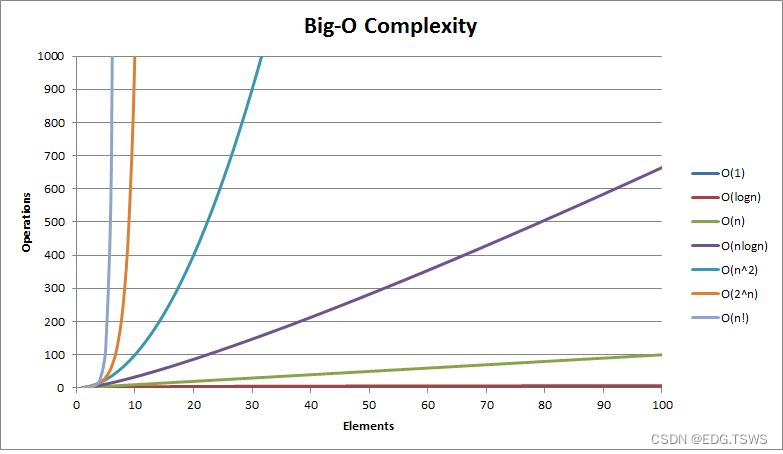
本篇内容到此为止,带大家简单认识了数据结构以及数据结构中时间、空间复杂度的理解,谢谢大家。
相关文章:

数据结构介绍与时间、空间复杂度
数据结构介绍 什么是数据结构?什么是算法?数据结构和算法的重要性 数据结构定义 数据结构是计算机科学中研究数据组织、存储和管理的一门学科。数据结构描述了数据对象之间的关系,以及对数据对象进行操作的方法和规则。 常见的数据结构 数…...
(c语言进阶)字符串函数、字符分类函数和字符转换函数
一.求字符串长度 1.strlen() (1)基本概念 头文件:<string.h> (2)易错点:strlen()的返回值为无符号整形 #include<stdio.h> #include<string.h> int main() {const char* str1 "abcdef";const char* str2 "bbb&q…...
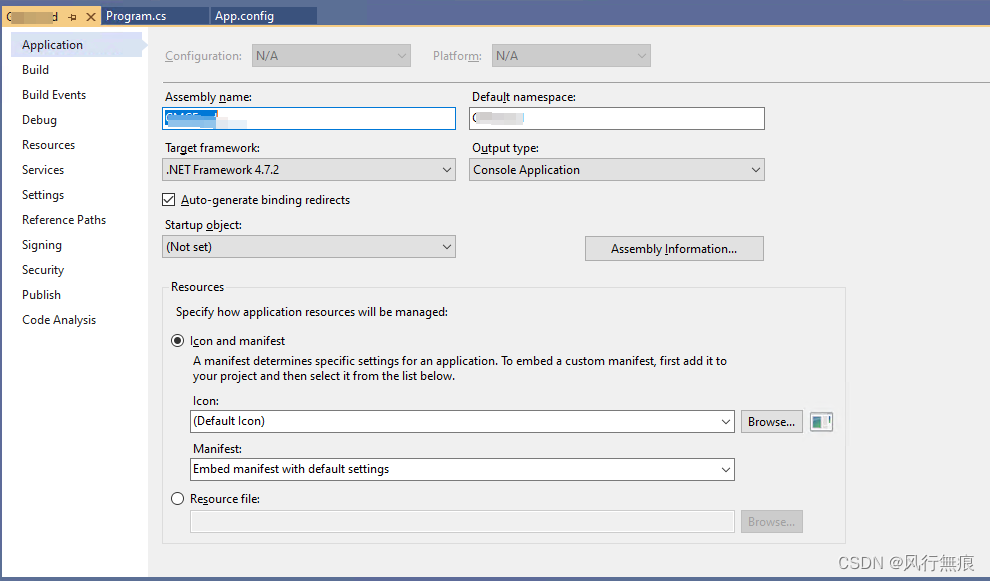
解决MySQL大版本升级导致.Net(C#)程序连接报错问题
数据库版本从MySQL 5.7.21 升级到 MySQL8.0.21 数据升级完成后,直接修改程序的数据库连接配置信息 <connectionStrings> <add name"myConnectionString" connectionString"server192.168.31.200;uidapp;pwdFgTDkn0q!75;databasemail;&q…...

Java 将对象List转为csv文件并上传远程文件服务器实现方案
问题情景: 最近项目中遇到了根据第三方系统传递过来的参数,封装为List<实体类对象>后,将该实体类转换为csv文件,然后上传到远程的sftp服务器指定目录的需求。 实现思路: List<实体类对象>转为csv文件的…...
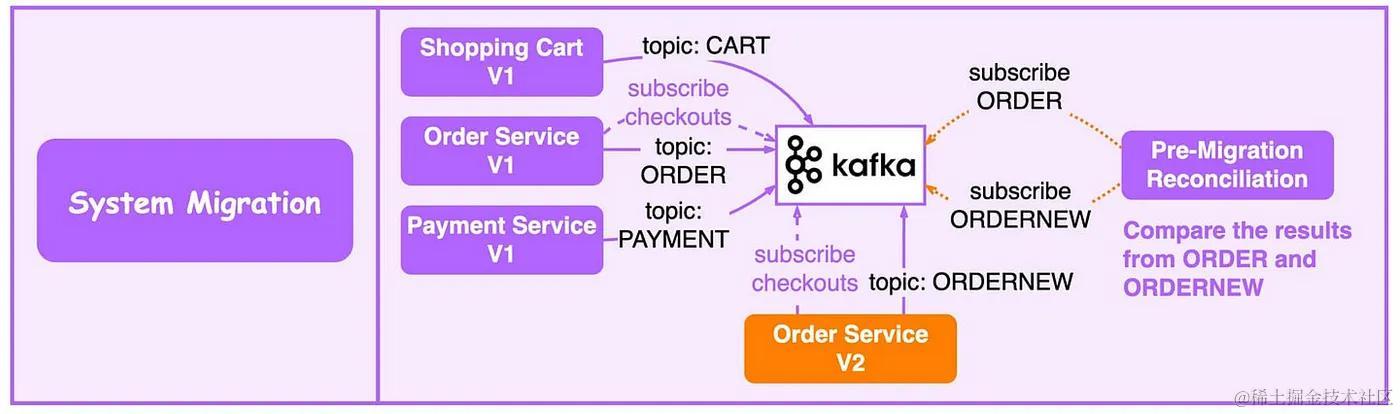
分享8个分布式Kafka的使用场景
Kafka 最初是为海量日志处理而构建的。它保留消息直到过期,并让消费者按照自己的节奏提取消息。与它的前辈不同,Kafka 不仅仅是一个消息队列,它还是一个适用于各种情况的开源事件流平台。 1. 日志处理与分析 下图显示了典型的 ELK࿰…...

【再见了暗恋对象 朋友们看完之后的一些感悟】
【再见了暗恋对象】写完之后魏野是我的第一个读者,魏野的反应是:这就是青春啊,喜欢了一个不喜欢自己的人而且男生觉得很困扰女孩子喜欢被牵引着走,但是男孩子牵引就是因为不喜欢这个女孩子,好可怜!青春就这…...

JSON和Protobuf序列化
文章目录 一、粘包和拆包1、半包问题2、半包现象原理 二、JSON协议通信1、通用类库2、JSON传输的编码器和解码器 三、Protobuf协议通信1、一个简单的proto文件的实践案例2、生成POJO和Builder3、消息POJO和Builder的使用案例1)构造POJO消息对象2)序列化和…...
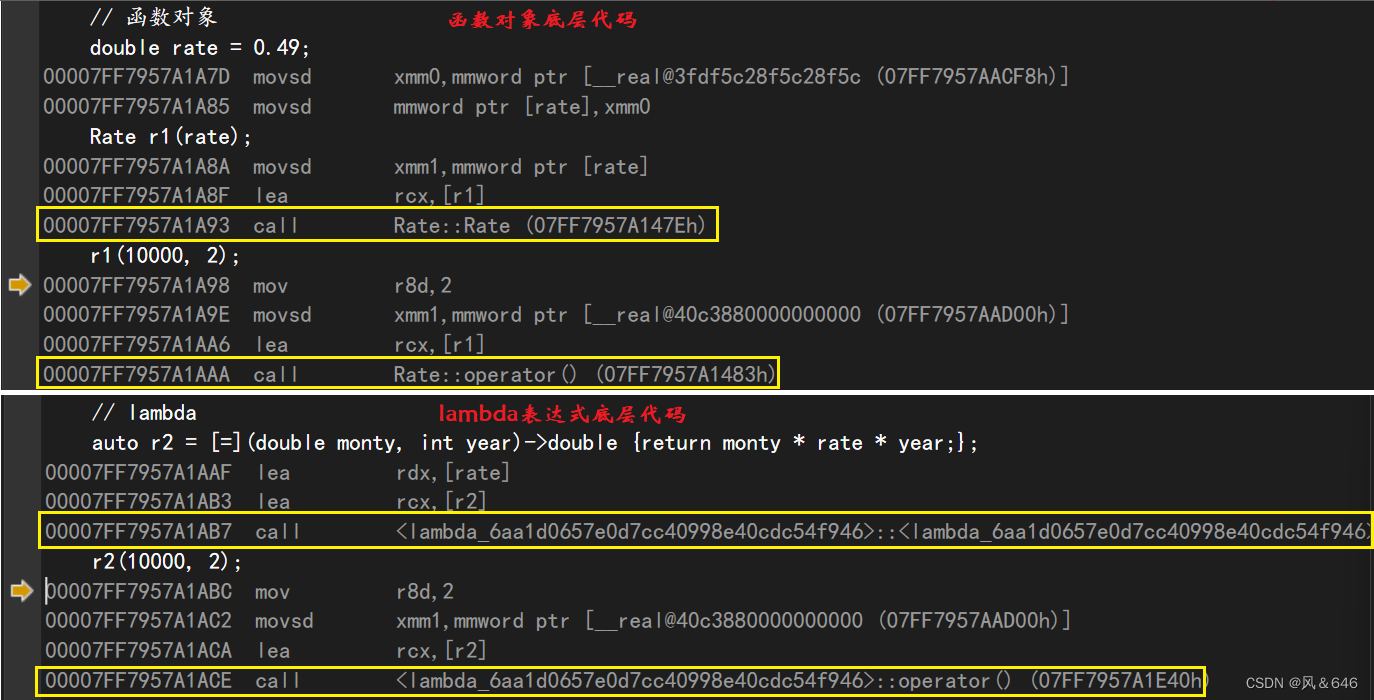
lambda表达式 - c++11
文章目录: lambda表达式概念lambda表达式语法函数对象与lambda表达式 lambda表达式概念 lambda 表达式是 c11 中引入的一种匿名函数,它可以在需要函数对象的地方使用,可以用作函数参数或返回值。lambda 表达式可以看作是一种局部定义的函数对…...

509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中 n > 1给定 n &a…...

四、[mysql]索引优化-1
目录 前言一、场景举例1.联合索引第一个字段用范围查询不走索引(分情况)2.强制走指定索引3.覆盖索引优化4.in和or在表数据量比较大的情况会走索引,在表记录不多的情况下会选择全表扫描5.like 后% 一般情况都会走索引(索引下推) 二、Mysql如何选择合适的索…...
:神经网络-最大池化使用)
PyTorch入门学习(九):神经网络-最大池化使用
目录 一、数据准备 二、创建神经网络模型 三、可视化最大池化效果 一、数据准备 首先,需要准备一个数据集来演示最大池化层的应用。在本例中,使用了CIFAR-10数据集,这是一个包含10个不同类别图像的数据集,用于分类任务。我们使…...
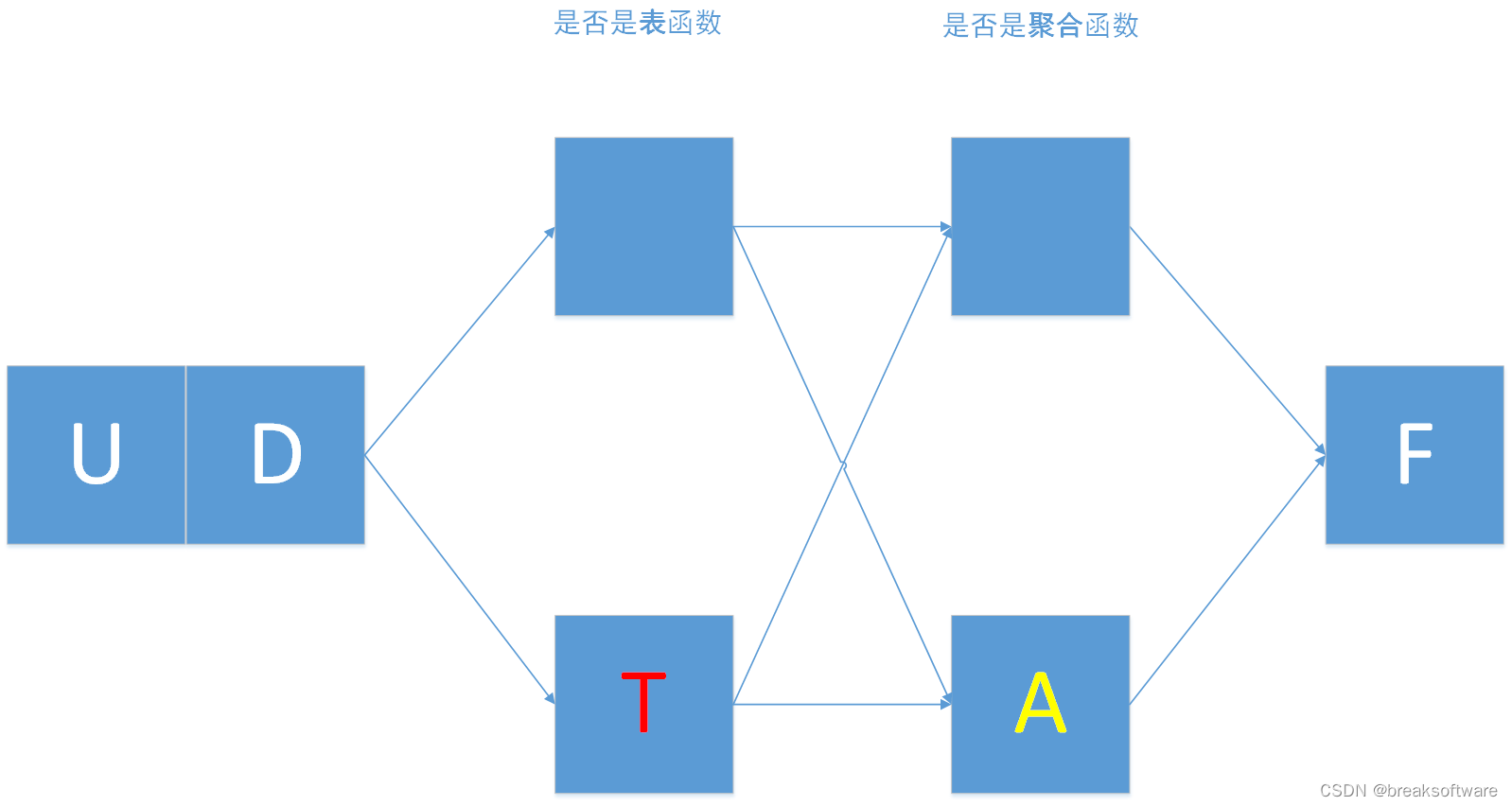
0基础学习PyFlink——用户自定义函数之UDF
大纲 标量函数入参并非表中一行(Row)入参是表中一行(Row)alias PyFlink中关于用户定义方法有: UDF:用户自定义函数。UDTF:用户自定义表值函数。UDAF:用户自定义聚合函数。UDTAF&…...

英语小作文模板(06求助+描述;07描述+建议)
06 求助描述: 题目背景及要求 第一段 第二段 第三段 翻译成中文 07 描述+建议: 题目背景及要求 第一段 第二段...

为什么感觉假期有时候比上班还累?
假期比上班还累的感觉可能由以下几个原因造成: 计划过度:在假期里,人们往往会制定各种计划,如旅游、聚会、休息等,以充分利用这段时间。然而,如果这些计划过于紧张或安排得过于紧密,就会导致身…...
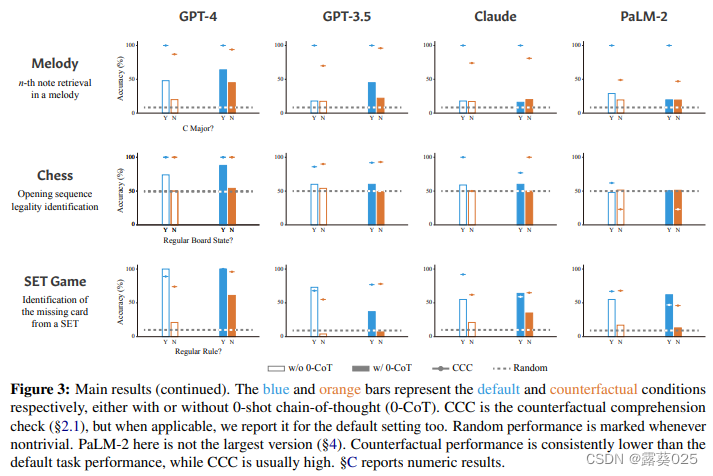
推理还是背诵?通过反事实任务探索语言模型的能力和局限性
推理还是背诵?通过反事实任务探索语言模型的能力和局限性 摘要1 引言2 反事实任务2.1 反事实理解检测 3 任务3.1 算术3.2 编程3.3 基本的句法推理3.4 带有一阶逻辑的自然语言推理3.5 空间推理3.6 绘图3.7 音乐3.8 国际象棋 4 结果5 分析5.1 反事实条件的“普遍性”5…...
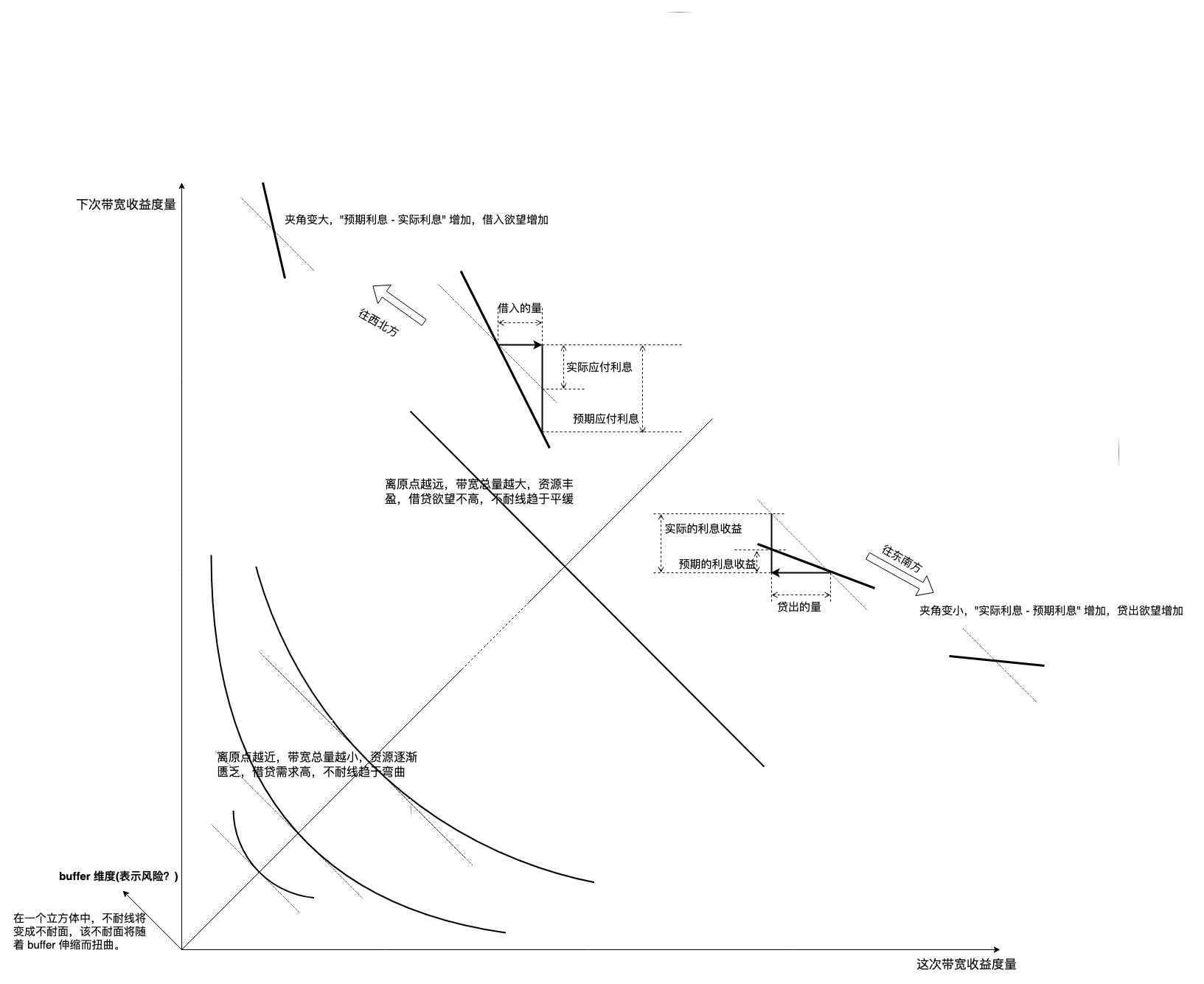
《利息理论》指导 TCP 拥塞控制
欧文费雪《利息原理》第 10 章,第 11 章对利息的几何说明是普适的,任何一个负反馈系统都能引申出新结论。给出原书图示,本文依据于此,详情参考原书: 将 burst 看作借贷是合理的,它包含成本(报文)…...
)
Bsdiff,Bspatch 的差分增量升级(基于Win和Linux)
目录 背景 内容 准备工作 在windows平台上 在linux平台上 正式工作 生成差分文件思路 作用差分文件思路 在保持相同目录结构进行差分增量升级 服务端(生成差分文件) 客户端(作用差分文件) 背景 像常见的Android 的linux平台,游戏,系统更新都…...

【3妹教我学历史-秦朝史】2 秦穆公-韩原之战
插: 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 坚持不懈,越努力越幸运,大家一起学习鸭~~~ 3妹:2哥,今天下班这么早&#…...

车载控制器
文章目录 车载控制器电动汽车上都有什么ECU 车载控制器 智能汽车上的控制器数量因车型和制造商而异。一般来说,现代汽车可能有50到100个电子控制单元(ECU)或控制器。这些控制器负责管理各种系统,如发动机管理、刹车、转向、空调、…...
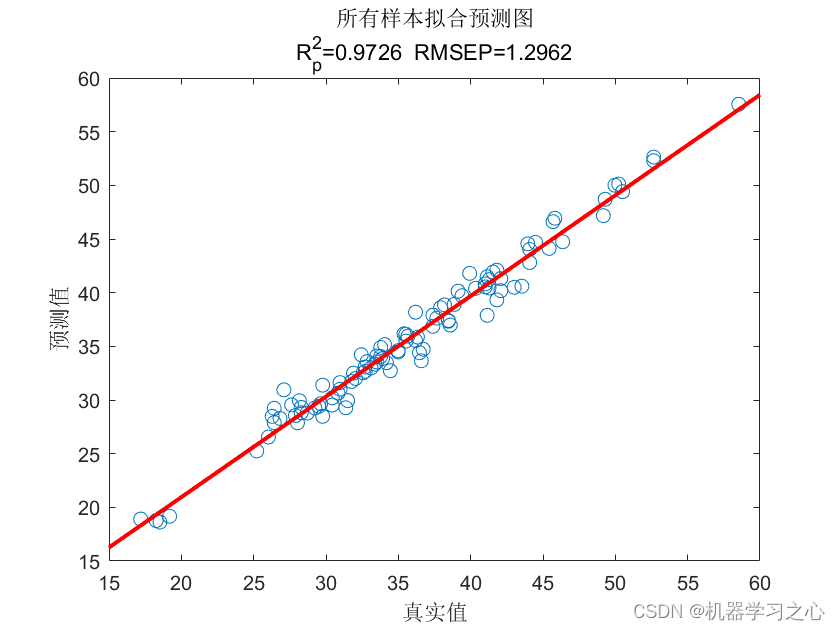
回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测
回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测 目录 回归预测 | Matlab实现RIME-CNN-SVM霜冰优化算法优化卷积神经网络-支持向量机的多变量回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.RIME-CNN-SVM霜冰优化算…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

Modbus转ETHERNET IP网关:快速冷却系统的智能化升级密钥
现代工业自动化系统中,无锡耐特森Modbus转Ethernet IP网关MCN-EN3001扮演着至关重要的角色。通过这一技术,传统的串行通讯协议Modbus得以在更高速、更稳定的以太网环境中运行,为快速冷却系统等关键设施的自动化控制提供了强有力的支撑。快速冷…...
