C/C++笔试易错与高频题型图解知识点(三)——数据结构部分(持续更新中)
目录
1. 排序
1.1 冒泡排序的改进
2. 二叉树
2.1 二叉树的性质
3. 栈 & 队列
3.1 循环队列
3.2 链式队列
4. 平衡二叉搜索树——AVL树、红黑树
5 优先级队列(堆)
1. 排序
1.1 冒泡排序的改进
下面的排序方法中,关键字比较次数与记录的初始排列无关的是______。
A. 希尔排序
B. 冒泡排序
C. 直接插入排序
D. 直接选择排序
答案:D
基础的冒泡排序是与初始排列无关的,但是改进的冒泡排序,当一趟排序之后没有交换,则说明序列已经有序,则可退出排序,例如一个已经排好序的序列,第一次循环之后就可以退出排序了;
所以说对比B选项和D选项,D选项肯定时最优解
2. 二叉树
2.1 二叉树的性质
① 对于任意一颗二叉树,设叶子节点个数为n0,度为二的节点的个数为n2,则满足n0 = n2 + 1
某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为() A. 不存在这样的二叉树
B. 200
C. 198(错误)
D. 199
答案:B
②深度
根节点的深度为0
③ 完全二叉树每一层的节点个数
一棵完全二叉树第六层有9个叶结点(根为第一层),则结点个数最多有()
A. 112
B. 111
C. 107
D. 109 (2^6-1 + 2^(7-1)-9*2 = 109)
答案:D :第六层满节点,题目要求第六层有9个叶子节点,则需要第六层的9个节点不挂叶子节点,所以第七层节点有2^(7-1)-9*2个节点
1. 满二叉树第i层节点个数:2^(i-1);
2. 总共i层的满二叉树所有节点个数:2^i - 1
3. 队列
3.1 循环队列
现有一循环队列,其队头指针为front,队尾指针为rear;循环队列长度为N。其队内有效长度为()(“左闭右开”)
A. (rear - front + N) % N + 1(错误)
B. (rear - front + N) % N
C. (rear - front) % (N + 1)
D. (rear - front + N) % (N - 1)
答案:B

3.2 链式队列
用不带头结点的单链表存储队列,其队头指针指向队头结点,队尾指针指向队尾结点,则在进行出队操作时()
A. 仅修改队头指针(错误)
B. 仅修改队尾指针
C. 队头、队尾指针都可能要修改
D. 队头、队尾指针都要修改
答案:C
※当队列只有一个节点时,出队列对头队尾指针均需要修改、
4. 栈
4.1 运算表达式
表达式3*2^(4+2*2-6*3)-5求值过程中当扫描到6时,对象栈和运算符栈为(),其中^为乘幂
A. 3,2,4,1,1;(*^(+*-
B. 3,2,8;(*^-(错误)
C. 3,2,4,2,2;(*^(-
D. 3,2,8;*^(-
答案:D
数据栈:有数据就直接入栈
运算符栈:设遍历到当前的运算符位x,如果栈不为空,比较栈顶与当前运算符优先级x,当栈顶运算符优先级大于或者等于x的优先级,则出栈,并将两个数据栈的数据出栈,计算出对应的数据,加入到数据栈中,否则将运算符入栈
/*根据上述原理模拟实现一个计算器*/
#include <iostream>
#include <unordered_map>
#include <stack>
#include <functional>
#include <string>#define MAX_PRI INT_MAXusing namespace std;
int main() {//数据栈stack<double> _data; //运算符栈stack<char> _operator; //运算符优先级unordered_map<char, int> pri{ {'+', 0}, {'-', 0}, {'*', 1}, {'/', 1}, {'^', 2}, {'(', MAX_PRI }, {')', MAX_PRI}};unordered_map<char, function<double(double, double)>> func{{'+', [](double x, double y) -> double { return x + y; }},{'-', [](double x, double y) -> double { return x - y; }}, {'*', [](double x, double y) -> double { return x * y; }},{'/', [](double x, double y) -> double { return x / y; }},{'^', [](double x, double y) -> double { return pow(x, y); }}};string exp;cin >> exp;auto calculate = [&_data, &_operator, &func]() {char op = _operator.top();_operator.pop();double x = _data.top();_data.pop();double y = _data.top();_data.pop();_data.push(func[op](y, x)); //运算顺序与出栈顺序相反};auto stringtonum = [&exp, &pri](int& i) -> double {int j = i + 1;while (j < exp.length() && pri.find(exp[j]) == pri.end()) j++;double num = stod(exp.substr(i, j - i));i = j - 1; return num;};for (int i = 0; i < exp.length(); ++i) {char e = exp[i];if (pri.find(e) == pri.end()) { //当前字符不是运算符,则切割数字_data.push(stringtonum(i));} else if (e == '(') {_operator.push('(');} else if (e == ')') {while (_operator.top() != '(') {calculate();}_operator.pop();} else {//当前运算符优先级<=栈顶运算符优先级,则出栈计算while (!_operator.empty() && pri[_operator.top()] >= pri[e] && _operator.top() != '(') {calculate();}_operator.push(e);}}while (!_operator.empty()) {calculate();}cout << _data.top() << endl;
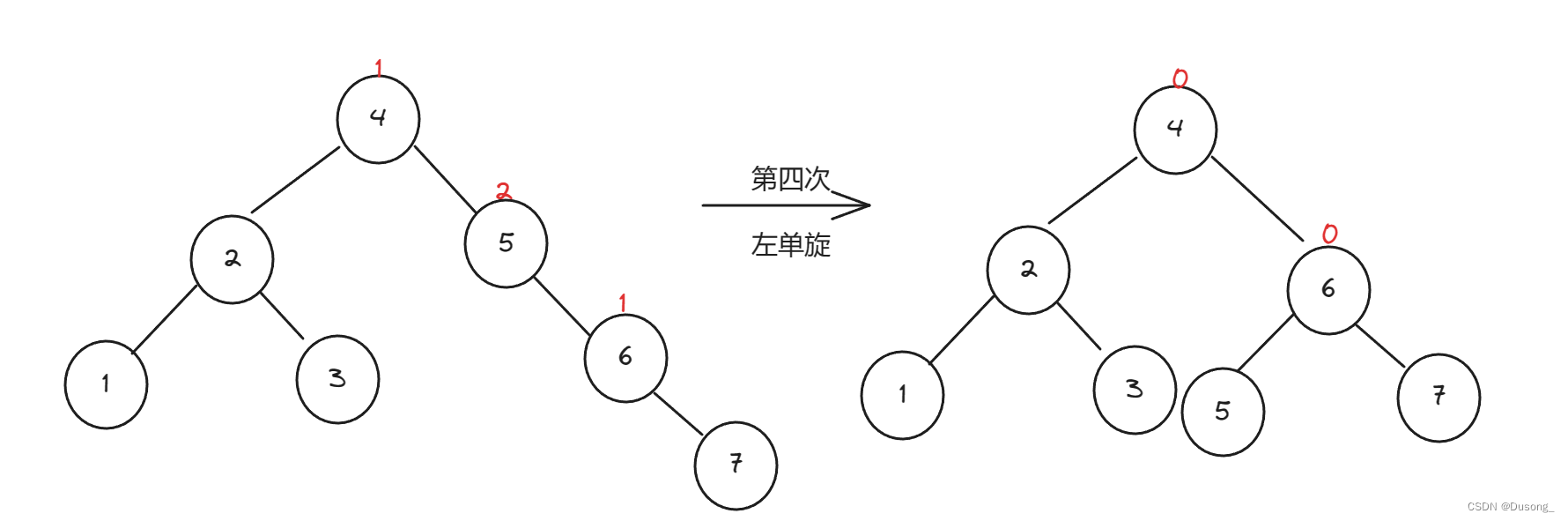
}5. 平衡二叉搜索树——AVL树、红黑树
若将关键字1,2,3,4,5,6,7 依次插入到初始为空的平衡二叉树 T 中,则 T 中平衡因子为 0 的分支结点的个数是( )
A. 0
B. 1
C. 2
D. 3
答案:D (分支节点:不包含叶子节点)



6. 优先级队列(堆)
下述二叉树中,哪一种满足性质:从任一结点出发到根的路径上所经过的结点序列按其关键字有序()
A. 二叉排序树(错误)
B. 哈夫曼树
C. AVL树
D. 堆
答案:D
知识点:小根堆与大根堆(详细看数据结构一、1.2节)
7. 哈希表
采用哈希表组织100万条记录,以支持字段A快速查找,则()
A. 理论上可以在常数时间内找到特定记录(错误:发生哈希冲突)
B. 所有记录必须存在内存中
C. 拉链式哈希曼最坏查找时间复杂度是O(n)
D. 哈希函数的选择跟A无关
答案:C
相关文章:

C/C++笔试易错与高频题型图解知识点(三)——数据结构部分(持续更新中)
目录 1. 排序 1.1 冒泡排序的改进 2. 二叉树 2.1 二叉树的性质 3. 栈 & 队列 3.1 循环队列 3.2 链式队列 4. 平衡二叉搜索树——AVL树、红黑树 5 优先级队列(堆) 1. 排序 1.1 冒泡排序的改进 下面的排序方法中,关键字比较次数与记录的初…...
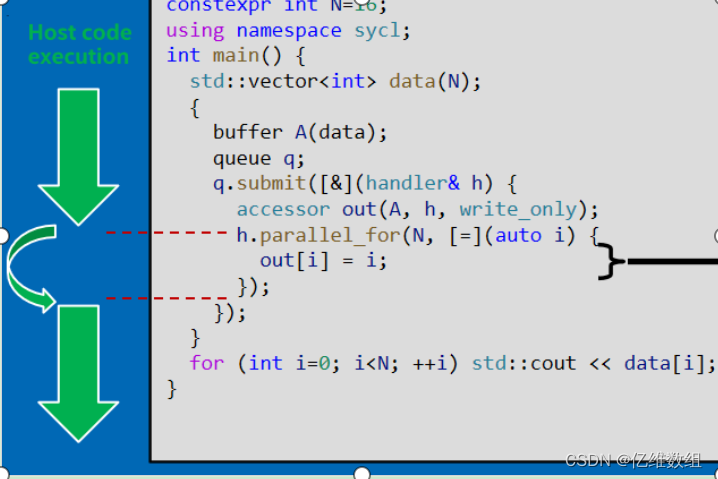
Intel oneAPI笔记--oneAPI简介、SYCL编程简介
oneAPI简介 Intel oneAPI是Intel提供的统一编程模型和软件开发框架。 它旨在简化可充分利用英特尔各种硬件架构(包括 CPU、GPU 和 FPGA)的应用程序的开发 oneAPI一个重要的特性是开放性,支持多种类型的架构和不同的硬件供应商,是…...
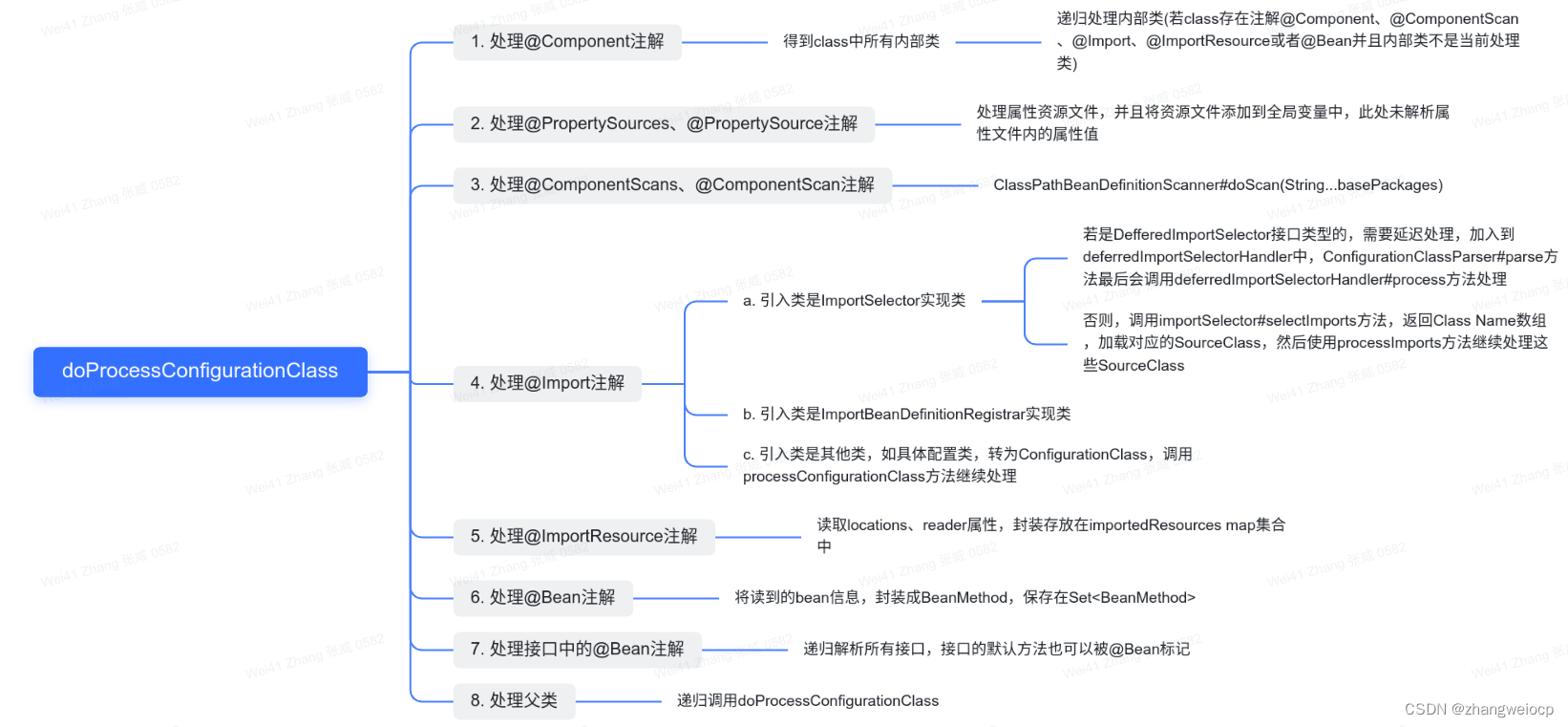
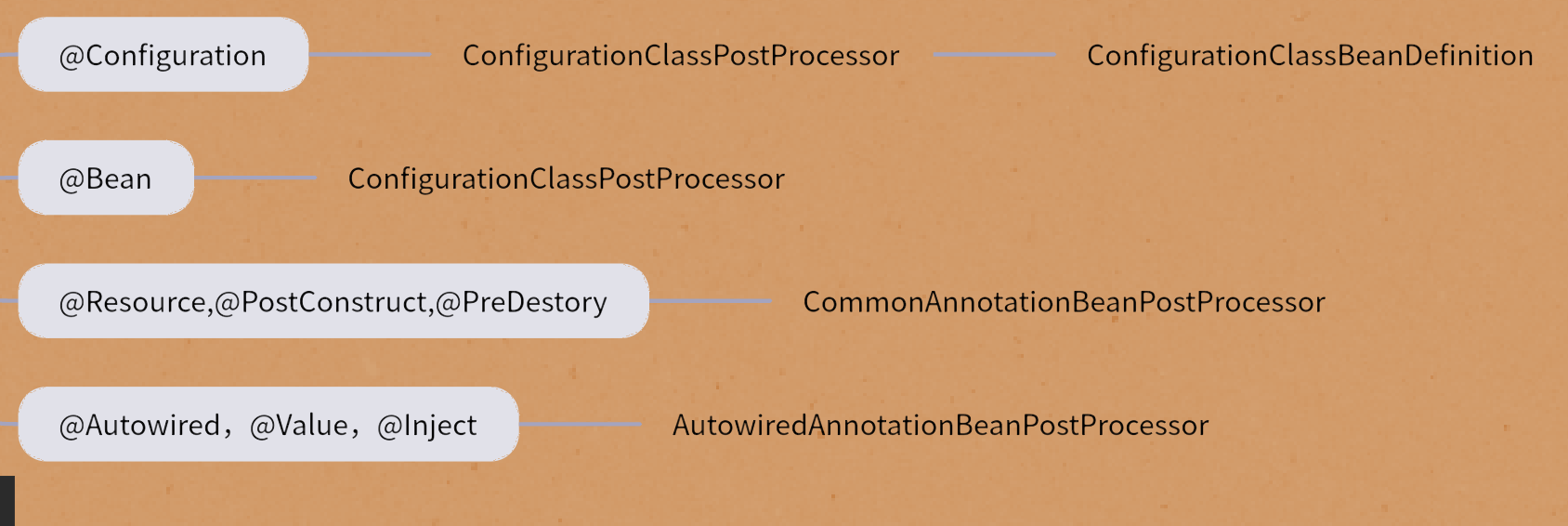
Spring IOC - ConfigurationClassPostProcessor源码解析
上文提到Spring在Bean扫描过程中,会手动将5个Processor类注册到beanDefinitionMap中,其中ConfigurationClassPostProcessor就是本文将要讲解的内容,该类会在refresh()方法中通过调用invokeBeanFactoryPosstProcessors(beanFactory)被调用。 5…...
Android OpenGL ES 2.0入门实践
本文既然是入门实践,就先从简单的2D图形开始,首先,参考两篇官方文档搭建个框架,便于写OpenGL ES相关的代码:构建 OpenGL ES 环境、OpenGL ES 2.0 及更高版本中的投影和相机视图。 先上代码,代码效果如下图…...

sql语句性能进阶必须了解的知识点——索引失效分析
在前面的文章中讲解了sql语句的优化策略 sql语句性能进阶必须了解的知识点——sql语句的优化方案-CSDN博客 sql语句的优化重点还有一处,那就是—— 索引!好多sql语句慢的本质原因就是设置的索引失效或者根本没有建立索引!今天我们就来总结一…...
ctfhub技能树web题目全解
Rce 文件包含 靶场环境 重点是这个代码,strpos,格式是这样的strpoc(1,2,3) 1是要搜索的字符串,必须有;2是要查询的字符串,必须有;3是在何处开始查询&#…...

AMD、CMD、UMD是什么?
AMD(Asynchronous Module Definition)、CMD(Common Module Definition)和UMD(Universal Module Definition)是JavaScript模块化规范,用于管理和组织JavaScript代码的模块化加载和依赖管理。 1:AMD(异步模块定义): AMD是由RequireJS提出的模块化规范。它支持异步加载…...

AM@微分方程相关概念@线性微分方程@一阶线性微分方程的通解
文章目录 abstract引言 一般的微分方程常微分方程微分方程的解隐式解通解和特解初始条件初值问题微分方程的积分曲线 线性微分方程一阶线性微分方程一阶齐次和非齐次线性微分方程一阶齐次线性微分方程的解一阶非齐次线性微分方程的解 abstract AM微分方程相关概念线性微分方程…...

基于深度学习的安全帽识别检测系统(python OpenCV yolov5)
收藏和点赞,您的关注是我创作的动力 文章目录 概要 一、研究的内容与方法二、基于深度学习的安全帽识别算法2.1 深度学习2.2 算法流程2.3 目标检测算法2.3.1 Faster R-CNN2.3.2 SSD2.3.3 YOLO v3 三 实验与结果分析3.1 实验数据集3.1.1 实验数据集的构建3.1.2 数据…...
Spring源码分析篇一 @Autowired 是怎样完成注入的?究竟是byType还是byName亦两者皆有
1. 五种不同场景下 Autowired 的使用 第一种情况 上下文中只有一个同类型的bean 配置类 package org.example.bean;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration;Configuration public class FruitCo…...

Goby 漏洞发布|F5 BIG-IP AJP 身份认证绕过漏洞(CVE-2023-46747)
漏洞名称:F5 BIG-IP AJP 身份认证绕过漏洞(CVE-2023-46747) English Name:F5 BIG-IP AJP authentication bypass vulnerability (CVE-2023-46747) CVSS core: 10 影响资产数: 307282 漏洞描述: Cisco …...

Vue中watch侦听器用法
watch 需要侦听特定的数据源,并在单独的回调函数中执行副作用 watch第一个参数监听源 watch第二个参数回调函数cb(newVal,oldVal) watch第三个参数一个options配置项是一个对象{ immediate:true //是否立即调用一次 deep:true //是否开启…...

[算法前沿]--054-大语言模型的学习材料
大语言模型的学习材料 Other Papers If you’re interested in the field of LLM, you may find the above list of milestone papers helpful to explore its history and state-of-the-art. However, each direction of LLM offers a unique set of insights and contribut…...

DWA算法,仿真转为C用于无人机避障
DWA算法,仿真转为C用于无人机避障 链接: 机器人局部避障的动态窗口法(dynamic window approach) 链接: 机器人局部避障的动态窗口法DWA (dynamic window approach)仿真源码详细注释版 链接: 常见路径规划算法代码-Matlab (纯代码篇) …...

现阶段的主流数据库分别是哪几种?
关系型数据库 1. MySQL数据库 MySQL是最受欢迎的开源SQL数据库管理系统,它由 MySQL AB开发、发布和支持。MySQL AB是一家基于MySQL开发人员的商业公司,它是一家使用了一种成功的商业模式来结合开源价值和方法论的第二代开源公司。MySQL是MySQL AB的注册商…...
“原生感”暴涨311%,这届年轻人不再爱浓妆?丨小红书数据分析
近年来,越来越多美妆博主在社交媒体平台安利“原生感妆容”,即我们所熟知的“伪素颜妆”、“裸妆”、“白开水妆”,显然,追求“原生感”成为当代妆容主流。通过小红书数据分析工具,查看#原生感妆容 话题,近…...
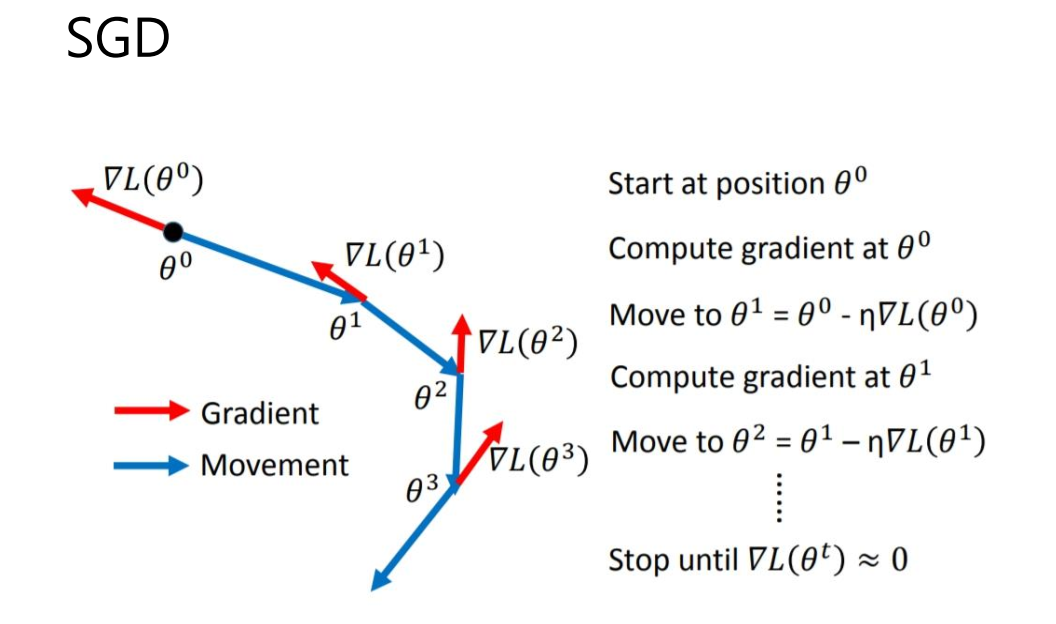
基于深度学习的植物识别算法 - cnn opencv python 计算机竞赛
文章目录 0 前言1 课题背景2 具体实现3 数据收集和处理3 MobileNetV2网络4 损失函数softmax 交叉熵4.1 softmax函数4.2 交叉熵损失函数 5 优化器SGD6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习的植物识别算法 ** …...
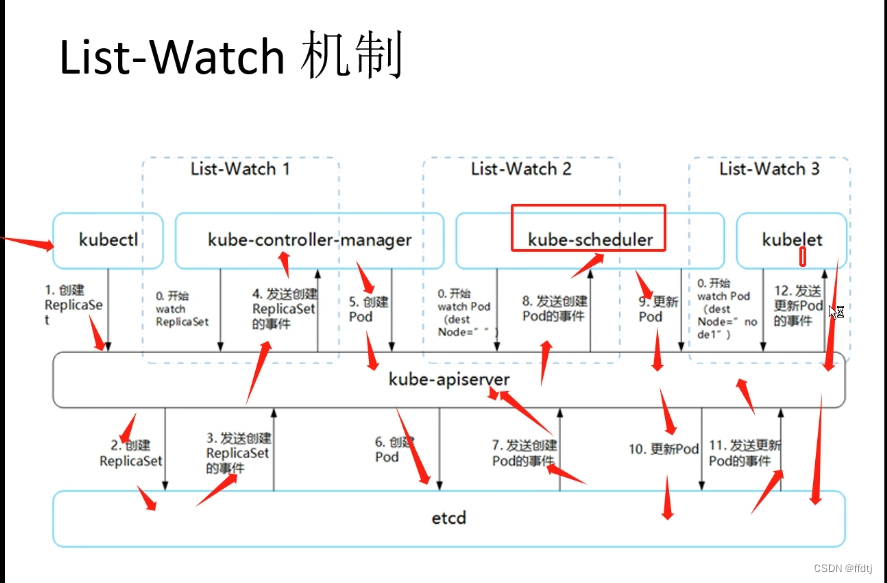
k8s调度约束
List-Watch Kubernetes 是通过 List-Watch的机制进行每个组件的协作,保持数据同步的,每个组件之间的设计实现了解耦。 List-Watch机制 工作机制:用户通过 kubectl请求给 APIServer 来建立一个 Pod。APIServer会将Pod相关元信息存入 etcd 中…...
面经(面试经验)第一步,从自我介绍开始说起
看到一位同学讲自己的面试步骤和过程,我心有所感,故此想整理下面试的准备工作。以便大家能顺利应对面试,通过面试... 求职应聘找工作,面试是必然的关卡,如今竞争激烈呀,想要得到自己喜欢的工作,…...
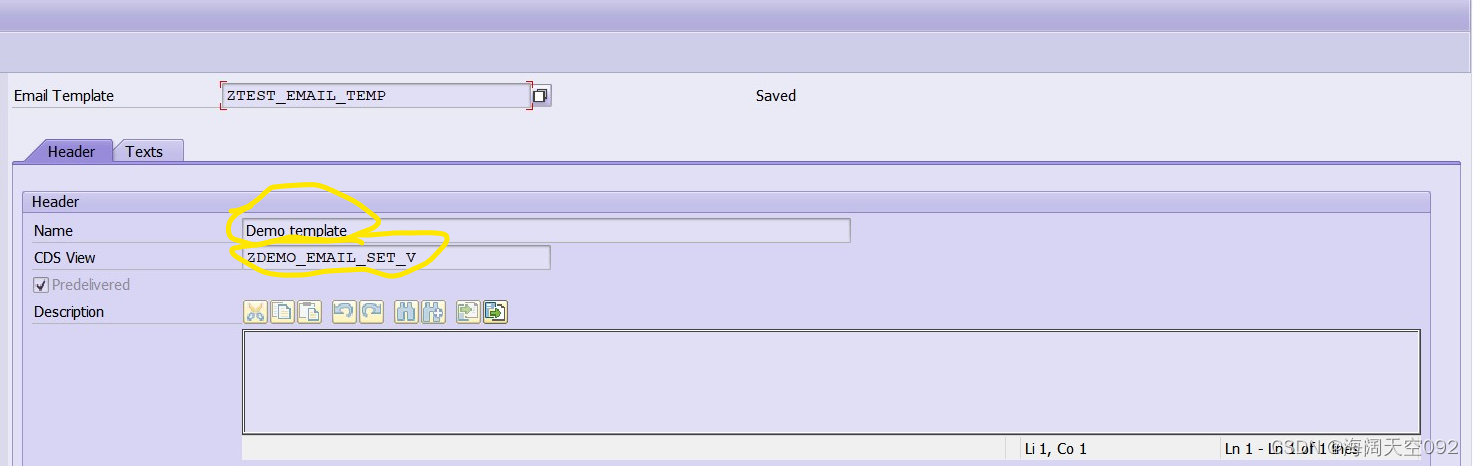
S/4 HANA 中的 Email Template
1 如何创建Email Template? 没有特定的事务用于创建电子邮件模板,我们可以将其创建为 SE80 事务中的存储库对象,如下所示: 1,选择包(或本地对象)并右键单击。 2,选择“创建”->“更多”->“电子邮件模板” 尽管如此,对于已有的Email Template,可以使用程序…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
