关键路径及关键路径算法[C/C++]
文章目录
- 关键路径
- 引例
- AOE网
- 关键路径与关键活动
- 关键路径算法
- 引例与原理
- 关键路径算法的实现
- 边的存储结构
- 代码实现
- 运行示例
关键路径
关于拓扑排序的内容见拓扑排序详解
引例
通过拓扑排序我们可以解决一个工程是否可以顺序进行的问题,拓扑排序把一个工程分成了若干个流水级,只有当前流水级的工作完成才能进入下一个流水级,然而有时候我们还要解决工程完成的最短时间问题。比如说,造一辆汽车,我们要先造各种各样的零件、部件,最终再组装成车。
这些零部件都是在流水线上同时生产的,假如造一个轮子需要0.5天,造一个发动机需要3天,造一个车底盘需要2天,造一个外壳需要2天,造其他零部件需要2天,全部零部件集中到一处需要0.5天,组装成车需要2天,那么我们生产一辆车最短需要几天呢?
如果回答说把所有时间加起来,假如所有活动是串行的话,那么自然是每个活动时间相加,但是这些零件是分别在流水线上同时生产的,也就是说生产发动机的3天内我们可能已经生产了6个轮子,1.5个外壳,1.5个底盘了,而车的组装是在所有零部件都生产好之后才可以进行的,因此最短时间应该是先导活动中时间最长的发动机3天+集中零部件0.5天+组装车的2天,一共5.5天完成一辆车的生产。
因此,我们如果要对一个流程图求最短完成时间,就要分析它们的拓扑关系,并找到其中的关键流程,这个流程的时间就是最短时间。
AOE网
基于我们拓扑排序中AOV网(Activity On Vertex Network),我们根据求流程的最短时间的需求,提出一个新的概念。在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,边上的权值表示活动的持续时间,这种有向图的边表示活动的网,我们称之为AOE网(Activity On Edge Network).
我们把AOE网中入度为0的点称为始点或源点,出度为0的点称为终点或汇点,它们分别代表工程的开始和结束,所以正常情况下,AOE网只有一个源点和一个汇点。如下图中,顶点vi代表一个事件,弧<vi , vj>则表示一个活动,其权值代表活动的持续时间。
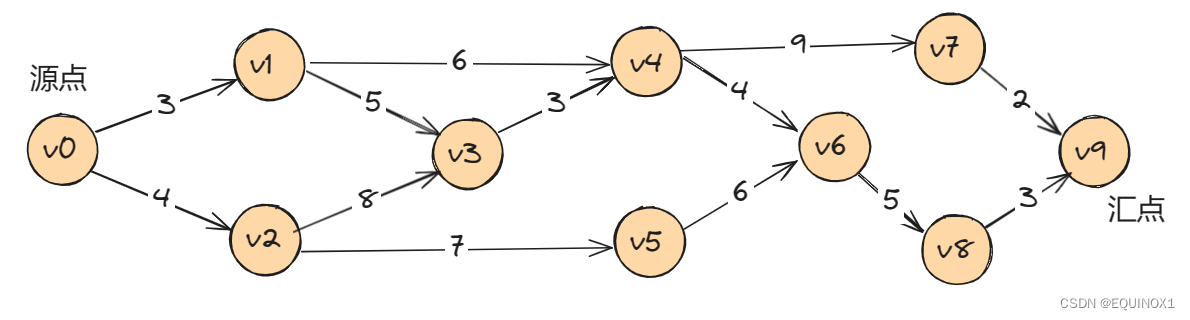
AOE网有着明显的工程特性,只有某顶点的事件发生后,由该顶点出发的各项活动才能开始。只有进入该顶点的所有活动都已经结束,该顶点的事件才能发生。
AOE网和AOV网有着相似之处,二者都是对工程进行建模,但又有很大差别。AOV网用顶点表示活动,它描述了活动间的偏序关系,AOE网则用边来表示活动,边上的权值表示活动的持续时间。仍以我们汽车的流水线生产为例,其AOV网和AOE网的对比体现了二者的差别。AOE网是建立在活动的偏序关系(或制约关系)没有矛盾的基础上,再来分析整个工程至少需要多少时间,以及为了缩短工程时间,可以加快哪些活动,或者对于各个活动ddl的限制等。

关键路径与关键活动
我们把路径上各个活动所持续的时间之和称为路径长度,从源点到汇点具有最大长度的路径叫关键路径,在关键路径上的活动叫关键活动。显然就上图的AOE网而言,开始→发动机完成→部件集中到位→组装完成就是关键路径,路径长度为5.5。
我们发现,如果我们加快非关键路径上的活动,并不会缩短整个工程的时间,即使一个轮子只需要0.1的生产时间也无济于事,但是如果我们缩短了关键路径上关键活动的时间,如发动机缩短为2.5天,组装车缩短为1.5天,那么我们的关键路径长度就缩短为了4.5天。
所以我们如何去求关键路径呢?
关键路径算法
引例与原理
这是关于关键路径的一个很经典的例子。假设一个学生放学回家,除掉吃饭、洗漱外,到睡觉前有四小时空闲,而家庭作业需要两小时完成。不同的学生会有不同的做法,抓紧的学生,会在头两小时就完成作业,然后看看电视、读读课外书什么的;但也有超过一半的学生(比如我(悲))会在最后两小时才去做作业,要不是因为没时间,可能还要再拖延下去。这也没什么好奇怪的,拖延就是人性几大弱点之一。
这里做家庭作业这一活动的最早开始时间是四小时的开始,可以理解为0,而最晚开始时间是两小时之后马上开始,不可以再晚,否则就是延迟了,此时可以理解为2。显然,当最早和最晚开始时间不相等时就意味着有空闲。接着,老妈发现了孩子拖延的小秘密(太痛了x_x),于是买了很多的课外习题,要求你四个小时,不许有一丝空闲,省得你拖延或偷懒。此时整个四小时全部被占满,最早开始时间和最晚开始时间都是0,因此它就是关键活动了。也就是说,我们只需要找到所有活动的最早开始时间和最晚开始时间,并且比较它们,如果相等就意味着此活动是关键活动,活动间的路径为关键路径。如果不等,则就不是。
关键路径算法的实现
那么关键路径的求解过程如下:
-
用数组etv(earliest time of vertex)和ltv(latest time of vertex)来存储事件的最早/最晚发生时间
-
e t v [ k ] = { 0 , 当 k = 0 时 m a x { e t v [ i ] + l e n < v i , v k > } . , 当 k ≠ 0 且 < v i , v k > ∈ p [ k ] 时 etv[k] = \left\{\begin{matrix} 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,当k=0时\\ max\left \{ etv[i]+len<vi,vk>\right \} .,当k≠0且 <vi,vk>∈p[k]时 \end{matrix}\right. etv[k]={0 ,当k=0时max{etv[i]+len<vi,vk>}.,当k=0且<vi,vk>∈p[k]时
其中p[ k ]为所有到达vk的边集合,转移方程保证了事件k在etv[ k ]发生时,其所有先导活动都能完成
-
l t v [ k ] = { e t v [ k ] , 当 k = n − 1 时 m i n { l t v [ j ] − l e n < v k , v j > } , 当 k ≠ n − 1 且 < v k , v j > ∈ S [ k ] 时 ltv[k] = \left\{\begin{matrix} etv[k]\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,当k=n-1时\\ min\left \{ ltv[j]-len<vk,vj>\right \} ,当k≠n-1且 <vk,vj>∈S[k]时 \end{matrix}\right. ltv[k]={etv[k] ,当k=n−1时min{ltv[j]−len<vk,vj>},当k=n−1且<vk,vj>∈S[k]时
其中S[k]为vk发出的边集合,转移方程保证了事件k在ltv[ k ]发生时,其发出的所有活动到达的事件都能在其最早开始时间完成
-
活动的最早开始时间即其先导事件的最早发生时间,因此只有先导事件发生了,活动才能开始
-
活动的最晚开始时间是其抵达事件的最晚发生时间减去活动时长,活动再晚也不能等其到达的事件发生了才开始,所以要赶在到达的事件发生之前
这里我们使用邻接表来存储边。
边的存储结构
vector<int> etv, ltv; // 事件最早发生时间
stack<int> path; // 存储拓扑序列
struct Edge
{Edge(int a, int w) : adjvex(a), weight(w), _next(nullptr){}// int in;//边的起点,这里省去int adjvex;//边的终点int weight;//权值Edge *_next;//in发出的下一条边
};
代码实现
求解etv的过程就是一次拓扑排序,只不过加了行对于elv的更新,开始事件的etv显然是0,由开始事件往后由拓扑顺序更新etv
而求解ltv其实就是对于拓扑排序的逆过程,因为结束事件的etv和ltv显然相同,那么对拓扑序列逆向遍历,更新ltv
再根据ltv,etv和lte,ete的关系求寻找我们的关键活动
void TopoLogicalSort(vector<Edge *> &edges)
{int n = edges.size();etv.resize(n);vector<int> ind(n); // 记录入度for (auto e : edges){while (e){ind[e->adjvex]++;e = e->_next;}}queue<int> q;for (int i = 0; i < n; i++)if (!ind[i])q.push(i);int f;while (!q.empty()){f = q.front();q.pop();path.push(f); // 存储拓扑序列Edge *e = edges[f];while (e){if (!(--ind[e->adjvex]))q.push(e->adjvex);if (e->weight + etv[f] > etv[e->adjvex])// 如果事件f的etv + 活动e的时间晚于etv[adjvex],则更新事件adjvex的etv,保证adjvex的etv时,事件adjvex的所有先导活动都已完成etv[e->adjvex] = e->weight + etv[f];e = e->_next;}}
}
void CriticalPath(vector<Edge *> &edges)
{Edge *e = nullptr;int ete, lte; // 活动的最早最晚发生时间int n = edges.size(), t;TopoLogicalSort(edges);ltv.resize(n);for (int i = 0; i < n; i++)ltv[i] = etv[n - 1]; // 初始化最晚发生时间while (!path.empty()){t = path.top();path.pop();e = edges[t];while (e){if (etv[e->adjvex] - e->weight < ltv[t]) // 保证事件t如果在etv开始,发出的活动到达的事件都能在其各自etv完成ltv[t] = etv[e->adjvex] - e->weight;e = e->_next;}}for (int i = 0; i < n; i++){e = edges[i];ete = etv[i]; // 事件的最早发生时间和其发出活动的最早发生时间一致while (e){lte = ltv[e->adjvex] - e->weight;if (lte == ete){printf("<v%d-v%d> length:%d\n", i, e->adjvex, e->weight);break;}e = e->_next;}}
}
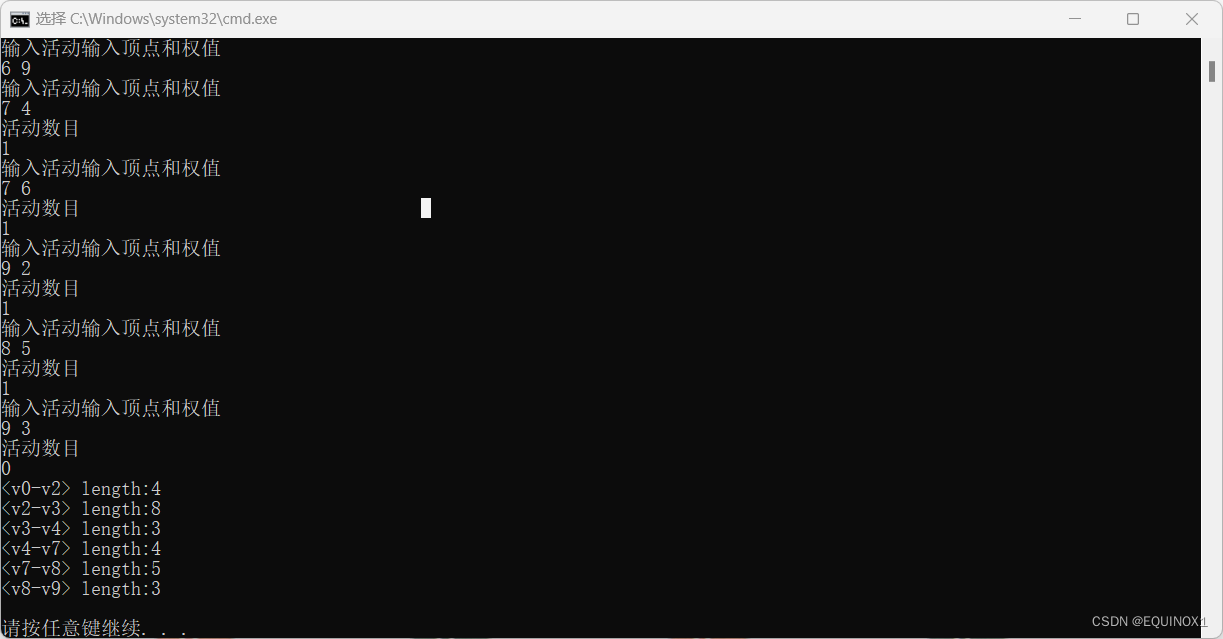
运行示例
运行代码
#include <iostream>
#include <vector>
#include <queue>
#include <stack>
using namespace std;
vector<int> etv, ltv; // 事件最早发生时间
stack<int> path; // 存储拓扑序列
struct Edge
{Edge(int a, int w) : adjvex(a), weight(w), _next(nullptr){}// int in;int adjvex;int weight;Edge *_next;
};
void TopoLogicalSort(vector<Edge *> &edges)
{int n = edges.size();etv.resize(n);vector<int> ind(n); // 记录入度for (auto e : edges){while (e){ind[e->adjvex]++;e = e->_next;}}queue<int> q;for (int i = 0; i < n; i++)if (!ind[i])q.push(i);int f;while (!q.empty()){f = q.front();q.pop();path.push(f); // 存储拓扑序列Edge *e = edges[f];while (e){if (!(--ind[e->adjvex]))q.push(e->adjvex);if (e->weight + etv[f] > etv[e->adjvex])// 如果事件f的etv + 活动e的时间晚于etv[adjvex],则更新事件adjvex的etv,保证adjvex的etv时,事件adjvex的所有先导活动都已完成etv[e->adjvex] = e->weight + etv[f];e = e->_next;}}
}
void CriticalPath(vector<Edge *> &edges)
{Edge *e = nullptr;int ete, lte; // 活动的最早最晚发生时间int n = edges.size(), t;TopoLogicalSort(edges);ltv.resize(n);for (int i = 0; i < n; i++)ltv[i] = etv[n - 1]; // 初始化最晚发生时间while (!path.empty()){t = path.top();path.pop();e = edges[t];while (e){if (etv[e->adjvex] - e->weight < ltv[t]) // 保证事件t如果在etv开始,发出的活动到达的事件都能在其各自etv完成ltv[t] = etv[e->adjvex] - e->weight;e = e->_next;}}for (int i = 0; i < n; i++){e = edges[i];ete = etv[i]; // 事件的最早发生时间和其发出活动的最早发生时间一致while (e){lte = ltv[e->adjvex] - e->weight;if (lte == ete){printf("<v%d-v%d> length:%d\n", i, e->adjvex, e->weight);break;}e = e->_next;}}
}
int main()
{int n, cnt, adj, w;cout << "请输入事件数量" << endl;cin >> n;Edge *e;vector<Edge *> edges(n, nullptr);for (int i = 0; i < n; i++){cout << "活动数目" << endl;cin >> cnt;for (int j = 0; j < cnt; j++){cout << "输入活动输入顶点和权值" << endl;cin >> adj >> w;e = new Edge(adj, w);e->_next = edges[i];edges[i] = e;}}CriticalPath(edges);return 0;
}
相关文章:

关键路径及关键路径算法[C/C++]
文章目录 关键路径引例AOE网关键路径与关键活动关键路径算法引例与原理关键路径算法的实现边的存储结构代码实现运行示例 关键路径 关于拓扑排序的内容见拓扑排序详解 引例 通过拓扑排序我们可以解决一个工程是否可以顺序进行的问题,拓扑排序把一个工程分成了若干…...

nginx http 跳转到https
改 Nginx 配置文件 在您安装了 SSL 证书之后,您需要修改 Nginx 的配置文件以启用 HTTPS 和 HTTP 自动跳转 HTTPS。 打开 Nginx 配置文件(通常位于 /etc/nginx/nginx.conf),找到您的网站配置块。在该配置块中添加以下内容&#x…...

可靠的互联网兼职平台,平常可以做副业充实生活
在互联网时代,越来越多的人开始通过网络来寻找兼职副业的机会,能够更灵活地安排自己的时间,实现自己的收入增值。那么找到一个正规可靠的线上兼职平台就是一个比较重要的事情,这里分享几个正规靠谱的线上兼职副业平台,…...
云安全—K8s APi Server 6443 攻击面
0x00 前言 在未授权的一文中,详细描述了k8s api中的8080端口未授权的问题,那么本篇主要来说6443端口的利用。 0x01 API连接攻击面 1.匿名用户访问 匿名开放方式:kubectl create clusterrolebinding cluster-system-anonymous --clusterro…...

【案例实战】NodeJS+Vue3+MySQL实现列表查询功能
这篇文章,给大家带来一个列表查询的功能,从前端到后端的一个综合案例实战。 采用vue3作为前端开发,nodejs作为后端开发。 首先我们先来看一下完成的页面效果。点击分页,可以切换到上一页、下一页。搜索框可以进行模糊查询。 后端…...
Google play开发者账号被封的几种常见原因及相关解决思路
在Google paly上,每天都有大量的应用被成功发布,同时也有很多开发者账号被封禁。特别是在今年的十月份之前,谷歌的"封号潮"给很多开发者带来了沉重的打击。不过,令人欣慰的是,自十月份之后,情况逐…...

深入理解计算机系统CS213学习笔记
Lecture 01 1. 计算机表示数字 int 整数运算可能会出现错误,超过32位时会出现溢出。 float 浮点数不适用结合律,因为浮点数表示的精度有限。 根其原因,是用有限的位数表示无限的数字空间。 2.利用分层的存储系统,使程序运行更…...
【设计模式】第8节:结构型模式之“适配器模式”
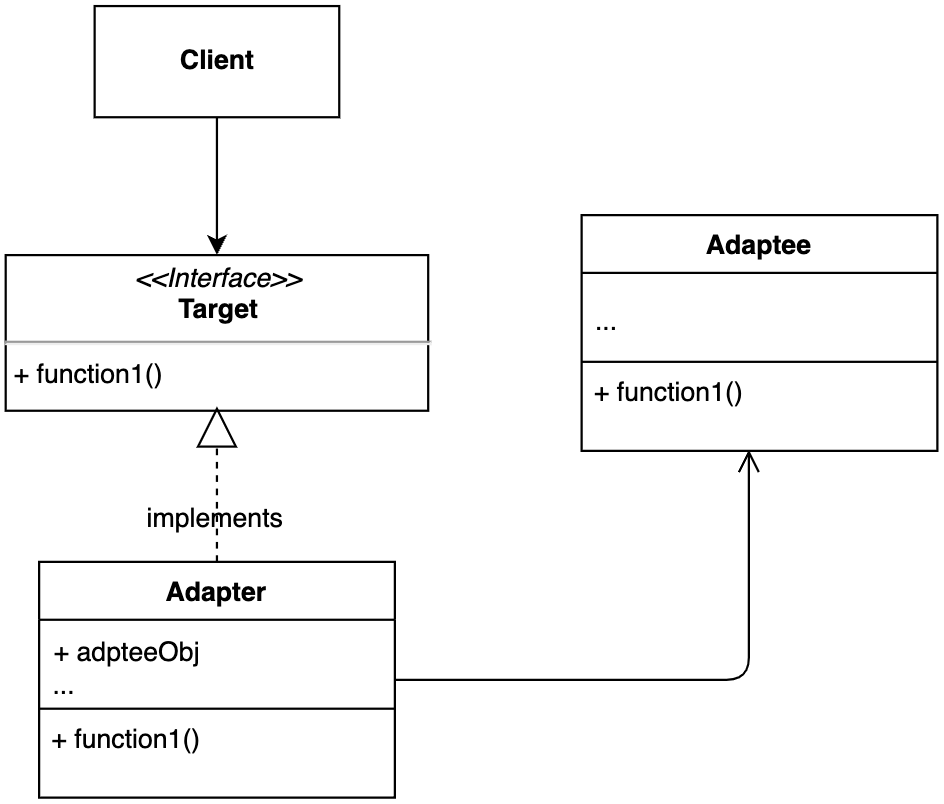
一、简介 适配器模式是用来做适配的,它将不兼容的接口转换为可兼容的接口,让原本由于接口不兼容而不能一起工作的类可以一起工作。 适配器模式角色: 请求者client:调用服务的角色目标Target:定义了Client要使用的功…...
Stable Diffusion WebUI扩展openpose-editor如何使用
先上地址: GitHub - fkunn1326/openpose-editor: Openpose Editor for AUTOMATIC1111s stable-diffusion-webuiOpenpose Editor for AUTOMATIC1111s stable-diffusion-webui - GitHub - fkunn1326/openpose-editor: Openpose Editor for AUTOMATIC1111s stable-diffusion-webu…...

企业网络带宽使用情况检查技巧
想要提高网络性能的企业通常会考虑限制对占用带宽的应用程序(如社交媒体和视频流应用程序)的访问,但对于那些真正需要获得高效网络的人来说,这还不够,您需要定期跟踪带宽使用情况。 虽然有许多工具可以帮助您检查网络…...
C/C++笔试易错与高频题型图解知识点(三)——数据结构部分(持续更新中)
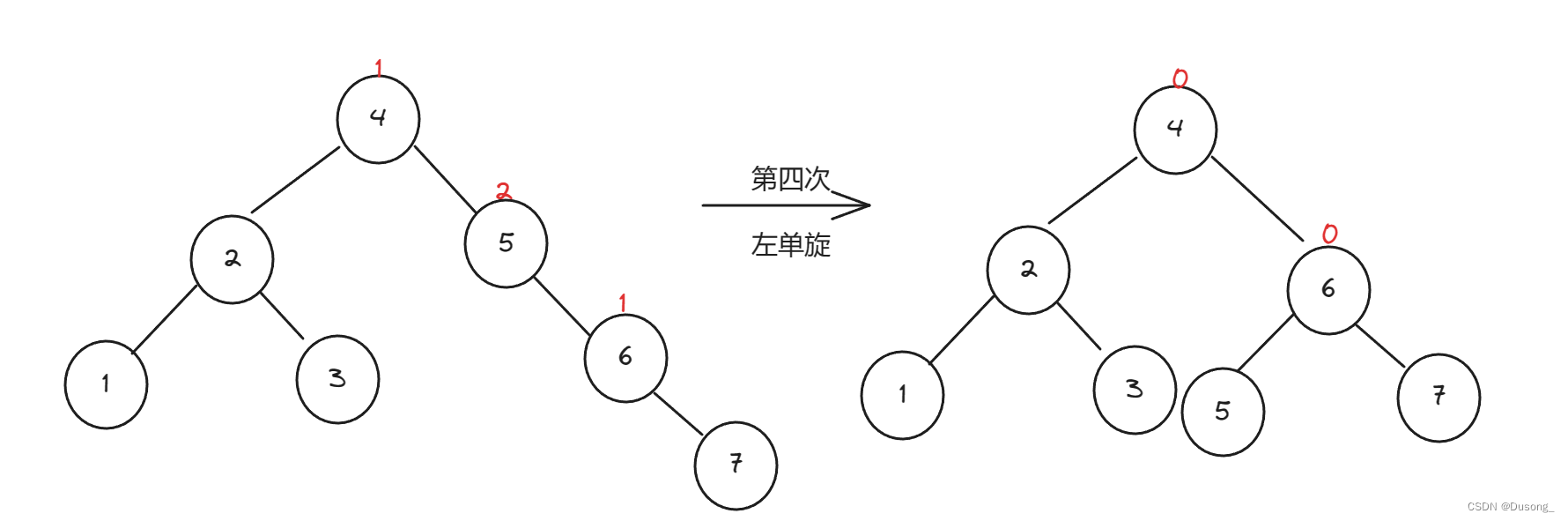
目录 1. 排序 1.1 冒泡排序的改进 2. 二叉树 2.1 二叉树的性质 3. 栈 & 队列 3.1 循环队列 3.2 链式队列 4. 平衡二叉搜索树——AVL树、红黑树 5 优先级队列(堆) 1. 排序 1.1 冒泡排序的改进 下面的排序方法中,关键字比较次数与记录的初…...
Intel oneAPI笔记--oneAPI简介、SYCL编程简介
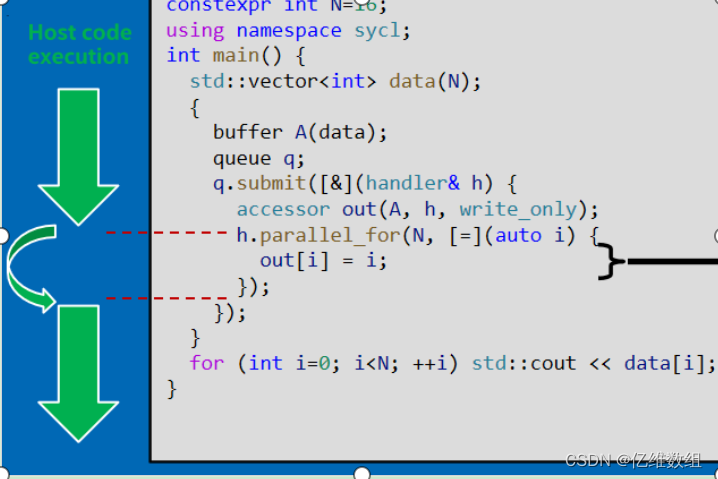
oneAPI简介 Intel oneAPI是Intel提供的统一编程模型和软件开发框架。 它旨在简化可充分利用英特尔各种硬件架构(包括 CPU、GPU 和 FPGA)的应用程序的开发 oneAPI一个重要的特性是开放性,支持多种类型的架构和不同的硬件供应商,是…...
Spring IOC - ConfigurationClassPostProcessor源码解析
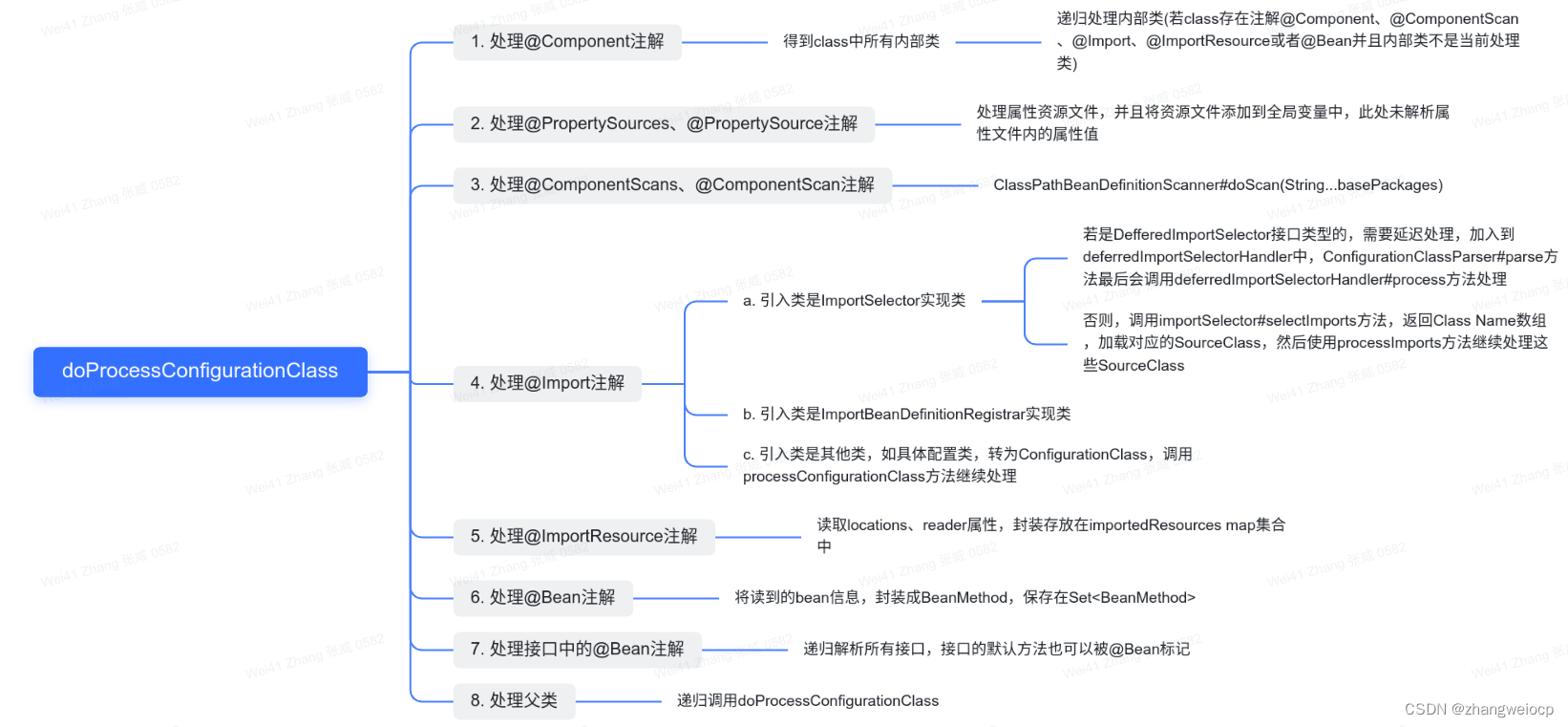
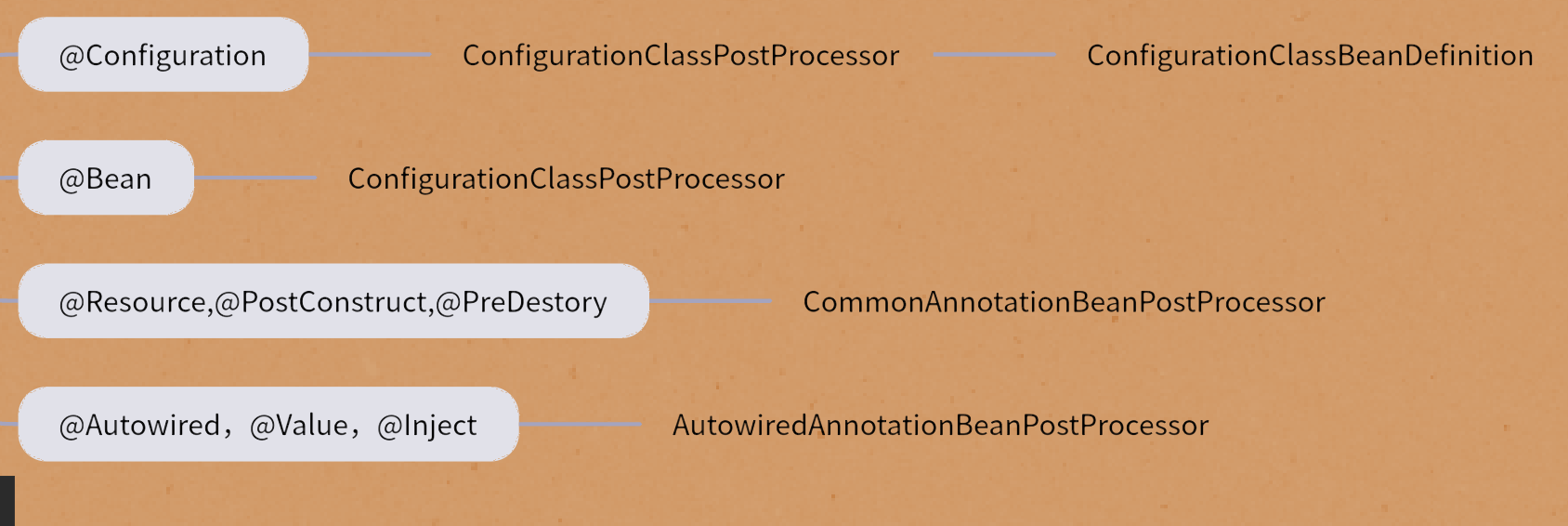
上文提到Spring在Bean扫描过程中,会手动将5个Processor类注册到beanDefinitionMap中,其中ConfigurationClassPostProcessor就是本文将要讲解的内容,该类会在refresh()方法中通过调用invokeBeanFactoryPosstProcessors(beanFactory)被调用。 5…...
Android OpenGL ES 2.0入门实践
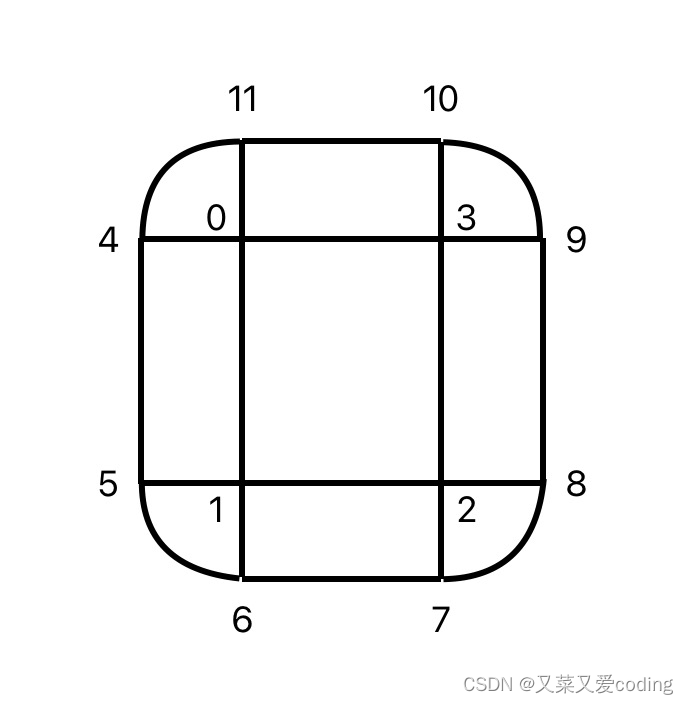
本文既然是入门实践,就先从简单的2D图形开始,首先,参考两篇官方文档搭建个框架,便于写OpenGL ES相关的代码:构建 OpenGL ES 环境、OpenGL ES 2.0 及更高版本中的投影和相机视图。 先上代码,代码效果如下图…...

sql语句性能进阶必须了解的知识点——索引失效分析
在前面的文章中讲解了sql语句的优化策略 sql语句性能进阶必须了解的知识点——sql语句的优化方案-CSDN博客 sql语句的优化重点还有一处,那就是—— 索引!好多sql语句慢的本质原因就是设置的索引失效或者根本没有建立索引!今天我们就来总结一…...
ctfhub技能树web题目全解
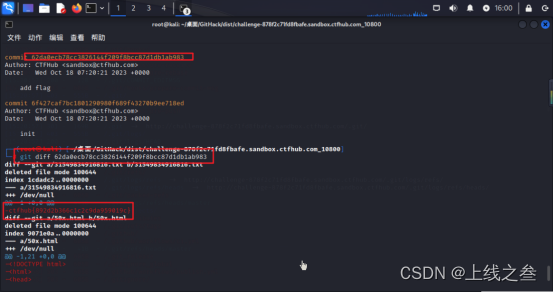
Rce 文件包含 靶场环境 重点是这个代码,strpos,格式是这样的strpoc(1,2,3) 1是要搜索的字符串,必须有;2是要查询的字符串,必须有;3是在何处开始查询&#…...

AMD、CMD、UMD是什么?
AMD(Asynchronous Module Definition)、CMD(Common Module Definition)和UMD(Universal Module Definition)是JavaScript模块化规范,用于管理和组织JavaScript代码的模块化加载和依赖管理。 1:AMD(异步模块定义): AMD是由RequireJS提出的模块化规范。它支持异步加载…...

AM@微分方程相关概念@线性微分方程@一阶线性微分方程的通解
文章目录 abstract引言 一般的微分方程常微分方程微分方程的解隐式解通解和特解初始条件初值问题微分方程的积分曲线 线性微分方程一阶线性微分方程一阶齐次和非齐次线性微分方程一阶齐次线性微分方程的解一阶非齐次线性微分方程的解 abstract AM微分方程相关概念线性微分方程…...

基于深度学习的安全帽识别检测系统(python OpenCV yolov5)
收藏和点赞,您的关注是我创作的动力 文章目录 概要 一、研究的内容与方法二、基于深度学习的安全帽识别算法2.1 深度学习2.2 算法流程2.3 目标检测算法2.3.1 Faster R-CNN2.3.2 SSD2.3.3 YOLO v3 三 实验与结果分析3.1 实验数据集3.1.1 实验数据集的构建3.1.2 数据…...
Spring源码分析篇一 @Autowired 是怎样完成注入的?究竟是byType还是byName亦两者皆有
1. 五种不同场景下 Autowired 的使用 第一种情况 上下文中只有一个同类型的bean 配置类 package org.example.bean;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration;Configuration public class FruitCo…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
