把两个4点的结构相加
( A, B )---3*30*2---( 1, 0 )( 0, 1 )
让网络的输入只有3个节点,训练集中只有5张图片,让A中有4个1,B全是0,排列组合,统计迭代次数并排序。
其中有3个结构
| 3差值结构 | 迭代次数 | 4差值结构 | 迭代次数 | 3+1 | ||||||||
| 3-2 | 0 | 1 | 0 | 30302.2 | 5 | - | - | 1 | 20004.9 | 2 | 3 | |
| 0 | 1 | 0 | 30302.2 | 5 | 1 | - | - | 20004.9 | 2 | 3 | ||
| 0 | 1 | 0 | 30302.2 | 5 | 1 | - | - | 20004.9 | 2 | 3 | ||
| 0 | 0 | 0 | 30302.2 | 5 | - | - | - | 20004.9 | 2 | 3 | ||
| 0 | 0 | 0 | 30302.2 | 5 | 1 | - | - | 20004.9 | 2 | 3 | ||
| 5 | 20004.9 | 2 | 3 | |||||||||
| 3-3 | 0 | 0 | 1 | 30392.1 | 6 | - | - | - | 22075 | 2 | ||
| 0 | 1 | 0 | 30392.1 | 6 | - | 1 | - | 22075 | 2 | |||
| 0 | 0 | 1 | 30392.1 | 6 | - | 1 | - | 22075 | 2 | |||
| 0 | 0 | 0 | 30392.1 | 6 | - | 1 | - | 22075 | 2 | |||
| 0 | 0 | 0 | 30392.1 | 6 | - | 1 | - | 22075 | 2 | |||
| 6 | 22075 | 2 | ||||||||||
| 8 | - | - | 1 | 28209.1 | 3 | |||||||
| 8 | - | - | 1 | 28209.1 | 3 | |||||||
| 8 | - | 1 | - | 28209.1 | 3 | |||||||
| 8 | - | - | - | 28209.1 | 3 | |||||||
| 8 | - | 1 | - | 28209.1 | 3 | |||||||
| 8 | 28209.1 | 3 | ||||||||||
4a5,4a6,4a8,
用3+1的方式表示这3个结构
4a5=3a2+1=3a3+1
4a6=3a2+1
4a8=3a3+1
4a5减少一个点得到3a2或3a3,而4a6减少一个点得到3a2,4a8减少一个点得到3a3.因此有等式
2*4a5=4a6+4a8
| 5-1 | |||||||||||||||
| 6 | 19 | 19 | 25 | 19 | 19 | 10 | 19 | 25 | |||||||
| 6 | 19 | 19 | 25 | 19 | 19 | 10 | 19 | 25 | |||||||
| 6 | 10 | 10 | 1 | 10 | 10 | 10 | 19 | 25 | |||||||
| 6 | 10 | 10 | 1 | 10 | 10 | 10 | 19 | 25 | |||||||
| 6 | 10 | 10 | 1 | 10 | 10 | 10 | 19 | 25 | |||||||
| 6 | 10 | 10 | 1 | 10 | 10 | 10 | 19 | 25 | |||||||
| 6 | 19 | 19 | 25 | 19 | 19 | 10 | 19 | 25 | |||||||
| 6 | 19 | 19 | 25 | 19 | 19 | 10 | 19 | 25 | |||||||
| 6 | 10 | 19 | 25 | ||||||||||||
| 6 | 10 | 19 | 25 | ||||||||||||
| 8 | 31 | 31 | 31 | 27 | 27 | 31 | 31 | 31 | 1 | 9 | 27 | 31 | |||
| 8 | 31 | 31 | 31 | 27 | 27 | 31 | 31 | 31 | 1 | 9 | 27 | 31 | |||
| 8 | 9 | 9 | 9 | 1 | 1 | 9 | 9 | 9 | 1 | 9 | 27 | 31 | |||
| 8 | 9 | 9 | 9 | 1 | 1 | 9 | 9 | 9 | 1 | 9 | 27 | 31 | |||
| 8 | 9 | 9 | 9 | 1 | 1 | 9 | 9 | 9 | 1 | 9 | 27 | 31 | |||
| 8 | 9 | 9 | 9 | 1 | 1 | 9 | 9 | 9 | 1 | 9 | 27 | 31 | |||
| 8 | 31 | 31 | 31 | 27 | 27 | 31 | 31 | 31 | 1 | 9 | 27 | 31 | |||
| 8 | 31 | 31 | 31 | 27 | 27 | 31 | 31 | 31 | 1 | 9 | 27 | 31 | |||
| 8 | 1 | 9 | 27 | 31 | |||||||||||
| 8 | 1 | 9 | 27 | 31 |
但是从5-1的角度,4a6把空间分成4a10,4a19,4a25;4a8把空间分成4a1,4a9,4a27,4a31.但是并没有哪个4个点的结构可以正好把空间分成5a1,5a9,5a10,5a19,5a25,5a27,5a31这7个部分,所以等式2*4a5=4a6+4a8在5-1方向上是不成立的。
有8个人在操场上排队,两两一组,(1,2),(3,4),(5,6),(7,8)如果1,3,5,7希望队伍对空间的分割方式为4a6,而2,4,6,8希望队伍对空间的分割的方式为4a8,这个问题没有解,但是如果这两组坚决不妥协到底会发生什么?
因为1,3,5,7希望把空间分割成5a10,5a19,5a25,这3种情况,但是因为他们只有4个点,因此4个点的分布应该是5a10-1,5a19-1,5a25-1.同样2,4,6,8如果执意坚持不肯妥协队伍应该变成5a1-1,5a9-1,5a27-1,5a31-1.
因为
| 5差值结构 | 迭代次数 | 4+1 | ||||||||||||||||
| 8 | 5 | 1 | 0 | 1 | 1 | 3684 | 1 | 3 | 5 | 8 | ||||||||
| 1 | 0 | 0 | 1 | 0 | 3684 | 1 | 3 | 5 | 8 | |||||||||
| 1 | 0 | 0 | 1 | 0 | 3684 | 1 | 3 | 5 | 8 | |||||||||
| 0 | 3 | 0 | 0 | 1 | 3684 | 1 | 3 | 5 | 8 | |||||||||
| 0 | 0 | 0 | 0 | 0 | 3684 | 1 | 3 | 5 | 8 | |||||||||
| 3684 | 1 | 3 | 5 | 8 | ||||||||||||||
| 8 | 7 | 0 | 9 | 1 | 1 | 0 | 11768 | 2 | 7 | 8 | 11 | |||||||
| 0 | 0 | 2 | 0 | 0 | 1 | 11768 | 2 | 7 | 8 | 11 | ||||||||
| 0 | 0 | 2 | 0 | 0 | 1 | 11768 | 2 | 7 | 8 | 11 | ||||||||
| 0 | 11 | 0 | 0 | 1 | 0 | 11768 | 2 | 7 | 8 | 11 | ||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 11768 | 2 | 7 | 8 | 11 | ||||||||
| 2 | 7 | 8 | 11 | |||||||||||||||
| 6 | 5 | 10 | 0 | 1 | 1 | 12410 | 3 | 5 | 6 | |||||||||
| 0 | 3 | 0 | 0 | 1 | 12410 | 3 | 5 | 6 | ||||||||||
| 0 | 3 | 0 | 0 | 1 | 12410 | 3 | 5 | 6 | ||||||||||
| 0 | 3 | 0 | 0 | 1 | 12410 | 3 | 5 | 6 | ||||||||||
| 0 | 0 | 0 | 0 | 0 | 12410 | 3 | 5 | 6 | ||||||||||
| 3 | 5 | 6 | ||||||||||||||||
| 0 | 6 | 19 | 0 | 0 | 1 | 23659 | 5 | 6 | ||||||||||
| 5 | 0 | 0 | 1 | 0 | 23659 | 5 | 6 | |||||||||||
| 5 | 0 | 0 | 1 | 0 | 23659 | 5 | 6 | |||||||||||
| 5 | 0 | 0 | 1 | 0 | 23659 | 5 | 6 | |||||||||||
| 5 | 0 | 0 | 1 | 0 | 23659 | 5 | 6 | |||||||||||
| 5 | 6 | |||||||||||||||||
| 6 | 25 | 1 | 0 | 0 | 27184 | 6 | ||||||||||||
| 6 | 1 | 0 | 0 | 27184 | 6 | |||||||||||||
| 6 | 1 | 0 | 0 | 27184 | 6 | |||||||||||||
| 6 | 1 | 0 | 0 | 27184 | 6 | |||||||||||||
| 6 | 1 | 0 | 0 | 27184 | 6 | |||||||||||||
| 6 | ||||||||||||||||||
| 8 | 0 | 27 | 1 | 0 | 0 | 29172 | 5 | 8 | ||||||||||
| 8 | 0 | 1 | 0 | 0 | 29172 | 5 | 8 | |||||||||||
| 8 | 0 | 1 | 0 | 0 | 29172 | 5 | 8 | |||||||||||
| 0 | 5 | 0 | 1 | 0 | 29172 | 5 | 8 | |||||||||||
| 0 | 5 | 0 | 1 | 0 | 29172 | 5 | 8 | |||||||||||
| 5 | 8 | |||||||||||||||||
| 8 | 0 | 0 | 31 | 1 | 0 | 0 | 33688 | 7 | 8 | |||||||||
| 0 | 7 | 0 | 0 | 1 | 0 | 33688 | 7 | 8 | ||||||||||
| 0 | 0 | 7 | 0 | 0 | 1 | 33688 | 7 | 8 | ||||||||||
| 0 | 7 | 0 | 0 | 1 | 0 | 33688 | 7 | 8 | ||||||||||
| 0 | 0 | 7 | 0 | 0 | 1 | 33688 | 7 | 8 | ||||||||||
| 7 | 8 | |||||||||||||||||
得到加法关系
5a1=4a1+1=4a3+1=4a5+1=4a8+1
5a9=4a2+1=4a7+1=4a8+1=4a11+1
5a10=4a3+1=4a5+1=4a6+1
5a19=4a5+1=4a6+1
5a25=4a6+1
5a27=4a5+1=4a8+1
5a31=4a7+1=4a8+1
所以在5-1的方向上最终得到的是一个由4a1,4a2,4a3,4a5,4a6,4a7,4a8,4a11共8个状态构成的复合态。
4a6+4a8→4a1+4a2+4a3+4a5+4a6+4a7+4a8+4a11
3+1的方向回答的是这个结构是由什么构成的,5-1回答的是这个结构可以构成什么,计算表明4a6+4a8这两个结构的和在两个方向上的结果并不相同。 3+1方向上4a6和4a8的和是稳定的,在5-1方向上他们的和是在8个状态之间不断的振荡。
相关文章:

把两个4点的结构相加
( A, B )---3*30*2---( 1, 0 )( 0, 1 ) 让网络的输入只有3个节点,训练集中只有5张图片,让A中有4个1,B全是0,排列组合,统计迭代次数并排序。 其中有3个结构 3差值结构 迭代次数 4差值结构 迭代次数 31 3-2 0 1 …...
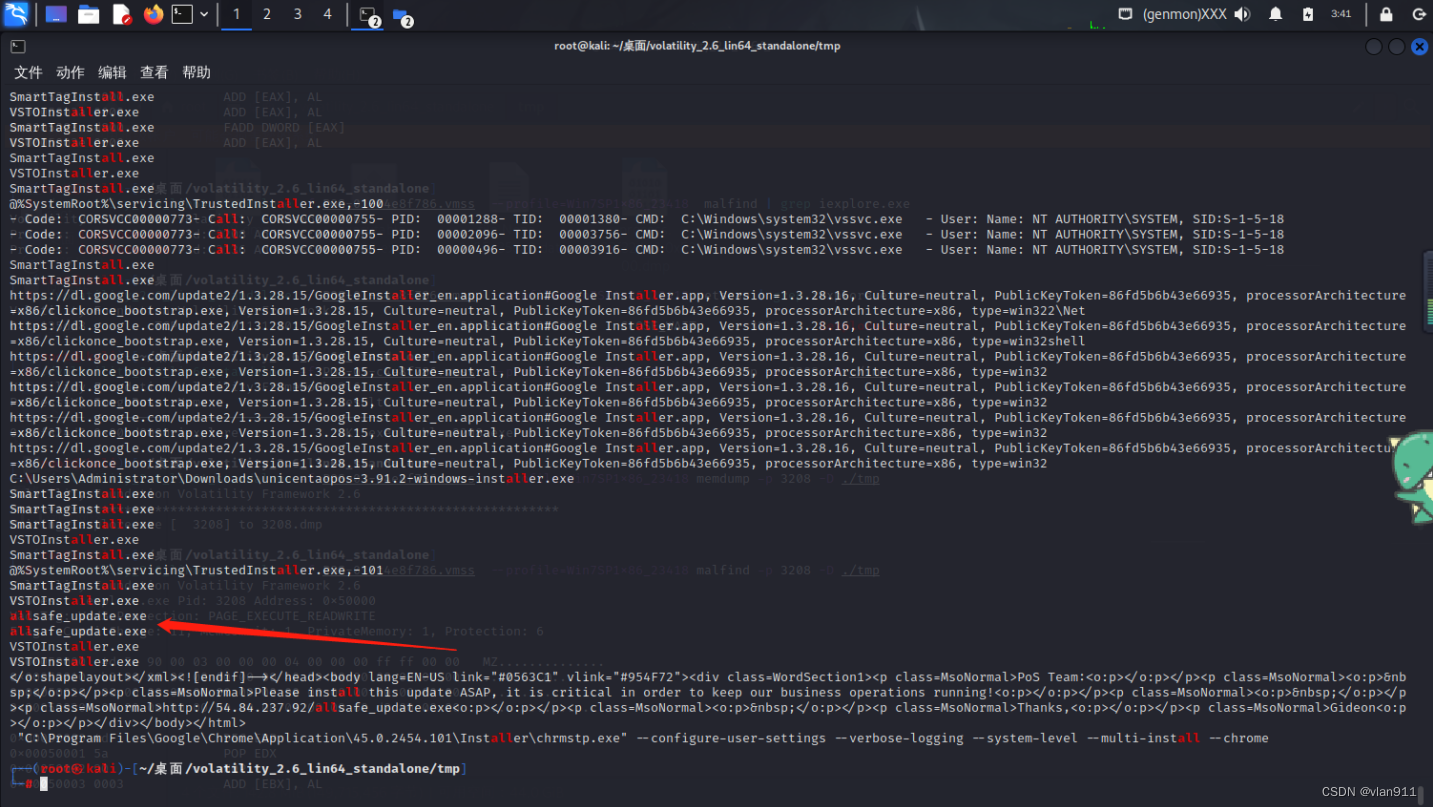
windows内存取证-中等难度-下篇
上文我们对第一台Target机器进行内存取证,今天我们继续往下学习,内存镜像请从上篇获取,这里不再进行赘述 Gideon 攻击者访问了“Gideon”,他们向AllSafeCyberSec域控制器窃取文件,他们使用的密码是什么? 攻击者执…...

代码随想录算法训练营第7天|454 四数相加II 383. 赎金信 15.三数之和 18 四数之和
JAVA代码编写 454. 四数相加 II 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < nnums1[i] nums2[j] nums3[k] nums4[l] 0 示例 1:…...
负载均衡深度解析:算法、策略与Nginx实践
引言 如今,网站和应用服务面临着巨大的访问流量,如何高效、稳定地处理这些流量成为了一个亟待解决的问题。负载均衡技术因此应运而生,它通过将流量合理分配到多个服务器上,不仅优化了资源的利用率,还大大提升了系统的…...

7. 一文快速学懂常用工具——Makefile
本章讲解知识点 引言MakefileMakefile 入门本专栏适合于软件开发刚入职的学生或人士,有一定的编程基础,帮助大家快速掌握工作中必会的工具和指令。本专栏针对面试题答案进行了优化,尽量做到好记、言简意赅。如专栏内容有错漏,欢迎在评论区指出或私聊我更改,一起学习,共同…...

[ACTF2023]复现
MDH 源题: from hashlib import sha256 from secret import flagr 128 c 96 p 308955606868885551120230861462612873078105583047156930179459717798715109629 Fp GF(p)def gen():a1 random_matrix(Fp, r, c)a2 random_matrix(Fp, r, c)A a1 * a2.Treturn…...
HNU-编译原理-讨论课1
讨论课安排:2次4学时,分别完成四大主题讨论 分组:每个班分为8组,每组4~5人,自选组长1人 要求和说明: 以小组为单位上台报告;每次每组汇报2个小主题,每组按要求在2个小主题中各选1…...

【Linux】关于Nginx的详细使用,部署项目
前言: 今天小编给大家带来的是关于Nginx的详细使用,部署项目,希望可以给正在学习,工作的你带来有效的帮助! 一,Nginx简介 Nginx是一个高性能的开源Web服务器和反向代理服务器。它最初由Igor Sysoev在2004年…...

编写 navigation2 控制器插件
简介 本教程展示了如何创建自己的控制器插件。在本教程中,我们将基于这篇论文实现纯追踪路径跟踪算法。建议您阅读该论文。 注意:本教程基于 Nav2 堆栈中以前存在的简化版本的 Regulated Pure Pursuit 控制器。您可以在此处找到与本教程相匹配的源代…...

计算机网络 第六章应用层
文章目录 1 应用层功能概述2 网络应用模型:客户服务器(CS)3 网络应用模型:PeerToPeer(P2P)4 域名和域名系统5 常见域名解析服务器6 两种域名解析过程7 什么是FTP8 FTP的工作原理9 EMail的组成 1 应用层功能概述 2 网络应用模型:客户服务器(CS…...
)
人工智能领域CCF推荐国际学术刊物最新目录(全)
2021年1月,CCF决定启动新一轮中国计算机学会推荐国际学术会议和期刊目录调整工作并委托CCF学术工作委员会组织实施。 2023年3月8日, 中国计算机学会正式发布了2022版《中国计算机学会推荐国际学术会议和期刊目录》(以下简称《目录》) 。 相较于上一版目录࿰…...

实现基于 Azure DevOps 的数据库 CI/CD 最佳实践
数据库变更一直是整个应用发布过程中效率最低、流程最复杂、风险最高的环节,也是 DevOps 流程中最难以攻克的阵地。那我们是否能在具体的 CI/CD 流程中,像处理代码那样处理数据库变更呢? DORA 调研报告 DORA(DevOps Research &am…...

上海实习小记
8月3日入职10月27日离职,原本还想做满3个月再走,可惜公司提早要迁到成都,就只好 离职了回学校了。在博客随便写写记录一下这几个月的生活吧,想到哪里写到哪里 实习的公司是一个小公司,开发一款类似于咸鱼之王的游戏&am…...

uniapp实现路线规划
UniApp是一个基于Vue.js框架开发的跨平台应用开发框架,可以同时构建iOS、Android、H5等多个平台的应用。它使用了基于前端技术栈的Web开发方式,通过编写一套代码,即可在不同平台上运行和发布应用。 UniApp具有以下特点: 跨平台开…...

飞利浦双串口51单片机485网关
主要功能将PC端的数据接收下来,分发到不同的设备,也是轮询设备数据读取回来,打包回传到PC端,数据包包头包尾识别,数据校验,接收超时处理,将协议结构化处理,协议的改动不需要改动程序…...
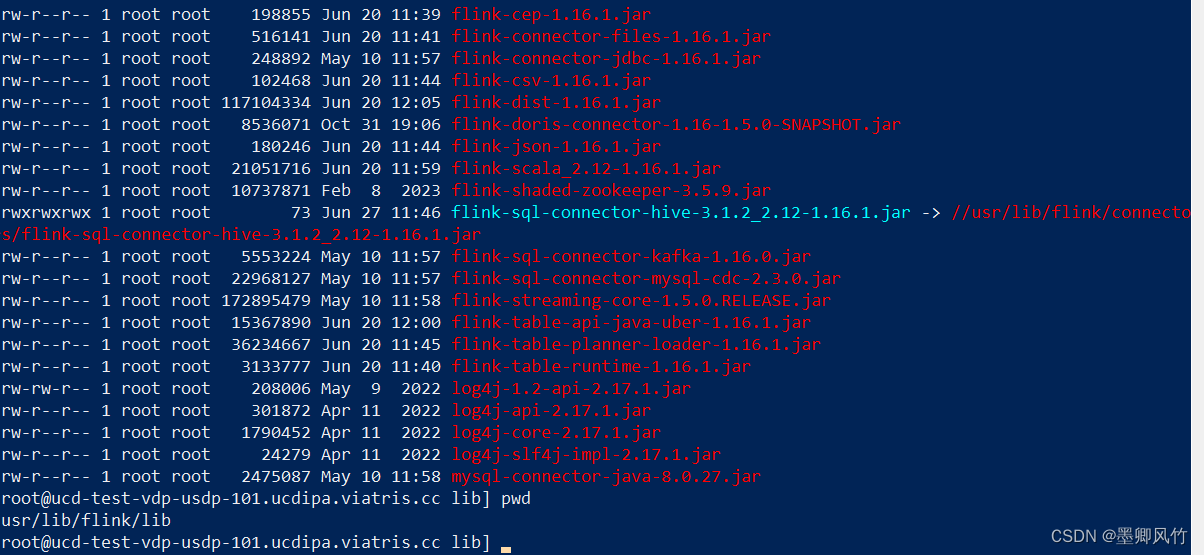
生态扩展:Flink Doris Connector
生态扩展:Flink Doris Connector 官网地址: https://doris.apache.org/zh-CN/docs/dev/ecosystem/flink-doris-connector flink的安装: tar -zxvf flink-1.16.0-bin-scala_2.12.tgz mv flink-1.16.0-bin-scala_2.12.tgz /opt/flinkflink环境…...

HarmonyOS(二)—— 初识ArkTS开发语言(上)之TypeScript入门
前言 Mozilla创造了JS,Microsoft创建了TS,而Huawei进一步推出了ArkTS。因此在学习使用ArkTS前,需要掌握基本的TS开发技能。 ArkTS介绍 ArkTS是HarmonyOS优选的主力应用开发语言。它在TypeScript(简称TS)的基础上&am…...
从零开始实现神经网络(一)_NN神经网络
参考文章:神经网络介绍 一、神经元 这一神经网络的基本单元,神经元接受输入,对它们进行一些数学运算,并产生一个输出。 这里有三步。 首先,将每个输入(X1)乘以一个权重: 接下来&…...

C语言 每日一题 Day10
1.使用函数判断完全平方数 本题要求实现一个判断整数是否为完全平方数的简单函数。 函数接口定义: int IsSquare(int n); 其中n是用户传入的参数,在长整型范围内。如果n是完全平方数,则函数IsSquare必须返回1,否则返回0。 代码实…...
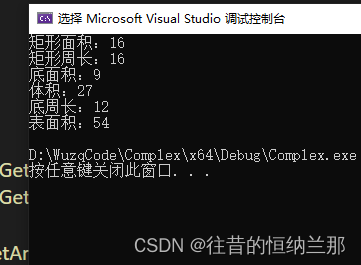
C++继承——矩形和长方体
Rectangle矩形类 /*矩形类*/ class Rectangle { private:double L 0;double W 0; public:Rectangle() default;Rectangle(double a, double b);double GetArea(); /*矩形面积*/double GetGirth(); /*矩形周长*/ }; /*构造函数*/ Rectangle::Rectangle(double a, double b) …...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
