AM@二阶常系数非齐次线性微分方程@待定系数法可解决的经典类型1
文章目录
- abstract
- 二阶常系数非齐次线性微分方程
- 待定系数法可解类型
- 类型1
- 小结
- 例
abstract
- 二阶常系数非齐次线性微分方程
- 待定系数法可解决的经典类型1及其解法总结与应用
- 本文给出类型1为什么可以通过待定求出特解,并且待定函数要设成什么形式
- 推理过程有一定工作量,而在应用中只需要记住可以用待定系数法求解,以及待定系数函数的形式公式以及公式中各部分的确定方法即可
二阶常系数非齐次线性微分方程
-
二阶常系数非齐次线性微分方程的一般形式为 y ′ ′ + p y ′ + q y = f ( x ) y''+py'+qy=f(x) y′′+py′+qy=f(x)
(1),其中 p , q p,q p,q是常数 -
求方程(1)的通解,归结为求对应齐次方程: y ′ ′ + p y ′ + q y = 0 y''+py'+qy=0 y′′+py′+qy=0
(2)的通解 Y ( x ) Y(x) Y(x)和一个(1)的特解 y ∗ ( x ) y^*(x) y∗(x);则 Y ( x ) + y ∗ ( x ) Y(x)+y^*(x) Y(x)+y∗(x)为(1)的通解 -
对于非齐次的二阶常系数线性微分方程,仅有限的类型(以 f ( x ) f(x) f(x)的不同类型作区分)是容易解决的,这里介绍两种类型
待定系数法可解类型
- 当 f ( x ) f(x) f(x)取两种特殊类型的函数时,可以不用积分的方法求 y ∗ y^* y∗,而是通过待定系数法
- 两种形式分别为:
- f ( x ) = e λ x P m ( x ) f(x)=e^{\lambda{x}}P_{m}(x) f(x)=eλxPm(x), f ( x ) f(x) f(x)= e λ x ( P l ( x ) cos ω x + P n ( x ) sin ω x ) e^{\lambda{x}}(P_{l}(x)\cos{\omega}x+P_{n}(x)\sin{\omega{x}}) eλx(Pl(x)cosωx+Pn(x)sinωx)
类型1
-
当 f ( x ) f(x) f(x)= e λ x P m ( x ) e^{\lambda{x}}P_{m}(x) eλxPm(x)
(2),其中 λ \lambda λ是常数, P m ( x ) P_{m}(x) Pm(x)为 x x x的一个** m m m次**多项式(设为 ∑ i = 0 m a i x i \sum_{i=0}^{m}a_ix^{i} ∑i=0maixi)- 此时方程(1)表示为 y ′ ′ + p y ′ + q y y''+py'+qy y′′+py′+qy= e λ x P m ( x ) e^{\lambda{x}}P_{m}(x) eλxPm(x)
(2-1)- 当 λ = 0 \lambda=0 λ=0时, f ( x ) = P m ( x ) f(x)=P_m(x) f(x)=Pm(x),方程(2-1)进一步改写为 y ′ ′ + p y ′ + q y y''+py'+qy y′′+py′+qy= P m ( x ) P_{m}(x) Pm(x)
(2-2)
- 当 λ = 0 \lambda=0 λ=0时, f ( x ) = P m ( x ) f(x)=P_m(x) f(x)=Pm(x),方程(2-1)进一步改写为 y ′ ′ + p y ′ + q y y''+py'+qy y′′+py′+qy= P m ( x ) P_{m}(x) Pm(x)
- 对式(2)求导
- f ′ ( x ) f'(x) f′(x)= λ e λ x P m ( x ) \lambda e^{\lambda{x}}P_{m}(x) λeλxPm(x)+ e λ x P m ′ ( x ) e^{\lambda{x}}P_{m}'(x) eλxPm′(x)= e λ x ( λ P m ( x ) + P m ′ ( x ) ) e^{\lambda{x}}(\lambda{P_{m}(x)}+P_{m}'(x)) eλx(λPm(x)+Pm′(x))其中 Q m = λ P m ( x ) + P m ′ ( x ) Q_{m}=\lambda{P_{m}(x)}+P_{m}'(x) Qm=λPm(x)+Pm′(x)仍然是 m m m次多项式,继续求高阶导数,得到相仿的结论,即
- f ( n ) ( x ) f^{(n)}(x) f(n)(x)= e λ x Q m [ n ] ( x ) e^{\lambda{x}}Q_{m}^{[n]}(x) eλxQm[n](x),其中 Q m [ n ] ( x ) Q_{m}^{[n]}(x) Qm[n](x)表示 f ( x ) f(x) f(x)第 n n n阶导数包含的 m m m阶多项式
- 此类型的特点是,多项式函数和指数型函数的乘积的导数仍然是多项式函数和指数型函数的乘积,再官产方程(2-1),这恰好可以并为等号右端形式,即 e λ x P m ( x ) e^{\lambda{x}}P_{m}(x) eλxPm(x)
- f ′ ( x ) f'(x) f′(x)= λ e λ x P m ( x ) \lambda e^{\lambda{x}}P_{m}(x) λeλxPm(x)+ e λ x P m ′ ( x ) e^{\lambda{x}}P_{m}'(x) eλxPm′(x)= e λ x ( λ P m ( x ) + P m ′ ( x ) ) e^{\lambda{x}}(\lambda{P_{m}(x)}+P_{m}'(x)) eλx(λPm(x)+Pm′(x))其中 Q m = λ P m ( x ) + P m ′ ( x ) Q_{m}=\lambda{P_{m}(x)}+P_{m}'(x) Qm=λPm(x)+Pm′(x)仍然是 m m m次多项式,继续求高阶导数,得到相仿的结论,即
- 由此可以推测 y ∗ y^* y∗= Q ( x ) e λ x Q(x)e^{\lambda{x}} Q(x)eλx
(3)可能是方程(1)的特解[待定系数法]- 其中 Q ( x ) Q(x) Q(x)是某个多项式
- 对(3)求导, y ∗ ′ y^{*'} y∗′= Q ′ ( x ) e λ x Q'(x)e^{\lambda{x}} Q′(x)eλx+ Q ( x ) λ e λ x Q(x)\lambda{e^{\lambda{x}}} Q(x)λeλx= e λ x ( Q ′ ( x ) + Q ( x ) λ ) e^{\lambda{x}}(Q'(x)+Q(x)\lambda) eλx(Q′(x)+Q(x)λ)
(3-1)- y ∗ ′ ′ y^{*''} y∗′′= λ e λ x ( ( Q ′ ( x ) + Q ( x ) λ ) \lambda e^{\lambda{x}}((Q'(x)+Q(x)\lambda) λeλx((Q′(x)+Q(x)λ)+ e λ x ( Q ′ ′ ( x ) + λ Q ′ ( x ) ) e^{\lambda{x}}(Q''(x)+\lambda Q'(x)) eλx(Q′′(x)+λQ′(x))= e λ x ( λ 2 Q ( x ) + 2 λ Q ′ ( x ) + Q ′ ′ ( x ) ) e^{\lambda{x}}(\lambda^2{Q(x)}+2\lambda{Q'(x)}+Q''(x)) eλx(λ2Q(x)+2λQ′(x)+Q′′(x))
(3-2)
- y ∗ ′ ′ y^{*''} y∗′′= λ e λ x ( ( Q ′ ( x ) + Q ( x ) λ ) \lambda e^{\lambda{x}}((Q'(x)+Q(x)\lambda) λeλx((Q′(x)+Q(x)λ)+ e λ x ( Q ′ ′ ( x ) + λ Q ′ ( x ) ) e^{\lambda{x}}(Q''(x)+\lambda Q'(x)) eλx(Q′′(x)+λQ′(x))= e λ x ( λ 2 Q ( x ) + 2 λ Q ′ ( x ) + Q ′ ′ ( x ) ) e^{\lambda{x}}(\lambda^2{Q(x)}+2\lambda{Q'(x)}+Q''(x)) eλx(λ2Q(x)+2λQ′(x)+Q′′(x))
- 将(3,3-1,3-2)代入方程(2-1),得 e λ x ( λ 2 Q ( x ) + 2 λ Q ′ ( x ) + Q ′ ′ ( x ) ) e^{\lambda{x}}(\lambda^2{Q(x)}+2\lambda{Q'(x)}+Q''(x)) eλx(λ2Q(x)+2λQ′(x)+Q′′(x))+ p e λ x ( Q ′ ( x ) + Q ( x ) λ ) pe^{\lambda{x}}(Q'(x)+Q(x)\lambda) peλx(Q′(x)+Q(x)λ)+ q Q ( x ) e λ x qQ(x)e^{\lambda{x}} qQ(x)eλx= e λ x P m ( x ) e^{\lambda{x}}P_{m}(x) eλxPm(x),整理得 Q ′ ′ ( x ) + ( 2 λ + p ) Q ′ ( x ) + ( λ 2 + p λ + q ) Q ( x ) Q''(x)+(2\lambda+p)Q'(x)+(\lambda^2+p\lambda+q)Q(x) Q′′(x)+(2λ+p)Q′(x)+(λ2+pλ+q)Q(x)= P m ( x ) P_{m}(x) Pm(x)
(4)
- 此时方程(1)表示为 y ′ ′ + p y ′ + q y y''+py'+qy y′′+py′+qy= e λ x P m ( x ) e^{\lambda{x}}P_{m}(x) eλxPm(x)
-
根据 λ \lambda λ与方程(1)的特征方程 ( r 2 + p r + q = 0 ) (r^2+pr+q=0) (r2+pr+q=0)
(5)的根(特征根)关系,分为:不是特征根,单根,重根,这三种情形讨论-
若 λ \lambda λ不是(5)的根,则 λ 2 + p λ + q ≠ 0 \lambda^2+p\lambda+q\neq{0} λ2+pλ+q=0
(5-1),- 由于 P m ( x ) P_{m}(x) Pm(x)是 m m m次多项式,要使(4)式两边相等,则 Q ( x ) Q(x) Q(x)必须也是 m m m次多项式,记为 Q ( x ) = Q m ( x ) Q(x)=Q_{m}(x) Q(x)=Qm(x)= ∑ i = 0 m b i x i \sum_{i=0}^{m}b_ix^{i} ∑i=0mbixi
(6) - 将(6)代入方程(4),比较两边同次幂的系数,得到 0 ∼ m 0\sim{m} 0∼m次共 m + 1 m+1 m+1个方程
- 解这 m + 1 m+1 m+1个方程,可得 b 0 , ⋯ , b m b_0,\cdots,b_m b0,⋯,bm
- 代入(3),从而得到(2-1)的特解
- 由于 P m ( x ) P_{m}(x) Pm(x)是 m m m次多项式,要使(4)式两边相等,则 Q ( x ) Q(x) Q(x)必须也是 m m m次多项式,记为 Q ( x ) = Q m ( x ) Q(x)=Q_{m}(x) Q(x)=Qm(x)= ∑ i = 0 m b i x i \sum_{i=0}^{m}b_ix^{i} ∑i=0mbixi
-
若 λ \lambda λ是(5)的单根(两个互异根中的一个),则 λ 2 + p λ + q = 0 \lambda^2+p\lambda+q={0} λ2+pλ+q=0
(6-1)-
此处 λ \lambda λ是单根,设另一根是 λ ‾ \overline\lambda λ;由韦达定理: λ + λ ‾ = − p \lambda+\overline{\lambda}=-p λ+λ=−p,而 λ + λ ≠ λ + λ ‾ \lambda+\lambda\neq{\lambda+\overline{\lambda}} λ+λ=λ+λ,所以 2 λ ≠ − p 2\lambda\neq{-p} 2λ=−p,即 2 λ + p ≠ 0 2\lambda+p\neq{0} 2λ+p=0
(7) -
此时方程(4)改写为 Q ′ ′ ( x ) + ( 2 λ + p ) Q ′ ( x ) Q''(x)+(2\lambda+p)Q'(x) Q′′(x)+(2λ+p)Q′(x)= P m ( x ) P_{m}(x) Pm(x);因此 Q ′ ( x ) Q'(x) Q′(x)必须是 m m m次多项式;相应的, Q ( x ) Q(x) Q(x)就得是 m + 1 m+1 m+1次多项式
-
令 Q ( x ) = x Q m ( x ) Q(x)=xQ_m(x) Q(x)=xQm(x)
(8);仍然可以用系数比较法确定出 Q m ( x ) Q_{m}(x) Qm(x)的系数 b 0 , b 1 , ⋯ , b m b_0,b_1,\cdots,b_m b0,b1,⋯,bm;就可以得出 Q m ( x ) Q_m(x) Qm(x),代入(8)得出 Q ( x ) Q(x) Q(x),再代入(3),得方程(2-1)的特解
-
-
若 λ \lambda λ是(5)的重根,此是也有(6-1)成立,并且 2 λ + p = 0 2\lambda+p=0 2λ+p=0
(8-1)- 此时方程(4)改写为 Q ′ ′ ( x ) = P m ( x ) Q''(x)=P_{m}(x) Q′′(x)=Pm(x)
- 要使方程(4)两端恒等,必有 Q ′ ′ ( x ) Q''(x) Q′′(x)为 m m m次多项式,从而可以令 Q ( x ) = x 2 Q m ( x ) Q(x)=x^2Q_{m}(x) Q(x)=x2Qm(x)
- 同样使用系数比较法确定出 Q m ( x ) Q_{m}(x) Qm(x)的系数,从而得出 Q ( x ) Q(x) Q(x),最后代入(3)得出(2-1)的特解
-
-
上述类型1的结论可知,方程(1)确实可以使用待定系数法求特解,该特解可以设为 y ∗ y^* y∗= x k Q m ( x ) e λ x x^kQ_{m}(x)e^{\lambda{x}} xkQm(x)eλx,并且保证这个待定形式是可求解且正确的👺
小结
- 二阶常系数非齐次线性微分方程 y ′ ′ + p y ′ + q y y''+py'+qy y′′+py′+qy= P m ( x ) e λ x P_m(x)e^{\lambda{x}} Pm(x)eλx
(1)具有形如 y ∗ = x k Q m ( x ) e λ x y^*=x^kQ_{m}(x)e^{\lambda{x}} y∗=xkQm(x)eλx的特解, ( k = 0 , 1 , 2 ) (k=0,1,2) (k=0,1,2)- 其中 Q m ( x ) Q_{m}(x) Qm(x), P m ( x ) P_m(x) Pm(x)是同为 m m m次多项式, Q m ( x ) Q_{m}(x) Qm(x)的 m + 1 m+1 m+1个系数由系数比较法构造 m + 1 m+1 m+1个方程分别求出
- k k k按照 λ \lambda λ是方程(1)的特征方程 r 2 + p r + q = 0 r^2+pr+q=0 r2+pr+q=0
(2)的根的重数决定的,- 0 0 0重根, k = 0 k=0 k=0;(表示 λ \lambda λ不是方程(2)的根的简称)
- 1 1 1重根, k = 1 k=1 k=1
- 2 2 2重根, k = 2 k=2 k=2
例
- 求 y ′ ′ − 2 y ′ − 3 y y''-2y'-3y y′′−2y′−3y= 3 x + 1 3x+1 3x+1
(1)的一个特解- 方程类型分析:方程(1)是常系数非齐次线性微分方程中的经典类型1
- 令 f ( x ) f(x) f(x)= 3 x + 1 3x+1 3x+1= e 0 x ( 3 x + 1 ) e^{0x}(3x+1) e0x(3x+1),即对应类型1问题模型中有
(1-1)- λ = 0 \lambda=0 λ=0;
- P m ( x ) P_m(x) Pm(x)是一次多项式 3 x + 1 3x+1 3x+1
- m = 1 m=1 m=1
- 令 f ( x ) f(x) f(x)= 3 x + 1 3x+1 3x+1= e 0 x ( 3 x + 1 ) e^{0x}(3x+1) e0x(3x+1),即对应类型1问题模型中有
- 特征方程为 r 2 − 2 r − 3 = 0 r^2-2r-3=0 r2−2r−3=0
(2) - 检查 λ \lambda λ和(2)的根的关系: λ = 0 \lambda=0 λ=0不是(2)的根,
- 应用类型1的待定系数法结论可知,方程(1)的特解可以设为 y ∗ y^* y∗= x k Q m ( x ) e λ x x^kQ_{m}(x)e^{\lambda{x}} xkQm(x)eλx,代入(1-1),可以具体为 y ∗ y^* y∗= Q 1 ( x ) Q_{1}(x) Q1(x)= b 0 x + b 1 b_0{x}+b_1 b0x+b1
(3)( Q 1 ( x ) Q_1(x) Q1(x)是一次多项式) - 将(3)代入到方程(1): − 2 b 0 − 3 ( b 0 x + b 1 ) -2b_0-3(b_0{x}+b_1) −2b0−3(b0x+b1)= 3 x + 1 3x+1 3x+1,整理得 − 3 b 0 x − 2 b 0 − 3 b 1 -3b_0x-2b_0-3b_1 −3b0x−2b0−3b1= 3 x − 1 3x-1 3x−1
(4) - 由系数比较法, − 3 b 0 = 3 -3b_0=3 −3b0=3; − 2 b 0 − 3 b 1 -2b_0-3b_1 −2b0−3b1= 1 1 1,解得 b 0 = − 1 b_0=-1 b0=−1; b 1 = 1 3 b_1=\frac{1}{3} b1=31,从而得到特解为 y ∗ = − x + 1 3 y^*=-x+\frac{1}{3} y∗=−x+31
- 方程类型分析:方程(1)是常系数非齐次线性微分方程中的经典类型1
相关文章:

AM@二阶常系数非齐次线性微分方程@待定系数法可解决的经典类型1
文章目录 abstract二阶常系数非齐次线性微分方程待定系数法可解类型类型1小结例 abstract 二阶常系数非齐次线性微分方程待定系数法可解决的经典类型1及其解法总结与应用 本文给出类型1为什么可以通过待定求出特解,并且待定函数要设成什么形式推理过程有一定工作量,而在应用中…...

大数据技术笔记
1. 大数据技术简介 大数据技术是一系列的工具和方法,它们可以帮助我们收集、存储和分析大量的数据,并将结果呈现给我们。 2. 大数据计算模式 我们需要一些方法来处理这些数据,就像我们需要各种各样的厨具来处理食材一样。这些方法被称为大…...

Vue 3 中的 Composition API
✨理解 Vue 3 中的 Composition API 🎃 Vue 3 引入了全新的 Composition API,相较于传统的 Options API,它具备许多优势和适用场景。下面将介绍 Composition API 的优势和使用场景,并为你带来更好的开发体验。 🎁 Co…...

《TCP/IP详解 卷一:协议》第5章的IPv4数据报的总长度字段出现“不需要大于576字节的IPv4数据报“相关内容的解释
《TCP/IP详解 卷一:协议》第5章的IPv4数据报的总长度字段的一些解释,出现以下内容(有省略): ....另外,主机不需要接收大于576字节的IPv4数据报.....以避免576字节的IPv4限制。 英文原文的内容(有…...

PO-java客户端连接错误can not connect to server
问题描述: 换电脑或者网络环境改变了,PO下载EST ID的jnlp提示can not connect to server*** ;**message server***这类错误 原因分析: 基本上都是PO消息服务器连接不上导致的错误,原理有均衡负载对应的IP转接后端口不…...

PM2 vs Kubernetes:在部署 Node.js 服务时使用哪个?
Node.js 已成为 Web 开发中的热门技术之一,但如果我们想成功地将 Node.js 应用程序交付给用户,我们需要考虑部署和管理这些应用程序。两个常见的选项是 PM2 和 Kubernetes。PM2 是一个用于运行和管理 Node.js 应用程序的进程管理器,它能够创建…...
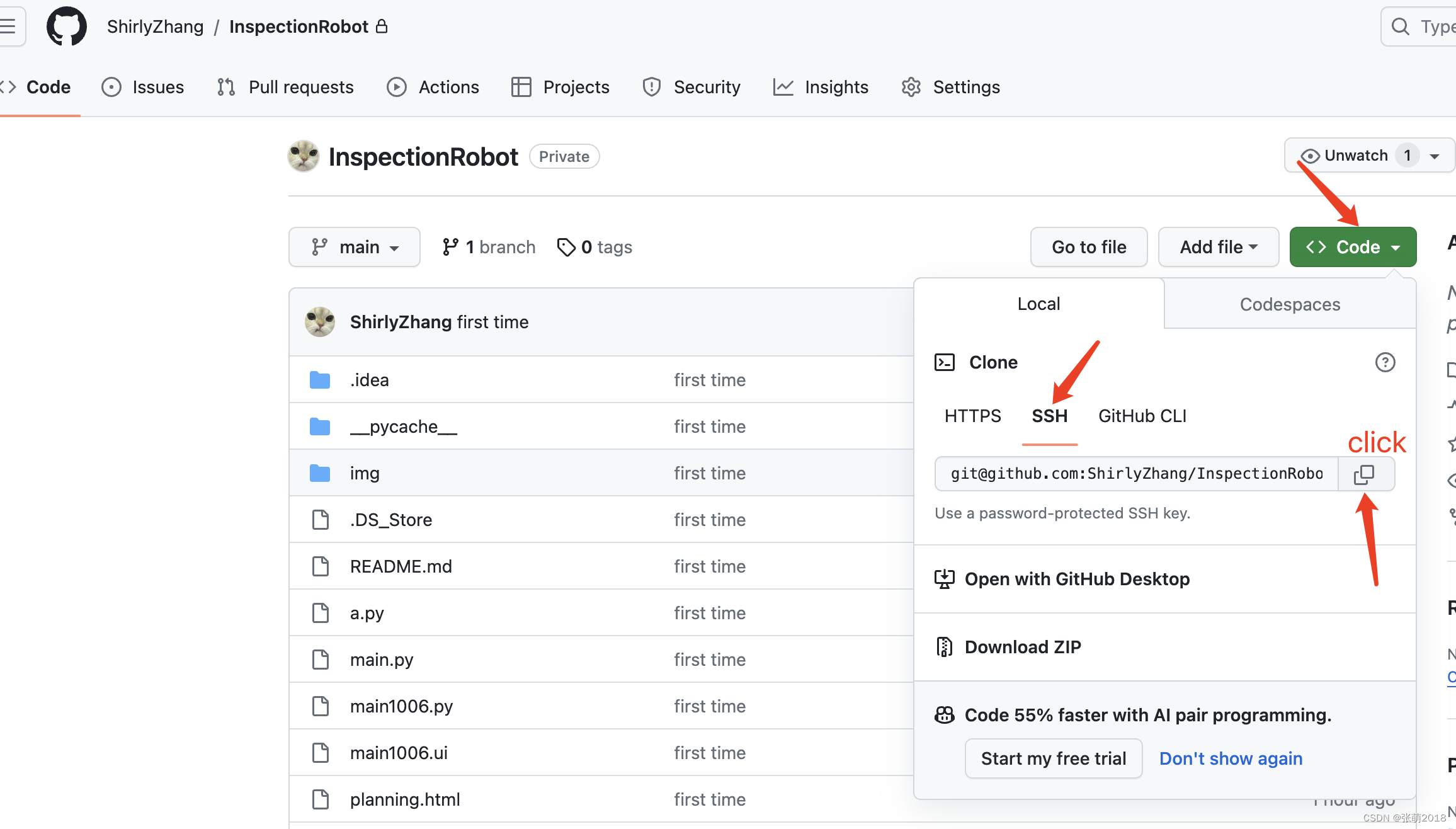
配置git并把本地项目连接github
一.配置git 1.下载git(Git),但推荐使用国内镜像下载(CNPM Binaries Mirror) 选好64和版本号下载,全部点下一步 下载完成后打开终端,输入 git --version 出现版本号则说明安装成功 然后继续…...
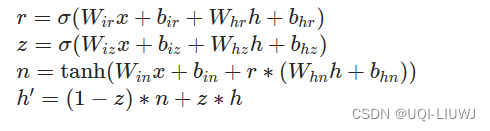
pytorch笔记 GRUCELL
1 介绍 GRU的一个单元 2 基本使用方法 torch.nn.GRUCell(input_size, hidden_size, biasTrue, deviceNone, dtypeNone) 输入:(batch,input_size) 输出和隐藏层:(batch,hidden_size…...

不解压,也能列出文件信息
gz文件,不解压,查看压缩前文件的大小: gzip -l ~$ ll -rw-r--r-- 1 fee fee 17343450 Nov 2 12:02 xxx.log.2023-11-02T04-02-56.000.1 -rw-r--r-- 1 fee fee 3150599 Nov 2 12:02 xxx.log.2023-11-02T04-02-56.000.1.gz ~$ gzip -l gb…...
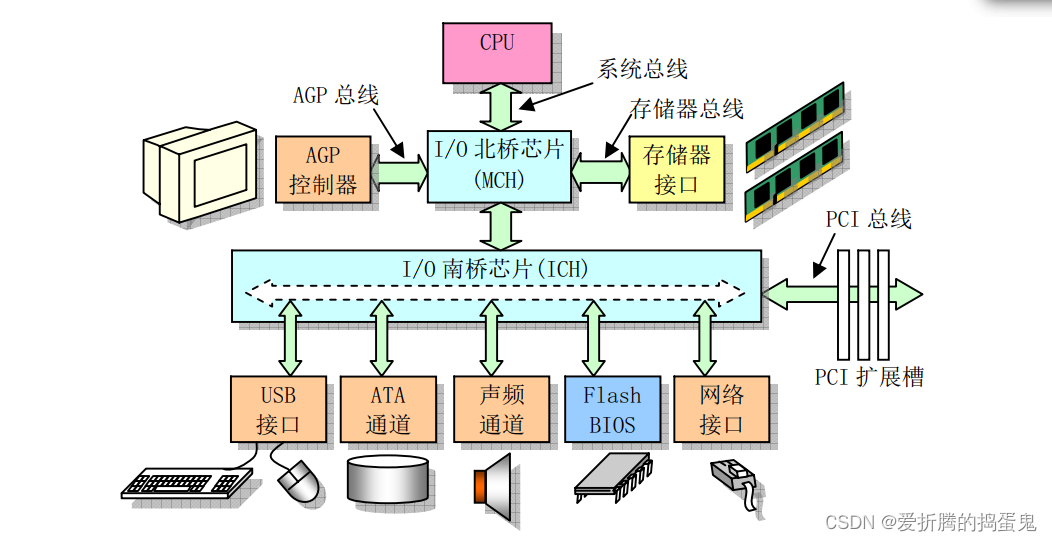
微型计算机组成原理
1、微型计算机组成 一个传统微型计算机硬件组成如下图 CPU通过地址线、数据线和控制信号线组成的本地总线(内部总线)与系统其他部分进行数据通信。 地址线用于提供内存或I/O设备的地址,即指明需要读/写数据的具体位置;数据线用…...
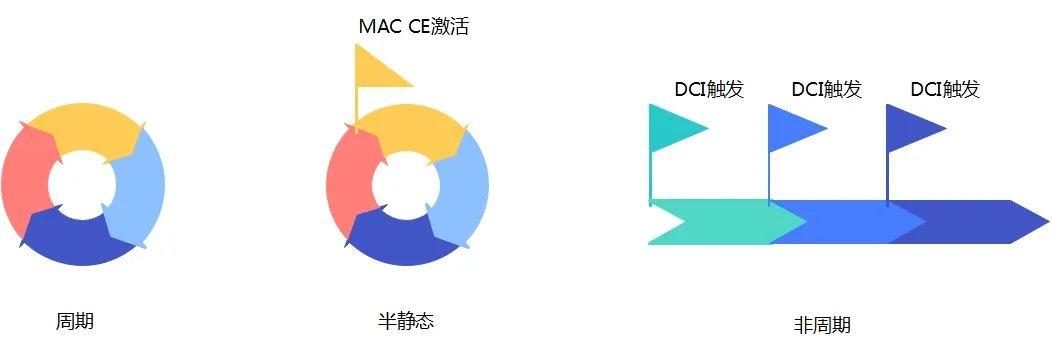
基站/手机是怎么知道信道情况的?
在无线通信系统中,信道的情况对信号的发送起到至关重要的作用,基站和手机根据信道的情况选择合适的资源配置和发送方式进行通信,那么基站或者手机是怎么知道信道的情况呢? 我们先来看生活中的一个例子,从A地发货到B地…...

进程/线程
进程是资源单位, 线程是执行单位。 每一个进程至少要有一个线程,启动每一个程序默认都会有一个主线程 1.多线程的两种实现 from threading import Thread#方法一 def func(name):for i in range(10):print(name, i)if __name__ __main__:t Thread(targetfunc, …...
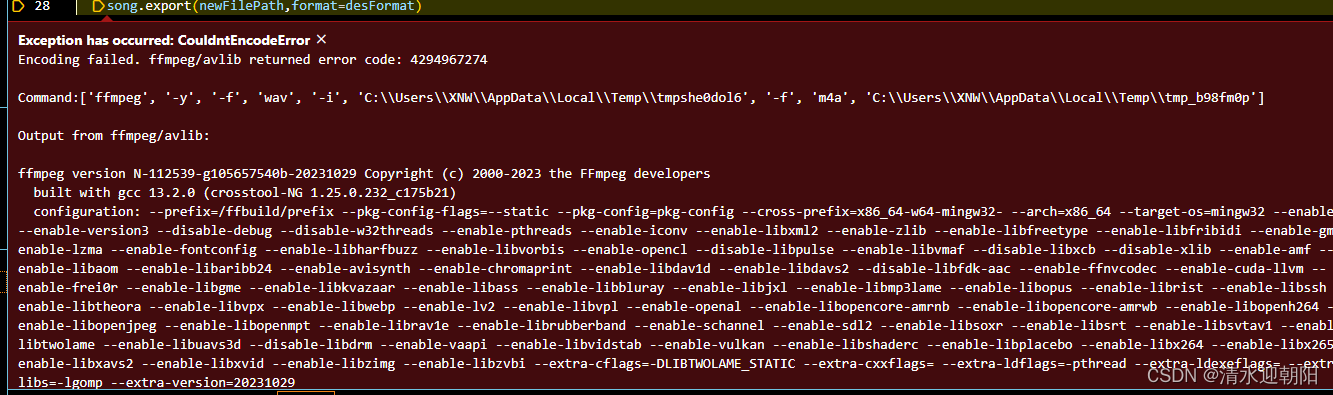
Python 应用 之 转换音频格式
目录 一、python音频转换 1、pydub 音频包安装 2、 ffmpeg安装 1)、解压后,添加到环境变量中 2)、可以直接放在python安装目录下 3、python程序 1)、引入相关包 2)、重命名 3)、to Mp3 4…...

Oracle JDK 和OpenJDK两者有什么异同点
Oracle JDK 和 OpenJDK 是两种不同版本的 Java Development Kit(Java 开发工具包),它们都提供了用于开发 Java 程序的一系列工具和库。以下是它们之间的一些主要异同点: 相同点: 功能:在大多数情况下&…...
GPT引发智能AI时代潮流
最近GPT概念爆火,许多行业开始竞相发展AI ,工作就业也将面临跳转,目前测试就业形势就分为了两大类,一类是测试行业如功能、性能、自动化综合性人才就业技能需求,另一类便是AI测试行业的需求普遍增长,原本由…...

FreeSWITCH mrcp-v2小记
最近得知有人受mrcp的困扰,于是写了这篇小文,希望能有所帮助 FreeSWITCH版本选择 目前当然选择1.10.10,不建议老版本,差别在于老版本用到的libmrcp比较旧,是1.2版本,bug比较多,有时会crash&am…...
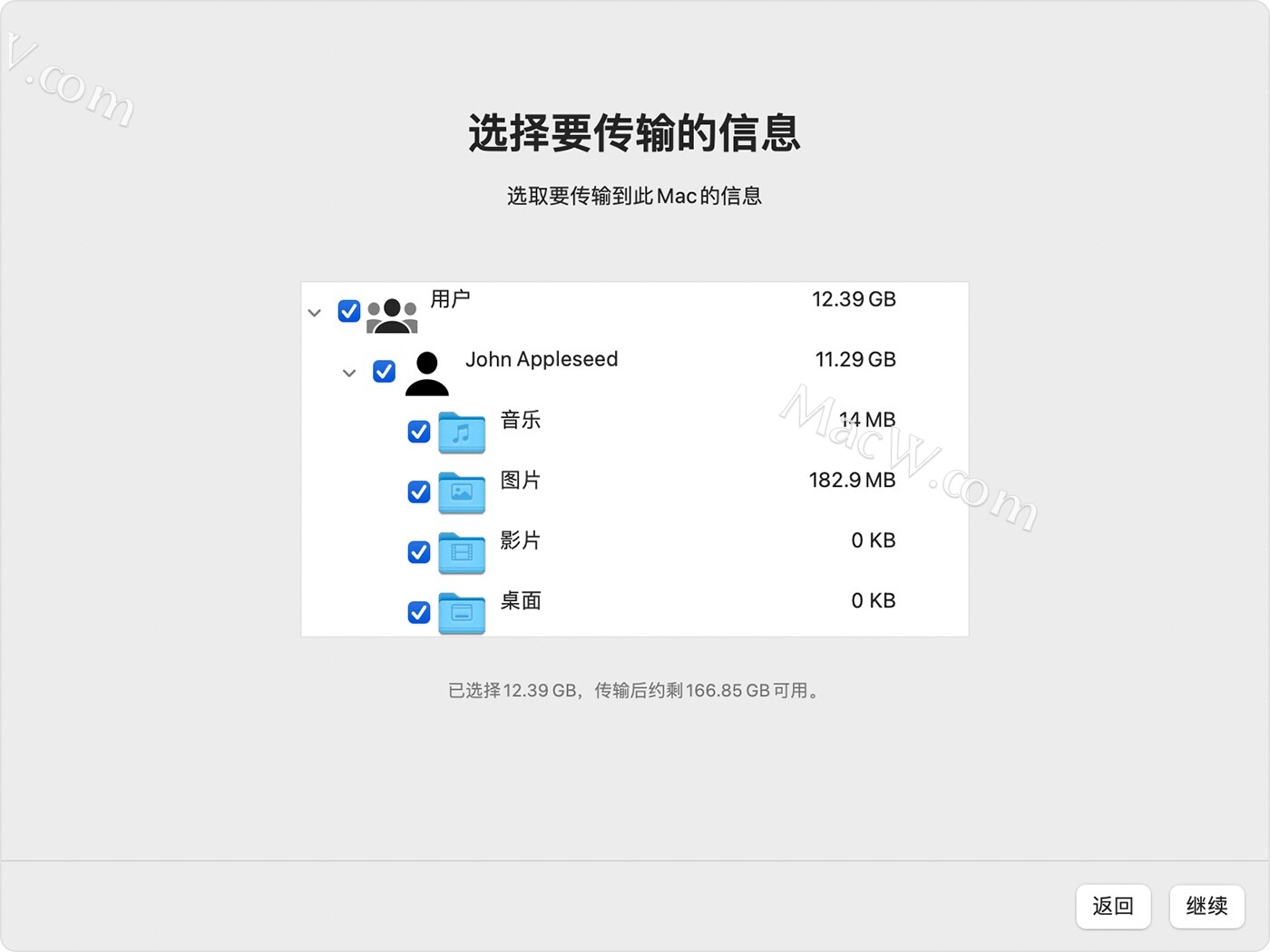
如何将你的PC电脑数据迁移到Mac电脑?使用“迁移助理”从 PC 传输到 Mac的具体操作教程
有的小伙伴因为某一项工作或者其它原因由Windows电脑换成了Mac电脑,但是数据和文件都在原先的Windows电脑上,不知道怎么传输。接下来小编就为大家介绍使用“迁移助理”将你的通讯录、日历、电子邮件帐户等内容从 Windows PC 传输到 Mac 上的相应位置。 在…...

Elasticsearch集群搭建、数据分片以及位置坐标实现附近的人搜索
集群搭建、数据分片 es使用两种不同的方式来发现对方: 广播单播也可以同时使用两者,但默认的广播,单播需要已知节点列表来完成 一 广播方式 当es实例启动的时候,它发送了广播的ping请求到地址224.2.2.4:54328。而其他的es实例使用同样的集群名称响应了这个请求。 一般这…...

深度学习_3 数据操作之线代,微分
线代基础 标量 只有一个元素的张量。可以通过 x torch.tensor(3.0) 方式创建。 向量 由多个标量组成的列表(一维张量)。比如 x torch.arange(4) 就是创建了一个1*4的向量。可以通过下标获取特定元素(x[3]),可以通…...
树莓派安装Ubuntu22.04LTS桌面版
工具:树莓派4B Raspberry Pi 自己下载的ubuntu22.04LTS img磁盘镜像文件 这里有一个小技巧:这个Raspberry Pi的选择镜像的时候在最后面一行可以选择自定义的镜像,哈哈哈哈,这就使得我们可以自己下载,而且知道那个文…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
