当前位置： 首页 > news >正文

PCL 计算一个平面与一个三角形的交线

news 2026/2/11 3:29:36

文章目录

  • 一、简介
  • 二、实现代码
  • 三、实现效果
  • 参考资料

一、简介

这里实现一个很有趣的功能，就是获取一个平面与一个三角形的交线，具体的思路很简单，就是借助之前的博客中的思路：Matlab 计算一个平面与一条线段的交点，我们只需要遍历三角形中的所有边即可获取我们想要的交线，这里是PCL版本。

二、实现代码


//标准文件
#include <iostream>
#include <thread>

相关文章：

PCL 计算一个平面与一个三角形的交线

文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 这里实现一个很有趣的功能，就是获取一个平面与一个三角形的交线，具体的思路很简单，就是借助之前的博客中的思路：Matlab 计算一个平面与一条线段的交点，我们只需要遍历三角形中的所有边即可获取我们想要的交线，…...

编程日记 2023/11/3 2:34:59

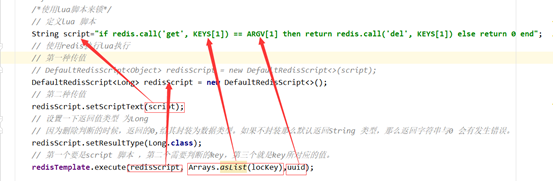
Redis 应用问题

1-缓存穿透 1.1-问题描述 Key 对应的数据在数据源并不存在&#xff0c;每次针对此 Key 的请求从缓存获取不到&#xff0c;请求都会压到数据源&#xff0c;从而可能压垮数据源。 比如&#xff1a;用一个不存在的用户ID 获取用户信息&#xff0c;不论缓存还是数据库都没有&…...

编程日记 2023/11/3 2:33:57

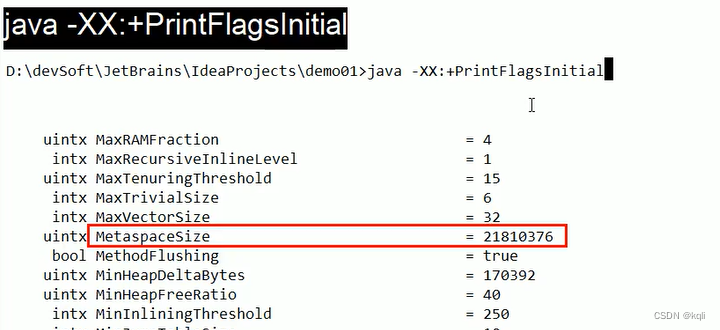
Java 谈谈你对OOM的认识

文章目录 前言一、基础架构二、常见OOM1、栈内存溢出java.lang.StackOverflowError2、堆内存溢出java.lang.OutOfMemoryError&#xff1a;Java heap space3、GC回收时间过长java.lang.OutOfMemoryError: GC overhead limit exceeded4、NIO程序堆外内存溢出java.lang.OutOfMemor…...

编程日记 2023/11/3 2:32:55

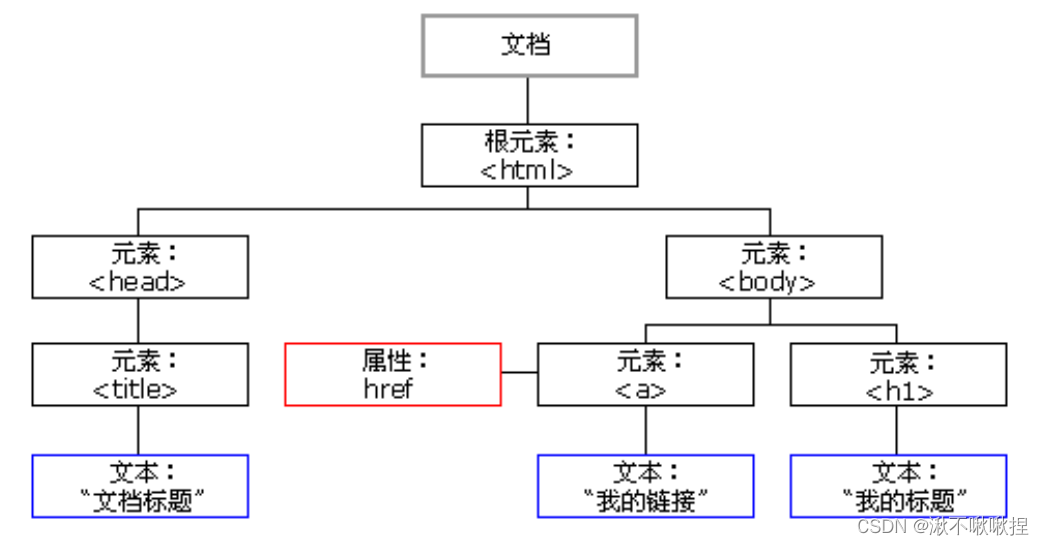
JavaScript中BOM与DOM

BOM window对象 所有的浏览器都支持window对象&#xff0c;他表示浏览器窗口&#xff0c; 所有 JavaScript 全局对象、函数以及变量均自动成为 window 对象的成员。 全局变量是 window 对象的属性。全局函数是 window 对象的方法。 接下来要讲的HTML DOM 的 document 也是…...

编程日记 2023/11/3 2:31:54

Nginx域名重定向（如何访问的域名和实际的数据请求路径不同，可解决前端跨域）

感情需要被抑制&#xff0c;不能泛滥… 当需要将一个域名重定向到另一个域名并且用户仍然看到原始域名时&#xff0c;Nginx是一个强大的工具。这种场景通常涉及到反向代理或重写URL的技巧。在本篇博客中&#xff0c;我们将详细介绍如何使用Nginx来实现这个目标&#xff0c;以及…...

编程日记 2023/11/3 2:30:52

2023年11月2日历史上的今天大事件早读

1082年11月02日宋徽宗出生 1861年11月02日辛酉政变 1910年11月02日中国社会学家和人类学家费孝通诞生 1910年11月02日畜生态学科的创始人汤逸人诞生 1917年11月02日《贝尔福宣言》和犹太复国主义 1917年11月02日美日订立“兰辛—石井协定”损害中国利益 1937年11月02日忻…...

编程日记 2023/11/3 2:29:50

红帽Redhat--Ansible实战1

在运行Windows操作系统的主机LAPTOP-OUR52V78上安装有VMware Workstation Player软件。因为Windows自带的虚拟机平台软件"Hyper-V"使用难度较大&#xff0c;而且关于在"Hyper-V"上运行虚拟机&#xff0c;修改虚拟机错误的相关技术博客和文章的数量稀少&…...

编程日记 2023/11/3 2:27:48

213. 打家劫舍 II

你是一个专业的小偷&#xff0c;计划偷窃沿街的房屋&#xff0c;每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 &#xff0c;这意味着第一个房屋和最后一个房屋是紧挨着的。同时&#xff0c;相邻的房屋装有相互连通的防盗系统&#xff0c;如果两间相邻的房屋在同一…...

编程日记 2023/11/3 2:25:46

Spring 与 Spring Boot

什么是 Spring 可以理解 Spring 是一个框架。这个框架最早来源于在差不多的 20 年前的 2002 年。 在那个时候 Java 世界的开发还是以 EJB 为主&#xff0c;因为在这之前的大部分应用都会使用服务器客户端的应用模式。 其实这个模式在现在还是在使用的&#xff0c;例如 IBM 系统…...

编程日记 2023/11/3 2:24:45

Flutter 04 按钮Button和事件处理、弹框Dialog、Toast

一、按钮组件 1、按钮类型&#xff1a; 2、按钮实现效果&#xff1a; import package:flutter/material.dart;void main() {runApp(const MyApp()); }class MyApp extends StatelessWidget {const MyApp({Key? key}) : super(key: key);overrideWidget build(BuildContext co…...

编程日记 2023/11/3 2:23:43

thinkphp6多用用模式下缩短路由隐藏index应用名

thinkphp6多用用模式下缩短路由隐藏index应用名方法&#xff1a; 找到入口文件&#xff0c;一般public目录下index.php 找到 $response $http->run(); 替换为如下代码即可 // 关键在此处 $_amain index; $_aother admin|common; // 匹配此条件&#xff0c;就按照tp默…...

编程日记 2023/11/3 2:21:37

AM@二阶常系数非齐次线性微分方程@待定系数法可解决的经典类型1

文章目录 abstract二阶常系数非齐次线性微分方程待定系数法可解类型类型1小结例 abstract 二阶常系数非齐次线性微分方程待定系数法可解决的经典类型1及其解法总结与应用 本文给出类型1为什么可以通过待定求出特解,并且待定函数要设成什么形式推理过程有一定工作量,而在应用中…...

编程日记 2023/11/3 2:19:35

大数据技术笔记

1. 大数据技术简介 大数据技术是一系列的工具和方法&#xff0c;它们可以帮助我们收集、存储和分析大量的数据&#xff0c;并将结果呈现给我们。 2. 大数据计算模式 我们需要一些方法来处理这些数据&#xff0c;就像我们需要各种各样的厨具来处理食材一样。这些方法被称为大…...

编程日记 2023/11/3 2:17:32

Vue 3 中的 Composition API

✨理解 Vue 3 中的 Composition API &#x1f383; Vue 3 引入了全新的 Composition API&#xff0c;相较于传统的 Options API&#xff0c;它具备许多优势和适用场景。下面将介绍 Composition API 的优势和使用场景&#xff0c;并为你带来更好的开发体验。 &#x1f381; Co…...

编程日记 2023/11/3 2:15:29

《TCP/IP详解 卷一：协议》第5章的IPv4数据报的总长度字段出现“不需要大于576字节的IPv4数据报“相关内容的解释

《TCP/IP详解 卷一&#xff1a;协议》第5章的IPv4数据报的总长度字段的一些解释&#xff0c;出现以下内容&#xff08;有省略&#xff09;&#xff1a; ....另外&#xff0c;主机不需要接收大于576字节的IPv4数据报.....以避免576字节的IPv4限制。 英文原文的内容&#xff08;有…...

编程日记 2023/11/3 2:14:28

PO-java客户端连接错误can not connect to server

问题描述&#xff1a; 换电脑或者网络环境改变了&#xff0c;PO下载EST ID的jnlp提示can not connect to server*** &#xff1b;**message server***这类错误 原因分析&#xff1a; 基本上都是PO消息服务器连接不上导致的错误&#xff0c;原理有均衡负载对应的IP转接后端口不…...

编程日记 2023/11/3 2:13:27

PM2 vs Kubernetes：在部署 Node.js 服务时使用哪个？

Node.js 已成为 Web 开发中的热门技术之一&#xff0c;但如果我们想成功地将 Node.js 应用程序交付给用户&#xff0c;我们需要考虑部署和管理这些应用程序。两个常见的选项是 PM2 和 Kubernetes。PM2 是一个用于运行和管理 Node.js 应用程序的进程管理器&#xff0c;它能够创建…...

编程日记 2023/11/3 2:12:26

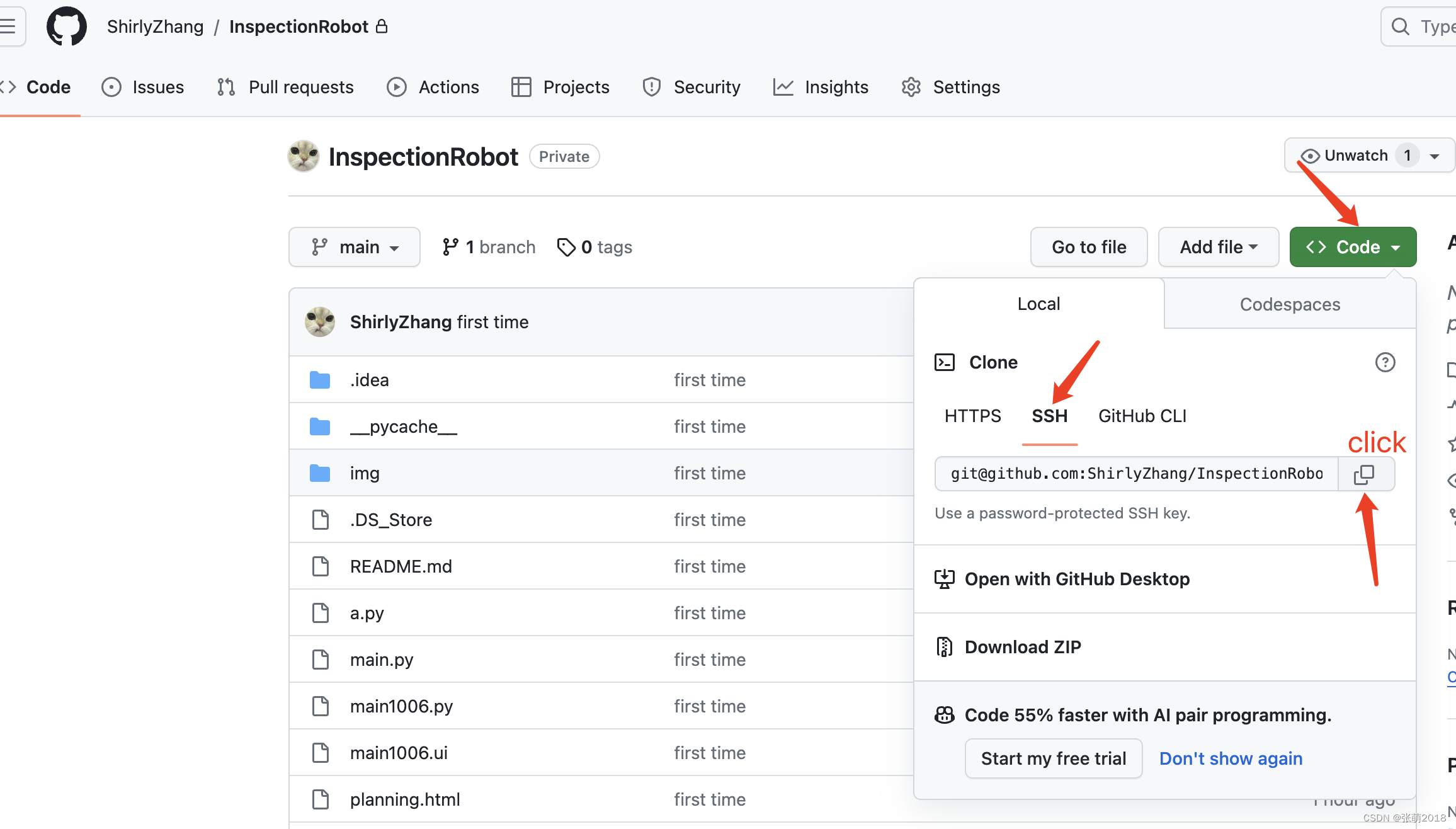
配置git并把本地项目连接github

一.配置git 1.下载git&#xff08;Git&#xff09;&#xff0c;但推荐使用国内镜像下载&#xff08;CNPM Binaries Mirror&#xff09; 选好64和版本号下载&#xff0c;全部点下一步 下载完成后打开终端&#xff0c;输入 git --version 出现版本号则说明安装成功 然后继续…...

编程日记 2023/11/3 2:10:23

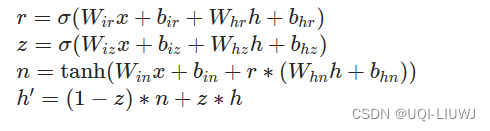
pytorch笔记 GRUCELL

1 介绍 GRU的一个单元 2 基本使用方法 torch.nn.GRUCell(input_size, hidden_size, biasTrue, deviceNone, dtypeNone) 输入&#xff1a;&#xff08;batch&#xff0c;input_size&#xff09; 输出和隐藏层&#xff1a;&#xff08;batch&#xff0c;hidden_size&#xf…...

编程日记 2023/11/3 2:09:23

不解压，也能列出文件信息

gz文件&#xff0c;不解压&#xff0c;查看压缩前文件的大小&#xff1a; gzip -l ~$ ll -rw-r--r-- 1 fee fee 17343450 Nov 2 12:02 xxx.log.2023-11-02T04-02-56.000.1 -rw-r--r-- 1 fee fee 3150599 Nov 2 12:02 xxx.log.2023-11-02T04-02-56.000.1.gz ~$ gzip -l gb…...

编程日记 2023/11/3 2:06:18

Ubuntu系统下交叉编译openssl

一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机&#xff1a;Ubuntu 20.04.6 LTSHost&#xff1a;ARM32位交叉编译器&#xff1a;arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

编程新知 2025/11/10 15:33:04

在Ubuntu中设置开机自动运行（sudo）指令的指南

在Ubuntu系统中&#xff0c;有时需要在系统启动时自动执行某些命令&#xff0c;特别是需要 sudo权限的指令。为了实现这一功能&#xff0c;可以使用多种方法&#xff0c;包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法&#xff0c;并提供…...

编程新知 2025/12/23 11:20:24

什么？连接服务器也能可视化显示界面？：基于X11 Forwarding + CentOS + MobaXterm实战指南

文章目录 什么是X11？环境准备实战步骤1️⃣ 服务器端配置（CentOS）2️⃣ 客户端配置（MobaXterm）3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/55aefaea8a9f477e86d065227851fe3d.pn…...

编程新知 2025/10/2 17:12:14

RNN避坑指南：从数学推导到LSTM/GRU工业级部署实战流程

本文较长&#xff0c;建议点赞收藏&#xff0c;以免遗失。更多AI大模型应用开发学习视频及资料&#xff0c;尽在聚客AI学院。 本文全面剖析RNN核心原理&#xff0c;深入讲解梯度消失/爆炸问题&#xff0c;并通过LSTM/GRU结构实现解决方案&#xff0c;提供时间序列预测和文本生成…...

编程新知 2026/1/20 17:16:46

dify打造数据可视化图表

一、概述 在日常工作和学习中&#xff0c;我们经常需要和数据打交道。无论是分析报告、项目展示&#xff0c;还是简单的数据洞察&#xff0c;一个清晰直观的图表&#xff0c;往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server&#xff0c;由蚂蚁集团 AntV 团队…...

编程新知 2026/1/20 20:10:03

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中&#xff0c;新增了一个本地验证码接口 /code&#xff0c;使用函数式路由&#xff08;RouterFunction&#xff09;和 Hutool 的 Circle…...

编程新知 2026/2/10 20:18:09

C++.OpenGL （20/64）混合（Blending）

混合（Blending） 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

编程新知 2026/1/20 5:33:17

如何应对敏捷转型中的团队阻力

应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中&#xff0c;明确沟通敏捷转型目的尤为关键&#xff0c;团队成员只有清晰理解转型背后的原因和利益&#xff0c;才能降低对变化的…...

编程新知 2026/2/4 16:04:15

SpringAI实战：ChatModel智能对话全解

一、引言&#xff1a;Spring AI 与 Chat Model 的核心价值 &#x1f680; 在 Java 生态中集成大模型能力&#xff0c;Spring AI 提供了高效的解决方案 &#x1f916;。其中 Chat Model 作为核心交互组件&#xff0c;通过标准化接口简化了与大语言模型&#xff08;LLM&#xff0…...

编程新知 2025/9/27 0:41:04

【Veristand】Veristand环境安装教程-Linux RT / Windows

首先声明&#xff0c;此教程是针对Simulink编译模型并导入Veristand中编写的&#xff0c;同时需要注意的是老用户编译可能用的是Veristand Model Framework&#xff0c;那个是历史版本&#xff0c;且NI不会再维护&#xff0c;新版本编译支持为VeriStand Model Generation Suppo…...

编程新知 2026/2/5 20:04:55