约数之和 (普通快速幂求逆元做法)
假设现在有两个自然数 A 和 B,S 是 AB
的所有约数之和。
请你求出 Smod9901
的值是多少。
输入格式
在一行中输入用空格隔开的两个整数 A
和 B
。
输出格式
输出一个整数,代表 Smod9901
的值。
数据范围
0≤A,B≤5×107
输入样例:
2 3
输出样例:
15
注意: A
和 B 不会同时为 0。
思路
因为要求p^0+p^1+...+p^k-1,所以这是一个等比数列,完全可以用快速幂求逆元然后用等比数列求和公式得到答案

#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
#include<unordered_map>
#include<map>
#include<bitset>
#include<cstring>
#include <unordered_set>
//#include<priority_queue>
#include<queue>
#include<deque>
#include<set>
#include<stdlib.h>
#define dbug cout<<"*****hear*****"<<endl;
#define rep(a,b,c) for(ll a=b;a<=c;a++)
#define per(a,b,c) for(ll a=b;a>=c;a--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
#define endl "\n"//交互题一定要关!!!!!!!!!
#define lowbit(x) (x&-x)
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//priority_queue<int,vector<int>,greater<int> >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> PII;
typedef pair<long double,long double> PDD;ll INF = 0x3f3f3f3f;
//const ll LINF=LLONG_MAX;
// int get_len(int x1,int y1,int x2,int y2)
// {
// return (x2-x1)*(x2-x1) + (y2-y1)*(y2-y1);
// }
const ll N = 2e5+ 10;const ll mod1 =998244353;const ll mod2 =1e9+7;
// const ll hash_num = 3e9+9;
ll n,m,ca;
ll arr[N],brr[N],crr[N],drr[N];
//ll h[N],ne[N],e[N],w[N],book[N],idx;
//ll idx;// void add(ll a, ll b , ll c)
// {
// e[idx] = b, w[idx] = c,ne[idx] = h[a], h[a] =idx ++ ;
// }
ll mod=9901;
unordered_map<ll,ll>prime;ll fast_power(ll a,ll b)//快速幂
{ll res=1;while(b){if(b&1)res=res*a%mod;b >>= 1;a=a*a%mod;}return res;
}void get(ll x)//获得质因数
{for(ll i=2;i<=x/i;i++){while(x%i==0){x/=i;prime[i]++;}}if(x>1)prime[x]++;
}ll sum(ll p,ll k)//sum函数
{if(k==1)return 1;if(k%2==0){return (1+fast_power(p,k/2))*sum(p,k/2)%mod;}else{return (fast_power(p, k - 1) + sum(p, k - 1)) % mod;}
}void solve()
{cin >> n >> m;get(n);ll ans=1;for(auto it : prime){ll a = it.first, b = it.second * m;if((a-1)%mod==0)//如果a-1是mod的倍数的话那么其实就是k+1个1相加{ans=ans*(b+1)%mod;}else{ans=ans*(fast_power(a,b+1)-1)%mod*(fast_power(a-1,mod-2))%mod;//这里是将求和公式上下都提取一个负号变成了(a^b+1)-1和a-1}}if(!n)ans=0;cout << (ans%mod+mod)%mod;
}int main()
{IOS;ll _;_=1;//scanf("%lld",&_);// cin>>_;ca=1;while(_--){solve(); ca++;} return 0;
}
相关文章:

约数之和 (普通快速幂求逆元做法)
假设现在有两个自然数 A 和 B,S 是 AB 的所有约数之和。 请你求出 Smod9901 的值是多少。 输入格式 在一行中输入用空格隔开的两个整数 A 和 B 。 输出格式 输出一个整数,代表 Smod9901 的值。 数据范围 0≤A,B≤5107 输入样例: …...

每日一题(LeetCode)----二分查找(三)
每日一题(LeetCode)----二分查找(三) 1.题目(69. x 的平方根 ) 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 **注意…...

使用 TensorFlow FasterRCNN 网络进行目标检测
目录 描述 此示例的工作原理 处理输入图形 数据准备 sampleUffFasterRCNN 插件 验证输出 TensorRT API 层和操作 TensorRT API 层和操作 先决条件 运行示例 示例 --help 选项 附加资源 许可 变更记录 已知问题 本示例,sampleUffFasterRCNN࿰…...

数据结构——顺序表(SeqList)
目录 1. 顺序表介绍 2. 顺序表工程 2.1 顺序表定义 2.1.1 静态顺序表 2.1.2 动态顺序表 2.2顺序表接口 2.2.1 顺序表初始化 2.2.2 顺序表打印 2.2.3 顺序表销毁 2.2.4 顺序表数据插入 2.2.4.1 容量检查 2.2.4.2 顺序表尾插 2.2.4.3 顺序表头插 2.2.4.4 顺序表随机…...

Uni-App 快捷登录
uniapp 实现一键登录前置条件: 开通uniCloud, 开通一键登录功能参考的文档 : 官网 - 一键登录uniapp指南 : https://uniapp.dcloud.net.cn/univerify.html#%E6%A6%82%E8%BF%B0 官网 - 一键登录开通指南 : https://ask.dcloud.net.cn/article/37965 官网 - unicloud使用指南 htt…...

DbUtils + Druid 实现 JDBC 操作 --- 附BaseDao
文章目录 Apache-DBUtils实现CRUD操作1 Apache-DBUtils简介2 主要API的使用2.1 DbUtils2.2 QueryRunner类2.3 ResultSetHandler接口及实现类 3 JDBCUtil 工具类编写3.1 导包3.2 编写配置文件3.3 编写代码 4 BaseDao 编写 Apache-DBUtils实现CRUD操作 1 Apache-DBUtils简介 com…...

css:元素居中整理水平居中、垂直居中、水平垂直居中
目录 1、水平居中1.1、行内元素1.2、块级元素 2、垂直居中2.1、单行文字2.2、多行文字2.3、图片垂直居中 3、水平垂直居中参考文章 1、水平居中 1.1、行内元素 行内元素(比如文字,span,图片等)的水平居中,其父元素中…...

从零开始的目标检测和关键点检测(二):训练一个Glue的RTMDet模型
从零开始的目标检测和关键点检测(二):训练一个Glue的RTMDet模型 一、config文件解读二、开始训练三、数据集分析四、ncnn部署 从零开始的目标检测和关键点检测(一):用labelme标注数据集 从零开始的目标检测…...

React18新特性?
文章目录 前言Automatic BatchingTransitionsSuspenseNew Hooks后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:react.js 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。…...
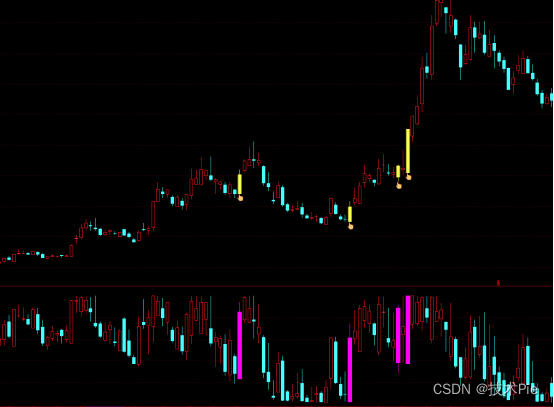
筹码博弈K线长阳选股公式,穿越筹码密集区
普通K线是由最高价、开盘价、最低价、收盘价四个价格构成的,而博弈K线是以这个四个价格对应的获利盘构成K线,反映筹码的获利情况。把鼠标移动到K线上,停留在对应的价格,就可以在右侧的筹码分布图看到相应的获利盘数据。࿰…...
)
微服务设计模式-架构真题(六十八)
UNIX的源代码控制工具(Source Code control System,SCCS)是项目开发中常用的()。 源代码静态分析工具文档分析工具版本控制工具再工程工具 答案:C 解析: SCCS是版本控制工具 网闸的描述错误的是()。 双…...

LeetCode----52. N 皇后 II
题目 n 皇后问题 研究的是如何将 n 个皇后放置在 n n 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。 示例 1: 输入:n = 4 输出:2 解释:如上图所示,4 皇后问题存在两个不同的解法。 示例 2: 输入:n = …...
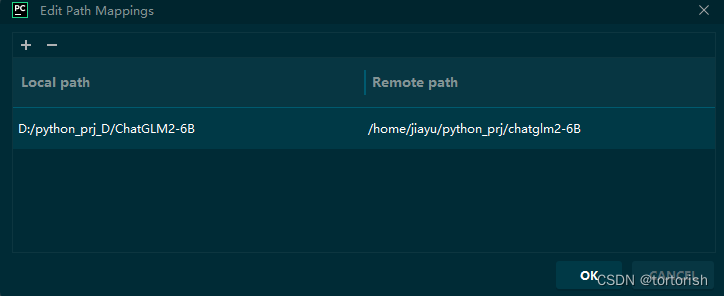
解决pycharm中,远程服务器上文件找不到的问题
一、问题描述 pycharm中,当我们连接到远程服务器上时。编译器中出现报错问题: cant open file /tmp/OV2IRamaar/test.py: [Errno 2] No such file or directory 第二节是原理解释,第三节是解决方法。 二、原理解释 实际上这是由于我们没有设置…...

虹科荣誉 | 喜讯!虹科成功入选“广州首届百家新锐企业”!!
文章来源:虹科品牌部 阅读原文:虹科荣誉 | 喜讯!虹科成功入选“广州首届百家新锐企业”!! 近日,由中共广州市委统战部、广州市工商业联合会、广州市工业和信息化局、广州市人民政府国有资产监督管理委员会…...

如何利用Jmeter从0到1做一次完整的压测?这2个步骤很关键!
压测,在很多项目中都有应用,是测试小伙伴必备的一项基本技能,刚好最近接手了一个小游戏的压测任务,一轮压测下来,颇有收获,赶紧记录下来,与大家分享一下,希望大家能少踩坑。 一、压…...
_2023)
基于STM32+微信小程序设计的智能门锁(4种开锁方式)_2023
一、项目介绍 1.1 项目背景 随着智能家居的普及,智能门锁作为一个非常重要的组成部分,受到了人们越来越多的关注。传统的机械锁门禁已经不能满足人们对于门锁安全、便捷性和智能化的需求,因此市场对于智能门锁的需求不断增加。而随着技术的发展,基于单片机的智能门锁已经…...

享受户外的美好时光:花园吊椅的魅力
拥有舒适的花园吊椅,就像在家中创造了一个度假天堂。这些轻松摇摆的座位为您提供了一个完美的地方,既能舒适躺卧,又能让您在家中的花园或庭院中感受到度假的氛围。度过美好时光的吊椅,将成为家庭花园的一大亮点,为您带…...

游戏中找不到d3dx9_43.dll怎么办,教你快速解决方法
在计算机的世界里,我们经常会遇到一些让人头疼的问题。比如,有一天,小明正在玩他最喜欢的游戏,突然弹出了一个错误提示:“由于找不到d3dx9_43.dll,无法继续执行代码”。小明感到非常困惑,不知道这是什么意思…...

蓝桥杯:买不到的数目
对于两个互质的正整数 n , m n,m n,m,请找出来不能被 n n n和 m m m组成的最大数 X X X 例如:对于4,7那么 X X X17,因为对于大于17的任一数都可由4和7组成。 重新翻译题目: 对于任一大于 X X X的正整数 Y Y Y满足 Y a n b m Y a \times nb \times m …...
Nginx简介,Nginx搭载负载均衡以及Nginx部署前端项目
目录 一. Nginx简介 Nginx的优点 二. Nginx搭载负载均衡 2.1 Nginx安装 2.1.1 安装依赖 2.1.2 解压nginx安装包 2.1.3 安装nginx 2.1.4 启动nginx服务 2.2 tomcat负载均衡 2.3 Nginx配置 三. Nginx前端部署 一. Nginx简介 NGINX(读作:engi…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
