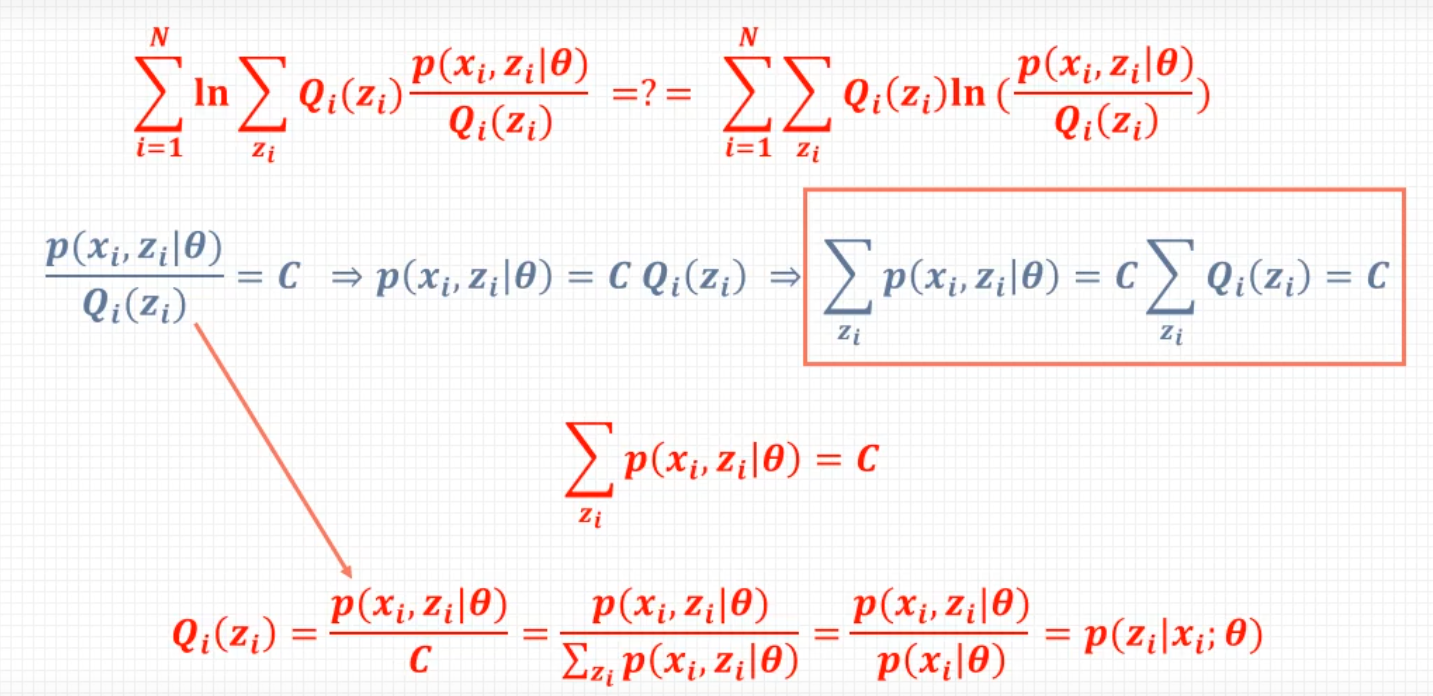第十五章 EM期望极大算法及其推广
文章目录
- 导读
- 符号说明
- 混合模型
- 伯努利混合模型(三硬币模型)
- 问题描述
- 三硬币模型的EM算法
- 1.初值
- 2.E步
- 3.M步
- 初值影响
- p,q 含义
- EM算法另外视角
- Q 函数
- BMM的EM算法
- 目标函数L
- EM算法导出
- 高斯混合模型
- GMM的EM算法
- 1. 明确隐变量, 初值
- 2. E步,确定Q函数
- 3. M步
- 4. 停止条件
- 如何应用
- GMM在聚类中的应用
- Kmeans
- K怎么定
导读
-
概率模型有时既含有观测变量,又含有隐变量或潜在变量。这句很重要,有时候我们能拿到最后的观测结果,却拿不到中间的过程记录
-
EM算法可以用于生成模型的非监督学习,EM算法是个一般方法,不具有具体模型
EM算法是一种迭代算法,用于含有隐变量的概率模型的极大似然估计,或极大后验概率估计
-
似然和概率的关系可以推广了解,这章关于概率和似然的符号表示,概率和似然是同样的形式描述的都是可能性, P ( Y ∣ θ ) P(Y|\theta) P(Y∣θ)是一个两变量的函数,似然是给定结果,求参数可能性;概率是给定参数求结果可能性
是不是可以认为,似然和概率分别对应了Train和Predict的过程?假设给定观测数据Y,其概率分布是P(Y|θ),其中θ是概率分布的参数。那么不完全数据Y的似然函数是通过将Y视为已知观测数据,而将未观测到的数据表示为缺失或隐变量。似然函数可以表示为P(Y|θ)
-
无论是三硬币还是GMM,采样的过程都是如下:
- Sample z i ∼ p ( z ∣ π ) z_i \sim p(z|\pi) zi∼p(z∣π)
- Sample x i ∼ p ( x ∣ π ) x_i \sim p(x|\pi) xi∼p(x∣π)
注意,这里用到了 π \pi π,在强化学习中,随机性策略 π ( x , a ) \pi(x,a) π(x,a)表示为状态 x x x下选择动作 a a a的概率。
-
关于EM算法的解释
注意这里EM不是模型,是个一般方法,不具有具体的模型,这点前面已经提到- PRML
k m e a n s → G M M → E M kmeans \rightarrow GMM \rightarrow EM kmeans→GMM→EM
k均值聚类算法就是一个典型的EM算法 - 统计学习方法
- M L E → B MLE \rightarrow B MLE→B
- F F F函数的极大-极大算法
- PRML
-
HMM作了两个基本假设,实际上是在说在图模型中,存在哪些边
符号说明
一般地,用 Y Y Y表示观测随机变量的数据, Z Z Z表示隐随机变量的数据。 Y Y Y和 Z Z Z一起称为完全数据(complete-data),观测数据 Y Y Y又称为不完全数据(incomplete-data)
上面这个概念很重要,Dempster在1977年提出EM算法的时候文章题目就是《Maximum likelihood from incomplete data via the EM algorithm》,具体看书中本章参考文献[^3]
假设给定观测数据 Y Y Y,其概率分布是 P ( Y ∣ θ ) P(Y|\theta) P(Y∣θ),其中 θ \theta θ是需要估计的模型参数
那么不完全数据 Y Y Y的似然函数是 P ( Y ∣ θ ) P(Y|\theta) P(Y∣θ),对数似然函数是 L ( θ ) = log P ( Y ∣ θ ) L(\theta)=\log P(Y|\theta) L(θ)=logP(Y∣θ)假设 Y Y Y和 Z Z Z的联合概率分布是 P ( Y , Z ∣ θ ) P(Y,Z|\theta) P(Y,Z∣θ),那么完全数据的对数似然函数是 log P ( Y , Z ∣ θ ) \log P(Y,Z|\theta) logP(Y,Z∣θ)
上面这部分简单对应一下,这里说明一下,你看到下面概率分布和似然函数形式看起来一样。在概率中, θ \theta θ已知, 求 Y Y Y,在似然函数中通过已知的Y去求 θ \theta θ
| 观测数据 Y Y Y | 不完全数据 Y Y Y | ||
|---|---|---|---|
| 不完全数据 Y Y Y | 概率分布$P(Y | \theta)$ | 似然函数$P(Y |
| 完全数据 ( Y , Z ) (Y, Z) (Y,Z) | Y Y Y和 Z Z Z的联合概率分布$P(Y,Z | \theta )$ | 似然函数$P(Y,Z |
有一点要注意下, 这里没有出现 X X X, 有提到一种理解
- 有时训练数据只有输入没有对应的输出 ( x 1 , ⋅ ) , ( x 2 , ⋅ ) , … , ( x N , ⋅ ) {(x_1,\cdot),(x_2,\cdot),\dots,(x_N,\cdot)} (x1,⋅),(x2,⋅),…,(xN,⋅),从这样的数据学习模型称为非监督学习问题。
- EM算法可以用于生成模型的非监督学习。
- 生成模型由联合概率分布 P ( X , Y ) P(X,Y) P(X,Y)表示,可以认为非监督学习训练数据是联合概率分布产生的数据。 X X X为观测数据, Y Y Y为未观测数据
有时候,只观测显变量看不到关系,就需要把隐变量引进来。
混合模型
书中用三硬币模型做为引子,在学习这部分内容的时候,注意体会观测数据的作用。
伯努利混合模型(三硬币模型)
问题描述
问题的描述过程中有这样一句:独立的重复 n n n次实验(这里 n = 10 n=10 n=10),观测结果如下:
1,1,0,1,0,0,1,0,1,1
思考上面这个观测和1,1,1,1,1,1,0,0,0,0有区别么?
没有任何信息的前提下,我们得到上面的观测数据可以假定是一个二项分布的形式,参数 n = 10 , p = 0.6 n=10, p=0.6 n=10,p=0.6
把 k = 6 k=6 k=6次成功分布在 n = 10 n=10 n=10次试验中有 C ( 10 , 6 ) C(10,6) C(10,6)种可能
所以上面两个观测序列,可能出自同一个模型。在这个问题的求解上是没有区别的
我们通过一段代码来生成这个数据
import numpy as npp = 0.6
n = 10
# np.random.seed(2018)
flag_a = 1
flag_b = 1
cnt = 0
while flag_a or flag_b:tmp = np.random.binomial(1, p, n)if (tmp == np.array([1,1,1,1,1,1,0,0,0,0])).all():flag_a = 0print("[1,1,1,1,1,1,0,0,0,0] at %d\n" % cnt)if (tmp == np.array([1,1,0,1,0,0,1,0,1,1])).all():flag_b = 0print("[1,1,0,1,0,0,1,0,1,1] at %d\n" % cnt)cnt += 1
实际上题目的描述中说明了观测数据生成的过程,这些参数是未知的,所以需要对这些参数进行估计
三硬币模型可以写作
P ( y ∣ θ ) = ∑ z P ( y , z ∣ θ ) = ∑ z P ( z ∣ θ ) P ( y ∣ z , θ ) = π p y ( 1 − p ) 1 − y + ( 1 − π ) q y ( 1 − q ) 1 − y \begin{equation} \begin{aligned} P(y|\theta)&=\sum_z P(y,z|\theta) \\ &=\sum_z P(z|\theta)P(y|z,\theta) \\ &=\pi p^y (1-p)^{1-y} + (1-\pi)q^y(1-q)^{1-y} \end{aligned} \end{equation} P(y∣θ)=z∑P(y,z∣θ)=z∑P(z∣θ)P(y∣z,θ)=πpy(1−p)1−y+(1−π)qy(1−q)1−y
以上
- 随机变量 y y y是观测变量,表示一次试验观测的结果是1或0
- 随机变量 z z z是隐变量,表示未观测到的掷硬币 A A A的结果
- θ = ( π , p , q ) \theta=(\pi,p,q) θ=(π,p,q)是模型参数
- 这个模型是以上数据(1,1,0,1,0,0,1,0,1,1)的生成模型
观测数据表示为 Y = ( Y 1 , Y 2 , Y 3 , … , Y n ) T Y=(Y_1, Y_2, Y_3, \dots, Y_n)^T Y=(Y1,Y2,Y3,…,Yn)T, 未观测数据表示为 Z = ( Z 1 , Z 2 , Z 3 , … , Z n ) T Z=(Z_1,Z_2, Z_3,\dots, Z_n)^T Z=(Z1,Z2,Z3,…,Zn)T, 则观测数据的似然函数为
其实觉得这里应该是小写的 y = ( y 1 , y 2 , … , y n ) , z = ( z 1 , z 2 , … , z n ) y=(y_1,y_2,\dots,y_n), z=(z_1, z_2, \dots,z_n) y=(y1,y2,…,yn),z=(z1,z2,…,zn)
P ( Y ∣ θ ) = ∑ Z P ( Z ∣ θ ) P ( Y ∣ Z , θ ) P(Y|\theta) = \sum\limits_{Z}P(Z|\theta)P(Y|Z,\theta) P(Y∣θ)=Z∑P(Z∣θ)P(Y∣Z,θ)
注意这里的求和是下面的"+"描述的部分
即
P ( Y ∣ θ ) = ∏ j = 1 n [ π p y j ( 1 − p ) 1 − y j + ( 1 − π ) q y j ( 1 − q ) 1 − y j ] P(Y|\theta)=\prod\limits^{n}_{j=1}[\pi p^{y_j}(1-p)^{1-y_j}+(1-\pi)q^{y_j}(1-q)^{1-y_j}] P(Y∣θ)=j=1∏n[πpyj(1−p)1−yj+(1−π)qyj(1−q)1−yj]
p ( x ∣ θ ) p ( θ ) = p ( θ ∣ x ) p ( x ) ⇒ p ( θ ∣ x ) = p ( x ∣ θ ) p ( θ ) p ( x ) ⇒ argmax p ( θ ∣ x ) p(x|\theta)p(\theta)=p(\theta|x)p(x)\Rightarrow p(\theta|x)=\frac{p(x|\theta)p(\theta)}{p(x)}\Rightarrow\operatorname{argmax}p(\theta|x) p(x∣θ)p(θ)=p(θ∣x)p(x)⇒p(θ∣x)=p(x)p(x∣θ)p(θ)⇒argmaxp(θ∣x)
极大似然估计:
θ ^ = arg max θ log P ( Y ∣ θ ) \hat \theta = \arg\max\limits_{\theta}\log P(Y|\theta) θ^=argθmaxlogP(Y∣θ)
极大后验概率:
argmax p ( θ ∣ x ) ⟺ argmax p ( x ∣ θ ) p ( θ ) \text{argmax} \ p(\theta|x)\iff\text {argmax} \ p(x|\theta)p(\theta) argmax p(θ∣x)⟺argmax p(x∣θ)p(θ)
均匀分布下,后一部分是等概率的,N
KL散度=交叉熵+const
三硬币模型的EM算法
1.初值
EM算法首选参数初值,记作 θ ( 0 ) = ( π ( 0 ) , p ( 0 ) , q ( 0 ) ) \theta^{(0)}=(\pi^{(0)},p^{(0)}, q^{(0)}) θ(0)=(π(0),p(0),q(0)), 然后迭代计算参数的估计值。
如果第 i i i次迭代的模型参数估计值为 θ ( i ) = ( π ( i ) , p ( i ) , q ( i ) ) \theta^{(i)}=(\pi^{(i)}, p^{(i)}, q^{(i)}) θ(i)=(π(i),p(i),q(i))
2.E步
那么第 i + 1 i+1 i+1 次迭代的模型参数估计值表示为
μ j i + 1 = π ( i ) ( p ( i ) ) y j ( 1 − p ( i ) ) 1 − y j π ( i ) ( p ( i ) ) y j ( 1 − p ( i ) ) 1 − y j + ( 1 − π ( i ) ) ( q ( i ) ) y j ( 1 − q ( i ) ) 1 − y j \mu_j^{i+1} = \frac{\pi^{(i)}(p^{(i)})^{y_j}(1-p^{(i)})^{1-y_j}}{\pi^{(i)}(p^{(i)})^{y_j}(1-p^{(i)})^{1-y_j} + (1-\pi^{(i)})(q^{(i)})^{y_j}(1-q^{(i)})^{1-y_j}} μji+1=π(i)(p(i))yj(1−p(i))1−yj+(1−π(i))(q(i))yj(1−q(i))1−yjπ(i)(p(i))yj(1−p(i))1−yj
因为是硬币,只有0,1两种可能,所有有上面的表达
这个表达方式还可以拆成如下形式
μ j i + 1 = { π ( i ) p ( i ) π ( i ) p ( i ) + ( 1 − π ( i ) ) q ( i ) , y j = 1 π ( i ) ( 1 − p ( i ) ) π ( i ) ( 1 − p ( i ) ) + ( 1 − π ( i ) ) ( 1 − q ( i ) ) , y j = 0 \mu_j^{i+1} = \begin{cases} \frac{\pi^{(i)}p^{(i)}}{\pi^{(i)}p^{(i)} + (1-\pi^{(i)})q^{(i)}}&, y_j = 1\\ \frac{\pi^{(i)}(1-p^{(i)})}{\pi^{(i)}(1-p^{(i)}) + (1-\pi^{(i)})(1-q^{(i)})}&, y_j = 0\\ \end{cases} μji+1=⎩ ⎨ ⎧π(i)p(i)+(1−π(i))q(i)π(i)p(i)π(i)(1−p(i))+(1−π(i))(1−q(i))π(i)(1−p(i)),yj=1,yj=0
所以, 这步(求 μ j \mu_j μj)干了什么,样本起到了什么作用?
这一步,通过假设的参数,计算了不同的样本对假设模型的响应( μ j \mu_j μj),注意这里因为样本( y j y_j yj)是二值的,所以,用 { y j , 1 − y j } \{y_j, 1-y_j\} {yj,1−yj} 构成了one-hot的编码,用来表示样本归属的假设
以上,有点绕
这一步是什么的期望?书中有写,**观测数据来自硬币 B B B的概率, 在二项分布的情况下, 响应度和概率是一个概念. **这个说明,有助于后面M步公式的理解。
3.M步
π ( i + 1 ) = 1 n ∑ j = 1 n μ j ( i + 1 ) p ( i + 1 ) = ∑ j = 1 n μ j ( i + 1 ) y j ∑ j = 1 n μ j ( i + 1 ) q ( i + 1 ) = ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) y j ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) \begin{align} \pi^{(i+1)} &= \frac{1}{n}\sum_{j=1}^{n}\mu_j^{(i+1)}\\ \color{red} p^{(i+1)} &= \frac{\sum_{j=1}^{n}\mu_j^{(i+1)}y_j}{\sum_{j=1}^{n}\mu_j^{(i+1)}}\\ \color{red} q^{(i+1)} &= \frac{\sum_{j=1}^{n}(1-\mu_j^{(i+1)})y_j}{\sum_{j=1}^{n}(1-\mu_j^{(i+1)})} \end{align} π(i+1)p(i+1)q(i+1)=n1j=1∑nμj(i+1)=∑j=1nμj(i+1)∑j=1nμj(i+1)yj=∑j=1n(1−μj(i+1))∑j=1n(1−μj(i+1))yj
上面,红色部分的公式从观测数据是来自硬币B的概率这句来理解
初值影响
这个例子里面0.5是个合理又牛逼的初值。迭代收敛的最后结果是(0.5, 0.6, 0.6)
这个结果说明,如果A是均匀的,那么一个合理的解就是B,C是同质的。他们的分布情况和观测的分布一致
p,q 含义
这里面 p p p对应了 A = 1 A =1 A=1, B = 1 B=1 B=1, q q q对应了 A = 0 A=0 A=0, C = 1 C=1 C=1
这三个公式可以改写成如下形式:
π ( i + 1 ) = 1 n ∑ j = 1 n μ j ( i + 1 ) p ( i + 1 ) = ∑ j = 1 n μ j ( i + 1 ) y j ∑ j = 1 n ( μ j ( i + 1 ) y j + μ j ( i + 1 ) ( 1 − y j ) q ( i + 1 ) = ∑ j = 1 n ( 1 − μ j ( i + 1 ) ) y j ∑ j = 1 n ( ( 1 − μ j ( i + 1 ) ) y j + ( 1 − μ j ( i + 1 ) ) ( 1 − y j ) ) \begin{align} \pi^{(i+1)} &= \frac{1}{n}\sum_{j=1}^{n}\mu_j^{(i+1)}\\ \color{red} p^{(i+1)} &= \frac{\sum_{j=1}^{n}\mu_j^{(i+1)}y_j}{\sum_{j=1}^{n}(\mu_j^{(i+1)}y_j+\mu_j^{(i+1)}(1-y_j)}\\ \color{red} q^{(i+1)} &= \frac{\sum_{j=1}^{n}(1-\mu_j^{(i+1)})y_j}{\sum_{j=1}^{n}((1-\mu_j^{(i+1)})y_j+(1-\mu_j^{(i+1)})(1-y_j))} \end{align} π(i+1)p(i+1)q(i+1)=n1j=1∑nμj(i+1)=∑j=1n(μj(i+1)yj+μj(i+1)(1−yj)∑j=1nμj(i+1)yj=∑j=1n((1−μj(i+1))yj+(1−μj(i+1))(1−yj))∑j=1n(1−μj(i+1))yj
π \pi π的表达式回答这样一个问题: 刷了这么多样本,拿到一堆数,那么 π \pi π应该是多少,均值是个比较好的选择
p p p的表达式回答这样一个问题: 如果我知道每个结果 y j y_j yj以 μ j \mu_j μj的可能来自硬币B(A=1),那么用这些数据刷出来他可能是正面的概率。这里面 μ j \mu_j μj对应了 A = 1 A=1 A=1
q q q的表达式同理,其中 1 − μ j 1-\mu_j 1−μj对应了 A = 0 A=0 A=0
到后面讲高斯混合模型的时候,可以重新审视这里
α 0 ↔ π μ 0 ↔ p y j ( 1 − p ) 1 − y j α 1 ↔ 1 − π μ 1 ↔ q y j ( 1 − q ) 1 − y j \begin{aligned} \alpha_0& \leftrightarrow \pi \\ \mu_0& \leftrightarrow p^{y_j}(1-p)^{1-y_j}\\ \alpha_1& \leftrightarrow 1-\pi\\ \mu_1& \leftrightarrow q^{y_j}(1-q)^{1-y_j} \end{aligned} α0μ0α1μ1↔π↔pyj(1−p)1−yj↔1−π↔qyj(1−q)1−yj
以上对应了包含两个分量的伯努利混合模型
bmm.py对伯努利混合模型做了实现, 有几点说明一下:
-
( p ( i ) ) y i ( 1 − p ( i ) ) 1 − y i (p^{(i)})^{y_i}(1-p^{(i)})^{1-y_i} (p(i))yi(1−p(i))1−yi这个表达式对应了伯努利分布的概率密度,可以表示成矩阵乘法,尽量不要用for,效率会差
-
采用了 π , p , q \pi, p, q π,p,q来表示,注意在题目的说明部分有说明三个符号的含义
-
实际上不怎么抛硬币,但是0-1的伯努利分布很多
当参数 θ \theta θ的维数为 d ( d ≥ 2 ) d(d\ge2 ) d(d≥2)的时候,可以采用一种特殊的GEM算法,它将算法的M步分解成d次条件极大化,每次只改变参数向量的一个分量,其余量不改变。
EM算法另外视角
输入: 观测变量数据 Y Y Y,隐变量数据 Z Z Z,联合分布 P ( Y , Z ∣ θ ) P(Y,Z|\theta) P(Y,Z∣θ),条件分布 P ( Z ∣ Y , θ ) P(Z|Y,\theta) P(Z∣Y,θ)
输出: 模型参数 θ \theta θ
选择参数的初值 θ ( 0 ) \theta^{(0)} θ(0),开始迭代
E步:记 θ ( i ) \theta^{(i)} θ(i)为第 i i i 次迭代参数 θ \theta θ的估计值,在第 i + 1 i+1 i+1次迭代的 E E E步,计算
Q ( θ , θ ( i ) ) = E Z [ log P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ] = ∑ Z log P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) \begin{align} Q(\theta, \theta^{(i)}) =& E_Z[\log P(Y,Z|\theta)|Y,\theta^{(i)}]\\ =&\sum_Z\color{red}\log P(Y,Z|\theta)\color{green}P(Z|Y, \theta^{(i)}) \end{align} Q(θ,θ(i))==EZ[logP(Y,Z∣θ)∣Y,θ(i)]Z∑logP(Y,Z∣θ)P(Z∣Y,θ(i))M步
求使 Q ( θ , θ ( i ) ) Q(\theta, \theta^{(i)}) Q(θ,θ(i))最大化的 θ \theta θ,确定第 i + 1 i+1 i+1次迭代的参数估计值θ ( i + 1 ) = arg max θ Q ( θ , θ ( i ) ) \theta^{(i+1)}=\arg\max_\theta Q(\theta, \theta^{(i)}) θ(i+1)=argθmaxQ(θ,θ(i))
Q 函数
注意Q函数的定义,可以帮助理解上面E步中的求和表达式
完全数据的对数似然函数 log P ( Y , Z ∣ θ ) \log P(Y, Z|\theta) logP(Y,Z∣θ)关于给定观测数据 Y Y Y的当前参数 θ ( i ) \theta^{(i)} θ(i)下对为观测数据 Z Z Z的条件概率分布 P ( Z ∣ Y , θ ( i ) ) P(Z|Y,\theta^{(i)}) P(Z∣Y,θ(i))的期望称为Q函数
BMM的EM算法
输入: 观测变量数据 y 1 , y 2 , … , y N y_1, y_2, \dots, y_N y1,y2,…,yN,伯努利混合模型
输出: 伯努利混合模型参数
- 选择参数的初始值开始迭代, 2 K 2K 2K 个参数
- E步:
γ ^ j k = α k B e r n ( y j ∣ θ k ) ∑ k = 1 K α k B e r n ( y j ∣ θ k ) = α k μ k y j ( 1 − μ k ) 1 − y j ∑ k = 1 K α k μ k y j ( 1 − μ k ) 1 − y j , j = 1 , 2 , … , N ; k = 1 , 2 , … , K \hat\gamma_{jk}=\frac{\alpha_kBern(y_j|\theta_k)}{\sum_{k=1}^K\alpha_kBern(y_j|\theta_k)}=\frac{\alpha_k\mu_k^{y_j}(1-\mu_k)^{1-y_j}}{\sum_{k=1}^K\alpha_k\mu_k^{y_j}(1-\mu_k)^{1-y_j}}, j=1,2,\dots,N; k=1,2,\dots,K γ^jk=∑k=1KαkBern(yj∣θk)αkBern(yj∣θk)=∑k=1Kαkμkyj(1−μk)1−yjαkμkyj(1−μk)1−yj,j=1,2,…,N;k=1,2,…,K- M步:
μ ^ k = ∑ j = 1 N γ ^ j k y j ∑ j = 1 N γ ^ j k α ^ k = n k N \hat\mu_k=\frac{\sum_{j=1}^N\hat\gamma_{jk}y_j}{\sum_{j=1}^N\hat\gamma_{jk}}\\ \hat\alpha_k=\frac{n_k}{N} μ^k=∑j=1Nγ^jk∑j=1Nγ^jkyjα^k=Nnk
目标函数L
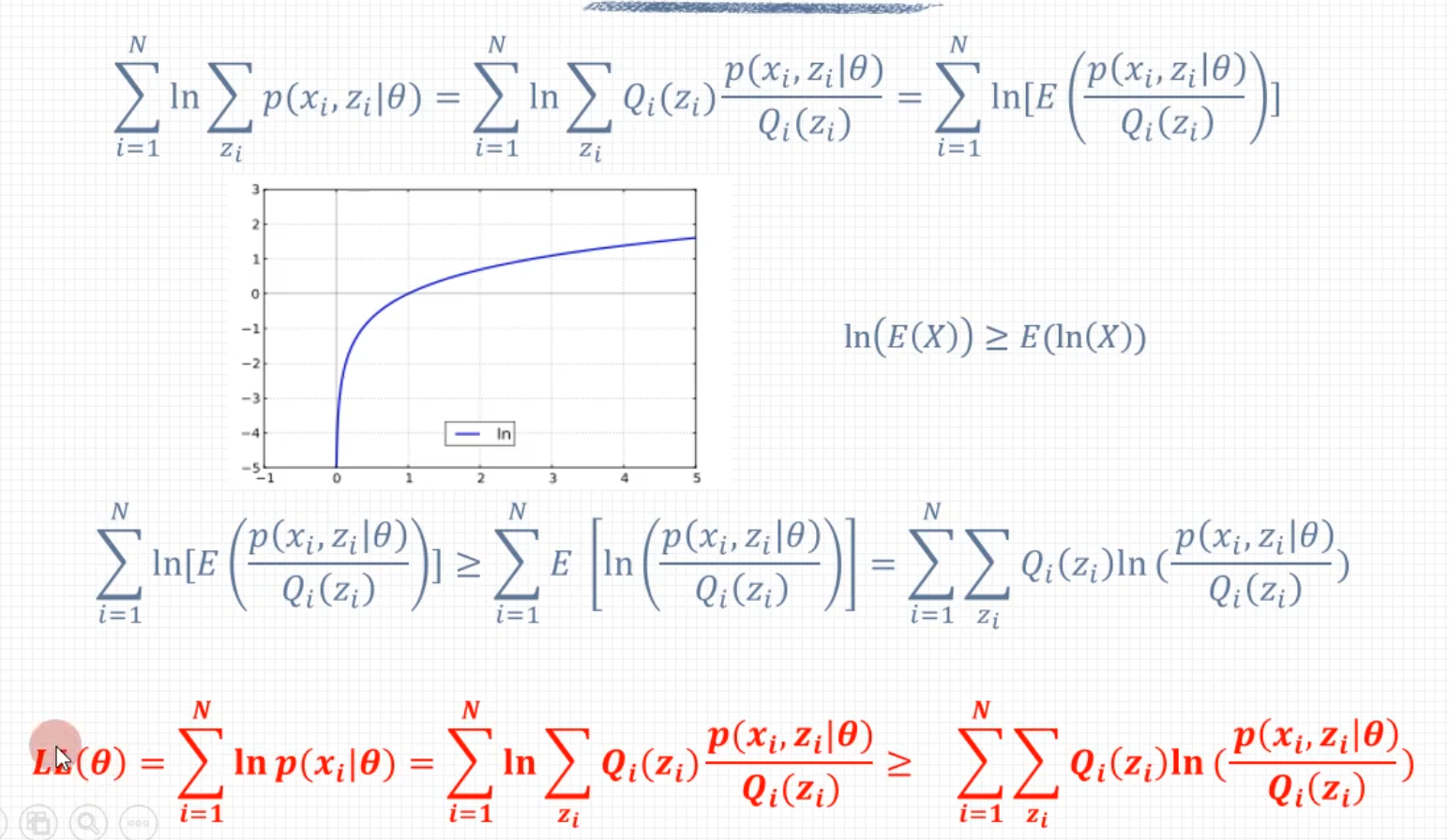
L ( θ ) = log P ( Y ∣ θ ) = log ∑ Z P ( Y , Z ∣ θ ) = log ( ∑ Z P ( Y ∣ Z , θ ) P ( Z ∣ θ ) ) L(\theta)=\log P(Y|\theta)=\log \sum_Z P(Y,Z|\theta)=\log(\sum_Z P(Y|Z,\theta)P(Z|\theta)) L(θ)=logP(Y∣θ)=logZ∑P(Y,Z∣θ)=log(Z∑P(Y∣Z,θ)P(Z∣θ))
目标函数是不完全数据的对数似然
EM算法导出
书中这部分内容回答为什么EM算法能近似实现对观测数据的极大似然估计?
L ( θ ) − L ( θ ( i ) ) = log ( ∑ Z P ( Z ∣ Y , θ ( i ) ) P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) ) − log P ( Y ∣ θ ( i ) ) ≥ ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) − log P ( Y ∣ θ ( i ) ) = ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) − ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ θ ( i ) ) = ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) P ( Y ∣ θ ( i ) ) \begin{align} L(\theta)-L(\theta^{(i)})&=\log \left(\sum_Z\color{green}P(Z|Y,\theta^{(i)})\frac{P(Y|Z,\theta)P(Z|\theta)}{\color{green}P(Z|Y,\theta^{(i)})}\right)-\log P(Y|\theta^{(i)})\\ &\ge\sum_Z \color{green}P(Z|Y,\theta^{(i)})\log \frac{P(Y|Z,\theta)P(Z|\theta)}{\color{green}P(Z|Y,\theta^{(i)})}-\log P(Y|\theta^{(i)})\\ &=\sum_Z P(Z|Y,\theta^{(i)})\log \frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})}-\color{red}\sum_Z P(Z|Y,\theta^{(i)})\color{black}\log P(Y|\theta^{(i)})\\ &=\sum_ZP(Z|Y,\theta^{(i)})\log \frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})} \end{align} L(θ)−L(θ(i))=log(Z∑P(Z∣Y,θ(i))P(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))≥Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ)−logP(Y∣θ(i))=Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ)−Z∑P(Z∣Y,θ(i))logP(Y∣θ(i))=Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣θ(i))P(Y∣Z,θ)P(Z∣θ)
以上用于推导迭代过程中两次 L L L会变大, 这里面红色部分是后加的方便理解前后两步之间的推导。绿色部分是为了构造期望, 进而应用琴声不等式
高斯混合模型
混合模型,有多种,高斯混合模型是最常用的
高斯混合模型(Gaussian Mixture Model)是具有如下概率分布的模型:
P ( y ∣ θ ) = ∑ k = 1 K α k ϕ ( y ∣ θ k ) P(y|\theta)=\sum\limits^{K}_{k=1}\alpha_k\phi(y|\theta_k) P(y∣θ)=k=1∑Kαkϕ(y∣θk)
其中, α k \alpha_k αk是系数, α k ≥ 0 \alpha_k\ge0 αk≥0, ∑ k = 1 K α k = 1 \sum\limits^{K}_{k=1}\alpha_k=1 k=1∑Kαk=1, ϕ ( y ∣ θ k ) \phi(y|\theta_k) ϕ(y∣θk) 是高斯分布密度, θ k = ( μ , σ 2 ) \theta_k=(\mu,\sigma^2) θk=(μ,σ2)
ϕ ( y ∣ θ k ) = 1 2 π σ k exp ( − ( y − μ k ) 2 2 σ k 2 ) \phi(y|\theta_k)=\frac{1}{\sqrt{2\pi}\sigma_k}\exp\left(-\frac{(y-\mu_k)^2}{2\sigma_k^2}\right) ϕ(y∣θk)=2πσk1exp(−2σk2(y−μk)2)
上式表示第k个分模型
以上, 注意几点:
-
GMM的描述是概率分布,形式上可以看成是加权求和,有啥用?
-
加权求和的权重 α \alpha α满足 ∑ k = 1 K α k = 1 \sum_{k=1}^K\alpha_k=1 ∑k=1Kαk=1的约束
-
求和符号中除去权重的部分,是高斯分布密度(PDF)。高斯混合模型是一种 ∑ ( 权重 × 分布密度 ) = 分布 \sum(权重\times 分布密度)=分布 ∑(权重×分布密度)=分布的表达
高斯混合模型的参数估计是EM算法的一个重要应用,隐马尔科夫模型的非监督学习也是EM算法的一个重要应用 -
书中描述的是一维的高斯混合模型,d维的形式如下[^2],被称作多元正态分布,也叫多元高斯分布
ϕ ( y ∣ θ k ) = 1 ( 2 π ) d ∣ Σ ∣ exp ( − ( y − μ k ) T Σ − 1 ( y − μ k ) 2 ) \phi(y|\theta_k)=\frac{1}{\sqrt{(2\pi)^d|\Sigma|}}\exp\left(-\frac{(y-\mu_k)^T\Sigma^{-1}(y-\mu_k)}{2}\right) ϕ(y∣θk)=(2π)d∣Σ∣1exp(−2(y−μk)TΣ−1(y−μk))
其中,协方差矩阵 Σ ∈ R n × n \Sigma\in \R^{n\times n} Σ∈Rn×n -
另外,关于高斯模型的混合,还有另外一种混合的方式,沿着时间轴的方向做混合。可以理解为滤波器,典型的算法就是Kalman Filter,对应了时域与频域之间的关系,两个高斯的混合依然是高斯,混合的方法是卷积,而不是简单的加法,考虑到的是概率密度的混合,也是一种线性的加权
GMM的EM算法
问题描述:
已知观测数据 y 1 , y 2 , … , y N y_1, y_2, \dots , y_N y1,y2,…,yN,由高斯混合模型生成
P ( y ∣ θ ) = ∑ k = 1 K α k ϕ ( y ∣ θ k ) P(y|\theta)=\sum_{k=1}^K\alpha_k\phi(y|\theta_k) P(y∣θ)=k=1∑Kαkϕ(y∣θk)
其中, θ = ( α 1 , α 2 , … , α K ; θ 1 , θ 2 , … , θ K ) \theta=(\alpha_1,\alpha_2,\dots,\alpha_K;\theta_1,\theta_2,\dots,\theta_K) θ=(α1,α2,…,αK;θ1,θ2,…,θK)
补充下,不完全数据的似然函数应该是
P ( y ∣ θ ) = ∏ j = 1 N P ( y j ∣ θ ) = ∏ j = 1 N ∑ k = 1 K α k ϕ ( y ∣ θ k ) \begin{align} P(y|\theta)=&\prod_{j=1}^NP(y_j|\theta)\\ =&\prod_{j=1}^N\sum_{k=1}^K\alpha_k\phi(y|\theta_k) \end{align} P(y∣θ)==j=1∏NP(yj∣θ)j=1∏Nk=1∑Kαkϕ(y∣θk)
使用EM算法估计GMM的参数 θ \theta θ
1. 明确隐变量, 初值
-
观测数据 y j , j = 1 , 2 , … , N y_j, j=1,2,\dots,N yj,j=1,2,…,N这样产生, 是已知的:
-
依概率 α k \alpha_k αk选择第 k k k个高斯分布分模型 ϕ ( y ∣ θ k ) \phi(y|\theta_k) ϕ(y∣θk);
-
依第 k k k个分模型的概率分布 ϕ ( y ∣ θ k ) \phi(y|\theta_k) ϕ(y∣θk)生成观测数据 y j y_j yj
-
反映观测数据 y j y_j yj来自第 k k k个分模型的数据是未知的, k = 1 , 2 , … , K k=1,2,\dots,K k=1,2,…,K 以**隐变量 γ j k \gamma_{jk} γjk**表示
注意这里 γ j k \gamma_{jk} γjk的维度 ( j × k ) (j\times k) (j×k)
γ j k = { 1 , 第 j 个观测来自第 k 个分模型 0 , 否则 j = 1 , 2 , … , N ; k = 1 , 2 , … , K ; γ j k ∈ { 0 , 1 } \gamma_{jk}= \begin{cases} 1, &第j个观测来自第k个分模型\\ 0, &否则 \end{cases}\\ j=1,2,\dots,N; k=1,2,\dots,K; \gamma_{jk}\in\{0,1\} γjk={1,0,第j个观测来自第k个分模型否则j=1,2,…,N;k=1,2,…,K;γjk∈{0,1}
注意, 以上说明有几个假设: -
隐变量和观测变量的数据对应, 每个观测数据,对应了一个隐变量, γ j k \gamma_{jk} γjk是一种one-hot的形式。
-
具体的单一观测数据是混合模型中的某一个模型产生的
-
-
完全数据为 ( y j , γ j 1 , γ j 2 , … , γ j K , k = 1 , 2 , … , N ) (y_j,\gamma_{j1},\gamma_{j2},\dots,\gamma_{jK},k=1,2,\dots,N) (yj,γj1,γj2,…,γjK,k=1,2,…,N)
-
完全数据似然函数
P ( y , γ ∣ θ ) = ∏ j = 1 N P ( y j , γ j 1 , γ j 2 , … , γ j K ∣ θ ) = ∏ k = 1 K ∏ j = 1 N [ α k ϕ ( y j ∣ θ k ) ] γ j k = ∏ k = 1 K α k n k ∏ j = 1 N [ ϕ ( y j ∣ θ k ) ] γ j k = ∏ k = 1 K α k n k ∏ j = 1 N [ 1 2 π σ k exp ( − ( y j − μ k ) 2 2 σ 2 ) ] γ j k \begin{aligned} P(y,\gamma|\theta)=&\prod_{j=1}^NP(y_j,\gamma_{j1},\gamma_{j2},\dots,\gamma_{jK}|\theta)\\ =&\prod_{k=1}^K\prod_{j=1}^N\left[\alpha_k\phi(y_j|\theta_k)\right]^{\gamma_{jk}}\\ =&\prod_{k=1}^K\alpha_k^{n_k}\prod_{j=1}^N\left[\phi(y_j|\theta_k)\right]^{\gamma_{jk}}\\ =&\prod_{k=1}^K\alpha_k^{n_k}\prod_{j=1}^N\left[\frac{1}{\sqrt{2\pi}\sigma_k}\exp\left(-\frac{(y_j-\mu_k)^2}{2\sigma^2}\right)\right]^{\gamma_{jk}}\\ \end{aligned} P(y,γ∣θ)====j=1∏NP(yj,γj1,γj2,…,γjK∣θ)k=1∏Kj=1∏N[αkϕ(yj∣θk)]γjkk=1∏Kαknkj=1∏N[ϕ(yj∣θk)]γjkk=1∏Kαknkj=1∏N[2πσk1exp(−2σ2(yj−μk)2)]γjk
其中 n k = ∑ j = 1 N γ j k , ∑ k = 1 K n k = N n_k=\sum_{j=1}^N\gamma_{jk}, \sum_{k=1}^Kn_k=N nk=∑j=1Nγjk,∑k=1Knk=N -
完全数据对数似然函数
log P ( y , γ ∣ θ ) = ∑ k = 1 K { n k log α k + ∑ j = 1 N γ j k [ log ( 1 2 π ) − log σ k − 1 2 σ 2 ( y j − μ k ) 2 ] } \log P(y,\gamma|\theta)=\sum_{k=1}^K\left\{n_k\log \alpha_k+\sum_{j=1}^N\gamma_{jk}\left[\log \left(\frac{1}{\sqrt{2\pi}}\right)-\log \sigma_k -\frac{1}{2\sigma^2}(y_j-\mu_k)^2\right]\right\} logP(y,γ∣θ)=k=1∑K{nklogαk+j=1∑Nγjk[log(2π1)−logσk−2σ21(yj−μk)2]}
2. E步,确定Q函数
把 Q Q Q 函数表示成参数形式
Q ( θ , θ ( i ) ) = E [ log P ( y , γ ∣ θ ) ∣ y , θ ( i ) ] = E ∑ k = 1 K n k log α k + ∑ j = 1 N γ j k [ log ( 1 2 π ) − log σ k − 1 2 σ 2 ( y j − μ k ) 2 ] = E ∑ k = 1 K ∑ j = 1 N γ j k log α k + ∑ j = 1 N γ j k [ log ( 1 2 π ) − log σ k − 1 2 σ 2 ( y j − μ k ) 2 ] = ∑ k = 1 K ∑ j = 1 N ( E γ j k ) log α k + ∑ j = 1 N ( E γ j k ) [ log ( 1 2 π ) − log σ k − 1 2 σ 2 ( y j − μ k ) 2 ] \begin{aligned}Q(\theta,\theta^{(i)}) =&E[\log P(y,\gamma|\theta)|y,\theta^{(i)}]\\ =&\color{green}E\color{black}{\sum_{k=1}^K{\color{red}n_k\color{black}\log \alpha_k+\color{blue}\sum_{j=1}^N\gamma _{jk}\color{black}[\log(\frac{1}{\sqrt{2\pi}})-\log \sigma _k-\frac{1}{2\sigma^2(y_j-\mu_k)^2}]}}\\ =&\color{green}E\color{black}{\sum_{k=1}^K{\color{red}\sum_{j=1}^N\gamma_{jk}\color{black}\log \alpha_k+\color{blue}\sum_{j=1}^N\gamma _{jk}\color{black}[\log (\frac{1}{\sqrt{2\pi}})-\log \sigma _k-\frac{1}{2\sigma^2(y_j-\mu_k)^2}]}}\\ =&\sum_{k=1}^K{\color{red}\sum_{j=1}^{N}(\color{green}E\color{red}\gamma_{jk})\color{black}\log \alpha_k+\color{blue}\sum_{j=1}^N(\color{green}E\color{blue}\gamma _{jk})\color{black}[\log (\frac{1}{\sqrt{2\pi}})-\log \sigma _k-\frac{1}{2\sigma^2(y_j-\mu_k)^2}]}\\ \end{aligned} Q(θ,θ(i))====E[logP(y,γ∣θ)∣y,θ(i)]Ek=1∑Knklogαk+j=1∑Nγjk[log(2π1)−logσk−2σ2(yj−μk)21]Ek=1∑Kj=1∑Nγjklogαk+j=1∑Nγjk[log(2π1)−logσk−2σ2(yj−μk)21]k=1∑Kj=1∑N(Eγjk)logαk+j=1∑N(Eγjk)[log(2π1)−logσk−2σ2(yj−μk)21]
γ ^ j k = E ( γ j k ∣ y , θ ) = P ( γ j k = 1 ∣ y , θ ) = P ( γ j k = 1 , y j ∣ θ ) ∑ k = 1 K P ( γ j k = 1 , y j ∣ θ ) = P ( y j ∣ γ j k = 1 , θ ) P ( γ j k = 1 ∣ θ ) ∑ k = 1 K P ( y j ∣ γ j k = 1 , θ ) P ( γ j k = 1 ∣ θ ) = α k ϕ ( y j ∣ θ k ) ∑ k = 1 K α k ϕ ( y j ∣ θ k ) \begin{aligned}\hat \gamma _{jk}= &\color{purple}E(\gamma_{jk}|y,\theta)=P(\gamma_{jk}=1|y,\theta)\\=&\frac{P(\gamma_{jk}=1,y_j|\theta)}{\sum_{k=1}^KP(\gamma_{jk}=1,y_j|\theta)}\\=&\frac{P(y_j|\color{red}\gamma_{jk}=1,\theta\color{black})\color{green}P(\gamma_{jk}=1|\theta)}{\sum_{k=1}^KP(y_j|\gamma_{jk}=1,\theta)P(\gamma_{jk}=1|\theta)}\\=&\frac{\color{green}\alpha_k\color{black}\phi(y_j|\color{red}\theta_k)}{\sum_{k=1}^K\alpha_k\phi(y_j|\theta_k)}\end{aligned} γ^jk====E(γjk∣y,θ)=P(γjk=1∣y,θ)∑k=1KP(γjk=1,yj∣θ)P(γjk=1,yj∣θ)∑k=1KP(yj∣γjk=1,θ)P(γjk=1∣θ)P(yj∣γjk=1,θ)P(γjk=1∣θ)∑k=1Kαkϕ(yj∣θk)αkϕ(yj∣θk)
这部分内容就是搬运了书上的公式,有几点说明:
- 注意这里 E ( γ j k ∣ y , θ ) E(\gamma_{jk}|y,\theta) E(γjk∣y,θ),记为 γ ^ j k \hat\gamma_{jk} γ^jk, 对应了E步求的期望中的一部分。
- 对应理解一下上面公式中的红色,蓝色和绿色部分,以及 γ ^ j k \hat\gamma_{jk} γ^jk中红色和绿色的对应关系
- 这里用到了 n k = ∑ j = 1 N γ j k n_k=\sum_{j=1}^N\gamma_{jk} nk=∑j=1Nγjk
- γ ^ j k \hat \gamma_{jk} γ^jk为分模型 k k k对观测数据 y j y_j yj的响应度。这里,紫色标记的第一行参考伯努利分布的期望。
Q ( θ , θ ( i ) ) = ∑ k = 1 K n k log α k + ∑ j = 1 N γ ^ j k [ log ( 1 2 π ) − log σ k − 1 2 σ k 2 ( y j − μ k ) 2 ] Q(\theta,\theta^{(i)})=\sum_{k=1}^Kn_k\log \alpha_k+\sum_{j=1}^N\hat \gamma_{jk}\left[\log \left(\frac{1}{\sqrt{2\pi}}\right)-\log \sigma_k-\frac{1}{2\sigma_k^2}(y_j-\mu_k)^2\right] Q(θ,θ(i))=k=1∑Knklogαk+j=1∑Nγ^jk[log(2π1)−logσk−2σk21(yj−μk)2]
其中 i i i表示第 i i i步迭代
- 写出 Q Q Q 函数在推导的时候有用,但是在程序计算的时候,E步需要计算的就是 γ ^ j k \hat\gamma_{jk} γ^jk,M步用到了这个结果。其实抄公式没有什么意义,主要是能放慢看公式的速度。和图表一样,公式简洁的表达了很多信息,公式中也许更能体会到数学之美。
3. M步
求函数 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))对 θ \theta θ的极大值,分别求 σ , μ , α \sigma, \mu, \alpha σ,μ,α
θ ( i + 1 ) = arg max θ Q ( θ , θ ( i ) ) \theta^{(i+1)}=\arg\max_\theta Q(\theta,\theta^{(i)}) θ(i+1)=argθmaxQ(θ,θ(i))
- arg max \arg\max argmax 就是求Q的极值对应的参数 θ \theta θ,如说是离散的,遍历所有值,最大查找,如果是连续的,偏导为零求极值。
- ∂ Q ∂ μ k = 0 , ∂ Q ∂ σ 2 = 0 \frac {\partial Q}{\partial \mu_k}=0, \frac {\partial{Q}}{\partial{\sigma^2}}= 0 ∂μk∂Q=0,∂σ2∂Q=0 得到 μ ^ k , σ ^ k 2 \hat\mu_k, \hat \sigma_k^2 μ^k,σ^k2
- ∑ k = 1 K α k = 1 , ∂ Q ∂ α k = 0 \sum_{k=1}^K\alpha_k=1, \frac{\partial{Q}}{\partial{\alpha_k}}=0 ∑k=1Kαk=1,∂αk∂Q=0 得到 α k \alpha_k αk
4. 停止条件
重复以上计算,直到对数似然函数值不再有明显的变化为止。
如何应用
GMM在聚类中的应用
使用EM算法估计了GMM的参数之后,有新的数据点,怎么计算样本的类别的?
在机器学习[^5]中有一些关于聚类的表述,摘录这里:
Gaussian mixture modeling is among the popular clustering algorithms. The main assumption is that the points, which belong to the same cluster, are distributed according to the same Gaussian distribution(this is how similarity is defined in this case), of unknown mean and covariance matrix.
Each mixture component defines a different cluster. Thus, the goal is to run the EM algorithm over the available data points to provide, after convergence, the posterior probabilities P ( k ∣ x n ) , k = 1 , 2 , . . . , K , n = 1 , 2 , . . . , N P(k|x_n), k=1,2,...,K, n=1,2,...,N P(k∣xn),k=1,2,...,K,n=1,2,...,N, where each k corresponds to a cluster. Then each point is assigned to cluster k k k according to the rule.
Assign x n x_n xnto cluster k = arg m a x P ( i ∣ x n ) , i = 1 , 2 , . . . , K k=\arg max P(i|x_n), i =1,2,...,K k=argmaxP(i∣xn),i=1,2,...,K
可以参考下scikit-learn的具体实现,就是用了argmax,选择概率最大的那个输出。
Kmeans
另外,直觉上看,GMM最直观的想法就是Kmeans,那么:
- 在Kmeans常见的描述中都有距离的概念,对应在算法9.2 的描述中,该如何理解?
这里面距离对应了方差,二范数平方 - 那么又是怎么在每轮刷过距离之后,重新划分样本的分类呢?
这里对应了响应度,响应度对应了一个 j × k j \times k j×k的矩阵,记录了每一个 y j y_j yj 对第 k k k个模型的响应度,可以理解为划分了类别
K怎么定
- 手肘法
- Gap Statistics[^1]
- 第二版中,有对应的描述。 P 267 P_{267} P267,一般的类别变大的时候,平均直径会增加,当类别数超过某个值之后,平均直径不会变化,这个值可以是最优的 k k k
相关文章:

第十五章 EM期望极大算法及其推广
文章目录 导读符号说明混合模型伯努利混合模型(三硬币模型)问题描述三硬币模型的EM算法1.初值2.E步3.M步初值影响p,q 含义 EM算法另外视角Q 函数BMM的EM算法目标函数LEM算法导出 高斯混合模型GMM的EM算法1. 明确隐变量, 初值2. E步,确定Q函数3. M步4. 停止条件 如何应用GMM在聚…...

自动化测试如何准备测试数据
其实大部分类型的测试都需要去准备测试数据。 手工测试:一些基础数据,比如配置数据等等是需要去准备的;自动化测试:基础需要准备,现有数据,动态运行时产生的数据是需要准备的;性能测试…...

javaEE -13(6000字CSS入门级教程 - 2)
一:Chrome 调试工具 – 查看 CSS 属性 首先打开浏览器,接着有两种方式可以打开 Chrome 调试工具 直接按 F12 键鼠标右键页面 > 检查元素 点开检查即可 标签页含义: elements 查看标签结构console 查看控制台source 查看源码断点调试ne…...

vscode 使用python无法导入库
刚刚在使用vscode,编辑python时,在使用语句 import matplotlib.pyplot as plt 时出现报错,但是在命令行下和conda环境中没有报错 在尝试 pip uninstall matplotlib pip install matplotlib后无法解决 之后再发现是工作的目录出错导致的,…...
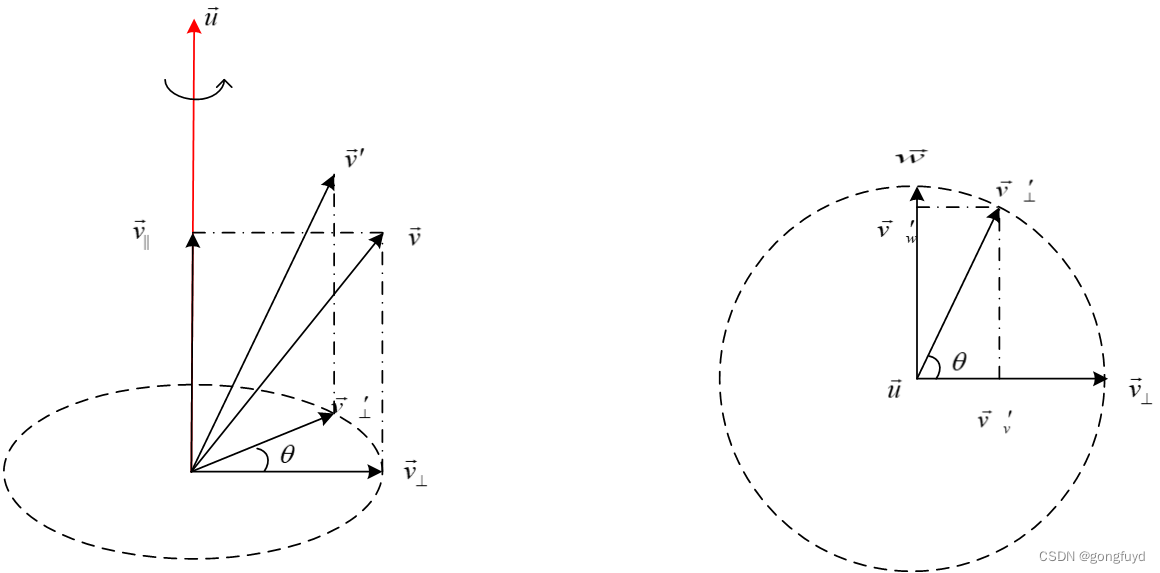
三维向量旋转
三维向量旋转 问题描述问题分析 v ⃗ ∣ ∣ \vec{v}_{||} v ∣∣的旋转 v ⃗ ⊥ \vec{v}_{\bot} v ⊥的旋转 v ⃗ \vec{v} v 的旋转结论致谢 问题描述 如图1所示,设一个向量 v ⃗ \vec{v} v 绕另一个向量 u ⃗ [ x , y , z ] T \vec{u}[x,y,z]^{T} u [x,y,z]T…...

顺序表——leetcode
原地删除数据 我们的思路这里给的是双指针,给两个指针,从前往后移动,如果不是val就覆盖,如果是我就跳过,大家一定要看到我们的条件是原地修改,所以我们不能另开一个数组来实现我们这道题目。 这里我们给两…...

Kaprekar 7641 - 1467= 6174
package homework;import java.util.Arrays;import util.StringUtil;/*** 数学黑洞数6174,即卡普雷卡尔(Kaprekar)常数, 它的算法如下: 取任意一个4位数(4个数字均为同一个数的除外)࿰…...
李宏毅机器学习笔记.Flow-based Generative Model(补)
文章目录 引子生成问题回顾:GeneratorMath BackgroundJacobian MatrixDeterminant 行列式Change of Variable Theorem简单实例一维实例二维实例 网络G的限制基于Flow的网络构架G的训练Coupling LayerCoupling Layer反函数计算Coupling Layer Jacobian矩阵计算Coupli…...

Java使用Spark入门级非常详细的总结
目录 Java使用Spark入门 环境准备 安装JDK 安装Spark 编写Spark应用程序 创建SparkContext 读取文本文件 计算单词出现次数 运行Spark应用程序 总结 Java使用Spark入门 本文将介绍如何使用Java编写Spark应用程序。Spark是一个快速的、通用的集群计算系统,它可以处理…...
kubernetes集群编排——k8s存储
configmap 字面值创建 kubectl create configmap my-config --from-literalkey1config1 --from-literalkey2config2kubectl get cmkubectl describe cm my-config 通过文件创建 kubectl create configmap my-config-2 --from-file/etc/resolv.confkubectl describe cm my-confi…...

【软件STM32cubeIDE下H73xx配置串口uart1+中断接收/DMA收发+HAL库+简单数据解析-基础样例】
#【软件STM32cubeIDE下H73xx配置串口uart1中断接收/DMA收发HAL库简单数据解析-基础样例】 1、前言2、实验器件3-1、普通收发中断接收实验第一步:代码调试-基本配置(1)基本配置(3)时钟配置(4)保存…...

jdk8和jdk9中接口的新特性
jdk8之前:声明抽象方法,修饰为public abstract。 jdk8:添加声明静态方法,默认方法。 jdk9:添加声明私有方法 jdk8: ①接口中声明的静态方法只能被接口来调用,不能使用其实现类进行调用 静态方法的声明&…...

1-爬虫-requests模块快速使用,携带请求参数,url 编码和解码,携带请求头,发送post请求,携带cookie,响应对象, 高级用法
1 爬虫介绍 2 requests模块快速使用 3 携带请求参数 4 url 编码和解码 4 携带请求头 5 发送post请求 6 携带cookie 7 响应对象 8 高级用法 1 爬虫介绍 # 爬虫是什么?-网页蜘蛛,网络机器人,spider-在互联网中 通过 程序 自动的抓取数据 的过程…...
java商城免费搭建 VR全景商城 saas商城 b2b2c商城 o2o商城 积分商城 秒杀商城 拼团商城 分销商城 短视频商城
1. 涉及平台 平台管理、商家端(PC端、手机端)、买家平台(H5/公众号、小程序、APP端(IOS/Android)、微服务平台(业务服务) 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、Redis 3. 前端框架…...
【TS篇一】TypeScript介绍、使用场景、环境搭建、类和接口
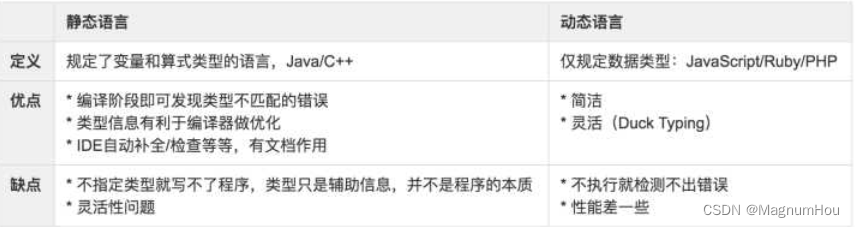
文章目录 一、TypeScript 介绍1. TypeScript 是什么1.2 静态类型和动态类型1.3 Why TypeScript1.4 TypeScript 使用场景1.5 TypeScript 不仅仅用于开发 Angular 应用1.6 前置知识 二、如何学习 TypeScript2.1 相关链接 三、起步3.1 搭建 TypeScript 开发环境3.2 编辑器的选择3.…...

Tuna: Instruction Tuning using Feedback from Large Language Models
本文是LLM系列文章,针对《Tuna: Instruction Tuning using Feedback from Large Language Models》的翻译。 Tuna:使用来自大型语言模型的反馈的指令调优 摘要1 引言2 方法3 实验4 相关工作5 结论局限性 摘要 使用更强大的LLM(如Instruction GPT和GPT-…...

uni-app 应对微信小程序最新隐私协议接口要求的处理方法
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 一,问题起因 最新在开发小程序的时候,调用微信小程序来获取用户信息的时候经常报错一个问题 fail api scope is not declared in the privacy agreement,api更具公告…...
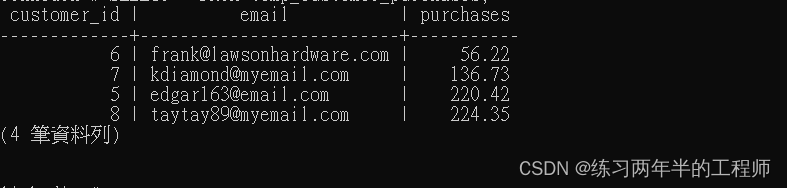
PostgreSQL 进阶 - 使用foreign key,使用 subqueries 插入,inner joins,outer joins
1. 使用foreign key 创建 table CREATE TABLE orders( order_id SERIAL PRIMARY KEY, purchase_total NUMERIC, timestamp TIMESTAMPTZ, customer_id INT REFERENCES customers(customer_id) ON DELETE CASCADE);“order_id”:作为主键的自增序列,使用 …...

【Python 千题 —— 基础篇】地板除计算
题目描述 题目描述 编写一个程序,接受用户输入的两个数字,然后计算这两个数字的地板除(整除)结果,并输出结果。 输入描述 输入两个数字,用回车隔开两个数字。 输出描述 程序将计算这两个数字的地板除…...
函数)
【随手记】np.random.choice()函数
np.random.choice() 是 NumPy 中的一个随机抽样函数,用于从给定的一维数组中随机抽取指定数量或指定概率的元素。该函数可以用于构建模拟实验、生成随机数据集、数据抽样等应用场景。 np.random.choice(a, sizeNone, replaceTrue, pNone) 的参数如下: …...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...