三维向量旋转
三维向量旋转
问题描述
如图1所示,设一个向量 v ⃗ \vec{v} v绕另一个向量 u ⃗ = [ x , y , z ] T \vec{u}=[x,y,z]^{T} u=[x,y,z]T旋转 θ 度,变换到 v ⃗ ′ \vec{v}^{'} v′。
求旋转后得到的向量 v ⃗ ′ \vec{v}^{'} v′的表示形式。

问题分析
由于转轴 u ⃗ \vec{u} u的模长 ∣ ∣ u ⃗ ∣ ∣ ||\vec{u}|| ∣∣u∣∣对旋转结果没有影响,所以可以假设 ∣ ∣ u ⃗ ∣ ∣ = 1 ||\vec{u}||=1 ∣∣u∣∣=1。
可以将 v ⃗ \vec{v} v分解为平行于旋转轴 u ⃗ \vec{u} u以及正交(垂直)于 u ⃗ \vec{u} u的两个分量, v ⃗ ∣ ∣ \vec{v}_{||} v∣∣和 v ⃗ ⊥ \vec{v}_{\bot} v⊥,即 v ⃗ = v ⃗ ∣ ∣ + v ⃗ ⊥ \vec{v}=\vec{v}_{||}+\vec{v}_{\bot} v=v∣∣+v⊥
可以分别旋转这两个分向量,再将它们旋转的结果相加获得旋转后的向量
v ⃗ ′ = v ⃗ ∣ ∣ ′ + v ⃗ ⊥ ′ \vec{v}^{'}=\vec{v}_{||}^{'}+\vec{v}_{\bot}^{'} v′=v∣∣′+v⊥′

可以看到, v ⃗ ∣ ∣ \vec{v}_{||} v∣∣其实就是 v ⃗ \vec{v} v 在 u ⃗ \vec{u} u上的正交投影,根据正交投影的公式,可以得出:
v ⃗ ∣ ∣ = u ⃗ ⋅ v ⃗ u ⃗ ⋅ u ⃗ u ⃗ = u ⃗ ⋅ v ⃗ ∣ ∣ u ⃗ ∣ ∣ 2 u ⃗ \vec{v}_{||} = \frac{\vec{u}\cdot\vec{v}}{\vec{u}\cdot\vec{u}}\vec{u}=\frac{\vec{u}\cdot\vec{v}}{||\vec{u}||^{2}}\vec{u} v∣∣=u⋅uu⋅vu=∣∣u∣∣2u⋅vu
根据 ∣ ∣ u ⃗ ∣ ∣ = 1 ||\vec{u}||=1 ∣∣u∣∣=1,可得: v ⃗ ∣ ∣ = ( u ⃗ ⋅ v ⃗ ) u ⃗ \vec{v}_{||} = (\vec{u}\cdot\vec{v})\vec{u} v∣∣=(u⋅v)u
因为 v ⃗ = v ⃗ ∣ ∣ + v ⃗ ⊥ \vec{v}=\vec{v}_{||}+\vec{v}_{\bot} v=v∣∣+v⊥,所以: v ⃗ ⊥ = v ⃗ − v ⃗ ∣ ∣ = v ⃗ − ( u ⃗ ⋅ v ⃗ ) u ⃗ \vec{v}_{\bot} =\vec{v}-\vec{v}_{||} =\vec{v}-(\vec{u}\cdot\vec{v})\vec{u} v⊥=v−v∣∣=v−(u⋅v)u
分别求 v ⃗ ∣ ∣ \vec{v}_{||} v∣∣和 v ⃗ ⊥ \vec{v}_{\bot} v⊥的旋转结果就能得到 v ⃗ \vec{v} v的旋转结果。
v ⃗ ∣ ∣ \vec{v}_{||} v∣∣的旋转
这种情况其实非常简单,从图2中就可以看到, v ⃗ ∣ ∣ \vec{v}_{||} v∣∣其实根本就没有被旋转,仍然与旋转轴 u ⃗ \vec{u} u重合,所以:
当 v ⃗ ∣ ∣ \vec{v}_{||} v∣∣平行于旋转轴 u ⃗ \vec{u} u时,旋转 θ 角度之后的 v ⃗ ∣ ∣ ′ \vec{v}_{||}^{'} v∣∣′为: v ⃗ ∣ ∣ ′ = v ⃗ ∣ ∣ \vec{v}_{||}^{'}=\vec{v}_{||} v∣∣′=v∣∣
v ⃗ ⊥ \vec{v}_{\bot} v⊥的旋转
因为 v ⃗ ⊥ \vec{v}_{\bot} v⊥与 u ⃗ \vec{u} u的是正交的,这个旋转可以看做是平面内的一个旋转。因为旋转不改变 v ⃗ ⊥ \vec{v}_{\bot} v⊥的长度,所以旋转路径是一个圆。下面是这个旋转的示意图,右侧的为俯视图:
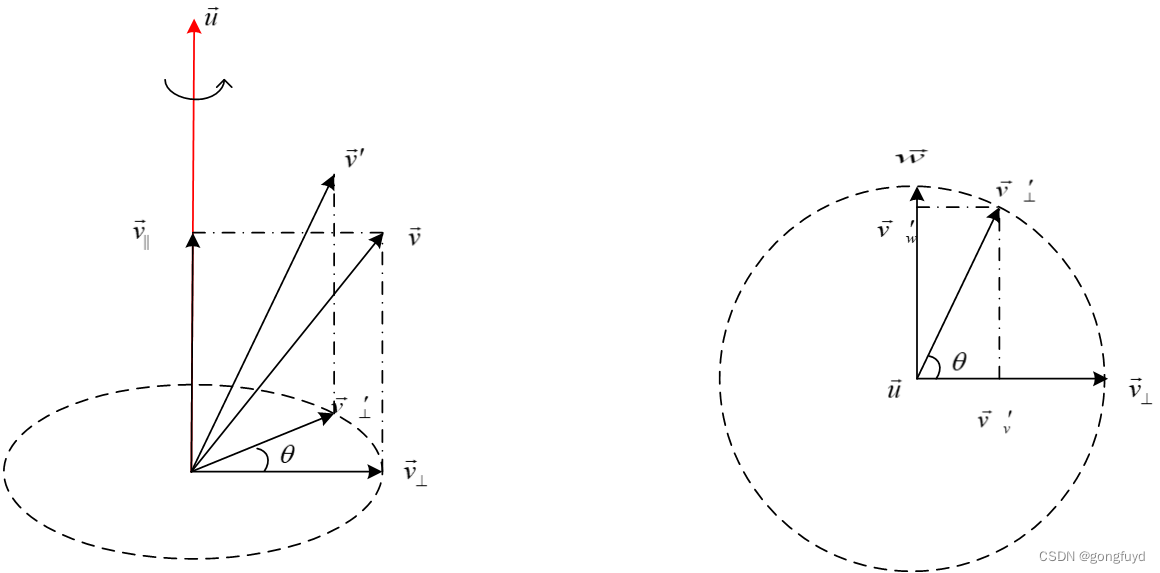
现在,3D 的旋转被转化为了 2D 平面上的旋转.由于在这个平面上们只有一个向量 v ⃗ ⊥ \vec{v}_{\bot} v⊥,用它来表示一个旋转是不够的,还需要构造一个同时正交于 u ⃗ \vec{u} u和 v ⃗ ⊥ \vec{v}_{\bot} v⊥的向量 w ⃗ \vec{w} w,这个可以通过叉乘来获得:
w ⃗ = u ⃗ × v ⃗ ⊥ \vec{w}=\vec{u}×\vec{v}_{\bot} w=u×v⊥
注意叉乘的顺序,因为使用的是右手坐标系统,按照右手定则可以发现这个新的向量 w ⃗ \vec{w} w指向 v ⃗ ⊥ \vec{v}_{\bot} v⊥逆时针旋转 𝜋/2 后的方向,并且和 v ⃗ ⊥ \vec{v}_{\bot} v⊥一样也处于正交于 u ⃗ \vec{u} u的平面内.因为 ∣ ∣ u ⃗ ∣ ∣ = 1 ||\vec{u}||=1 ∣∣u∣∣=1,可以发现 ∣ ∣ w ⃗ ∣ ∣ = ∣ ∣ u ⃗ × v ⃗ ⊥ ∣ ∣ = ∣ ∣ u ⃗ ∣ ∣ ⋅ ∣ ∣ v ⃗ ⊥ ∣ ∣ ⋅ s i n ( π / 2 ) = ∣ ∣ v ⃗ ⊥ ∣ ∣ ||\vec{w}||=||\vec{u}×\vec{v}_{\bot}||=||\vec{u}||\cdot||\vec{v}_{\bot}||\cdot sin(\pi/2)=||\vec{v}_{\bot}|| ∣∣w∣∣=∣∣u×v⊥∣∣=∣∣u∣∣⋅∣∣v⊥∣∣⋅sin(π/2)=∣∣v⊥∣∣
也就是说, w ⃗ \vec{w} w和 v ⃗ ⊥ \vec{v}_{\bot} v⊥的模长是相同的,所以, w ⃗ \vec{w} w也位于圆上.有了这个新的向量 w ⃗ \vec{w} w,就相当于在平面内有了两个坐标轴.我们现在可以把 v ⃗ ⊥ ′ \vec{v}_{\bot}^{'} v⊥′投影到 w ⃗ \vec{w} w和 v ⃗ ⊥ \vec{v}_{\bot} v⊥上,将其分解为 v ⃗ v ′ \vec{v}_{v}^{'} vv′和 v ⃗ w ′ \vec{v}_{w}^{'} vw′。使用三角学的知识就能得到: v ⃗ ⊥ ′ = v ⃗ v ′ + v ⃗ w ′ = c o s ( θ ) v ⃗ ⊥ + s i n ( θ ) w ⃗ = c o s ( θ ) v ⃗ ⊥ + s i n ( θ ) ( u ⃗ × v ⃗ ⊥ ) \vec{v}_{\bot}^{'}=\vec{v}_{v}^{'}+\vec{v}_{w}^{'}=cos(\theta)\vec{v}_{\bot}+sin(\theta)\vec{w}=cos(\theta)\vec{v}_{\bot}+sin(\theta)(\vec{u}×\vec{v}_{\bot}) v⊥′=vv′+vw′=cos(θ)v⊥+sin(θ)w=cos(θ)v⊥+sin(θ)(u×v⊥)
这也就完成了旋转的第二步,可以得到这样一个定理:
当 v ⃗ ⊥ \vec{v}_{\bot} v⊥正交于旋转轴 u ⃗ \vec{u} u时,旋转 θ 角度之后的 v ⃗ ⊥ ′ \vec{v}_{\bot}^{'} v⊥′为: v ⃗ ⊥ ′ = c o s ( θ ) v ⃗ ⊥ + s i n ( θ ) ( u ⃗ × v ⃗ ⊥ ) \vec{v}_{\bot}^{'}=cos(\theta)\vec{v}_{\bot}+sin(\theta)(\vec{u}×\vec{v}_{\bot}) v⊥′=cos(θ)v⊥+sin(θ)(u×v⊥)
v ⃗ \vec{v} v的旋转
将上面的两个结果组合就可以获得 v ⃗ ′ = v ⃗ ∣ ∣ ′ + v ⃗ ⊥ ′ = v ⃗ ∣ ∣ + c o s ( θ ) v ⃗ ⊥ + s i n ( θ ) ( u ⃗ × v ⃗ ⊥ ) \vec{v}^{'}=\vec{v}_{||}^{'}+\vec{v}_{\bot}^{'}=\vec{v}_{||}+cos(\theta)\vec{v}_{\bot}+sin(\theta)(\vec{u}×\vec{v}_{\bot}) v′=v∣∣′+v⊥′=v∣∣+cos(θ)v⊥+sin(θ)(u×v⊥)
因为叉乘遵守分配律,
u ⃗ × v ⃗ ⊥ = u ⃗ × ( v ⃗ − v ⃗ ∥ ∣ ) = u ⃗ × v ⃗ − u ⃗ × v ⃗ ∥ ∣ = u ⃗ × v ⃗ \vec{u}×\vec{v}_{\bot}= \vec{u}×(\vec{v}-\vec{v}_{\||})= \vec{u}×\vec{v}-\vec{u}×\vec{v}_{\||}= \vec{u}×\vec{v} u×v⊥=u×(v−v∥∣)=u×v−u×v∥∣=u×v
最后,将 v ⃗ ∣ ∣ = ( u ⃗ ⋅ v ⃗ ) u ⃗ \vec{v}_{||} = (\vec{u}\cdot\vec{v})\vec{u} v∣∣=(u⋅v)u与 v ⃗ ⊥ = v ⃗ − ( u ⃗ ⋅ v ⃗ ) u ⃗ \vec{v}_{\bot} =\vec{v}-(\vec{u}\cdot\vec{v})\vec{u} v⊥=v−(u⋅v)u代入 v ⃗ ′ = ( u ⃗ ⋅ v ⃗ ) u ⃗ + c o s ( θ ) ( v ⃗ − ( u ⃗ ⋅ v ⃗ ) u ⃗ ) + s i n ( θ ) ( u ⃗ × v ⃗ ) = c o s ( θ ) v ⃗ + ( 1 − c o s ( θ ) ) ( u ⃗ ⋅ v ⃗ ) u ⃗ + s i n ( θ ) ( u ⃗ × v ⃗ ) \vec{v}^{'}= (\vec{u}\cdot\vec{v})\vec{u}+cos(\theta)(\vec{v}-(\vec{u}\cdot\vec{v})\vec{u})+sin(\theta)(\vec{u}×\vec{v}) \\=cos(\theta)\vec{v}+(1-cos(\theta))(\vec{u}\cdot\vec{v})\vec{u}+sin(\theta)(\vec{u}×\vec{v}) v′=(u⋅v)u+cos(θ)(v−(u⋅v)u)+sin(θ)(u×v)=cos(θ)v+(1−cos(θ))(u⋅v)u+sin(θ)(u×v)
结论
3D 向量旋转公式(向量型,一般情况,也叫做「Rodrigues’ Rotation Formula」)
3D 空间中任意一个向量 v ⃗ \vec{v} v沿着单位向量 u ⃗ \vec{u} u旋转 θ 角度之后得到的向量 v ⃗ ′ \vec{v}^{'} v′为:
v ⃗ ′ = c o s ( θ ) v ⃗ + ( 1 − c o s ( θ ) ) ( u ⃗ ⋅ v ⃗ ) u ⃗ + s i n ( θ ) ( u ⃗ × v ⃗ ) \vec{v}^{'}=cos(\theta)\vec{v}+(1-cos(\theta))(\vec{u}\cdot\vec{v})\vec{u}+sin(\theta)(\vec{u}×\vec{v}) v′=cos(θ)v+(1−cos(θ))(u⋅v)u+sin(θ)(u×v)
致谢
本文主要参考https://github.com/Krasjet/quaternion
相关文章:

三维向量旋转
三维向量旋转 问题描述问题分析 v ⃗ ∣ ∣ \vec{v}_{||} v ∣∣的旋转 v ⃗ ⊥ \vec{v}_{\bot} v ⊥的旋转 v ⃗ \vec{v} v 的旋转结论致谢 问题描述 如图1所示,设一个向量 v ⃗ \vec{v} v 绕另一个向量 u ⃗ [ x , y , z ] T \vec{u}[x,y,z]^{T} u [x,y,z]T…...

顺序表——leetcode
原地删除数据 我们的思路这里给的是双指针,给两个指针,从前往后移动,如果不是val就覆盖,如果是我就跳过,大家一定要看到我们的条件是原地修改,所以我们不能另开一个数组来实现我们这道题目。 这里我们给两…...

Kaprekar 7641 - 1467= 6174
package homework;import java.util.Arrays;import util.StringUtil;/*** 数学黑洞数6174,即卡普雷卡尔(Kaprekar)常数, 它的算法如下: 取任意一个4位数(4个数字均为同一个数的除外)࿰…...
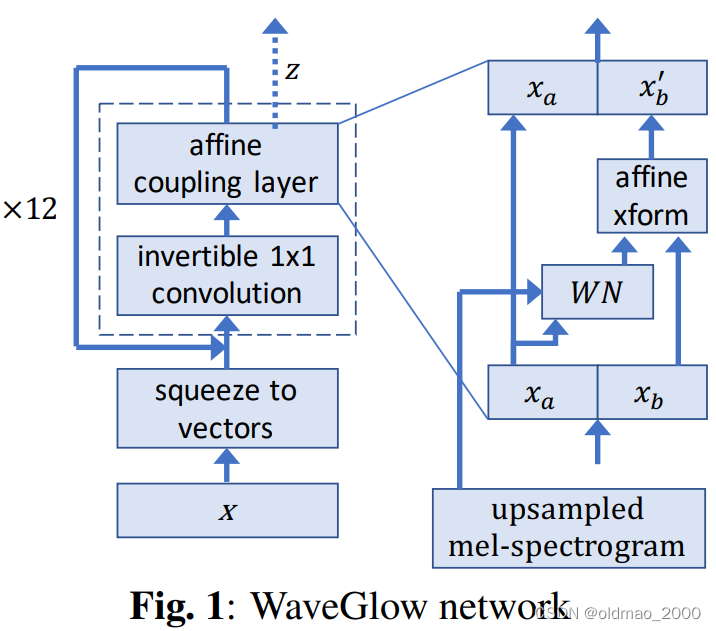
李宏毅机器学习笔记.Flow-based Generative Model(补)
文章目录 引子生成问题回顾:GeneratorMath BackgroundJacobian MatrixDeterminant 行列式Change of Variable Theorem简单实例一维实例二维实例 网络G的限制基于Flow的网络构架G的训练Coupling LayerCoupling Layer反函数计算Coupling Layer Jacobian矩阵计算Coupli…...

Java使用Spark入门级非常详细的总结
目录 Java使用Spark入门 环境准备 安装JDK 安装Spark 编写Spark应用程序 创建SparkContext 读取文本文件 计算单词出现次数 运行Spark应用程序 总结 Java使用Spark入门 本文将介绍如何使用Java编写Spark应用程序。Spark是一个快速的、通用的集群计算系统,它可以处理…...
kubernetes集群编排——k8s存储
configmap 字面值创建 kubectl create configmap my-config --from-literalkey1config1 --from-literalkey2config2kubectl get cmkubectl describe cm my-config 通过文件创建 kubectl create configmap my-config-2 --from-file/etc/resolv.confkubectl describe cm my-confi…...

【软件STM32cubeIDE下H73xx配置串口uart1+中断接收/DMA收发+HAL库+简单数据解析-基础样例】
#【软件STM32cubeIDE下H73xx配置串口uart1中断接收/DMA收发HAL库简单数据解析-基础样例】 1、前言2、实验器件3-1、普通收发中断接收实验第一步:代码调试-基本配置(1)基本配置(3)时钟配置(4)保存…...

jdk8和jdk9中接口的新特性
jdk8之前:声明抽象方法,修饰为public abstract。 jdk8:添加声明静态方法,默认方法。 jdk9:添加声明私有方法 jdk8: ①接口中声明的静态方法只能被接口来调用,不能使用其实现类进行调用 静态方法的声明&…...

1-爬虫-requests模块快速使用,携带请求参数,url 编码和解码,携带请求头,发送post请求,携带cookie,响应对象, 高级用法
1 爬虫介绍 2 requests模块快速使用 3 携带请求参数 4 url 编码和解码 4 携带请求头 5 发送post请求 6 携带cookie 7 响应对象 8 高级用法 1 爬虫介绍 # 爬虫是什么?-网页蜘蛛,网络机器人,spider-在互联网中 通过 程序 自动的抓取数据 的过程…...
java商城免费搭建 VR全景商城 saas商城 b2b2c商城 o2o商城 积分商城 秒杀商城 拼团商城 分销商城 短视频商城
1. 涉及平台 平台管理、商家端(PC端、手机端)、买家平台(H5/公众号、小程序、APP端(IOS/Android)、微服务平台(业务服务) 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、Redis 3. 前端框架…...
【TS篇一】TypeScript介绍、使用场景、环境搭建、类和接口
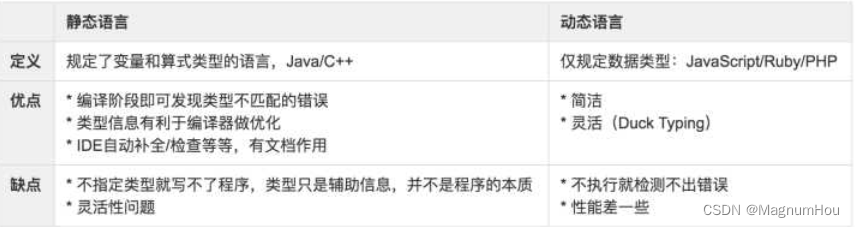
文章目录 一、TypeScript 介绍1. TypeScript 是什么1.2 静态类型和动态类型1.3 Why TypeScript1.4 TypeScript 使用场景1.5 TypeScript 不仅仅用于开发 Angular 应用1.6 前置知识 二、如何学习 TypeScript2.1 相关链接 三、起步3.1 搭建 TypeScript 开发环境3.2 编辑器的选择3.…...

Tuna: Instruction Tuning using Feedback from Large Language Models
本文是LLM系列文章,针对《Tuna: Instruction Tuning using Feedback from Large Language Models》的翻译。 Tuna:使用来自大型语言模型的反馈的指令调优 摘要1 引言2 方法3 实验4 相关工作5 结论局限性 摘要 使用更强大的LLM(如Instruction GPT和GPT-…...

uni-app 应对微信小程序最新隐私协议接口要求的处理方法
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 一,问题起因 最新在开发小程序的时候,调用微信小程序来获取用户信息的时候经常报错一个问题 fail api scope is not declared in the privacy agreement,api更具公告…...
PostgreSQL 进阶 - 使用foreign key,使用 subqueries 插入,inner joins,outer joins
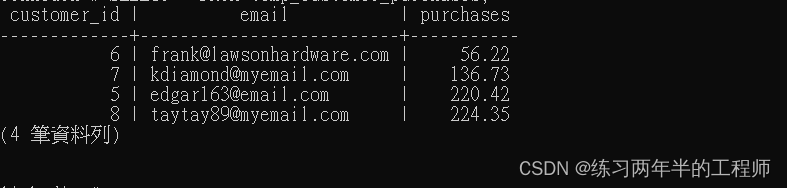
1. 使用foreign key 创建 table CREATE TABLE orders( order_id SERIAL PRIMARY KEY, purchase_total NUMERIC, timestamp TIMESTAMPTZ, customer_id INT REFERENCES customers(customer_id) ON DELETE CASCADE);“order_id”:作为主键的自增序列,使用 …...

【Python 千题 —— 基础篇】地板除计算
题目描述 题目描述 编写一个程序,接受用户输入的两个数字,然后计算这两个数字的地板除(整除)结果,并输出结果。 输入描述 输入两个数字,用回车隔开两个数字。 输出描述 程序将计算这两个数字的地板除…...
函数)
【随手记】np.random.choice()函数
np.random.choice() 是 NumPy 中的一个随机抽样函数,用于从给定的一维数组中随机抽取指定数量或指定概率的元素。该函数可以用于构建模拟实验、生成随机数据集、数据抽样等应用场景。 np.random.choice(a, sizeNone, replaceTrue, pNone) 的参数如下: …...
2003-2022年地级市-财政收支明细数据(企业、个人所得税、科学、教育、医疗等)
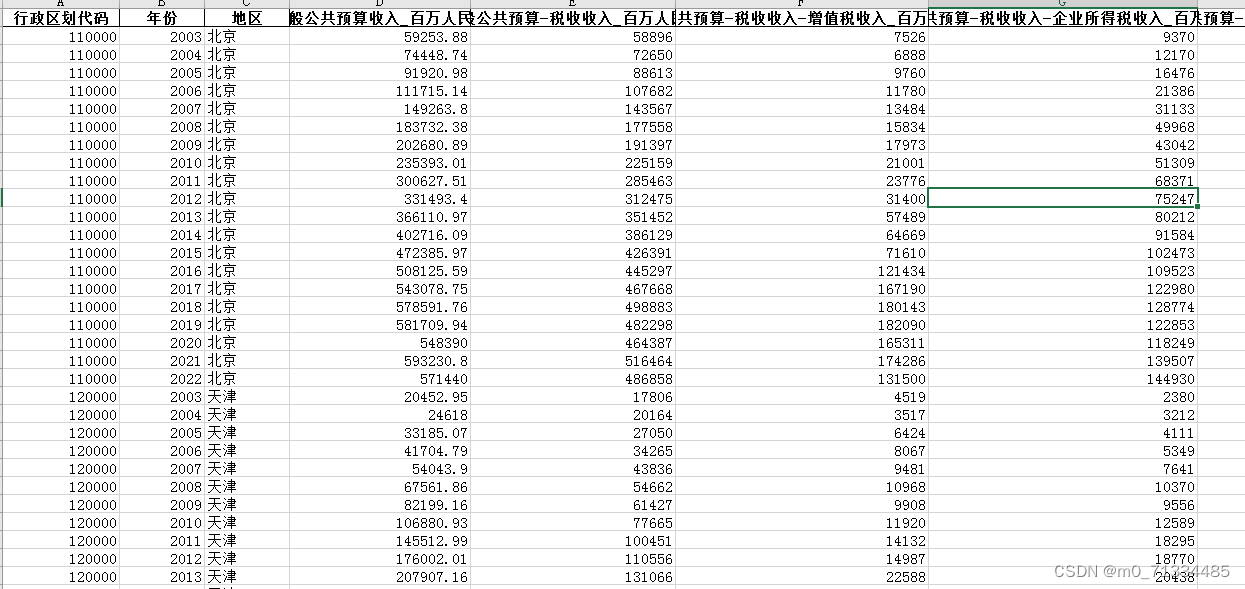
2003-2022年地级市-财政收支明细数据(企业、个人所得税、科学、教育、医疗等) 1、时间:2003-2022年 2、指标:行政区划代码、年份、地区、一般公共预算收入、一般公共预算-税收收入、一般公共预算-税收收入-增值税收入、一般公共…...

影响服务器正常使用的有哪些因素
对于网站优化来说,网站服务器的优化绝对是基础。不管是用户还是搜索引擎对于网站的打开速度都是没有太多耐心的, 所以网站优化的就是要保证网站服务器稳定,网站正常且快速的打开 1.用户体验较差 现在越来越强调用户体验,设想一下…...

NLP学习笔记:使用 Python 进行NLTK
一、说明 本文和接下来的几篇文章将介绍 Python NLTK 库。NLTK — 自然语言工具包 — NLTK 是一个强大的开源库,用于 NLP 的研究和开发。它内置了 50 多个文本语料库和词汇资源。它支持文本标记化、词性标记、词干提取、词形还原、命名实体提取、分割、分类、语义推…...

突破性技术!开源多模态模型—MiniGPT-5
多模态生成一直是OpenAI、微软、百度等科技巨头的重要研究领域,但如何实现连贯的文本和相关图像是一个棘手的难题。 为了突破技术瓶颈,加州大学圣克鲁斯分校研发了MiniGPT-5模型,并提出了全新技术概念“Generative Vokens ",…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
