算法通关村第六关-白银挑战树
大家好我是苏麟 , 今天聊聊树 .
大纲
- 树的概念
- 二叉树
- 满二叉树
- 完全二叉树
- 树的性质
- 树的定义与存储方式
- 树的遍历
- 通过序列构造二叉树
- 前中序列遍历
树的概念
树是我们计算机中非常重要的一种数据结构,同时使用树这种数据结构,可以描述现实生活中的很多事物,例如家谱、单位的组织架构、等等。
树是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
更好的理解 :
如企业里的职级关系 :
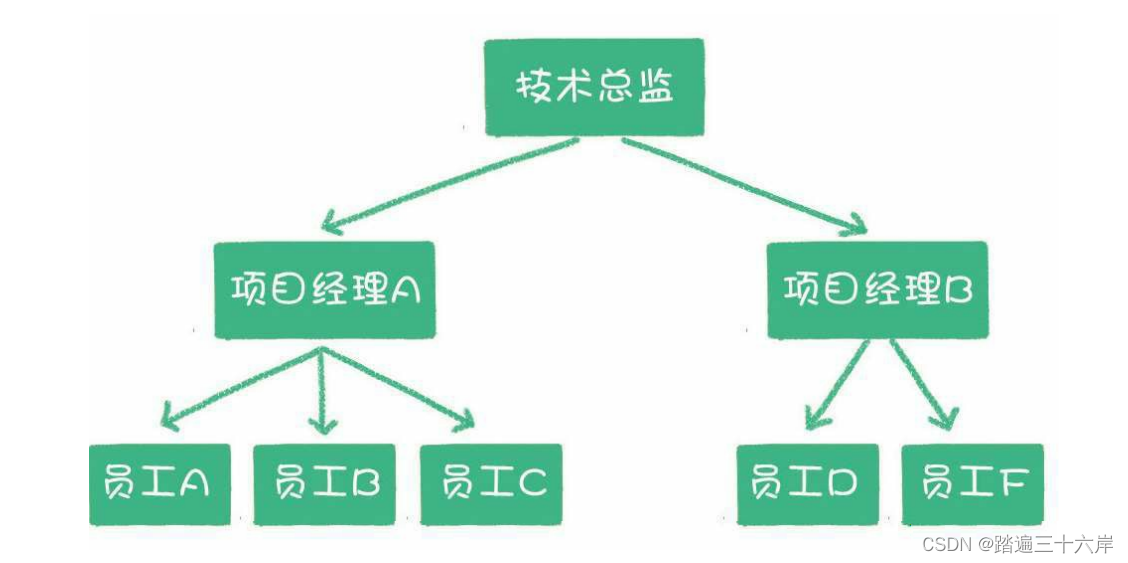
如一本书的目录 :
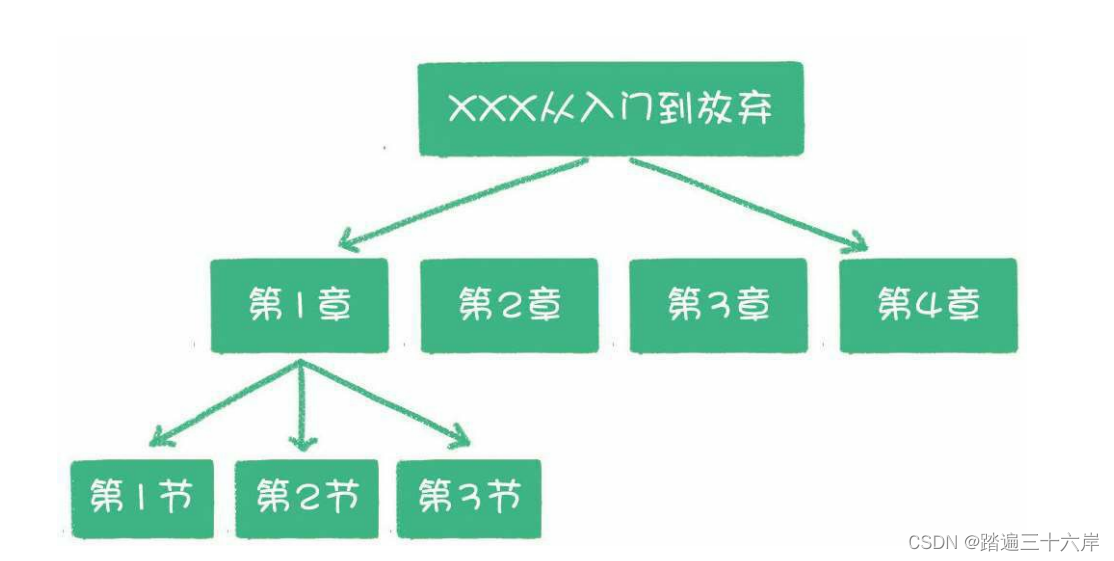
下面这张图,就是一个标准的树结构 :
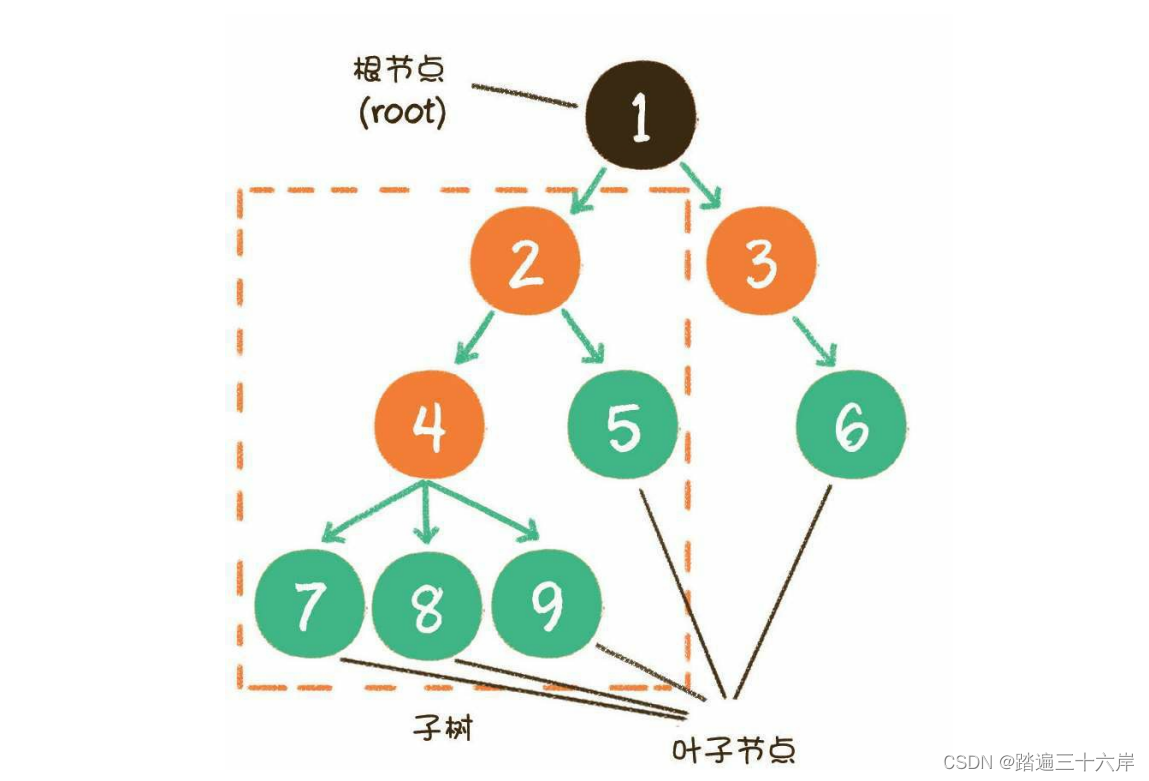
树具有以下特点:
1.每个结点有零个或多个子结点
2.没有父结点的结点为根结点
3.每一个非根结点只有一个父结点
4.每个结点及其后代结点整体上可以看做是一棵树,称为当前结点的父结点的一个子树
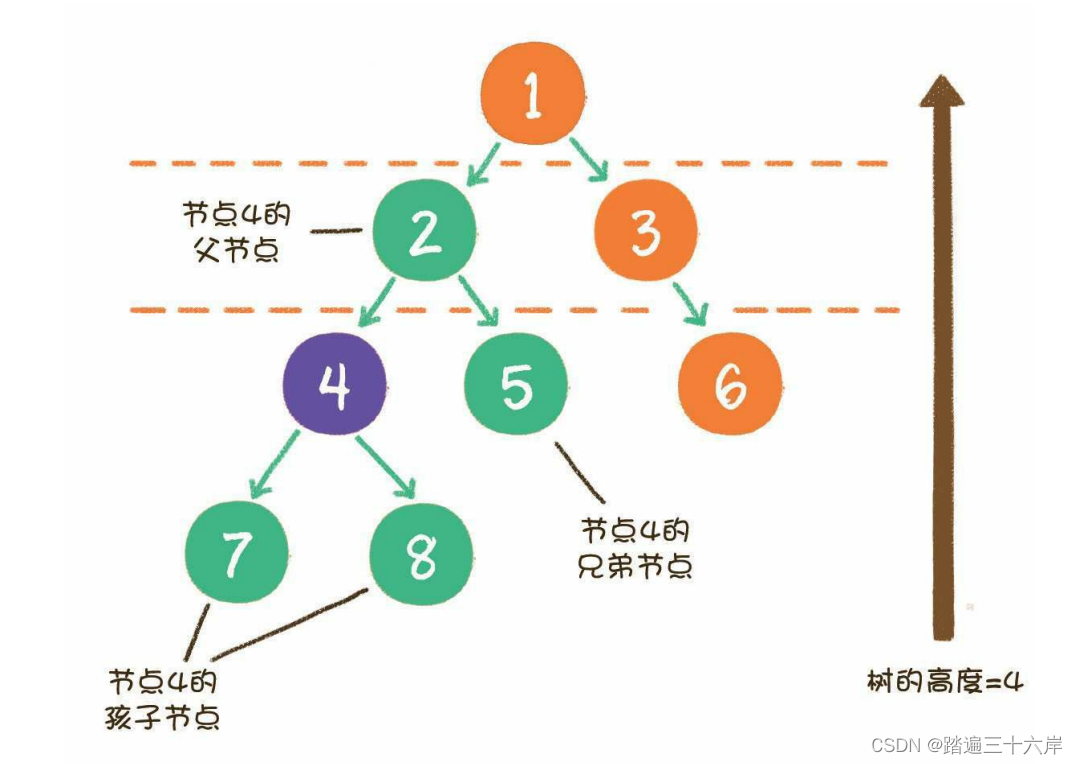
参考上面的结构,可以很方便的理解树的如下概念:
1.节点的度:一个节点含有的子节点的个数称为该节点的度
2.树的度:一棵树中,最大的节点的度称为树的度,注意与节点度的区别
3.叶节点或终端节点: 度为0的节点称为叶节点
4.非终端节点或分支节点:度不为0的节点
5.双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点
6.孩子节点或子节点: 一个节点含有的子树的根节点称为该节点的子节点
7.兄弟节点: 具有相同父节点的节点互称为兄弟节点
8.节点的祖先: 从根到该节点所经分支上的所有节点
9.子孙: 以某节点为根的子树中任一节点都称为该节点的子孙
10.森林: 由m(m>=0)棵互不相交的树的集合称为森林
11.无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树
12.有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树
13.二又树:每个节点最多含有两个子树的树称为二叉树
二叉树
二叉树(binary tree)是树的一种特殊形式。二叉,顾名思义,这种树的每个节点最多有2个孩子节点。注意,这里是最多有2个,也可能只有1个,或者没有孩子节点。
二叉树的结构如图所示 :
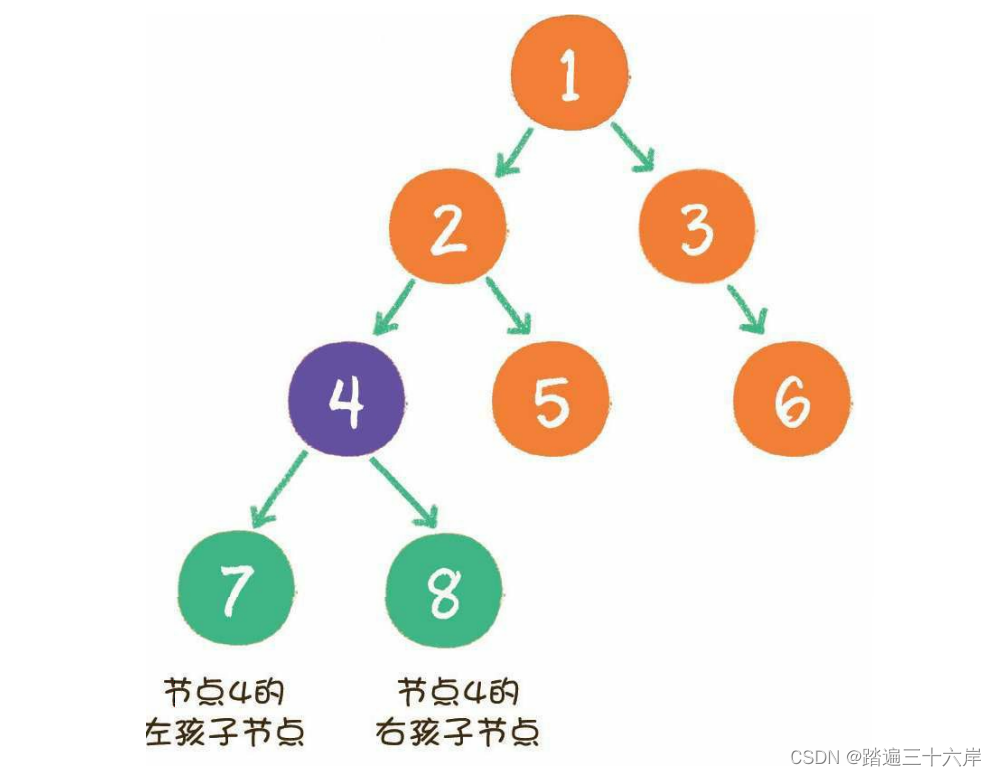
二叉树节点的两个孩子节点,一个被称为左孩子(left child),一个被称为右孩子(right child)。这两个孩子节点的顺序是固定的,就像人的左手就是左手,右手就是右手,不能够颠倒或混淆。
此外,二叉树还有两种特殊形式,一个叫作满二叉树,另一个叫作完全二叉树。
满二叉树
一个二叉树的所有非叶子节点都存在左右孩子,并且所有叶子节点都在同一层级上,那么这个树就是满二叉树。
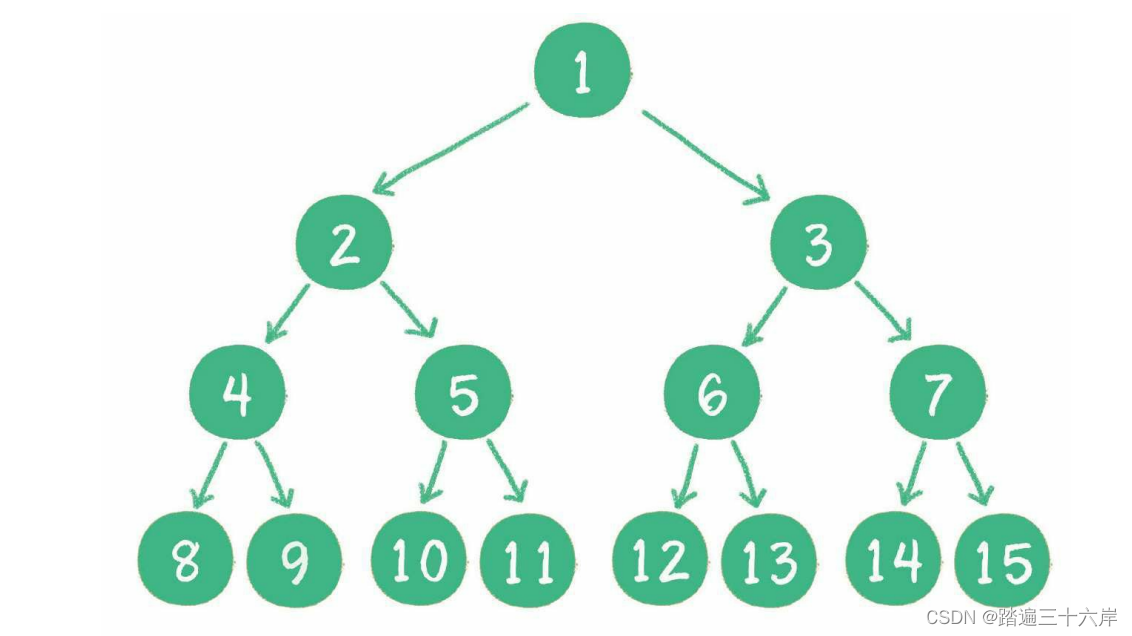
简单点说,满二叉树的每一个分支都是满的。
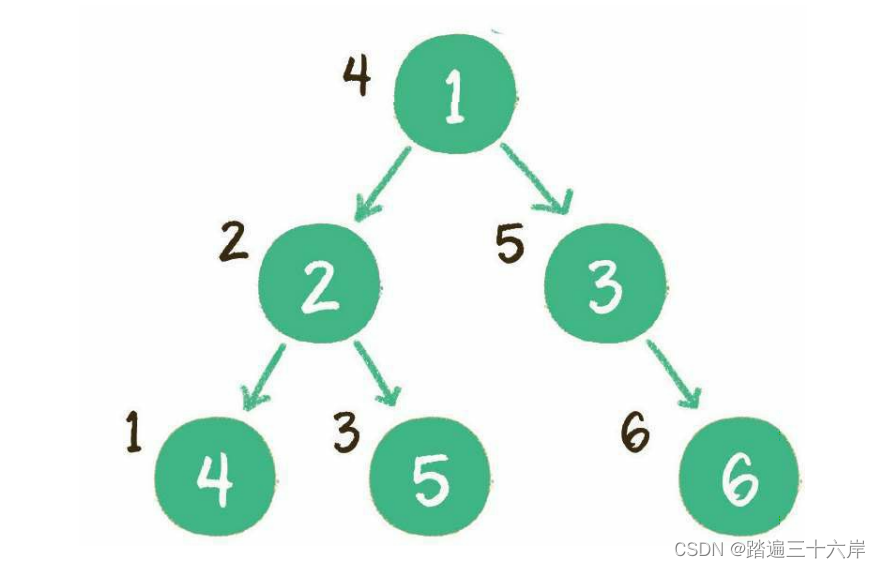
完全二叉树
对一个有n个节点的二叉树,按层级顺序编号,则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同,则这个二叉树为完全二叉树。
如图 :
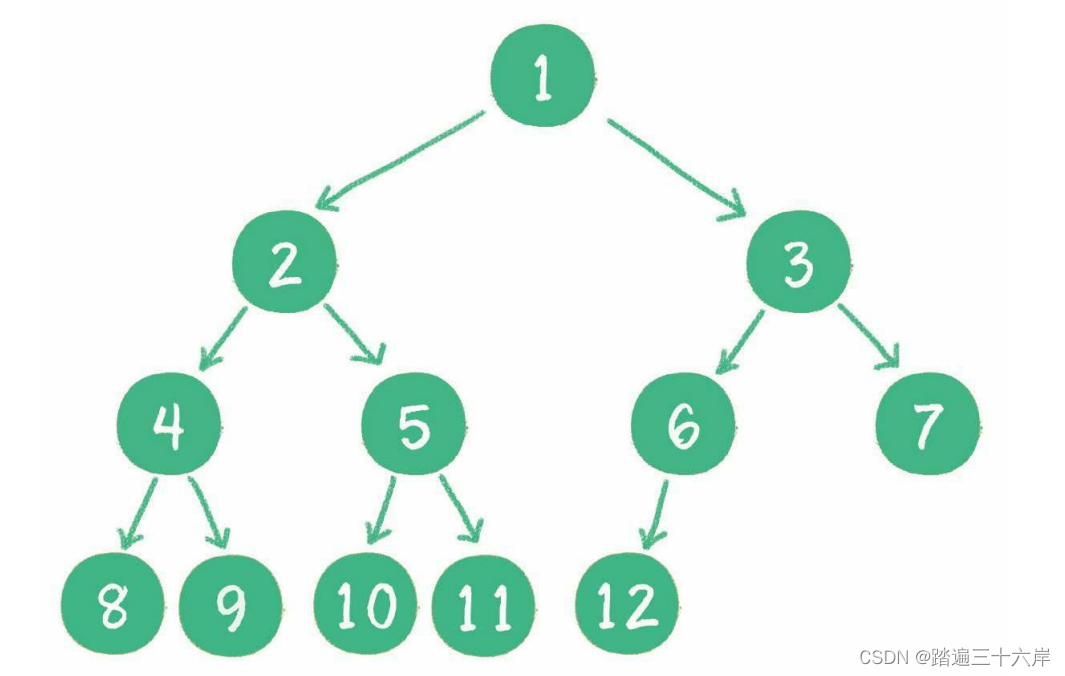
在上图中,二叉树编号从1到12的12个节点,和前面满二叉树编号从1到12的节点位置完全对应。因此这个树是完全二叉树。
完全二叉树的条件没有满二叉树那么苛刻:满二叉树要求所有分支都是满的;
而完全二叉树只需保证最后一个节点之前的节点都齐全即可。
树的性质
性质1: 在二又树的第i层上至多有2^(i-1)个结点 (i>0)
性质2: 深度为k的二又树至多有2^k - 1个结点 (k>0)
性质3: 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则NO=N2+1:
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
性质5:对完全二又树,若从上至下、从左至右编号,则编号为i 的结点,其左孩子编号必为2i.
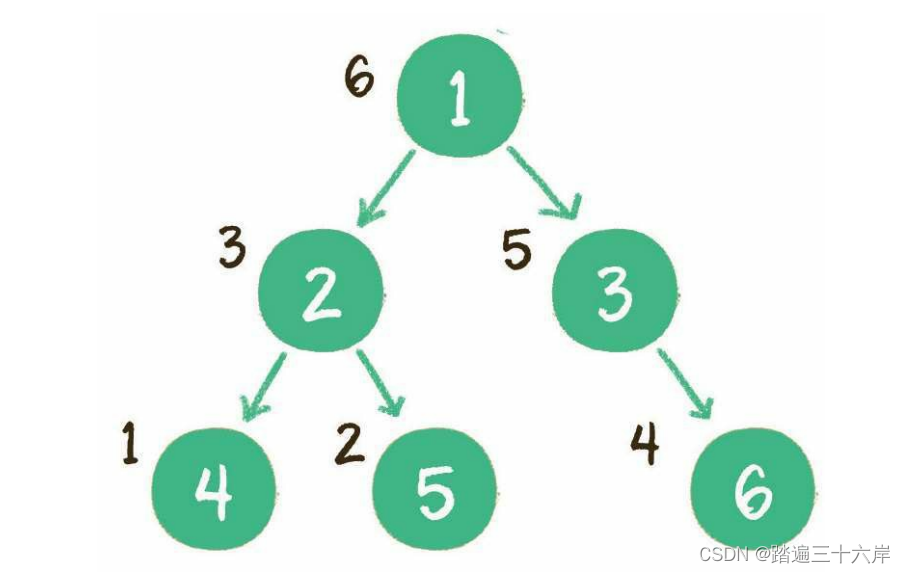
其右孩了编号必为2i+1;其双亲的编号必为i/2 (i= 1 时为根,除外)满二又树和完全二叉树是经常晕的问题,我们有必要单独看一下。满二又树就是如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二又树为满二叉树。
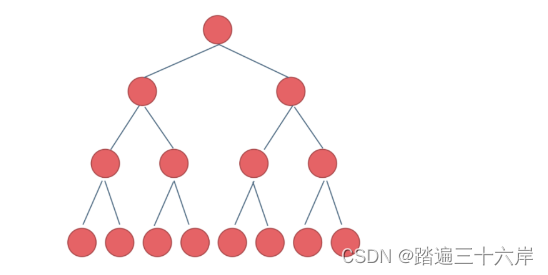
这棵二又树为满二又树,也可以说深度为k=4,有2^k-1=15个节点的二又树。完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大 值并且最下面一层的节点都集中在该层最左边的若千位置这个定义最邪乎了,估计大部分看了之后还是不懂什么是完全二叉树,看这个图就知道了:
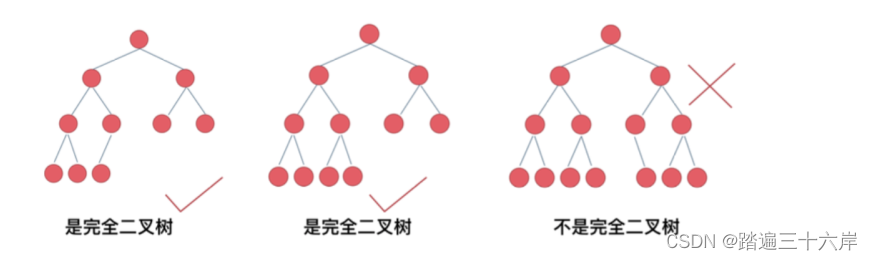
前面两棵树的前n-1层都是满的,最后一层所有节点都集中在左侧区域,而且节点之间不能有空隙。最后个为什么不是?因为有一节点缺了一个左子节点。
树的定义与存储方式
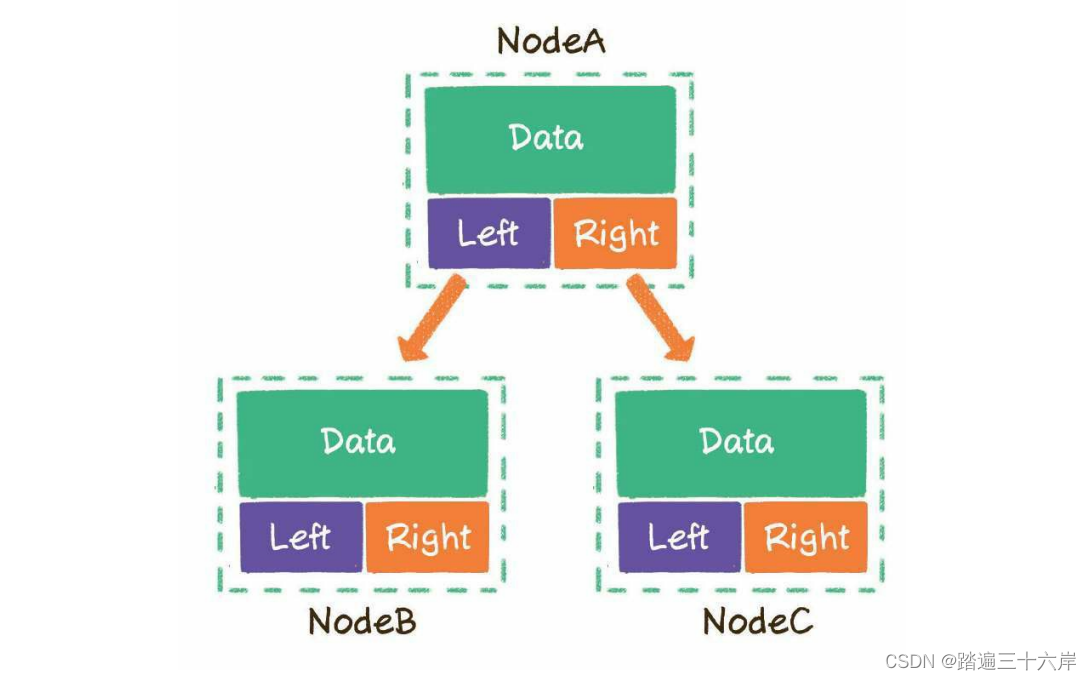
定义二叉树 : 一个节点最多可以指向左右两个孩子节点,所以二叉树的每一个节点包含3部分。
- 存储数据的data变量
- 指向左孩子的left指针
- 指向右孩子的right指针
public class Node{int value;Node left;Node right;
}
链式存储结构
数组存储
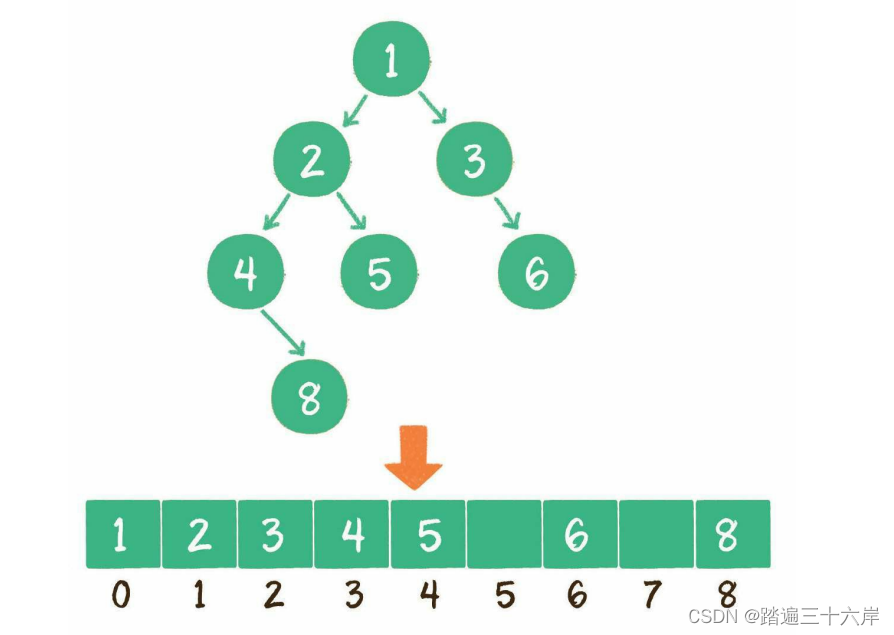
使用数组存储时,会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺,则数组的相应位置也空出来。
对于一个稀疏的二叉树来说,用数组表示法是非常浪费空间的。
树的遍历
二叉树的遍历分为4种 :
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
从更宏观的角度来看,二叉树的遍历归结为两大类 :
-
深度优先遍历(前序遍历、中序遍历、后序遍历)
-
广度优先遍历(层序遍历)
这两种遍历方式不仅仅是二叉树,N叉树也有这两种方式的,图结构也有,只不过我们更习惯叫广度优先和深度优先,本质是一回事。深度优先又有前中后序三种,有同学总分不清这三个顺序,问题就在不清楚这里前中后是相对谁来说的。记住一点:前指的是中间的父节点在遍历中的顺序,只要大家记住 前中后席指的就是中间节点的位置就可以了。
二叉树的前序遍历,输出顺序是根节点、左子树、右子树。
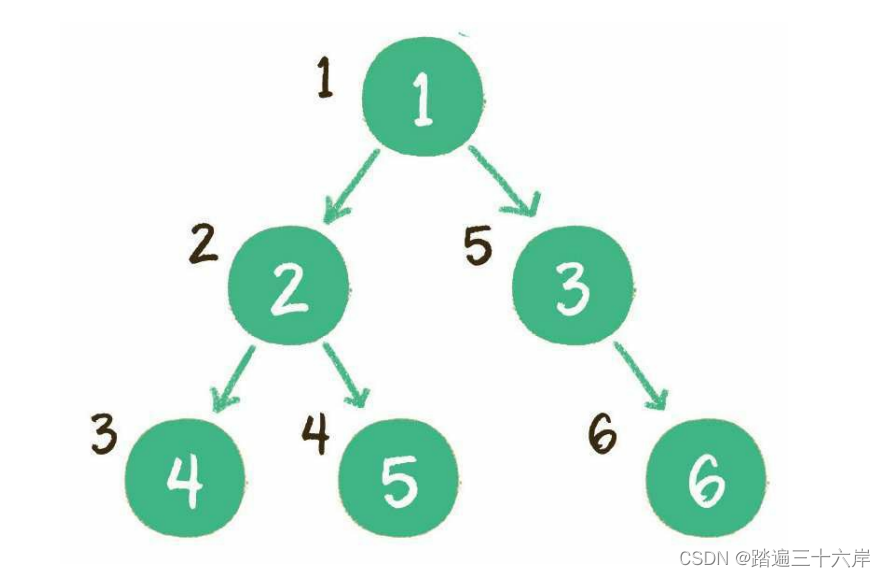
二叉树的中序遍历,输出顺序是左子树、根节点、右子树。
二叉树的后序遍历,输出顺序是左子树、右子树、根节点。
后面大量的算法都与这四种遍历方式有关,有的题目根据处理角度不同,可以用层次遍历,也可以用一种甚至两种深度优先的方式来实现。
通过序列构造二叉树
前面我们已经介绍了前中后序遍历的基本过程,现在我们看一下如何通过给出的序列来恢复原始二叉树看三个序列:
(1)前序: 1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2)中序: 3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
(3) 后序: 8 7 6 5 4 3 2 10 15 14 13 12 11 9 1
前中序列遍历
这期就到这里 , 下期再见!
相关文章:

算法通关村第六关-白银挑战树
大家好我是苏麟 , 今天聊聊树 . 大纲 树的概念二叉树满二叉树完全二叉树 树的性质树的定义与存储方式树的遍历通过序列构造二叉树前中序列遍历 树的概念 树是我们计算机中非常重要的一种数据结构,同时使用树这种数据结构,可以描述现实生活中的很多事物&…...
【Java对象】一文读懂 Java 对象庐山真面目及指针压缩
文章目录 版本及工具介绍Java 对象结构对象头mark word 标记字mark word 标记字解析Lock Record class point 类元数据指针 实例数据对齐填充为什么需要对齐填充 常见 Java 数据类型对象分析ArrayListLongStringByteBoolean 其它指针压缩前置知识:32位操作系统为什么…...

leetcode做题笔记210. 课程表 II
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。 例如,想要学习课程 0 ,你需要先完成课程 1…...
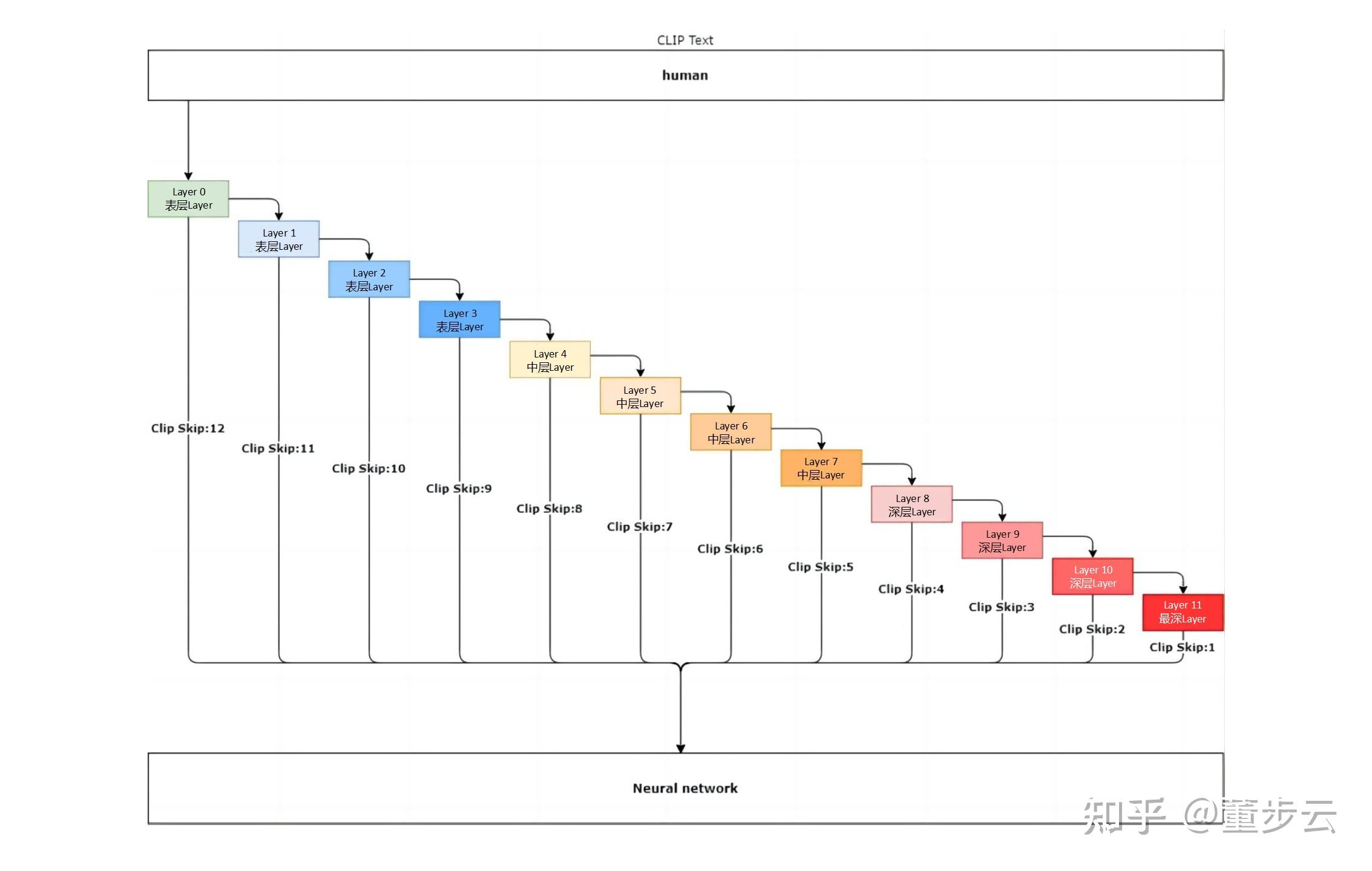
【深度学习 AIGC】stable diffusion webUI 使用过程,参数设置,教程,使用方法
文章目录 docker快速启动vae.ckpt或者.safetensorsCFG指数/CFG Scale面部修复/Restore facesRefinerTiled VAEClip Skipprompt提示词怎么写 docker快速启动 如果你想使用docker快速启动这个项目,你可以按下面这么操作(显卡支持CUDA11.8)。如…...
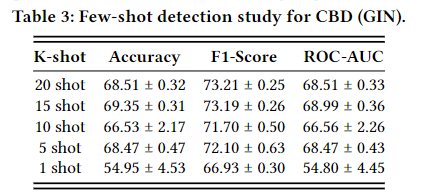
论文阅读 - Detecting Social Bot on the Fly using Contrastive Learning
目录 摘要: 引言 3 问题定义 4 CBD 4.1 框架概述 4.2 Model Learning 4.2.1 通过 GCL 进行模型预训练 4.2.2 通过一致性损失进行模型微调 4.3 在线检测 5 实验 5.1 实验设置 5.2 性能比较 5.5 少量检测研究 6 结论 https://dl.acm.org/doi/pdf/10.1145/358…...
)
PaddleMIX学习笔记(1)
写在前面 之前对HyperLedger的阅读没有完全结束,和很多朋友一样,同时也因为工作的需要,最近开始转向LLM方向。 国内在大模型方面生态做的最好的,目前还是百度的PaddlePaddle,所以自己也就先从PP开始看起了。 众所周知…...
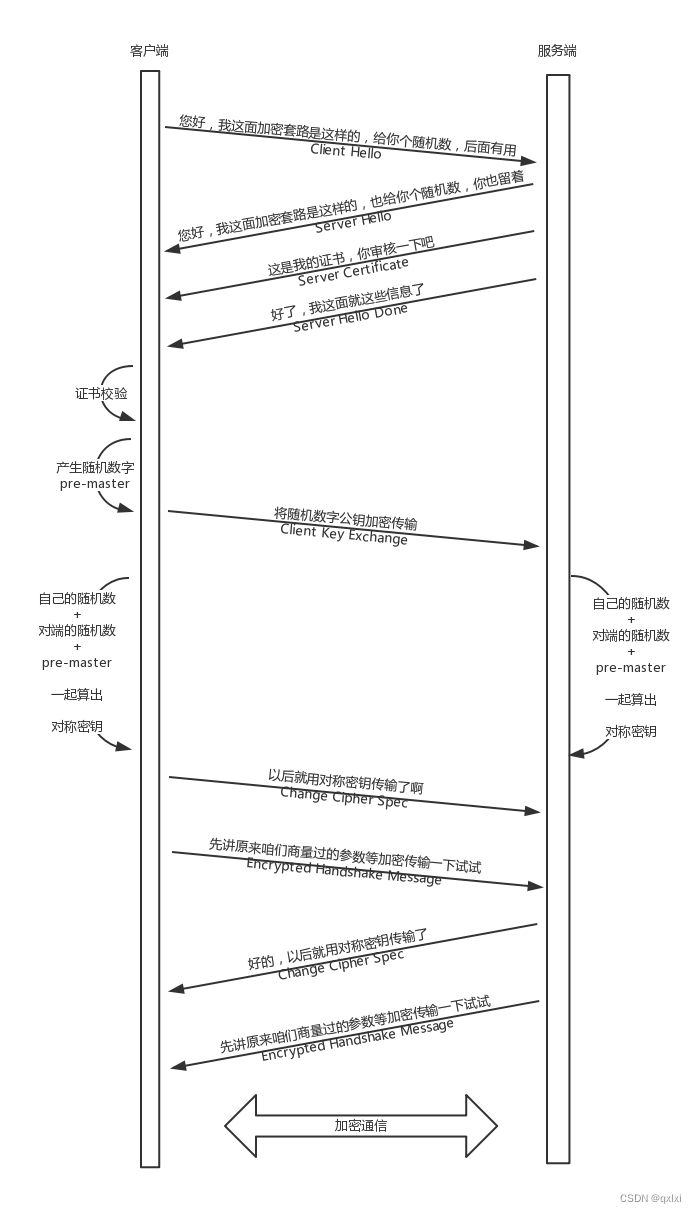
【网络协议】聊聊HTTPS协议
前面的文章,我们描述了网络是怎样进行传输数据包的,但是网络是不安全的,对于这种流量门户网站其实还好,对于支付类场景其实容易将数据泄漏,所以安全的方式是通过加密,加密方式主要是对称加密和非对称加密。…...

2023.11.2事件纪念
然而造化又常常为庸人设计,以时间的流逝,来洗涤旧迹,仅以留下淡红的血色和微漠的悲哀。 回顾这次事件,最深的感触就是什么是团队的力量! 当我们看到希望快要成功的时候,大家洋溢出兴奋开心的表情,一起的欢声笑语;但看…...

Scala和Play WS库编写的爬虫程序
使用Scala和Play WS库编写的爬虫程序,该程序将爬取网页内容: import play.api.libs.ws._ import scala.concurrent.ExecutionContext.Implicits.global object BaiduCrawler {def main(args: Array[String]): Unit {val url ""val proxy…...
佳易王配件进出库开单打印进销存管理系统软件下载
用版配件进出库开单打印系统,可以有效的管理:供货商信息,客户信息,进货入库打印,销售出库打印,进货明细或汇总统计查询,销售出库明细或汇总统计查询,库存查询,客户往来账…...
【深度学习基础】专业术语汇总(欠拟合和过拟合、泛化能力与迁移学习、调参和超参数、训练集、测试集和验证集)
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...
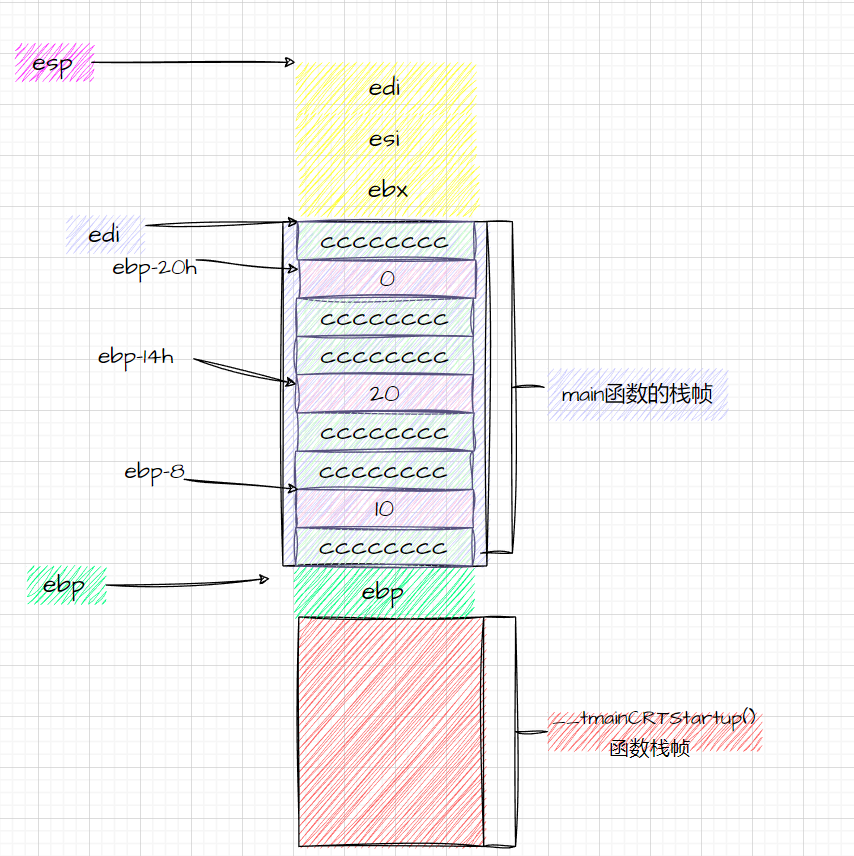
【C语言:函数栈帧的创建与销毁】
文章目录 前言一、前期准备1.寄存器2.汇编指令3.测试代码 二、解开函数栈帧的神秘面纱1.栈帧大体轮廓2.main函数栈帧的创建3.main函数内执行有效代码4.烫烫烫5.函数参数的传递6.add函数栈帧的创建7.add函数内执行有效代码8.add是如何获得参数的9. add函数栈帧的销毁10.main函数…...

怎么在C++中实现云端存储变量
随着云计算技术的快速发展,现在我们可以将数据存储在云端,以便于在不同设备和地点访问。在C中,我们也可以通过一些方法来实现这个功能。本文将详细介绍如何在C中实现云端存储变量。 首先,我们需要理解,C本身并没有直接…...

短视频矩阵营销系统工具如何助力商家企业获客?
1.批量剪辑技术研发 做的数学建模算法,数学阶乘的组合乘组形式,采用两套查重机制,一套针对素材进行查重抽帧素材,一套针对成片进行抽帧素材打分制度查重,自动滤重计入打分。 2.账号矩阵分发开发 多平台,…...

PCL 计算一个平面与包围盒体素的相交线
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 基于之前计算的包围盒体素(PCL 包围盒体素化显示),这里使用一个平面与其进行相交,并求出与其中体素单元的相交线。 二、实现代码 //标准文件 #include <iostream> #include <thread>//PCL...

面向教育的计算机视觉和深度学习5
面向教育的计算机视觉和深度学习5 1. 好处智能内容(Smart Content)任务自动化(Task Automation)缩小技能差距(Closing Skill Gap) 2. 应用程序学生学习与福利(Student Learning and Welfare&…...

FPGA芯片内部结构
参考链接:FPGA的进阶之第二章FPGA芯片内部结构(2)...
人工智能AI创作系统ChatGPT网站系统源码+AI绘画系统支持GPT4.0/支持Midjourney局部重绘
一、前言 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建…...

Google 开源项目风格指南
目录 C 风格指南 Objective-C 风格指南 Python 风格指南 Shell 风格指南 TypeScript 风格指南 Javascript 风格指南 HTML/CSS 风格指南 C 风格指南 C 风格指南 - 内容目录 — Google 开源项目风格指南 Objective-C 风格指南 Objective-C 风格指南 - 内容目录 — Googl…...

无限上下文,多级内存管理!突破ChatGPT等大语言模型上下文限制
目前,ChatGPT、Llama 2、文心一言等主流大语言模型,因技术架构的问题上下文输入一直受到限制,即便是Claude 最多只支持10万token输入,这对于解读上百页报告、书籍、论文来说非常不方便。 为了解决这一难题,加州伯克利…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...
