C++ 代码实例:多项式除法简单计算工具
文章目录
- 前言
- 代码仓库
- 代码
- 说明
- 核心片段
- 结果
- 总结
- 参考资料
- 作者的话
前言
C++ 代码实例:多项式除法简单计算工具。
代码仓库
- yezhening/Programming-examples: 编程实例 (github.com)
- Programming-examples: 编程实例 (gitee.com)
代码
说明
- 由于代码篇幅较多,在博客中直接粘贴并呈现会显得冗长,因此未在博客中放置完整代码,只展示核心片段代码。请前往"代码仓库"查看或获取相关代码
- 简单地计算多项式除法
- 注释有详细的步骤解析
- 好用的多项式除法在线计算网址:在线计算器: 多项式除法 (planetcalc.com)
- 多项式除法,被除数和除数写在程序中:main.exe、main.cpp、polynomial.cpp、polynomial.h
- 多项式除法,在终端输入被除数和除数:main1.exe、main1.cpp、polynomial.cpp、polynomial.h
注:一个晚上一个早上完成,应该大部分结果对,若出现小部分结果错误懒得管了,逻辑差不多那样
核心片段
polynomial.h
#ifndef POLYNOMIAL_H
#define POLYNOMIAL_H#include <vector>
#include <iostream>using std::ostream;
using std::vector;// 多项式类
class Polynomial
{
public:explicit Polynomial(const vector<int> &p) : poly_vec(p) {} // 私有成员只能在类的成员函数内部被初始化// 重载运算符 “<<” 输出多项式// friend:类外会用该运算符访问类的成员,不写报错:too many parameters for this operator function// 返回输出流对象引用,可以链式操作friend ostream &operator<<(ostream &output, const Polynomial &obj);// 重载运算符 “/” 进行多项式除法// 返回值:商// 参数:除数Polynomial operator/(const Polynomial &divisor) const; // const表示不会改变调用该方法的被除数// 重载运算符 “%” 进行多项式除法求余// 返回值:余数// 参数:除数// 照搬除法逻辑,只改动最后return的返回值,最后的余数就是最后更新的被除数Polynomial operator%(const Polynomial &divisor) const; // const表示不会改变调用该方法的被除数private:const vector<int> poly_vec; // 多项式的向量表示
};#endif // POLYNOMIAL_H
polynomial.cpp
// 重载运算符 “<<” 输出多项式
// 不需要friend、类作用域声名,因为是类外的运算符
ostream &operator<<(ostream &output, const Polynomial &obj)
{UINT terminal_code_page = GetConsoleOutputCP(); // 获取当前终端的输出代码页if (terminal_code_page != 65001){system("chcp 65001"); // 终端切换使用utf8字符集显示,以可以显示utf8的上标// 注意:会切换终端页,需要重新运行程序}else // 65001{}for (int i = obj.poly_vec.size() - 1; i >= 0; --i) // 从高位到低位 i既表示索引也表示次数{// 1. 系数的符号// 正数显示+,负数不显示-,系数负数已有-if (obj.poly_vec.at(i) >= 0){cout << "+";}else // obj.poly.at(i) < 0{// cout << " - ";}// 2. 系数cout << obj.poly_vec.at(i);// 3. 形式参数cout << "x";// 4. 次数// 上标号的utf8编码// 如:0上标号⁰的utf8编码在索引0为\u2070,1上标号¹的utf8编码在索引1为\u00B9,以此类推vector<string> superscript_utf8{"\u2070", "\u00B9", "\u00B2", "\u00B3", "\u2074", "\u2075", "\u2076", "\u2077", "\u2078", "\u2079"};cout << superscript_utf8.at(i);}return output;
}// 重载运算符 “/” 进行多项式除法
// 返回值:商
// 参数:除数
Polynomial Polynomial::operator/(const Polynomial &divisor) const // const表示不会改变调用该方法的被除数
{// 1. 准备被除数、除数和商// 解封装,获取被除数和除数向量// 1.1 方便操作// 1.2 不再是const,可以修改再封装出去vector<int> dividend_vec(this->poly_vec); // 被除数vector<int> divisor_vec(divisor.poly_vec); // 除数// 商初始的次数是被除数最高项次数 - 除数最高项次数 + 1// 如:// 4x³ + 3x² + 2x + 1,的个数是4,最高项次数次数是 4 - 1 = 3// x² + 2x + 1的个数是3,最高项次数次数是 3 - 1 = 2// 最高项相除,4x³ / x² = 4x,商的最高项次数是 3 - 2 = 1// 因为索引从0开始,所以需要+1,商系数的个数是1 + 1 = 2,初始化为0vector<int> quotient_vec((dividend_vec.size() - 1) - (divisor_vec.size() - 1) + 1, 0); // 商// 2. 除法运算// 2.1 如果被除数最高项次数 < 除数最高项次数,即 dividend_vec.size() - 1 < divisor_vec.size() - 1,商返回0// 如:4x³ + 3x² + 2x + 1 / x⁵ + 2x + 3,被除数最高项 4x³ 次数4 < 除数最高项 x⁵ 次数5,无法除,返回0(只有1个元素,索引0值0)if ((dividend_vec.size() - 1) < (divisor_vec.size() - 1)){quotient_vec.resize(1, 0);}// ...
}// 重载运算符 “%” 进行多项式除法求余
// 返回值:余数
// 参数:除数
// 照搬除法逻辑,只改动最后return的返回值,最后的余数就是最后更新的被除数
Polynomial Polynomial::operator%(const Polynomial &divisor) const // const表示不会改变调用该方法的被除数
{// ...
}
main.cpp
#include "polynomial.h"using std::cout;
using std::endl;int main()
{// int 型向量表示多项式,x作为形式参数无具体意义只有方便理解的展示意义,索引表示次数,值表示系数// 如 {1, 2},索引0值1表示1x⁰,索引1值2表示2x¹,所以多项式是:2x¹ + 1x⁰ = 2x + 1const vector<int> dividend_vec{1, 2, 3, 4}; // 被除数,4x³ + 3x² + 2x + 1const vector<int> divisor_vec{3,2,1}; // 除数,x² + 2x + 3// 多项式类表示多项式,进一步封装const Polynomial dividend(dividend_vec);const Polynomial divisor(divisor_vec);cout << "被除数: " << dividend << endl;cout << "除数: " << divisor << endl;// 多项式除法求商Polynomial quotient = dividend / divisor;cout << "商: " << quotient << endl;// 多项式除法求余数Polynomial remainder = dividend % divisor;cout << "余数: " << remainder << endl;return 0;
}
main1.cpp
#include <sstream> // istringstream#include "polynomial.h"using std::cin;
using std::cout;
using std::endl;
using std::getline;
using std::istringstream;
using std::string;int main()
{// 终端输入被除数和除数// int 型向量表示多项式,x作为形式参数无具体意义只有方便理解的展示意义,索引表示次数,值表示系数// 如 {1, 2},索引0值1表示1x⁰,索引1值2表示2x¹,所以多项式是:2x¹ + 1x⁰ = 2x + 1// 1. 被除数vector<int> dividend_vec(0);cout << "被除数系数,从高到低位输入,空格分隔,回车结束: " << endl;string input("");getline(cin, input); // 从终端获取一行输入istringstream iss(input); // 字符串 -> 输入流对象int num(0);while (iss >> num) // 输入流对象 -> 数字{dividend_vec.insert(dividend_vec.begin(), num); // 从后往前插入}// 2. 除数vector<int> divisor_vec(0);cout << "除数系数,从高到低位输入,空格分隔,回车结束: " << endl;input = "";getline(cin, input);iss.clear(); // 清楚流状态,否则获取不到数字iss.str(input);num = 0;while (iss >> num){divisor_vec.insert(divisor_vec.begin(), num);}// 多项式类表示多项式,进一步封装const Polynomial dividend(dividend_vec);const Polynomial divisor(divisor_vec);cout << "被除数: " << dividend << endl;cout << "除数: " << divisor << endl;// 多项式除法求商Polynomial quotient = dividend / divisor;cout << "商: " << quotient << endl;// 多项式除法求余数Polynomial remainder = dividend % divisor;cout << "余数: " << remainder << endl;return 0;
}
Makefile
.PHONY : all
all : main.exe main1.exemain.exe : main.cpp polynomial.cppg++ -o $@ $^main1.exe : main1.cpp polynomial.cppg++ -o $@ $^.PHONY : clean
clean :del *.exe
结果

总结
C++ 代码实例:多项式除法简单计算工具。
参考资料
- 无特定的参考资料
作者的话
- 感谢参考资料的作者/博主
- 作者:夜悊
- 版权所有,转载请注明出处,谢谢~
- 如果文章对你有帮助,请点个赞或加个粉丝吧,你的支持就是作者的动力~
- 文章在描述时有疑惑的地方,请留言,定会一一耐心讨论、解答
- 文章在认识上有错误的地方, 敬请批评指正
- 望读者们都能有所收获
相关文章:

C++ 代码实例:多项式除法简单计算工具
文章目录 前言代码仓库代码说明核心片段 结果总结参考资料作者的话 前言 C 代码实例:多项式除法简单计算工具。 代码仓库 yezhening/Programming-examples: 编程实例 (github.com)Programming-examples: 编程实例 (gitee.com) 代码 说明 由于代码篇幅较多&#…...

MySql表自修改报错:You can‘t specify target table ‘student‘ for update in FROM clause
文章目录 一、发现问题二、场景1:在where条件中查询了修改表的数据三、场景2:在set语句中查询了修改表的数据 一、发现问题 在一次准备处理历史数据sql时,出现这么一个问题:You cant specify target table 表名 for update in FR…...
LeetCode 热题100——链表专题
一、俩数相加 2.俩数相加(题目链接) 思路:这题题目首先要看懂,以示例1为例 即 342465807,而产生的新链表为7->0->8. 可以看成简单的从左向右,低位到高位的加法运算,4610,逢…...

植物花粉深度学习图片数据集大合集
最近收集了一波有关于植物花粉的图片数据集,可以用于相关深度学习模型的搭建,废话不多说,上数据集!!! 1、23种花粉类型805张花粉图像数据集 关于此数据:花粉种类和类型的分类是法医抱粉学、考…...
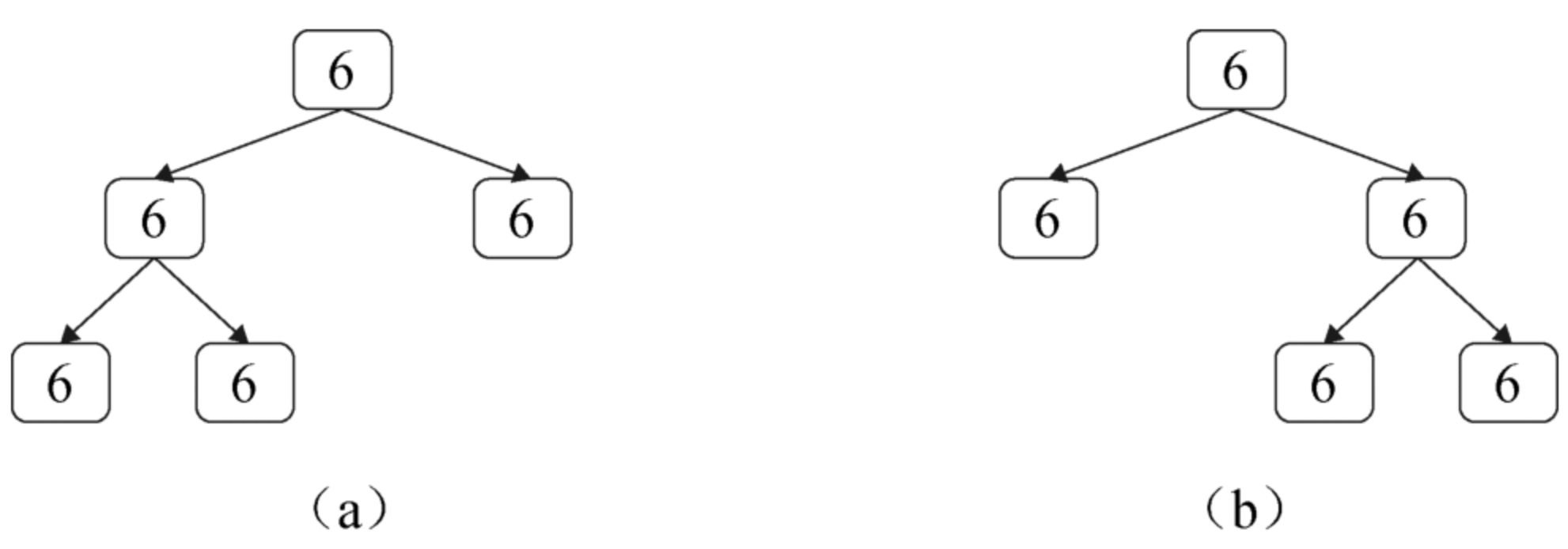
面试算法48:序列化和反序列化二叉树
题目 请设计一个算法将二叉树序列化成一个字符串,并能将该字符串反序列化出原来二叉树的算法。 分析 先考虑如何将二叉树序列化为一个字符串。需要逐个遍历二叉树的每个节点,每遍历到一个节点就将节点的值序列化到字符串中。以前序遍历的顺序遍历二叉…...
【Python基础】Python编程入门自学笔记,基础大全,一篇到底!
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...
windows自动登陆
新建文本粘贴下面代码,另存为注册表文件 Windows Registry Editor Version 5.00[HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Driver Signing] "Policy"hex:00[HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows NT\CurrentVersion\Winlogon]"DefaultUserN…...

5G及其后的5G非地面网络:趋势和研究挑战-HARQ部分
NTN组件纳入5G架构第一步 在NTN SI中定义了一组架构选项。就NT部分而言,已确定了两大类:星载(即基于卫星的通信平台)和机载(即HAPS)设备 并行管理HARQ最大进程数 NHARQRTT(NTX−1)2μ NTX:传输…...

【WPF系列】- XAML语法规范
【WPF系列】- XAML语法规范 文章目录 【WPF系列】- XAML语法规范一、概述二、对象元素语法三、特性语法(属性)四、特性值的处理五、枚举特性值六、属性和事件成员名称引用七、属性元素语法八、集合语法九、XAML 内容属性XAML 内容属性值必须是连续的 十、…...

antv/g6之图布局及切换布局
一般图布局 目前为止,g6的一般图布局已经有13种了,如下: Random Layout:随机布局;Force2 Layout:G6 4.7.0 后支持力导向布局,与 gForce 相比性能更强;GForce Layout:G6 4.0 支持的…...

Wordpress plugin removes ‘/category‘
plugin removes /category from your category permalinks Remove Category URL – WordPress plugin | WordPress.org...
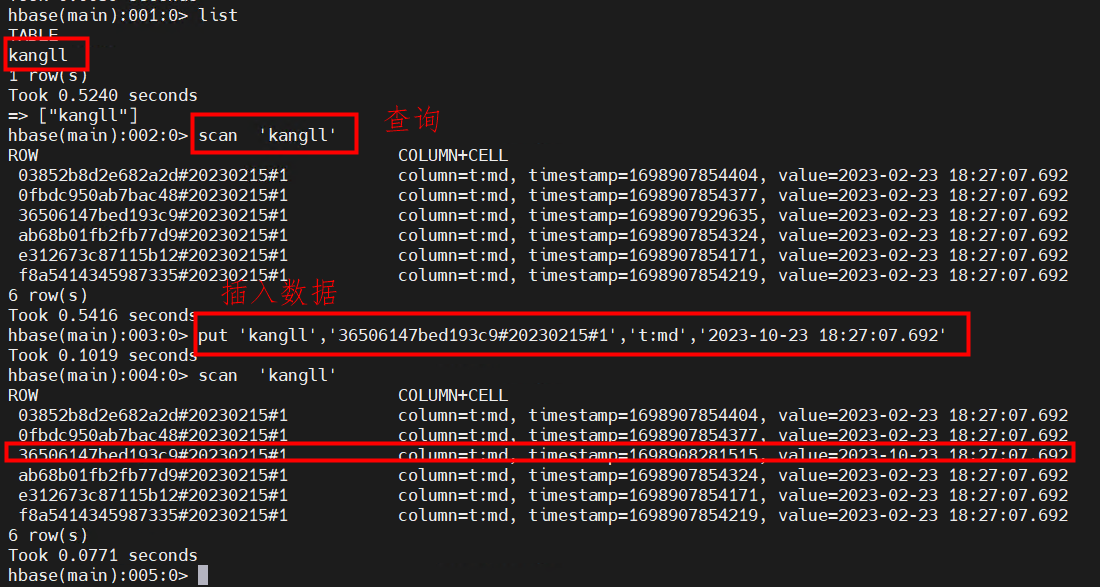
【大数据基础平台】星环TDH社区集群版本部署
🦄 个人主页——🎐开着拖拉机回家_大数据运维-CSDN博客 🎐✨🍁 🪁🍁🪁🍁🪁🍁🪁🍁 🪁🍁🪁…...
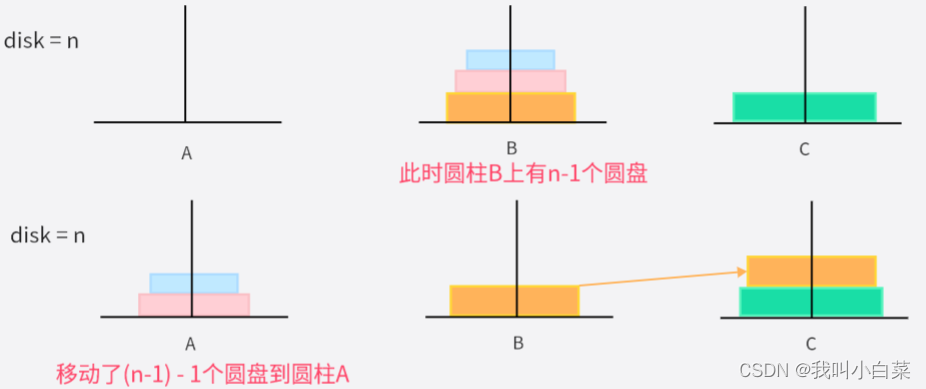
【Java】汉诺塔
汉诺塔 汉诺塔(Tower of Hanoi)(河内塔):把圆盘从下面开始按大小顺序重新摆放到另一根柱子上,并且小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。 汉诺塔规则 disk表示圆盘数一次只…...
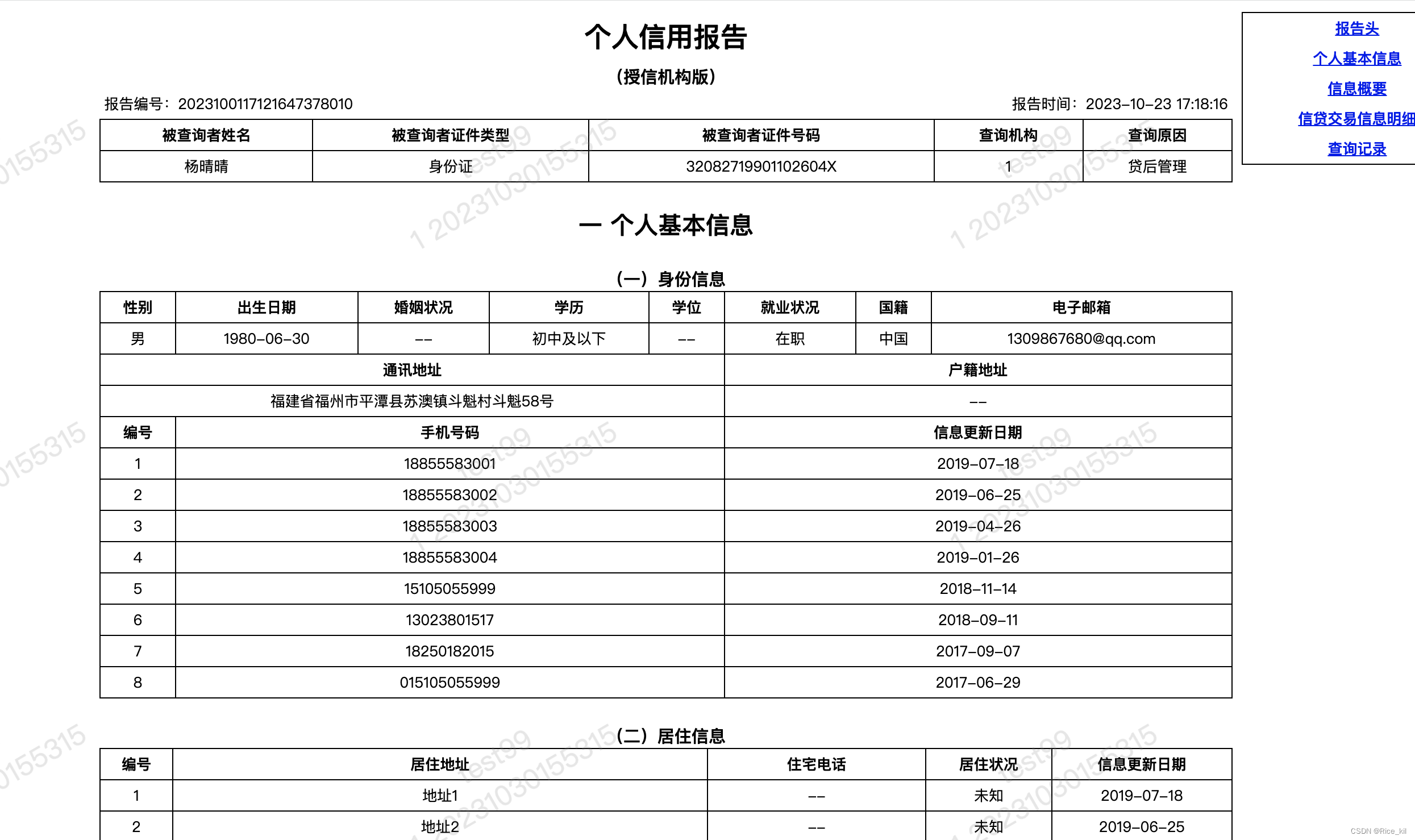
Java实现对Html文本的处理
1.引入jsoup <dependency><groupId>org.jsoup</groupId><artifactId>jsoup</artifactId><version>1.8.3</version> </dependency> 2. html示例 示例代码: <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1…...

Vue项目创建与启动(2023超详细的图文教程)
目录 一、下载node.js 二、下载vue-cli与webpack插件 三、项目初始化(项目配置详细信息) 四、项目启动 五、Vue项目工程结构(扩展知识) 一、下载node.js 1.检测是否已经安装过node.js 打开控制台,输入 npm -v如果有会显示对应版本 如果没有会显示…...
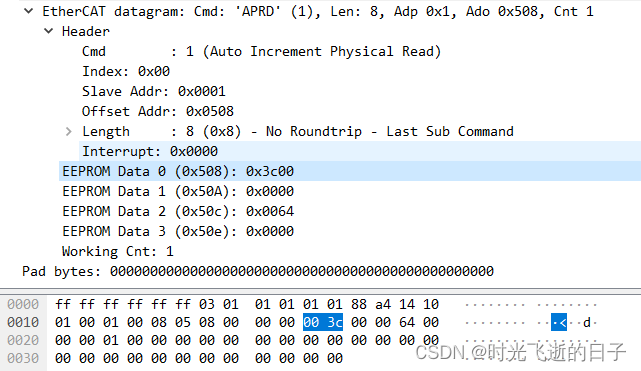
EtherCAT主站读取从站EEPROM抓包分析
0 工具准备 1.EtherCAT主站 2.EtherCAT从站(本文使用步进电机驱动器) 3.Wireshark1 抓包分析 1.1 报文总览 本文让主站去读取从站1字地址为0的EEPROM数据内容,主站读取从站EEPROM数据内容使用Wireshark抓包如下: 1.2 EEPROM读…...

Elasticsearch 8.X 如何生成 TB 级的测试数据 ?
1、实战问题 我只想插入大量的测试数据,不是想测试性能,有没有自动办法生成TB级别的测试数据?有工具?还是说有测试数据集之类的东西?——问题来源于 Elasticsearch 中文社区https://elasticsearch.cn/question/13129 2…...
汽车标定技术(四)--问题分析:多周期测量时上位机显示异常
目录 1.问题现象 2.数据流分析 3.代码分析 3.1 AllocDAQ 3.2 AllocOdt 3.3 AllocOdtEntry 4.根因分析及解决方法 4.1 根因分析 4.2 解决方案 1.问题现象 在手撸XCP代码时, DAQ的实现是一大头痛的事情。最初单周期实现还好一点,特别是…...
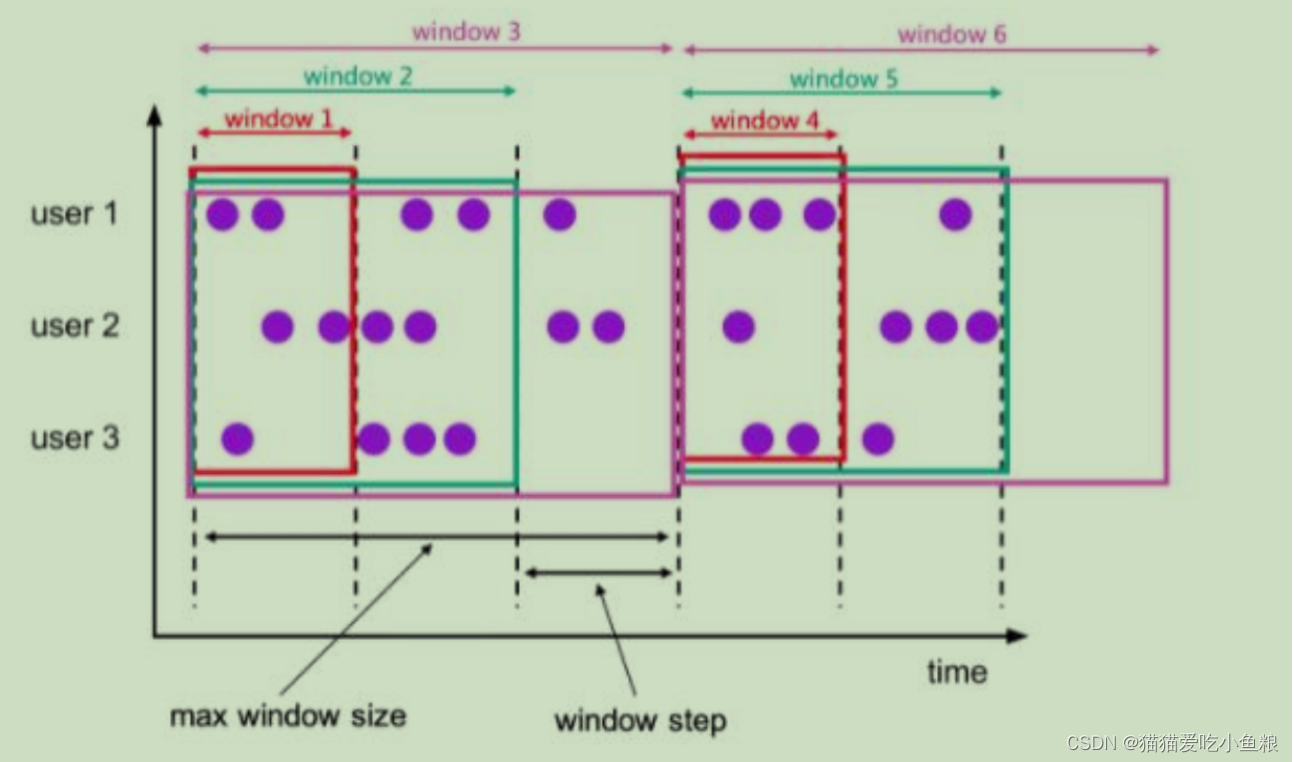
Flink SQL时间属性和窗口介绍
(1)概述 时间属性(time attributes),其实就是每个表模式结构(schema)的一部分。它可以在创建表的 DDL 里直接定义为一个字段,也可以在 DataStream 转换成表时定义。 一旦定义了时间…...
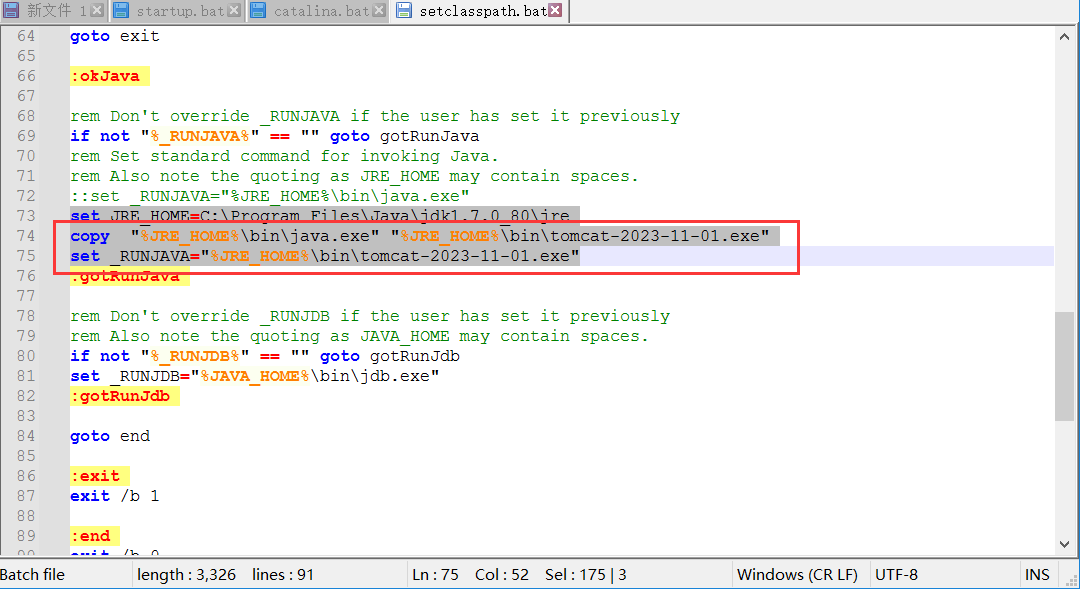
Tomcat免安装版修改标题名称和进程
tomcat免安装版启动后闪退问题 问题描述 在官网下载的tomcat免安装版的你安装完环境后发现启动闪退,tomcat启动依赖环境是JDK,所以需要tomcat对应版本的JDK支持。 tomcat8官网下载地址:https://tomcat.apache.org/ JDK环境官网下载地址&…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
