spring-session-core排除某些接口不设置session
这里写自定义目录标题
- 需求
- 实现
需求
今天先写一下如何实现,之后再更新一篇如何发现这个问题的。
我们的项目使用了spring-session-core来存储共享session,存在redis中,然后在cookie中是设置了key为SESSION的session。但是我们有一些开放接口不需要经过这一套来鉴权,所以需要排除这些接口,不设置session。
实现
实现主要分两步,第一步继承CookieHttpSessionIdResolver ,然后把排除条件加进去
public class CustomCookieSerializer extends CookieHttpSessionIdResolver {@Overridepublic void writeCookieValue(..) {if (needWriteCookie) { //判断条件根据自己的需求写super.writeCookieValue(..); }}}
第二步提供一个cookieSerializer来替代默认的
@Beanpublic CookieSerializer cookieSerializer() {CustomCookieSerializer serializer = new CustomCookieSerializer ();serializer.setCookieName("GULISESSION");serializer.setCookiePath("/");// 设置cookie的作用域为父域名return serializer;}
这样就可以了。
相关文章:

spring-session-core排除某些接口不设置session
这里写自定义目录标题 需求实现 需求 今天先写一下如何实现,之后再更新一篇如何发现这个问题的。 我们的项目使用了spring-session-core来存储共享session,存在redis中,然后在cookie中是设置了key为SESSION的session。但是我们有一些开放接口…...
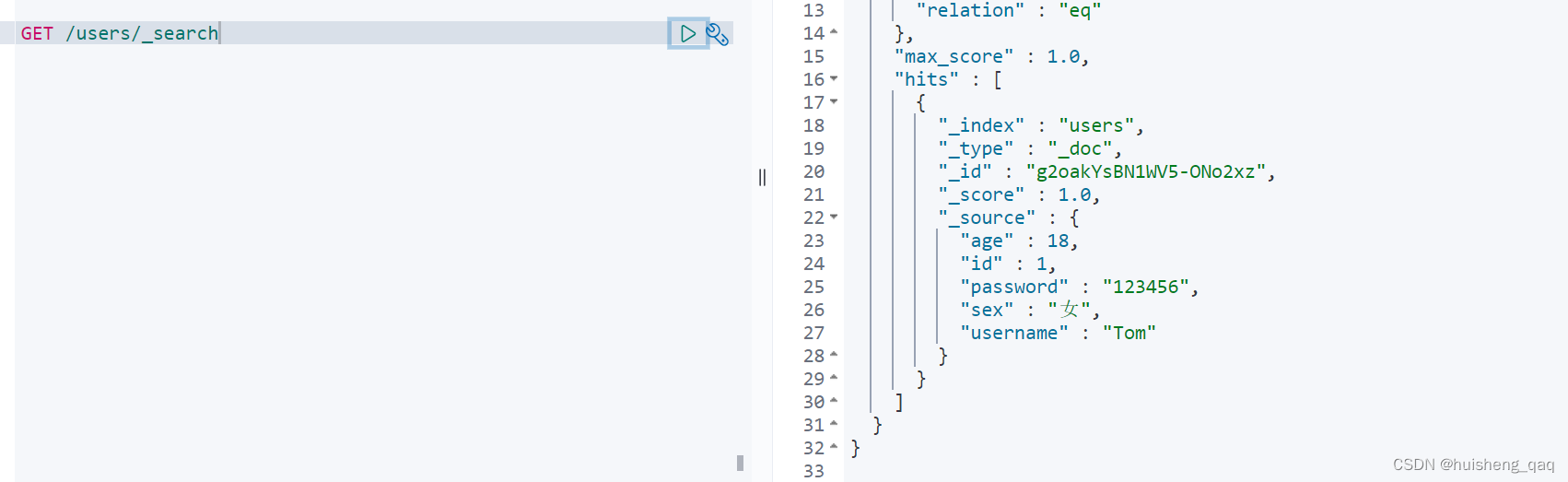
【ElasticSearch系列-05】SpringBoot整合elasticSearch
ElasticSearch系列整体栏目 内容链接地址【一】ElasticSearch下载和安装https://zhenghuisheng.blog.csdn.net/article/details/129260827【二】ElasticSearch概念和基本操作https://blog.csdn.net/zhenghuishengq/article/details/134121631【三】ElasticSearch的高级查询Quer…...

C/S架构学习之广播
广播:一台主机可以将一个数据包同时发送给同一局域网内所有主机;在IPV4中,广播地址是本网段最大的IP地址或者“255.255.255.255”;注意:广播本质上是UDP通信技术;只有用户数据报套接字才能使用广播的方式&a…...
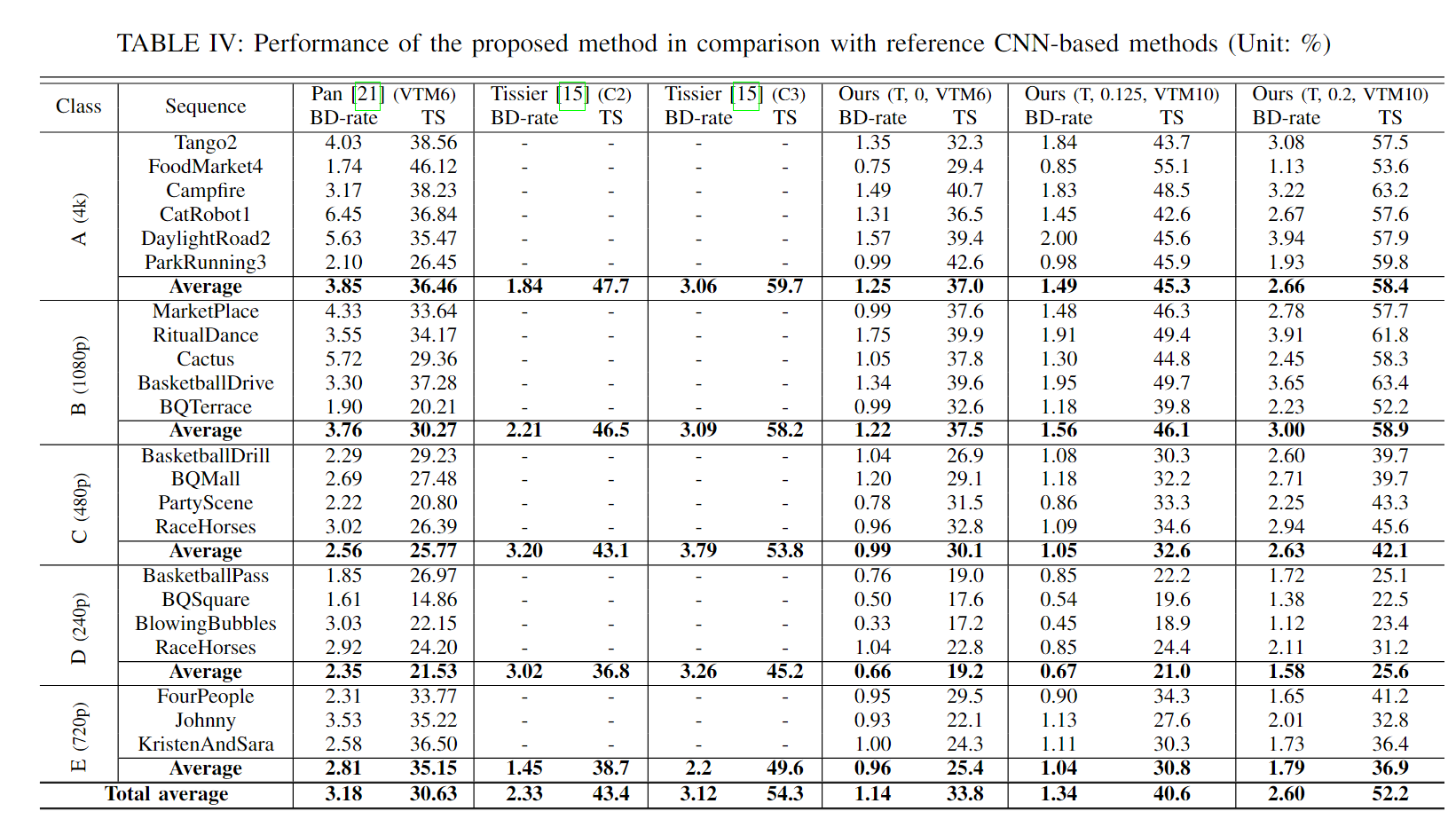
帧间快速算法论文阅读
Low complexity inter coding scheme for Versatile Video Coding (VVC) 通过分析相邻CU的编码区域,预测当前CU的编码区域,以终止不必要的分割模式。 𝐶𝑈1、𝐶𝑈2、𝐶𝑈3、&#x…...

mooc单元测验第一单元
TCP和OSI参考模型对比 OSI参考模型与TCP/IP参考模型(计算机网络)_osi模型 tcpip模型_李桥桉的博客-CSDN博客 会话层和物理层...
AOC显示器出问题了?别担心,简单重置一下就OK了
你的AOC显示器有问题吗?它是被卡在特定的屏幕上还是根本不显示任何图像?如果你的显示器出现任何问题,只需简单重置即可解决问题。 重置AOC显示器可以帮助解决一系列问题,例如颜色或显示设置问题、输入源检测问题以及其他与软件相…...
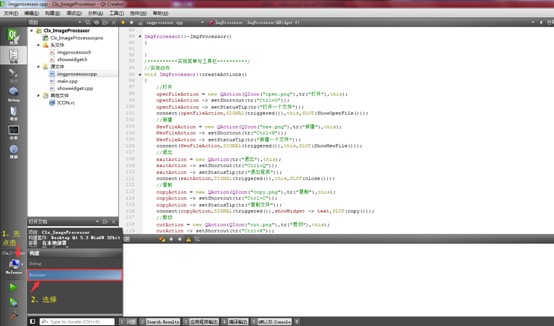
ok-解决qt5发布版本,直接运行exe缺少各种库的问题
已实验第二种方法可用。 工具:电脑必备、QT下的windeployqt Qt 官方开发环境使用的动态链接库方式,在发布生成的exe程序时,需要复制一大堆 dll,如果自己去复制dll,很可能丢三落四,导致exe在别的电脑里无法…...
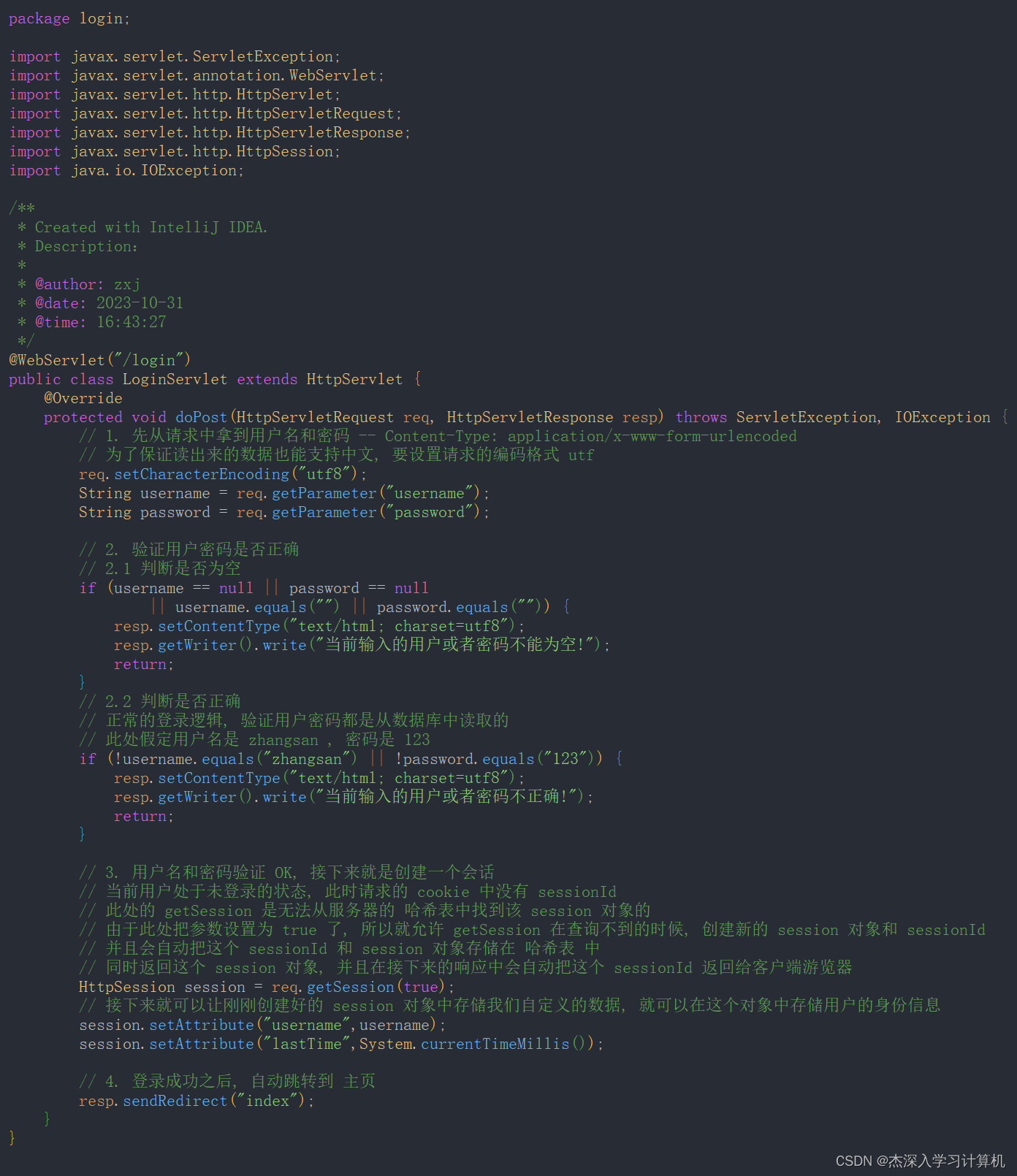
【JavaEE】cookie和session
cookie和session cookie什么是 cookieServlet 中使用 cookie相应的API Servlet 中使用 session 相应的 API代码示例: 实现用户登陆Cookie 和 Session 的区别总结 cookie 什么是 cookie cookie的数据从哪里来? 服务器返回给浏览器的 cookie的数据长什么样? cookie 中是键值对…...

关于CSS的几种字体悬浮的设置方法
关于CSS的几种字体悬浮的设置方法 1. 鼠标放上动态的2. 静态的(位置看上悬浮)2.1 参考QQ邮箱2.2 参考知乎 1. 鼠标放上动态的 效果如下: 代码如下: <!DOCTYPE html> <html lang"en"> <head><met…...
心脏骤停急救赋能
文章目录 0. 背景知识1. 遇到有人突然倒地怎么办1.1 应急反应系统1.2 高质量CPR1.2.1 胸外按压1.2.2 人工呼吸 1.3 AED除颤1.3.1 AED用法 1.4 高级心肺复苏1.5 入院治疗1.6 康复 0. 背景知识 中国每30s就有人倒地,他们可能是工作压力大的年轻人(工程师群…...

Android 13.0 根据app包名授予app监听系统通知权限
1.概述 在13.0的系统rom产品定制化开发中,在一些产品rom定制化开发中,系统内置的第三方app需要开启系统通知权限,然后可以在app中,监听系统所有通知,来做个通知中心的功能,所以需要授权获取系统通知的权限,然后来顺利的监听系统通知。来做系统通知的功能,接下来来实现…...
校园招聘系统
校园管理系统 公共模块学生端游客端企业联系人端校内管理员端超级管理员端企业端 公共模块 登录 用户可以通过验证码、账号密码进行登录。 个人中心 学生端 学生主要为查看招聘信息以及投递等。 首页 简历详情投递 双选会公司详情 公告通知 学生端主要为这些等等…...

SpringBoot-SpringCache缓存
文章目录 Spring Cache 介绍常用注解 Spring Cache 介绍 Spring Cache 是一个框架,实现了基于注解的缓存功能,只需要简单地加一个注解,就能实现缓存功能。 Spring Cache 提供了一层抽象,底层可以切换不同的缓存实现,…...
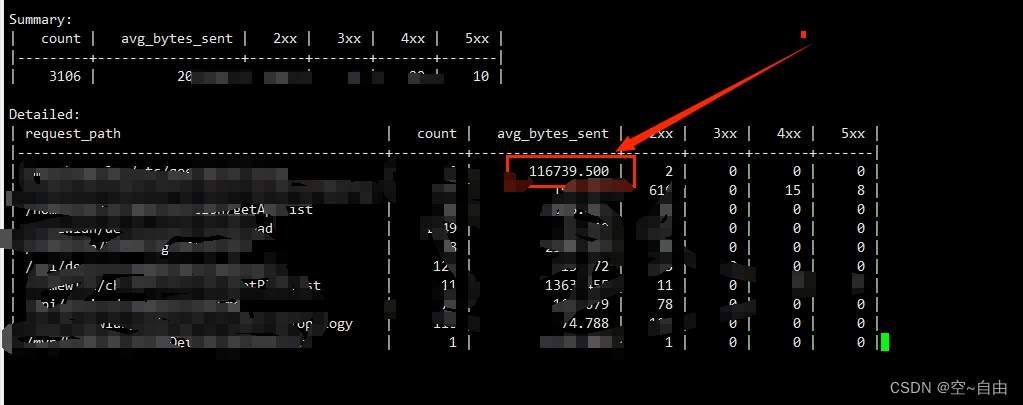
服务器带宽忽然暴增,不停的触发告警
问题: 线上环境,服务器的外网下行带宽达到某个阈值,触发告警,查了下服务器的带宽监控信息,是从某个时间开始突然串上去的,然后监控图形非常有规律,都是每秒达到顶峰后,又立马下去了…...

Linux学习笔记之二(环境变量)
Linux learning note 1、环境变量1.1、修好PATH环境变量 1、环境变量 环境变量(environment variables)即系统运行的一些环境参数。主要的环境变量有以下这些: PATH:决定了系统查找可执行文件的目录范围。HOME:指定当前用户的主目录路径。U…...
)
设计模式——备忘录模式(Memento Pattern)
文章目录 一、备忘录模式定义二、例子2.1 菜鸟例子2.1.1 定义副本类2.1.2 定义对象2.1.3 定义CareTaker 类2.1.3 使用 2.2 JDK —— Date 三、其他设计模式 一、备忘录模式定义 类型: 行为型模式 目的: 保存一个对象的某个状态,以便在适当的…...

C++ 代码实例:多项式除法简单计算工具
文章目录 前言代码仓库代码说明核心片段 结果总结参考资料作者的话 前言 C 代码实例:多项式除法简单计算工具。 代码仓库 yezhening/Programming-examples: 编程实例 (github.com)Programming-examples: 编程实例 (gitee.com) 代码 说明 由于代码篇幅较多&#…...

MySql表自修改报错:You can‘t specify target table ‘student‘ for update in FROM clause
文章目录 一、发现问题二、场景1:在where条件中查询了修改表的数据三、场景2:在set语句中查询了修改表的数据 一、发现问题 在一次准备处理历史数据sql时,出现这么一个问题:You cant specify target table 表名 for update in FR…...
LeetCode 热题100——链表专题
一、俩数相加 2.俩数相加(题目链接) 思路:这题题目首先要看懂,以示例1为例 即 342465807,而产生的新链表为7->0->8. 可以看成简单的从左向右,低位到高位的加法运算,4610,逢…...

植物花粉深度学习图片数据集大合集
最近收集了一波有关于植物花粉的图片数据集,可以用于相关深度学习模型的搭建,废话不多说,上数据集!!! 1、23种花粉类型805张花粉图像数据集 关于此数据:花粉种类和类型的分类是法医抱粉学、考…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
