【电路笔记】-串联RLC电路分析
串联RLC电路分析
文章目录
- 串联RLC电路分析
- 1、概述
- 2、瞬态响应
- 3、AC响应
- 4、RCL和CLR配置
- 5、结论
电阻器 ®、电感器 (L) 和电容器 © 是电子器件中的三个基本无源元件。 它们的属性和行为已在交流电阻、交流电感和交流电容文章中详细介绍。
在本文中,我们将重点讨论这三个组件的串联组合(称为串联 RLC 电路)。 首先,演示部分总结了三个组成组件的交流行为,并简要介绍了 RLC 电路。

在第二部分中,我们讨论该电路在直流电压阶跃下的电气行为,并强调为什么这种特定响应很重要。
接下来,我们在第三部分中通过计算和绘制 RLC 电路的传递函数来重点关注 RLC 电路的交流响应。
最后,我们通过在彼此之间切换组件来提出 RLC 电路的两种替代方案,我们看到交流响应变得完全不同。
1、概述
下面的图 1 给出了 RLC 电路的表示:

该电阻器是纯电阻元件,其两端的电压和电流之间不存在相移。 其阻抗 ( Z R Z_R ZR) 在直流和交流状态下保持相同,等于 R R R(以 Ω \Omega Ω 为单位)。
电感器是纯电抗元件,相移为 +90° 或 + π / 2 +\pi/2 +π/2 rad。 其阻抗由 Z L = j ω L Z_L=j\omega L ZL=jωL 给出,其中 ω \omega ω 是交流情况下电压/电流的角脉动,L 是电感(以 H H H 为单位)。 在直流状态下,电感器表现为两个端子之间的短路,而在交流状态下,当阻抗随频率增加时,电感器会变成开路。
电感器通常被视为抵抗电流变化的组件。
电容器也是纯电抗元件,但其相移为-90°或 − π / 2 -\pi/2 −π/2 rad。 其阻抗由 Z C = − j / C ω Z_C=-j/C\omega ZC=−j/Cω 给出,其中 C C C 为电容(以 F F F 为单位),因此当频率增加时,它在直流状态下表现为开路,在交流状态下表现为短路。
电容器通常被视为抵抗电压变化的组件。
在图 1 中,这三个组件串联互连。 该电路由直流或交流电源供电,输出是电容器两端的电压。 电路的总阻抗是前面所述的独立阻抗的总和:

在下一节中,我们将介绍该电路对电压阶跃的响应,也称为瞬态响应。
2、瞬态响应
在本节中,我们将重点关注图 1 中所示电路在应用 Heaviside 步骤 H ( t ) H(t) H(t) 时的行为:

Heaviside 步骤的特征是, t < 0 t<0 t<0 时等于 0, t > 0 t>0 t>0 时等于 V i n V_{in} Vin。 这两种状态之间的转换类似于脉冲,因为当 t = 0 t=0 t=0 时导数趋向于 + ∞ +\infin +∞。
通过对电路进行网格分析,我们可以写出 V i n = R × I + L × d I / d t + V o u t V_{in}=R×I+L×dI/dt+V_{out} Vin=R×I+L×dI/dt+Vout。 此外,我们知道电流可以改写为 I = C × d V o u t / d t I=C×dV_{out}/dt I=C×dVout/dt,从而得到以下二阶微分方程:

该方程的解是永久响应(时间恒定)和瞬态响应 V o u t V_{out} Vout, t r tr tr(时间变化)之和。 永久响应很容易且明显地找到,解 V o u t = V i n V_{out}=V_{in} Vout=Vin 确实是等式1 的永久解。
瞬态响应的确定很复杂,涉及许多步骤,本文将不详细介绍。 我们承认它的表达式可以采用三种不同的形式,并且取决于称为电路品质因数的 Q = ( 1 / R ) L / C Q=(1/R)\sqrt{L/C} Q=(1/R)L/C 的值。 另一个重要参数是 ω 0 = 1 / L C \omega_0=1/\sqrt{LC} ω0=1/LC,它是电路的基本脉动。
当 Q > 1 / 2 Q>1/2 Q>1/2 时,该状态被称为伪周期或欠阻尼响应,瞬态响应可以写成 V o u t , t r = A e − α t cos ( ω t + ϕ ) V_{out,tr}=Ae^{-\alpha t}\cos(\omega t+\phi) Vout,tr=Ae−αtcos(ωt+ϕ) 的形式。 常数 A A A、 α \alpha α 和 ϕ \phi ϕ 可以通过考虑电路的初始条件(电容器是否充电……)来找到。 脉动 ω \omega ω被称为伪脉动并且取决于基本脉动 ω 0 \omega_0 ω0。
最后, Q = 1 / 2 Q=1/2 Q=1/2 时的最后一种情况,对应于临界状态或临界阻尼响应。 在这种情况下, V o u t , t r = ( A + B t ) e − ω 0 t V_{out,tr}=(A+Bt)e^{-\omega_0t} Vout,tr=(A+Bt)e−ω0t。
需要记住的重要一点是,这些不同的解决方案决定了电压 V o u t V_{out} Vout 如何表现,并在应用 Heaviside 步骤时趋向于其永久值 V i n V_{in} Vin:

我们可以通过开始说随着时间的增加每条曲线都趋于 0 来讨论这个数字。 这是有道理的,因为我们知道 V o u t = V i n + V o u t , t r V_{out}=V_{in}+V_{out,tr} Vout=Vin+Vout,tr 且 V o u t ( t → + ∞ ) = V i n V_{out}(t→+\infin)=V_{in} Vout(t→+∞)=Vin,因此, V o u t , t r → 0 Vout,tr→0 Vout,tr→0。
然而,不同的可能瞬态响应在相同的速度和行为下不会趋于 0。 临界状态是最快趋于 0 的状态,而非周期状态最慢。 伪周期状态呈现振幅呈指数下降的振荡。
对于未知的 RLC 电路,识别瞬态响应并将其与最佳可能曲线相匹配可以为我们提供电路的重要属性,例如 ω 0 \omega_0 ω0 和 Q Q Q。
3、AC响应
在本节中,我们考虑图 1 中所示的相同电路,现在提供交流电源。 利用复数表示中 d X / d t = j ω X dX/dt=j\omega X dX/dt=jωX 的性质,其中 ω \omega ω 是源的角脉动,我们可以将方程 1 重写为以下形式:

然后我们可以表达 V o u t / V i n V_{out}/V_{in} Vout/Vin 的比率,它是串联 RLC 电路的传递函数 T T T:

知道 Q = ( 1 / R ) L / C Q=(1/R)\sqrt{L/C} Q=(1/R)L/C、 ω 0 = 1 / L C \omega_0=1/\sqrt{LC} ω0=1/LC并考虑参数 x = ω / ω 0 x=\omega/\omega_0 x=ω/ω0(称为减少脉动),我们可以重新排列等式3,以写出规范形式 传递函数简化并使得表达式更加紧凑:

绘制传递函数的范数以获得作为参数x的函数的电路增益是很有趣的。 本例中取值 R = 10 Ω R=10\Omega R=10Ω 和 20 Ω 20\Omega 20Ω、 L = 0.2 H L=0.2H L=0.2H 和 C = 100 μ F C=100\mu F C=100μF:

我们可以注意到,图 1 中的串联 RLC 电路在交流状态下充当二阶低通滤波器,因为它会降低高于 ω 0 \omega_0 ω0(通常称为电路的谐振频率)的脉动的输出信号。
二阶滤波器具有稍微放大 ω 0 \omega_0 ω0 附近频率的信号的特性,并在截止频率之后呈现 -40dB/dec 的下降,而不是像一阶滤波器那样仅 -20dB/dec。
图 4 中突出显示了 Q Q Q 值(取决于 R R R)对曲线形状的影响。 谐振频率附近的峰值确实由其带宽 △ ω = ω 0 / Q \triangle \omega =\omega_0/Q △ω=ω0/Q 来表征。
在此示例中, ω 0 = 223 \omega_0=223 ω0=223 rad/s 且 Q = 4.5 Q=4.5 Q=4.5 或 2.25,这为橙色曲线提供了较窄的带宽 △ ω = 50 \triangle \omega=50 △ω=50rad/s,为蓝色曲线提供了 100rad/s 的较宽带宽。 因此,我们可以注意到,品质因数决定了谐振是窄(大 Q Q Q)还是宽(小 Q Q Q)。
如上一节所述,用最佳曲线拟合未知电路的传递函数使我们能够了解电路的属性,从而确定其组成元件的值。
4、RCL和CLR配置
基本元件R、L和C的其他组合可以提供不同类型的滤波器。 我们之前已经看到,RLC 配置是二阶低通滤波器,但是如果我们在它们之间切换一些组件会怎么样?
图 5 和图 6 展示了两种新配置,分别称为 RCL 和 CLR 电路:


尽管这些电路与图 1 所示的原始 RLC 电路之间存在微小变化,但交流响应却有很大不同。
确实可以证明,这两个电路的传递函数由等式 4 和 5 给出:


这些新滤波器的性质通过绘制具有相同值的传递函数范数来揭示: R = 10 Ω R=10\Omega R=10Ω 和 20 Ω 20\Omega 20Ω、 L = 0.2 H L=0.2 H L=0.2H 和 C = 100 μ F C=100\mu F C=100μF。

电路 RCL 是二阶高通滤波器,因为它衰减 ω 0 \omega_0 ω0 以下的频率。 电路 CLR 是一个带通滤波器,因为它仅放大 ω 0 \omega_0 ω0附近的频率。 请注意,与上一节中关于曲线形状作为 Q Q Q 的函数的相同评论仍然适用于这两个滤波器。
5、结论
- 串联 RLC 电路只是三个电子元件的串联组合:电阻器、电感器和电容器。 电阻器的阻抗是实数,电感器和电容器的阻抗是纯虚数,电路的总阻抗是这三个阻抗的总和,因此是一个复数。
- 电路的瞬态响应首先在第二部分中定义和介绍。 它包括研究提供海维赛电压阶跃时电路的行为。 通过研究与电路相关的二阶微分方程的可能解,出现了三种可能的情况:
- 欠阻尼响应,信号缓慢振荡至永久值 V i n V_{in} Vin。
- 信号缓慢增加至永久值的过阻尼响应。
- 临界阻尼响应是信号以最快的速度增加到永久值的情况。
- 第三部分介绍了电路的交流响应。 当提供交流信号时,微分方程可以写成复数形式,以便找到电路的传递函数。 绘制该函数的范数表明串联 RLC 电路的行为类似于二阶低通滤波器。
- 在最后一节中,我们研究了称为 RCL 和 CLR 的替代配置。 本节展示了通过简单地切换组件就可以用同一电路制作二阶高通滤波器或带通滤波器。
相关文章:

【电路笔记】-串联RLC电路分析
串联RLC电路分析 文章目录 串联RLC电路分析1、概述2、瞬态响应3、AC响应4、RCL和CLR配置5、结论 电阻器 、电感器 (L) 和电容器 © 是电子器件中的三个基本无源元件。 它们的属性和行为已在交流电阻、交流电感和交流电容文章中详细介绍。 在本文中,我们将重点讨…...

大数据毕业设计选题推荐-家具公司运营数据分析平台-Hadoop-Spark-Hive
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...

【触想智能】工业显示器上市前的检测项目分享
工业显示器在上市前,需要做一项重要的工作,那就是工业显示器出厂前的产品可靠性检测。 工业显示器选择的测试项目相比商用端更为严格,常见的性能测试项目包括高温老化、防尘防水、电磁静电干扰、防摔防撞等,在工业级应用领域&…...

Vue使用epubjs电子书
npmjs: https://www.npmjs.com/package/epubjs 在线电子书转换器 安装: npm i epubjs 简单封装: src/hooks/ import Epub from "epubjs"; import type { Book, Rendition } from epubjs import type { BookOptions } from epubjs/types…...

python机器学习——决策树
决策树 # 模块导入 from sklearn.tree import ExtraTreeRegressor as ETR, DecisionTreeRegressor as DTRExtraTreeRegressor和DecisionTreeRegressor是scikit-learn库中的两种回归模型,用于拟合和预测连续型目标变量。 决策树是一种基于树结构的机器学习算法&…...
) 和 __attribute__((__section__(“*“ “*“)))的使用)
__attribute__((__used__)) 和 __attribute__((__section__(“*“ “*“)))的使用
见:haproxy代码 C语言注册函数和调用函数,便于模块化开发和编程。 #include <stdio.h>#ifdef __APPLE__ #define HA_SECTION(s) __attribute__((__section__("__DATA, " s))) #define HA_SECTION_START(s) __asm("…...
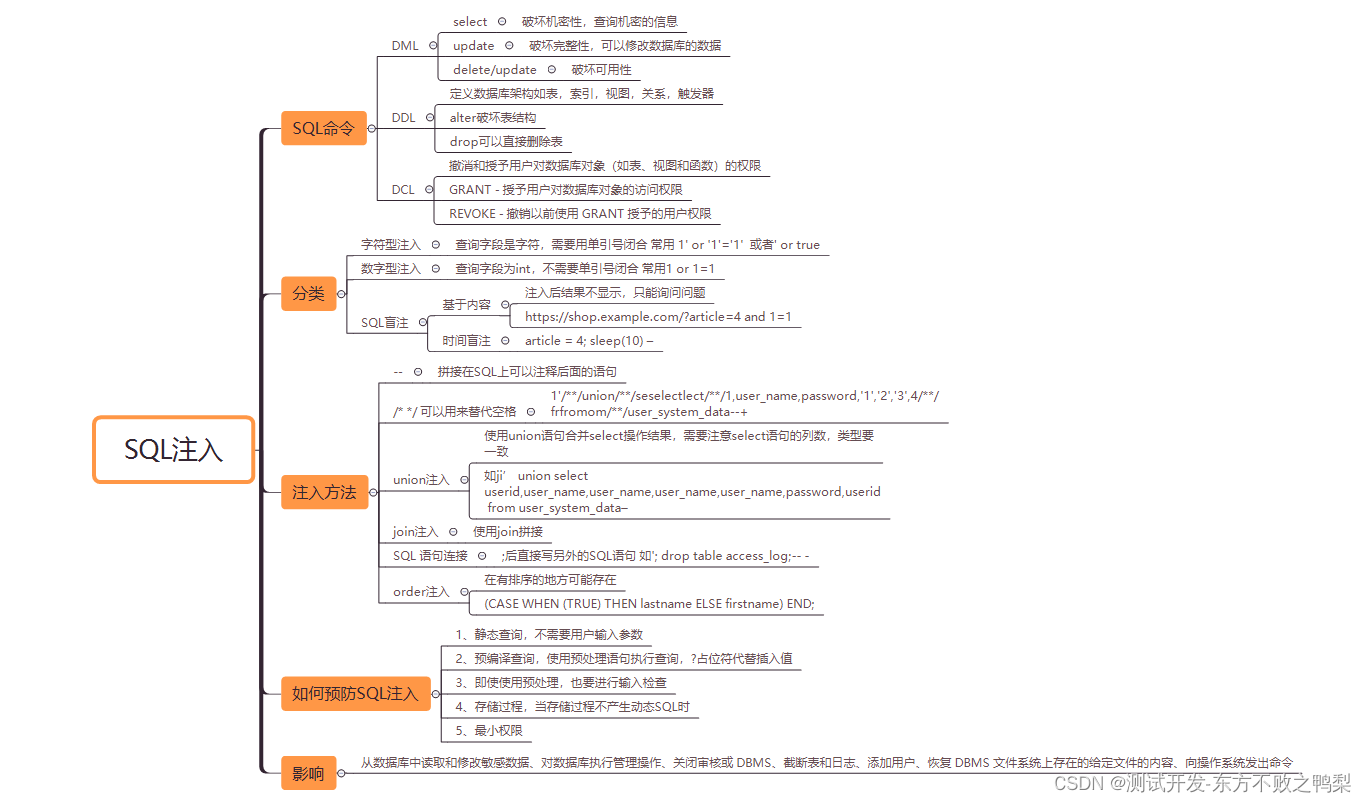
webgoat-(A1)SQL Injection
SQL Injection (intro) SQL 命令主要分为三类: 数据操作语言 (DML)DML 语句可用于请求记录 (SELECT)、添加记录 (INSERT)、删除记录 (DELETE) 和修改现有记录 ÿ…...
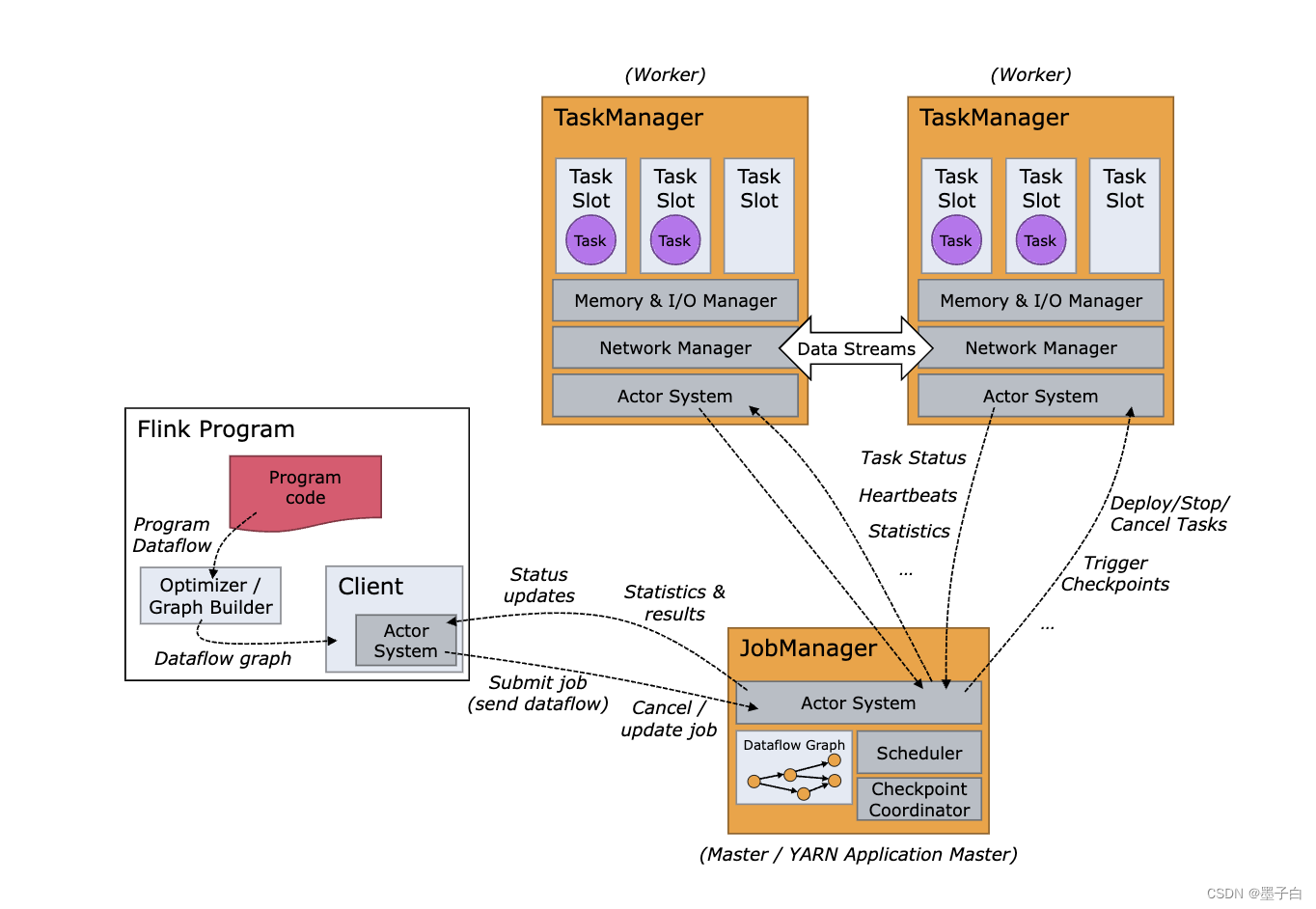
Flink的API分层、架构与组件原理、并行度、任务执行计划
Flink的API分层 Apache Flink的API分为四个层次,每个层次都提供不同的抽象和功能,以满足不同场景下的数据处理需求。下面是这四个层次的具体介绍: CEP API:Flink API 最底层的抽象为有状态实时流处理。其抽象实现是Process Functi…...

Transformer:开源机器学习项目,上千种预训练模型 | 开源日报 No.66
huggingface/transformers Stars: 113.5k License: Apache-2.0 这个项目是一个名为 Transformers 的开源机器学习项目,它提供了数千种预训练模型,用于在文本、视觉和音频等不同领域执行任务。该项目主要功能包括: 文本处理:支持…...
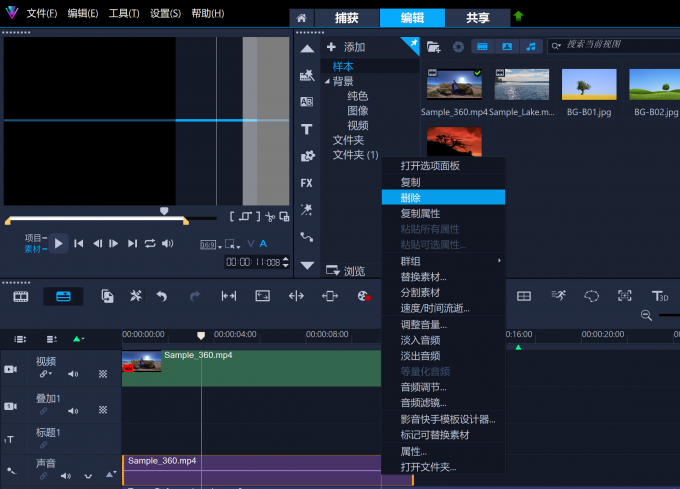
Corel VideoStudio 会声会影2024剪辑中间的视频怎么删 剪辑中音乐太长怎么办
我很喜欢视频剪辑软件Corel VideoStudio 会声会影2024,因为它使用起来很有趣。它很容易使用,但仍然给你很多功能和力量。视频剪辑软件Corel VideoStudio 会声会影2023让我与世界分享我的想法!“这个产品的功能非常多,我几乎没有触…...

数据结构初阶---复杂度的OJ例题
复杂度的OJ例题 一、消失的数字1.思路一2.思路二3.思路三 二、旋转数组1.思路一2.思路二3.思路三 一、消失的数字 数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(N)时间内完成吗? 链接:力扣&…...

Prometheus|云原生|grafana的admin用户密码重置备忘记录
很久很久以前部署的一个Prometheus套装里的grafana密码给忘记了,回忆总是很痛苦,因此还是在这里简单的记录一下,下次就不需要满世界反翻找了。 一, 改库重置密码为admin grafana密码存放在哪里的? 必须说明一下&am…...

[hive]中的字段的数据类型有哪些
Hive中提供了多种数据类型用于定义表的字段。以下是Hive中常见的数据类型: 布尔类型(Boolean):用于表示true或false。 字符串类型(String):用于表示文本字符串。 整数类型(Intege…...
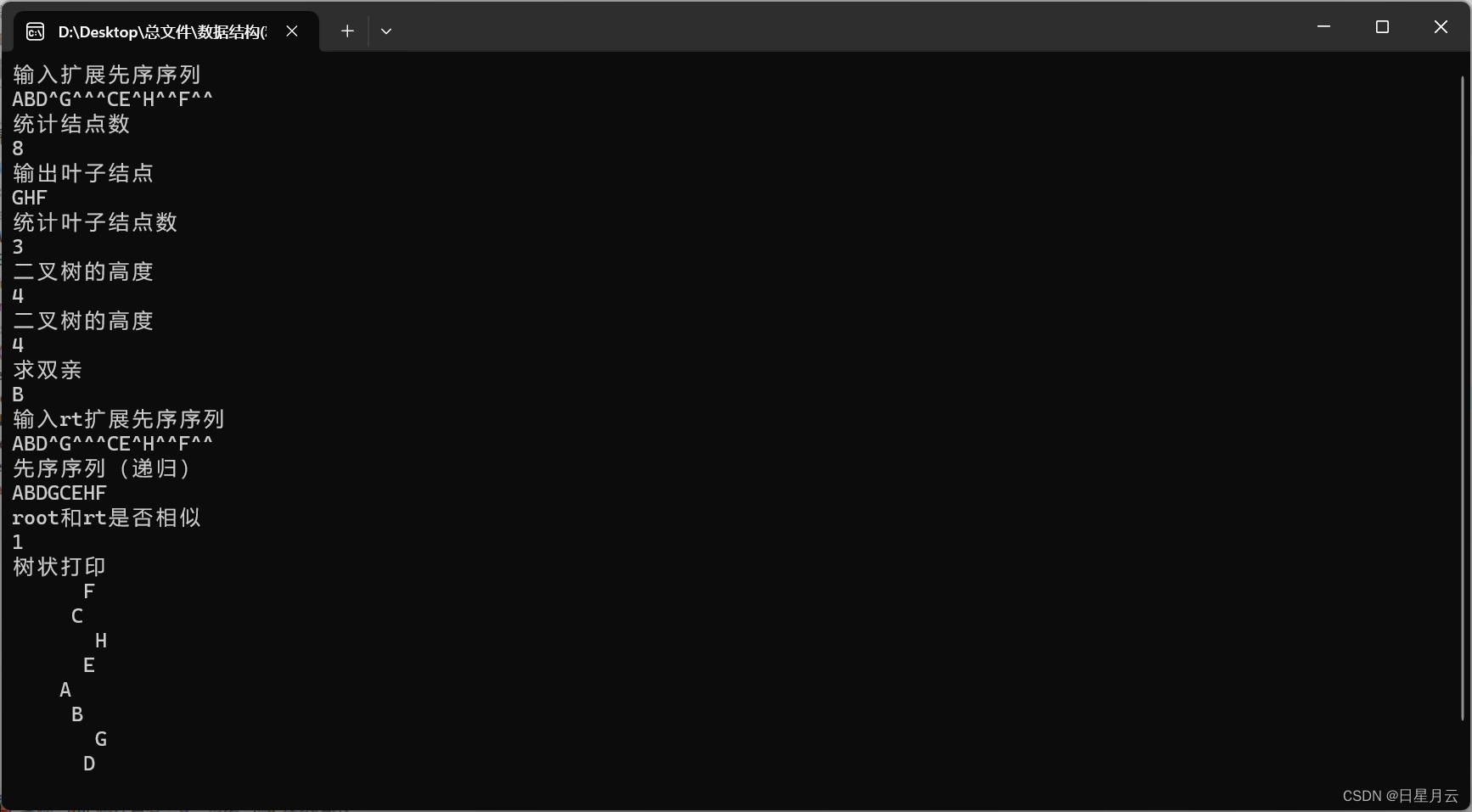
第六章 树【数据结构和算法】【精致版】
第六章 树【数据结构和算法】【精致版】 前言版权第六章 树6.1 应用实例6.2 树的概念6.2.1树的定义与表示6.2.2 树的基本术语6.2.3树的抽象数据类型定义 6.3 二叉树6.3.1二叉树的定义6.3.2 二叉树的性质6.3.3 二叉树的存储 6.4 二叉树的遍历6.4.1 二叉树的遍历及递归实现**1-二…...
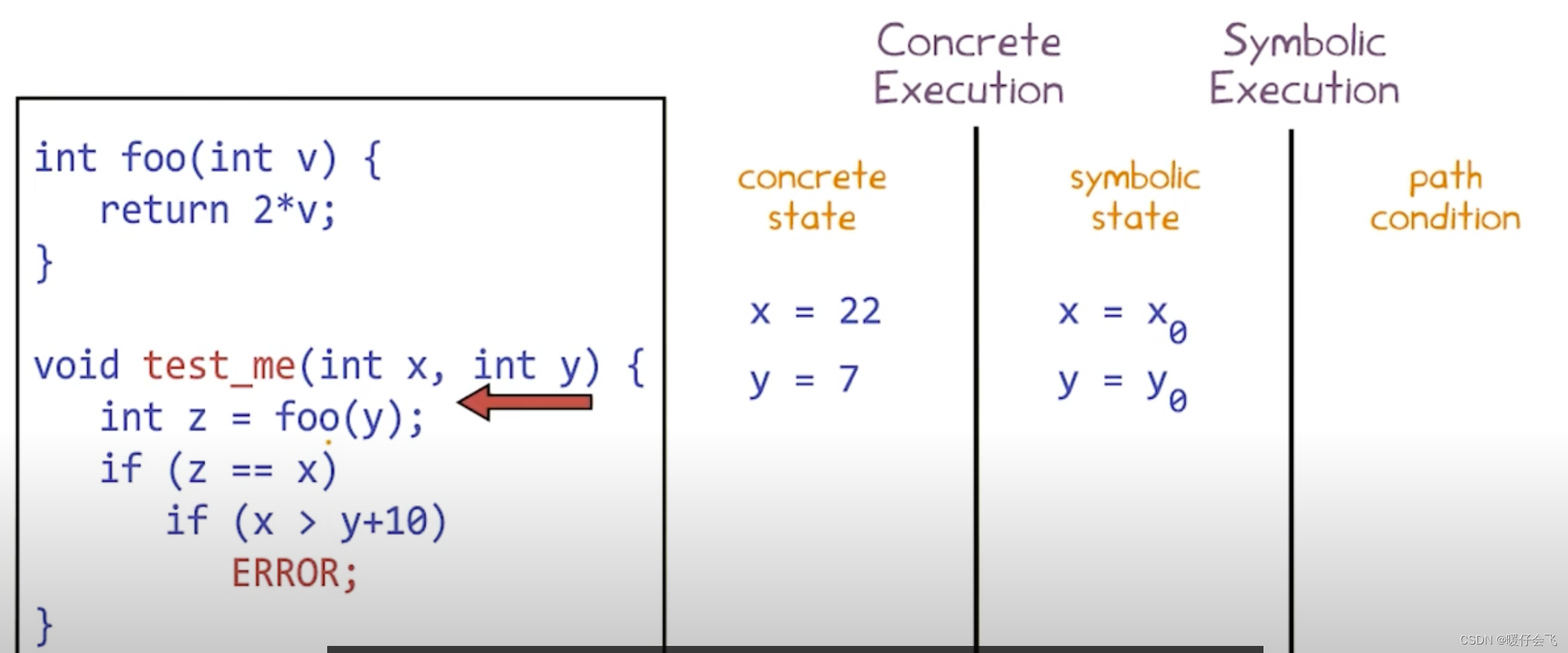
第九章:Dynamic Symbolic Execution
文章目录 Dynamic Symbolic Executionoverviewmotivationdynamic symbolic execution常用的其他技术对比Random Testingsymbolic executionCombined static and symbolic - Dynamic Execution (DSE)step1: 初始化两个具体的值 x,ystep2: 根据定义得出 z 的 concrete value 和 s…...
在搜索引擎中屏蔽csdn
csdn是一个很好的技术博客,里面信息很丰富,我也喜欢在csdn上做技术笔记。 但是CSDN体量太大,文章质量良莠不齐。当在搜索引擎搜索技术问题时,搜索结果中CSDN的内容占比太多,导致难以从其他优秀的博客平台中获取信息。因…...
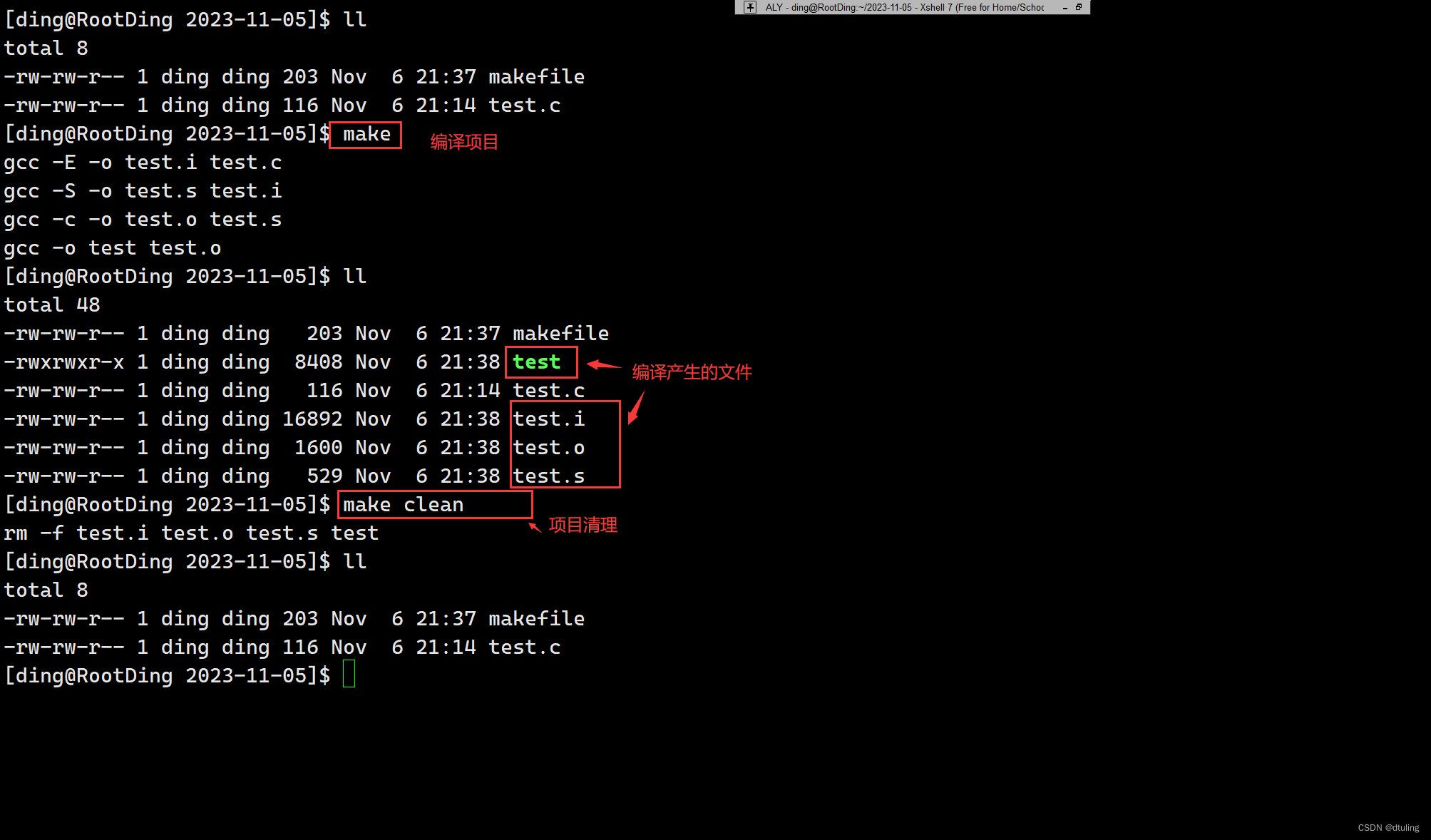
Linux开发工具的使用(vim、gcc/g++ 、make/makefile)
文章目录 一 :vim1:vim基本概念2:vim的常用三种模式3:vim三种模式的相互转换4:vim命令模式下的命令集- 移动光标-删除文字-剪切/删除-复制-替换-撤销和恢复-跳转至指定行 5:vim底行模式下的命令集 二:gcc/g1:gcc/g的作用2:gcc/g的语法3:预处理4:编译5:汇编6:链接7:函…...

MySQL(10):创建和管理表
基础知识 在 MySQL 中,一个完整的数据存储过程总共有 4 步,分别是:创建数据库、确认字段、创建数据表、插入数据。 要先创建一个数据库,而不是直接创建数据表:从系统架构的层次上看,MySQL 数据库系统从大到…...

Python赋值给另一个变量且不改变原变量
Python赋值给另一个变量且不改变原变量 在Python中,如果你想将一个变量的值赋给另一个变量,同时保持原变量不变,你可以使用复制(copy)而不是引用(reference)。Python中的变量通常是通过引用&…...
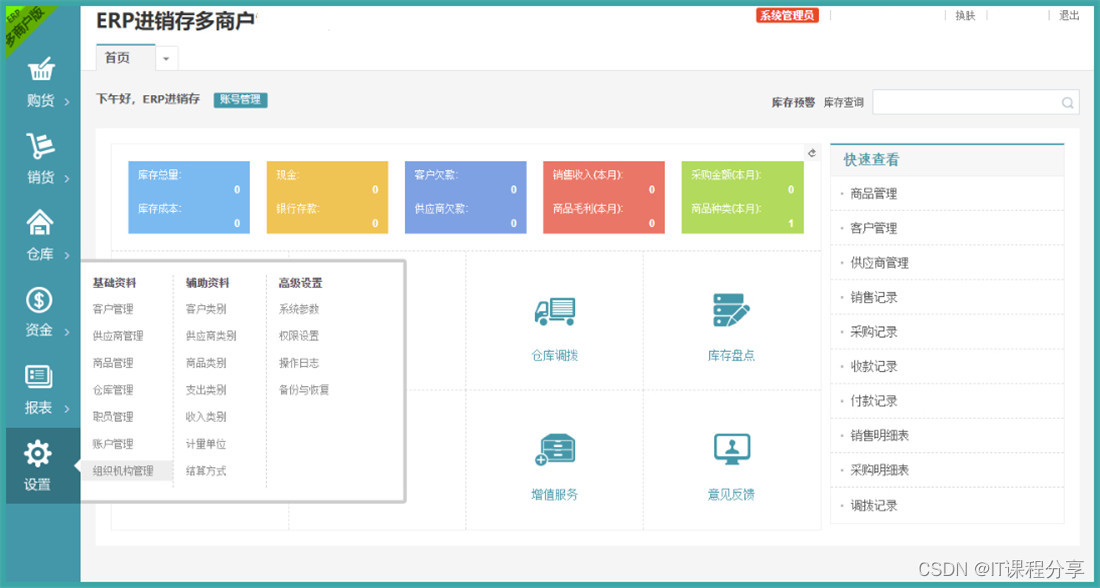
PHP进销存ERP系统源码
PHP进销存ERP系统源码 系统介绍: 扫描入库库存预警仓库管理商品管理供应商管理。 1、电脑端手机端,手机实时共享,手机端一目了然。 2、多商户Saas营销版 无限开商户,用户前端自行注册,后台管理员审核开通 3、管理…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
