力扣370周赛 -- 第三题(树形DP)
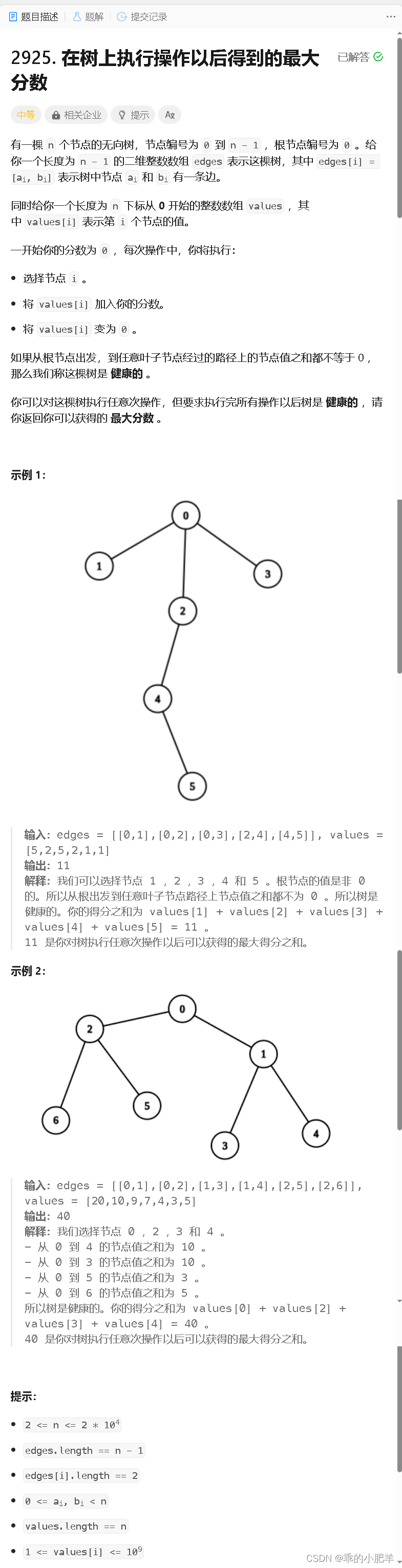
该题的方法,也有点背包的意思,如果一些不懂的朋友,可以从背包的角度去理解该树形DP
问题
题解主要在注释里
//该题是背包问题+树形dp问题的结合版,在树上解决背包问题
//背包问题就是选或不选当前物品
//本题求的是最大分数
//先转成背包问题理解
//从n个物品当中选出最大分数
//再转成有限制版的
//从n个物品当中选出最大分数,并且血量是健康的
//再转成树形DP去理解该问题
//树是健康就是,在任意一条树的路径下(到叶子节点的任意一条路径),能确保至少有一个物品不被选
//从树上前n个物品当中选出一些物品,并且保证树是健康的
//从树上前i个物品当中选出保证树是健康的前提下,能选出的不超过i个物品的最大分数
//然后再去拓展这个定义
//结合树形DP的经验
//以当前u为根节点的子树,在保证树是健康的前提下,能选出的最大分数
//那么就有了推导过程,从下往上推导,也就是从最小子树往上推导到最大子树最大分数
//那么最好的做法就是利用递归的特性,回溯的时候进行推导
//这题中我们直接找出最大分数,其实是比较难的,我们用初中的思想
//正难则反,既然找最大分数(有个不选的)比较难,那么我们可以用
//找个最小分数(选上的),那么就变得比较简单了
//状态定义
//首先我们找最小的,以树形dp为经验推导出
//我们以u为根节点的子树,总和最小的分数(并且是保证健康的,在一条路径上最少也得选一个)
//定义为min_val[u]
//那么怎么算出最大分数呢,既然有min_val[u],那么就有,以当前u为根节点的子树节点总和sum_val[u]
//那么相减sum_val[u] - min_val[u]就等于最大分数了
//那么如何推导这两个定义的数组呢?
//树形dp类型问题,最好首先用dfs,边回溯边推导数组
class Solution {
public:void dfs_sum_val(int u,int fa,vector<int>& val,vector<vector<int>>& g,vector<long long>& sum_val){sum_val[u] = val[u];for(auto e:g[u])if(fa != e)//不要往上计算,我们是从下往上推导{dfs_sum_val(e,u,val,g,sum_val);//回溯计算sum_val[u] += sum_val[e];}//这个dfs我们可以算作一个小题,就是计算出每个点为根节点的子树的总和}void dfs_min_val(int u,int fa,vector<int>& val,vector<vector<int>>& g,vector<long long>& min_val){long long min_res = 0;min_val[u] = (long long)val[u];for(auto& e:g[u]){if(fa != e){dfs_min_val(e,u,val,g,min_val);min_res += min_val[e];}}if(min_res) min_val[u] = min((long long)min_val[u],min_res);}long long maximumScoreAfterOperations(vector<vector<int>>& edges, vector<int>& values) {//该题是背包问题+树形dp问题的结合版,在树上解决背包问题//背包问题就是选或不选当前物品//本题求的是最大分数//先转成背包问题理解//从n个物品当中选出最大分数//再转成有限制版的//从n个物品当中选出最大分数,并且血量是健康的//再转成树形DP去理解该问题//树是健康就是,在任意一条树的路径下(到叶子节点的任意一条路径),能确保至少有一个物品不被选//从树上前n个物品当中选出一些物品,并且保证树是健康的//从树上前i个物品当中选出保证树是健康的前提下,能选出的不超过i个物品的最大分数//然后再去拓展这个定义//结合树形DP的经验//以当前u为根节点的子树,在保证树是健康的前提下,能选出的最大分数//那么就有了推导过程,从下往上推导,也就是从最小子树往上推导到最大子树最大分数//那么最好的做法就是利用递归的特性,回溯的时候进行推导//这题中我们直接找出最大分数,其实是比较难的,我们用初中的思想//正难则反,既然找最大分数(有个不选的)比较难,那么我们可以用//找个最小分数(选上的),那么就变得比较简单了//状态定义//首先我们找最小的,以树形dp为经验推导出//我们以u为根节点的子树,总和最小的分数(并且是保证健康的,在一条路径上最少也得选一个)//定义为min_val[u]//那么怎么算出最大分数呢,既然有min_val[u],那么就有,以当前u为根节点的子树节点总和sum_val[u]//那么相减sum_val[u] - min_val[u]就等于最大分数了//那么如何推导这两个定义的数组呢?//树形dp类型问题,最好首先用dfs,边回溯边推导数组int edge_size = edges.size();vector<vector<int>> g(values.size() + 110);for(int i = 0;i < edge_size;i++){int a = edges[i][0];int b = edges[i][1];g[a].push_back(b);g[b].push_back(a);}vector<long long> sum_val(21000);vector<long long> min_val(21000,0x3f3f3f3f);//预处理出来sum_val数组dfs_sum_val(0,-1,values,g,sum_val);//预处理出来min_val数组dfs_min_val(0,-1,values,g,min_val);return sum_val[0] - min_val[0];}
};相关文章:

力扣370周赛 -- 第三题(树形DP)
该题的方法,也有点背包的意思,如果一些不懂的朋友,可以从背包的角度去理解该树形DP 问题 题解主要在注释里 //该题是背包问题树形dp问题的结合版,在树上解决背包问题 //背包问题就是选或不选当前物品 //本题求的是最大分数 //先转…...

GPT学习笔记
百度的文心一言 阿里的通义千问 通过GPT能力,提升用户体验和产品力 GPT的出现是AI的iPhone时刻。2007年1月9日,第一代iPhone发布,开启移动互联网时代。新一轮的产业革命。 GPT模型发展时间线: Copilot - 副驾驶 应用…...
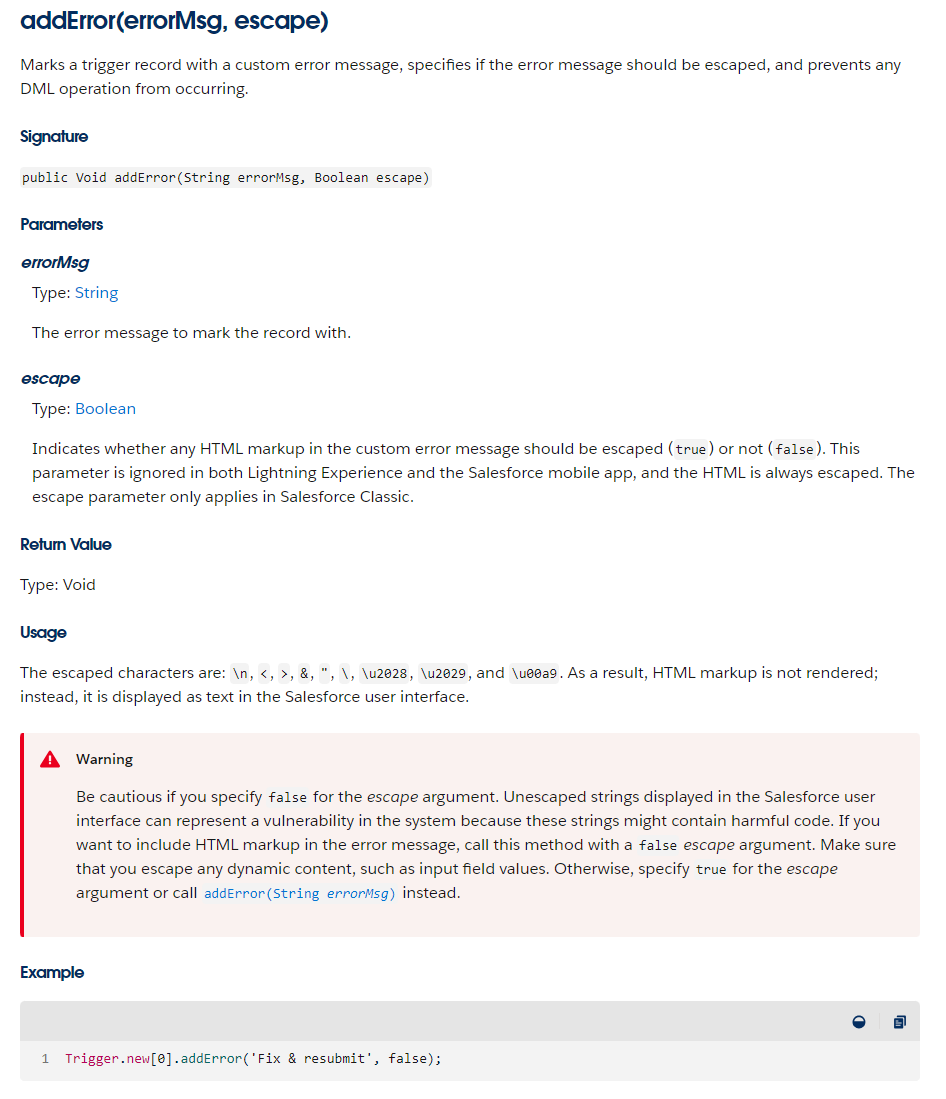
Apex的addError()显示的消息中实现换行
直接用‘<br/>’是无效的,因为addError默认不转义HTML符号,如果需要转义,应该将第二个参数escape设置为false。不过即使设置了也只对classic页面生效,lightning页面还是无法转义。 官方文档: 参考资料…...

STM32中微秒延时的实现方式
STM32中微秒延时的实现方式 0.前言一、裸机实现方式二、FreeRTOS实现方式三、定时器实现(通用)4、总结 0.前言 最近在STM32驱动移植过程中需要用到微秒延时来实现一些外设的时序,由于网上找到的驱动方法良莠不齐,笔者在实现时序过…...
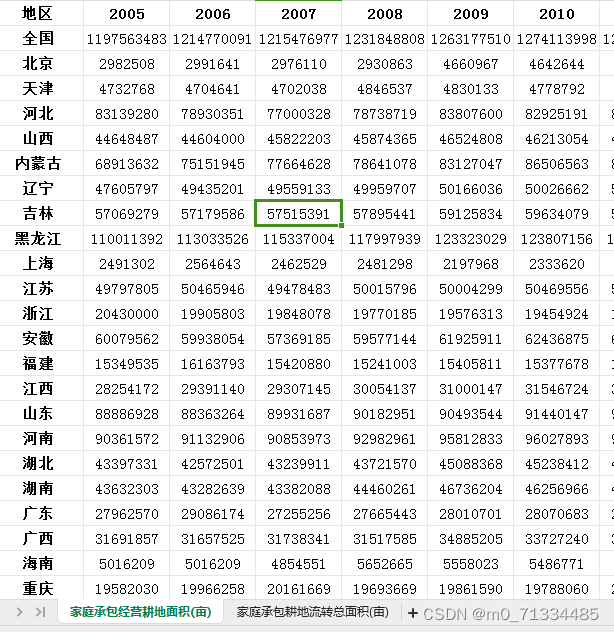
2005-2021年全国各省家庭承包耕地面积和家庭承包耕地流转总面积数据(无缺失)
2005-2021年全国各省家庭承包耕地面积和家庭承包耕地流转总面积数据 1、时间:2005-2021年 2、来源:农村经营管理统计NB 3、指标:家庭承包经营耕地面积、家庭承包耕地流转总面积(单位:亩) 4、范围&#…...
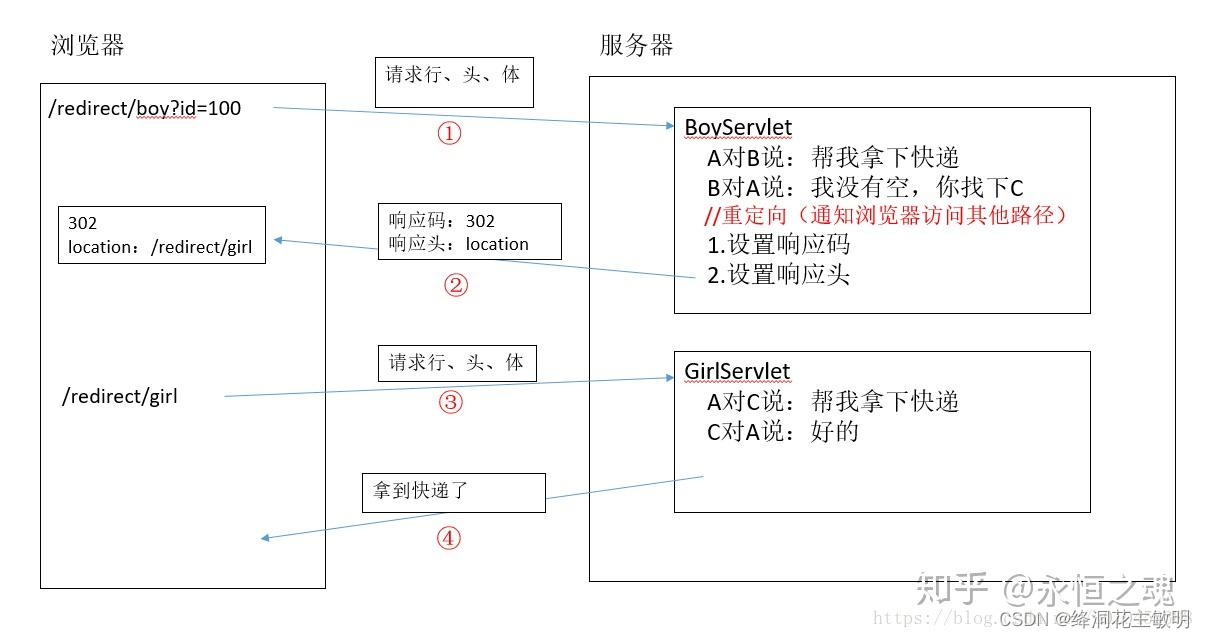
【六、http】go的http的客户端重定向
一、http的重定向 重定向过程:客户浏览器发送http请求----》web服务器接受后发送302状态码响应及对应新的location给客户浏览器–》客户浏览器发现是302响应,则自动再发送一个新的http请求,请求url是新的location地址----》服务器根据此请求寻…...

AI:61-基于深度学习的草莓病害识别
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌在这个漫长的过程,中途遇到了不少问题,但是…...
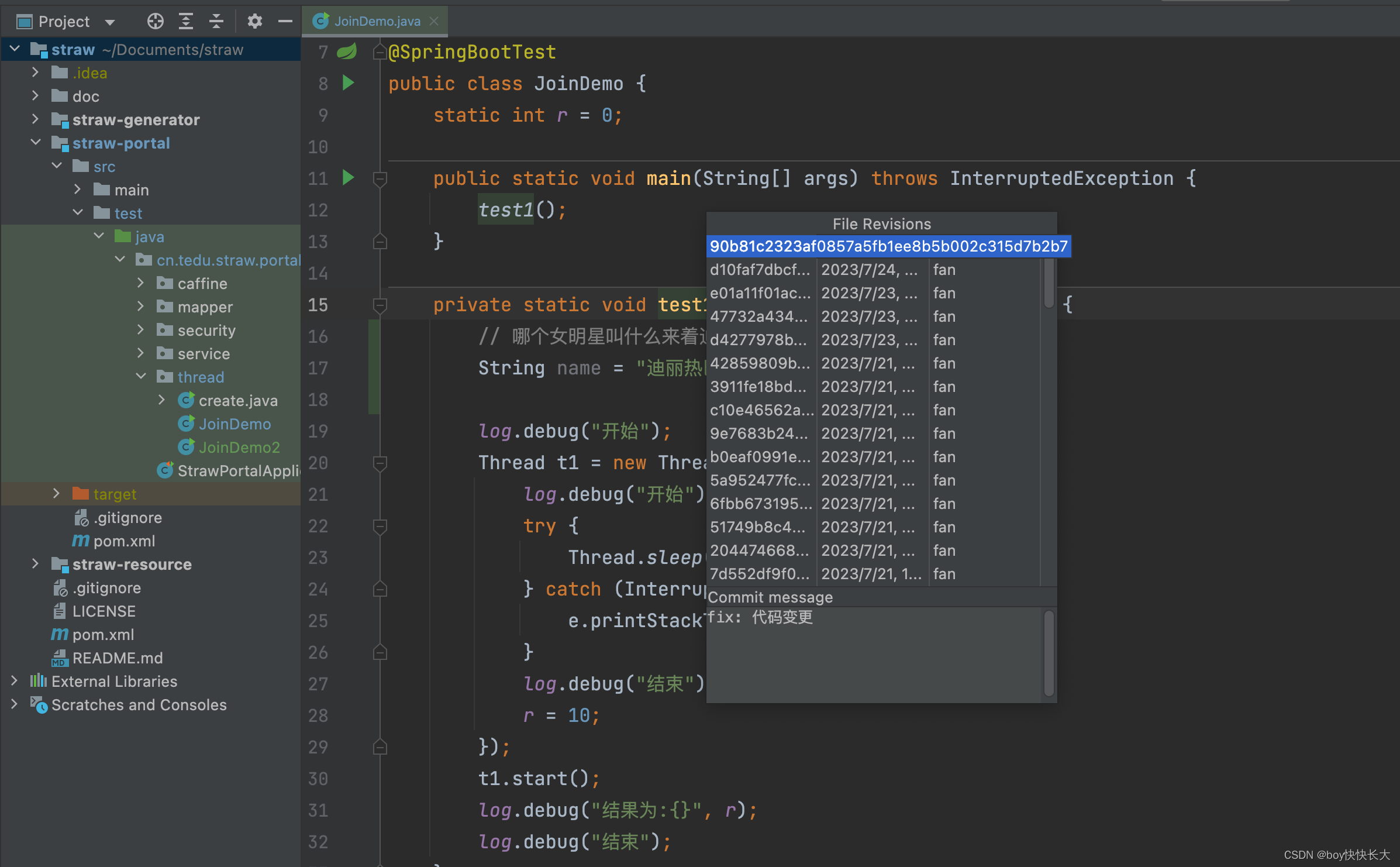
idea文件比对
idea文件比对 1.项目内的文件比对2.项目间的文件比对3. 剪切板对比4. 版本历史(不同分支和不同commit)对比 1.项目内的文件比对 在项目中选择好需要比对的文件(类),然后选择Compare Files Mac下的快捷键是Commandd, 这样的比对像是git冲突解决一样 …...
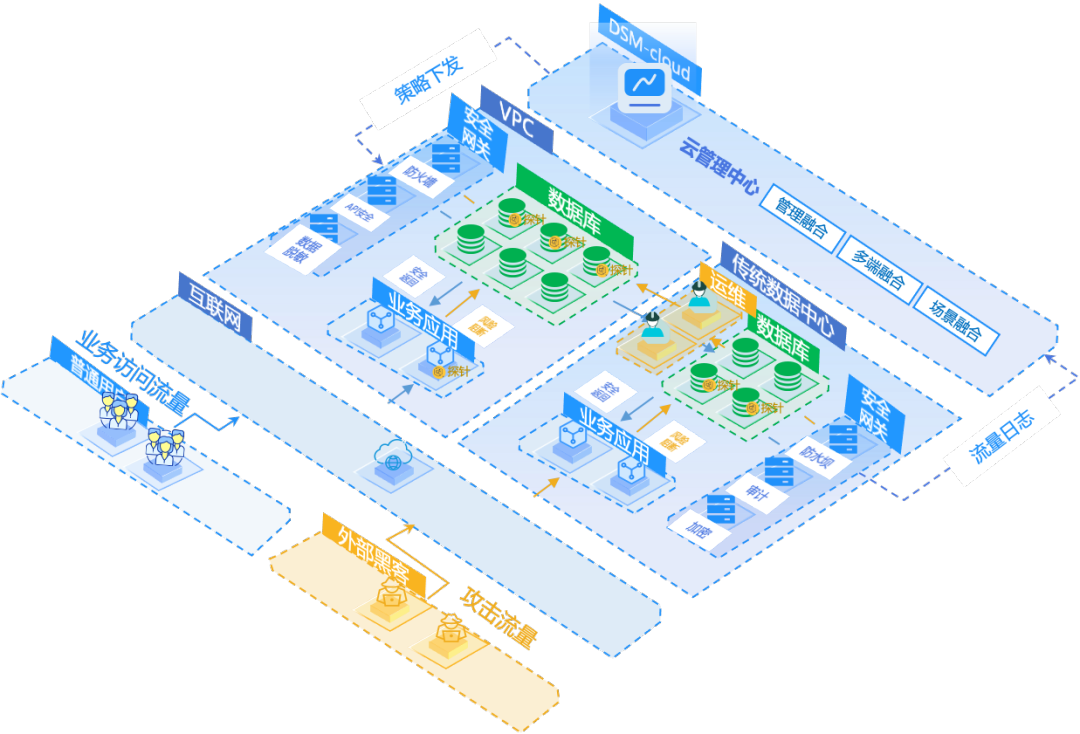
重磅发布|美创科技新一代 数据安全管理平台(DSM Cloud)全新升级
重磅发布 新一代 数据安全管理平台(DSM Cloud) 美创科技新一代 数据安全管理平台(简称:DSM Cloud)全新升级,正式发布。 在业务上云飞速发展过程中,快速应对数据激增,同时有效保障数…...
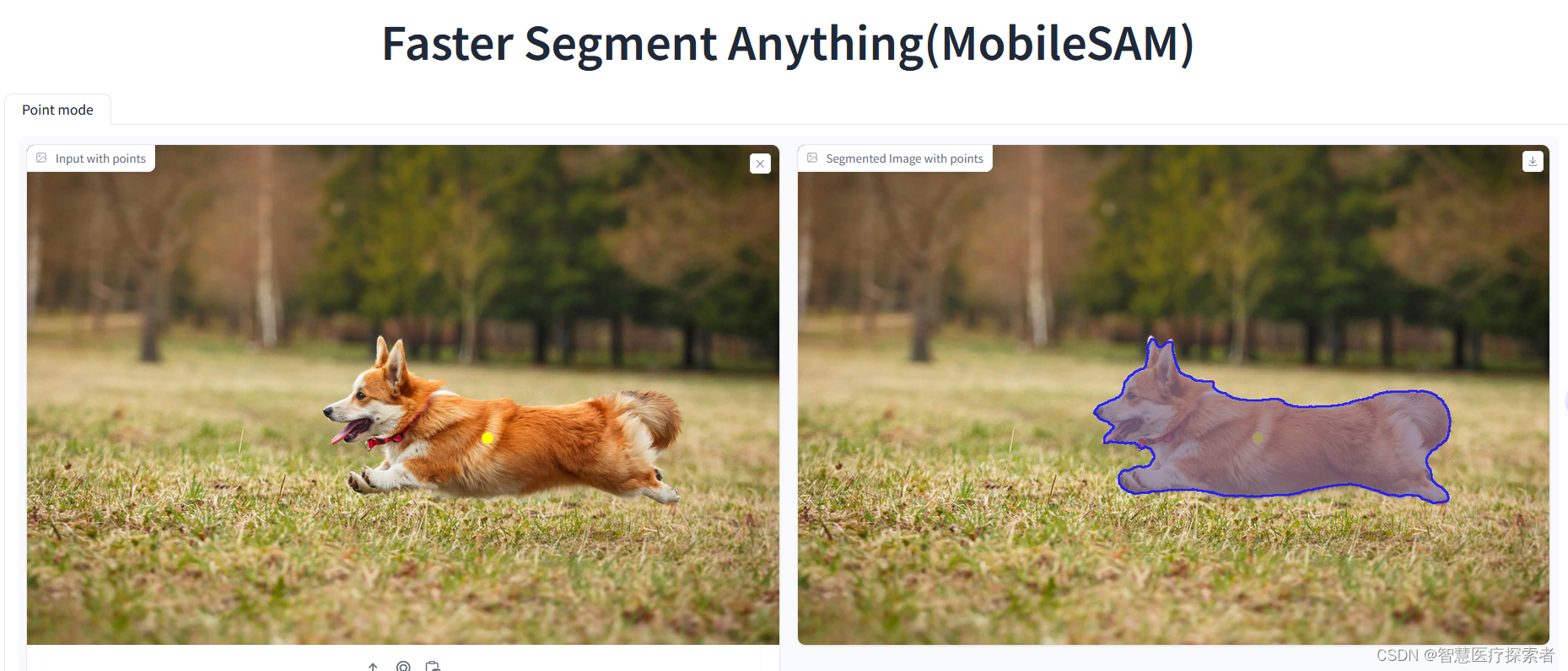
比SAM小60倍的分割一切模型:MobileSAM
1 MobileSAM SAM就是一类处理图像分割任务的通用模型。与以往只能处理某种特定类型图片的图像分割模型不同,SAM可以处理所有类型的图像。 在SAM出现前,基本上所有的图像分割模型都是专有模型。比如,在医学领域,有专门分割核磁图…...
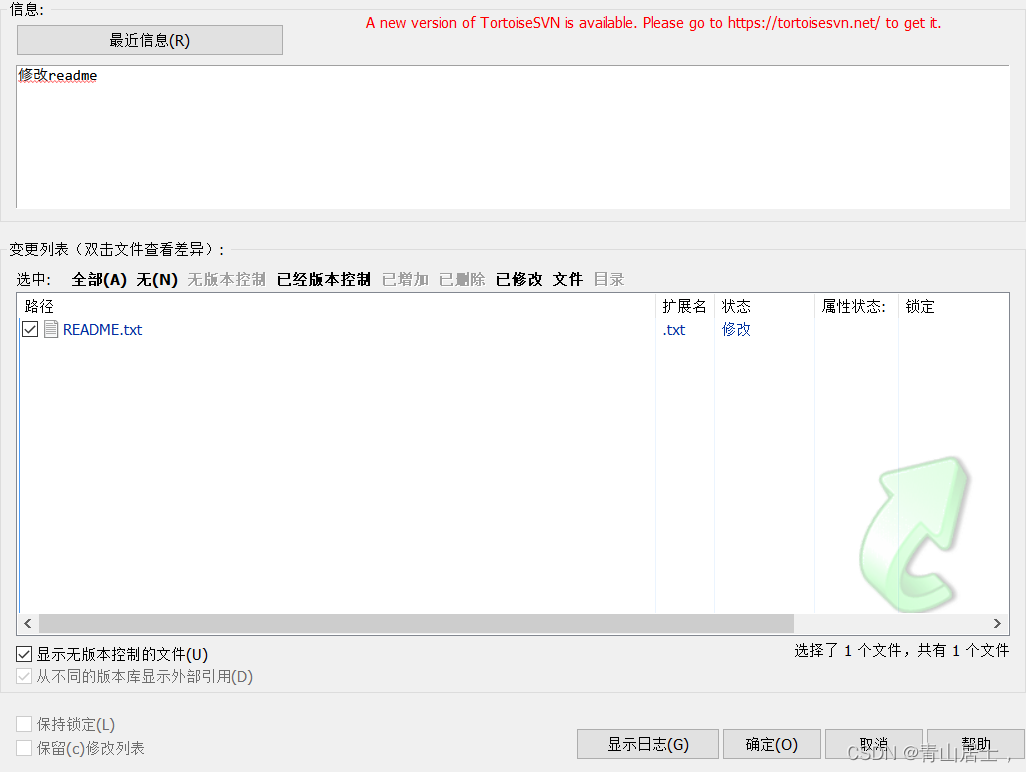
版本控制系统-SVN
SVN Apache Subversion 通常被缩写成 SVN,是一个开放源代码的版本控制系统。 官网:https://subversion.apache.org 资料:https://svnbook.red-bean.com、https://www.runoob.com/svn/svn-tutorial.html 下载:https://sourceforg…...

【电路笔记】-串联RLC电路分析
串联RLC电路分析 文章目录 串联RLC电路分析1、概述2、瞬态响应3、AC响应4、RCL和CLR配置5、结论 电阻器 、电感器 (L) 和电容器 © 是电子器件中的三个基本无源元件。 它们的属性和行为已在交流电阻、交流电感和交流电容文章中详细介绍。 在本文中,我们将重点讨…...

大数据毕业设计选题推荐-家具公司运营数据分析平台-Hadoop-Spark-Hive
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...

【触想智能】工业显示器上市前的检测项目分享
工业显示器在上市前,需要做一项重要的工作,那就是工业显示器出厂前的产品可靠性检测。 工业显示器选择的测试项目相比商用端更为严格,常见的性能测试项目包括高温老化、防尘防水、电磁静电干扰、防摔防撞等,在工业级应用领域&…...

Vue使用epubjs电子书
npmjs: https://www.npmjs.com/package/epubjs 在线电子书转换器 安装: npm i epubjs 简单封装: src/hooks/ import Epub from "epubjs"; import type { Book, Rendition } from epubjs import type { BookOptions } from epubjs/types…...

python机器学习——决策树
决策树 # 模块导入 from sklearn.tree import ExtraTreeRegressor as ETR, DecisionTreeRegressor as DTRExtraTreeRegressor和DecisionTreeRegressor是scikit-learn库中的两种回归模型,用于拟合和预测连续型目标变量。 决策树是一种基于树结构的机器学习算法&…...
) 和 __attribute__((__section__(“*“ “*“)))的使用)
__attribute__((__used__)) 和 __attribute__((__section__(“*“ “*“)))的使用
见:haproxy代码 C语言注册函数和调用函数,便于模块化开发和编程。 #include <stdio.h>#ifdef __APPLE__ #define HA_SECTION(s) __attribute__((__section__("__DATA, " s))) #define HA_SECTION_START(s) __asm("…...
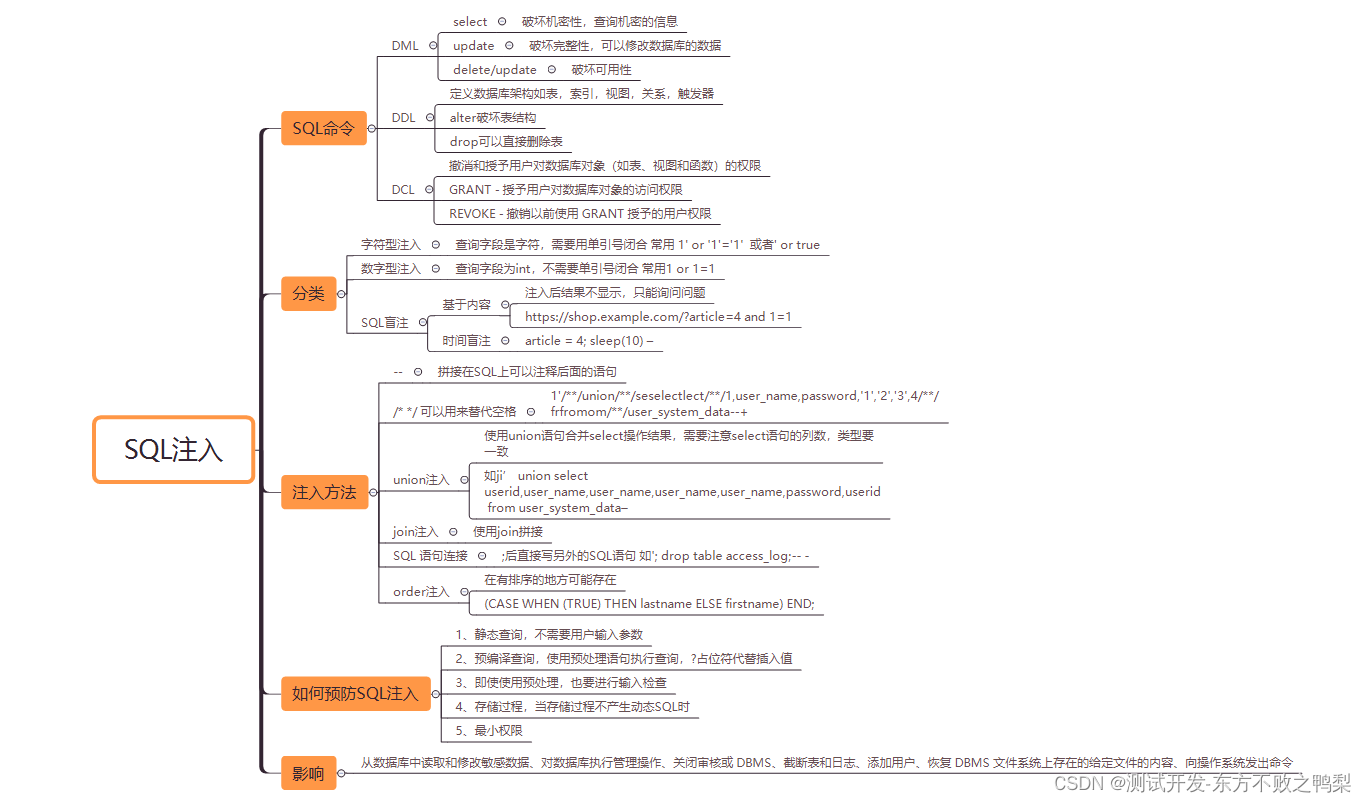
webgoat-(A1)SQL Injection
SQL Injection (intro) SQL 命令主要分为三类: 数据操作语言 (DML)DML 语句可用于请求记录 (SELECT)、添加记录 (INSERT)、删除记录 (DELETE) 和修改现有记录 ÿ…...
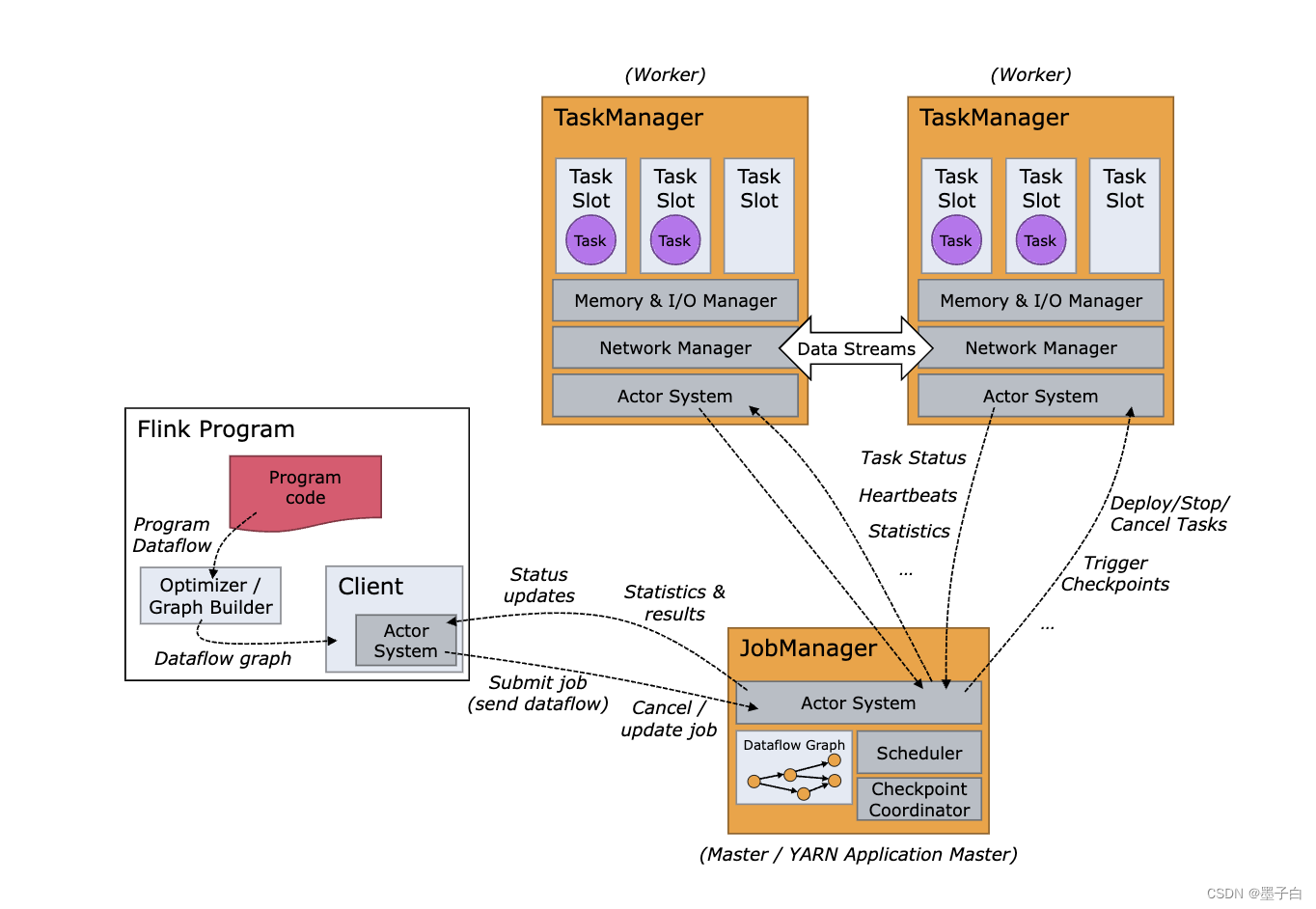
Flink的API分层、架构与组件原理、并行度、任务执行计划
Flink的API分层 Apache Flink的API分为四个层次,每个层次都提供不同的抽象和功能,以满足不同场景下的数据处理需求。下面是这四个层次的具体介绍: CEP API:Flink API 最底层的抽象为有状态实时流处理。其抽象实现是Process Functi…...

Transformer:开源机器学习项目,上千种预训练模型 | 开源日报 No.66
huggingface/transformers Stars: 113.5k License: Apache-2.0 这个项目是一个名为 Transformers 的开源机器学习项目,它提供了数千种预训练模型,用于在文本、视觉和音频等不同领域执行任务。该项目主要功能包括: 文本处理:支持…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
