吴恩达《机器学习》4-6->4-7:正规方程
一、正规方程基本思想
-
正规方程是一种通过数学推导来求解线性回归参数的方法,它通过最小化代价函数来找到最优参数。
-
代价函数 J(θ) 用于度量模型预测值与实际值之间的误差,通常采用均方误差。
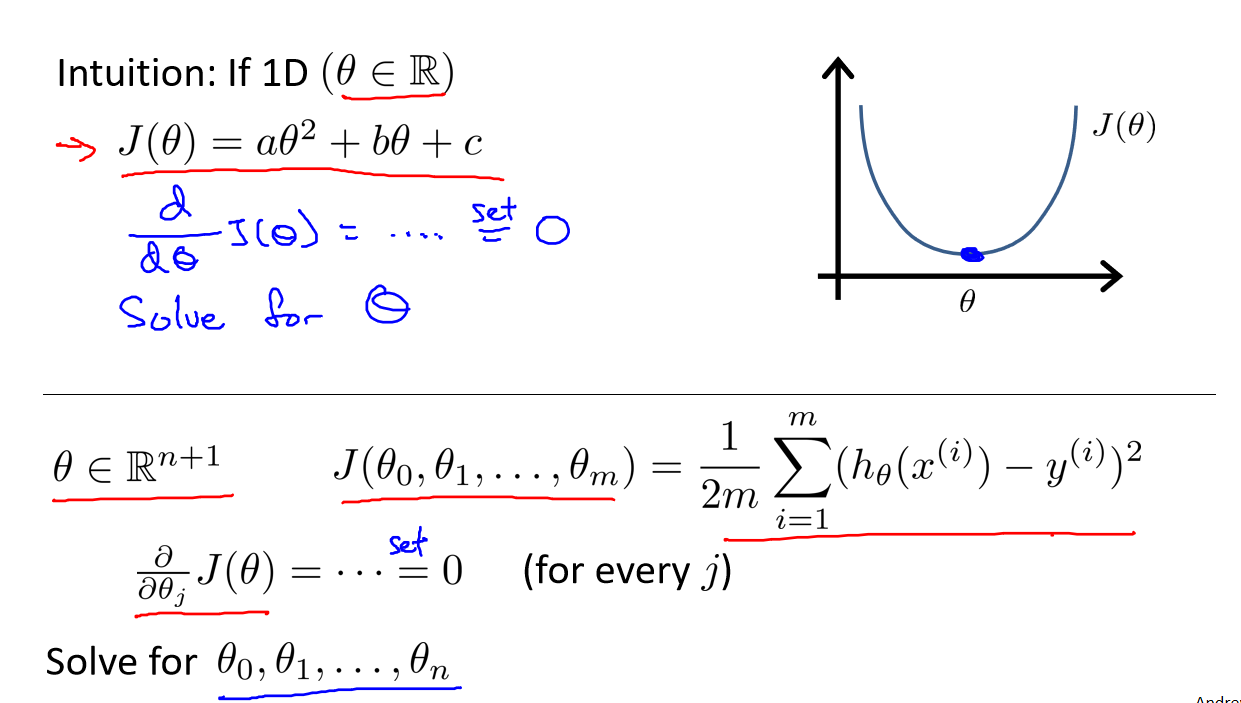
二、步骤
-
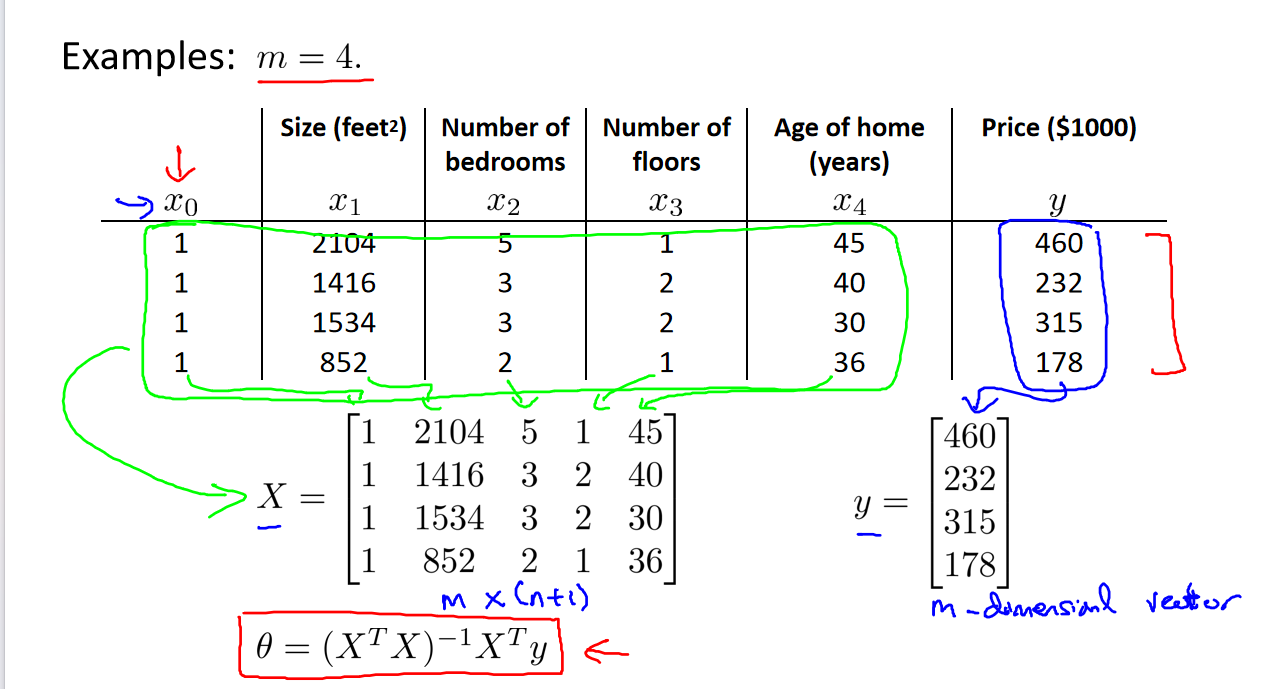
准备数据集,包括特征矩阵 X 和目标向量 y。特征矩阵通常包括一个全为1的常数列(截距项)。
-
定义代价函数 J(θ),通常采用均方误差。
-
推导代价函数 J(θ) 对参数θ的梯度,令梯度为零。
-
将梯度为零的方程组转化为矩阵形式:X^T * X * θ = X^T * y。
-
求解正规方程,得到最优参数θ:θ = (X^T * X)^(-1) * X^T * y。
三、正规方程的优点
-
不需要选择学习率α,一次运算得出最优参数,无需迭代。
-
在特征数量较小的情况下非常适用(通常 n < 10000)。
四、正规方程的限制和适用情况
-
不适用于非线性模型,仅适用于线性回归。
-
如果特征之间存在线性相关性,或者特征数量多于样本数量,正规方程可能不适用。
-
对于特征数量大的情况,计算 (X^T * X)^(-1) 的逆矩阵可能会昂贵。

五、选择算法
-
根据问题的特点、数据集的大小和特征的独立性来选择使用梯度下降法或正规方程。
-
对于小型数据集和特征数量不多的情况,正规方程是一个有效的选择。
六、正规方程在矩阵不可逆时的解决办法
-
使用伪逆函数
pinv():-
在Octave等数值计算工具中,可以使用伪逆函数
pinv()来计算参数θ,即使特征矩阵X^T * X是不可逆的。这是一种弥补不可逆性的方法,它可以提供正确的解。
-
-
处理线性相关的特征:
-
当存在线性相关的特征时,如 x1 = (3.28)^2 * x2,矩阵X^T * X可能变得奇异或不可逆。此时,可以考虑去除一个或多个相关特征以减少特征数量,同时保持数据的信息内容。这将使X^T * X更容易求逆。
-
-
特征选择和正则化:
-
如果特征数量n太多,而训练样本数量m相对较少,可能会导致X^T * X不可逆。在这种情况下,可以考虑以下方法:
-
删除一些不相关或冗余的特征,以降低特征数量。
-
使用正则化方法,如Lasso或Ridge回归,来惩罚不必要的特征权重,从而解决不可逆性问题。
-
-

参考资料:
[中英字幕]吴恩达机器学习系列课程
黄海广博士 - 吴恩达机器学习个人笔记
相关文章:

吴恩达《机器学习》4-6->4-7:正规方程
一、正规方程基本思想 正规方程是一种通过数学推导来求解线性回归参数的方法,它通过最小化代价函数来找到最优参数。 代价函数 J(θ) 用于度量模型预测值与实际值之间的误差,通常采用均方误差。 二、步骤 准备数据集,包括特征矩阵 X 和目标…...

VO、DTO
DTO DTO(Data Transfer Object) 数据传输对象【前后端交互】 也就是后端开发过程中,用来接收前端传过来的参数,一般会创建一个Java对应的DTO类(UserDTO等等) 因为前端一般传来的是Json格式的数据…...

RK3566上运行yolov5模型进行图像识别
一、简介 本文记录了依靠RK官网的文档,一步步搭建环境到最终在rk3566上把yolov5 模型跑起来。最终实现的效果如下: 在rk3566 板端运行如下app: ./rknn_yolov5_demo model/RK356X/yolov5s-640-640.rknn model/bus.jpg其中yolov5s-640-640.r…...

汽车标定技术(一):XCP概述
目录 1.汽车标定概述 2.XCP协议由来及版本介绍 3.XCP技术通览 3.1 XCP上下机通信模型 3.2 XCP指令集 3.2.1 XCP帧结构定义 3.2.2 标准指令集 3.2.3 标定指令集 3.2.4 页切换指令集 3.2.5 数据采集指令集 3.2.6 刷写指令集 3.3 ECU描述文件(A2L)概述 3.3.1 标定上位…...

短视频的运营方法
尊敬的用户们,你们好!今天我将为大家带来一篇关于短视频运营的专业文章。在当今互联网时代,短视频已经成为了一个重要的流量入口,掌握正确的运营方法对于企业的发展至关重要。接下来,我将通过以下几个方面为大家详细介…...
GitLab CI/CD 持续集成/部署 SpringBoot 项目
一、GitLab CI/CD 介绍 GitLab CI/CD(Continuous Integration/Continuous Deployment)是 GitLab 提供的一种持续集成和持续部署的解决方案。它可以自动化软件的构建、测试和部署过程,以便开发者更快地、更频繁地发布可靠的产品。 整体过程如…...

第二证券:政策效应逐步显现 A股修复行情有望持续演绎
上星期,A股商场延续企稳反弹的态势,上证指数震荡上涨0.43%;沪深两市日均成交额回升至8700亿元左右;北向资金近一个月初次转为周净买入5.57亿元。 安排观点一起认为,在稳增加、稳预期相关政策持续发力,上市…...

sql逻辑优化
1.分页 通常使用每页条数及第一页作为参数 开发接口 GetMapping("/querySystemList") public List<SystemAduit> querySystemList(RequestParam("keyword") String keyword,RequestParam(name "offset", defaultValue "0") i…...
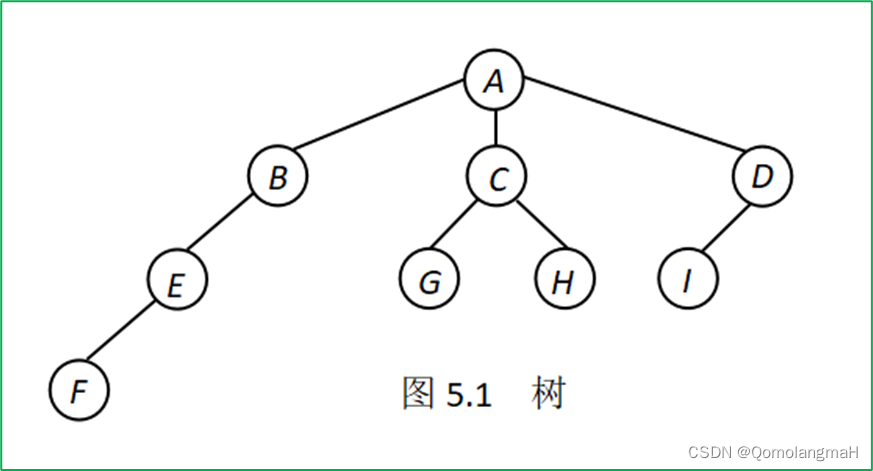
【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
文章目录 5.1 树的基本概念5.1.1 树的定义树有序树、无序树 5.1.2 森林的定义5.1.3 树的术语1. 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(anc…...

2024 Android Framework学习大纲之基础理论篇
2024 Android Framework学习大纲之基础理论篇 受到当前经济影响,互联网越来越不景气了,因此Android App开发也是越来越不景气,中小型公司越来越偏向跨平台开发,比如Flutter,这样能节省成本,笔者也曾经是一名6年多工作经…...

【深度学习】Yolov8 区域计数
git:https://github.com/ultralytics/ultralytics/blob/main/examples/YOLOv8-Region-Counter/readme.md 很长时间没有做yolov的项目了,最近一看yolov8有一个区域计数的功能,不得不说很实用啊。 b站:https://www.bilibili.com/vid…...
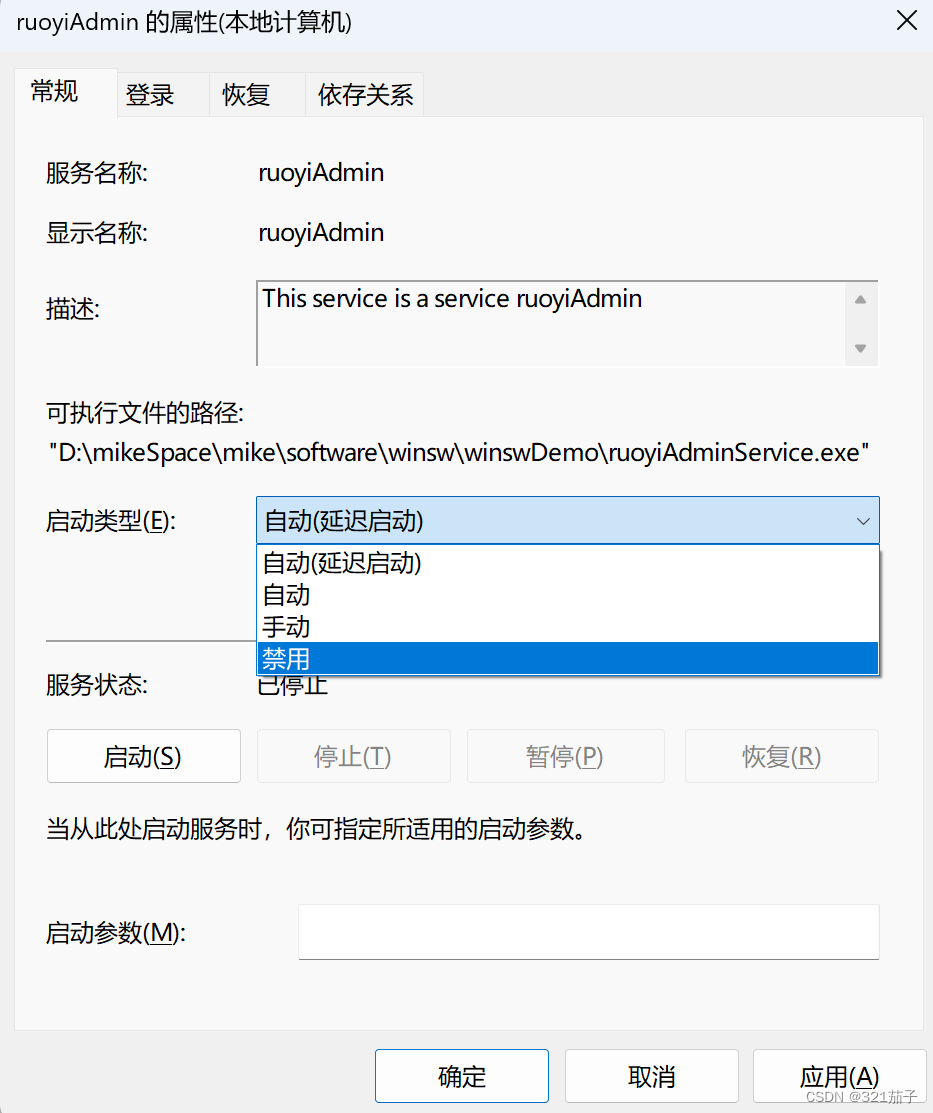
Windows 系统服务器部署jar包时,推荐使用winsw,将jar包注册成服务,并设置开机启动。
一、其他方式不推荐的原因 1、Spring Boot生成的jar包,可以直接用java -jar运行,但是前提是需要登录用户,而且注销用户后会退出程序,所以不可用。 2、使用计划任务,写一个bat处理文件,里面写java -jar运行…...

npm 包管理
1. 命令 // 查看是否登录 npm who am i // 登录:输入用户名、密码、邮箱、一次性登录密码(邮箱接收) npm login // 创建 npm init // 快速创建 npm init -y // 发包 npm publish // 发包(开源) npm publish --access …...
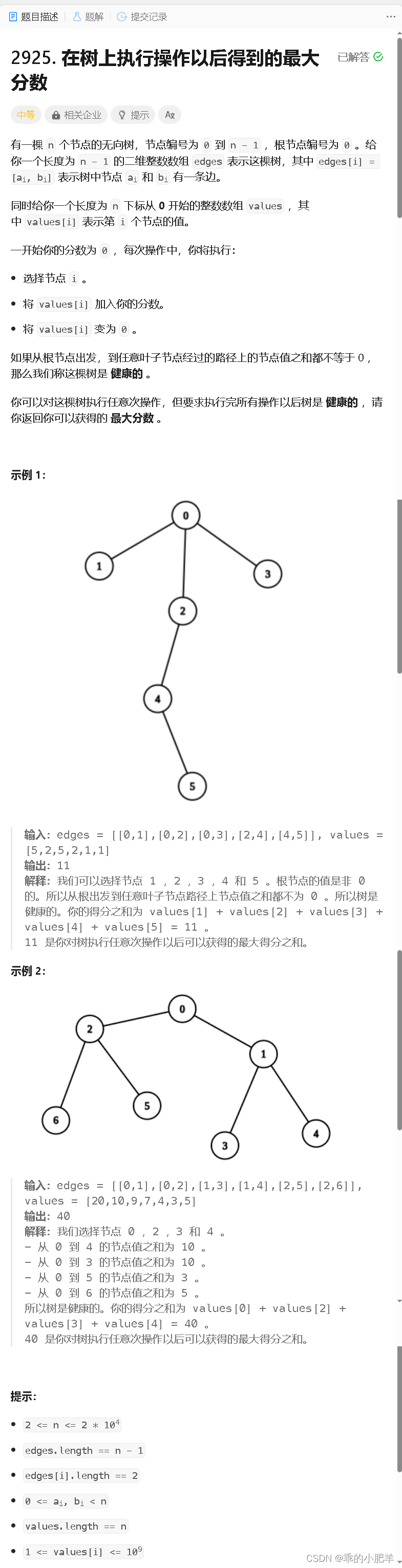
力扣370周赛 -- 第三题(树形DP)
该题的方法,也有点背包的意思,如果一些不懂的朋友,可以从背包的角度去理解该树形DP 问题 题解主要在注释里 //该题是背包问题树形dp问题的结合版,在树上解决背包问题 //背包问题就是选或不选当前物品 //本题求的是最大分数 //先转…...

GPT学习笔记
百度的文心一言 阿里的通义千问 通过GPT能力,提升用户体验和产品力 GPT的出现是AI的iPhone时刻。2007年1月9日,第一代iPhone发布,开启移动互联网时代。新一轮的产业革命。 GPT模型发展时间线: Copilot - 副驾驶 应用…...
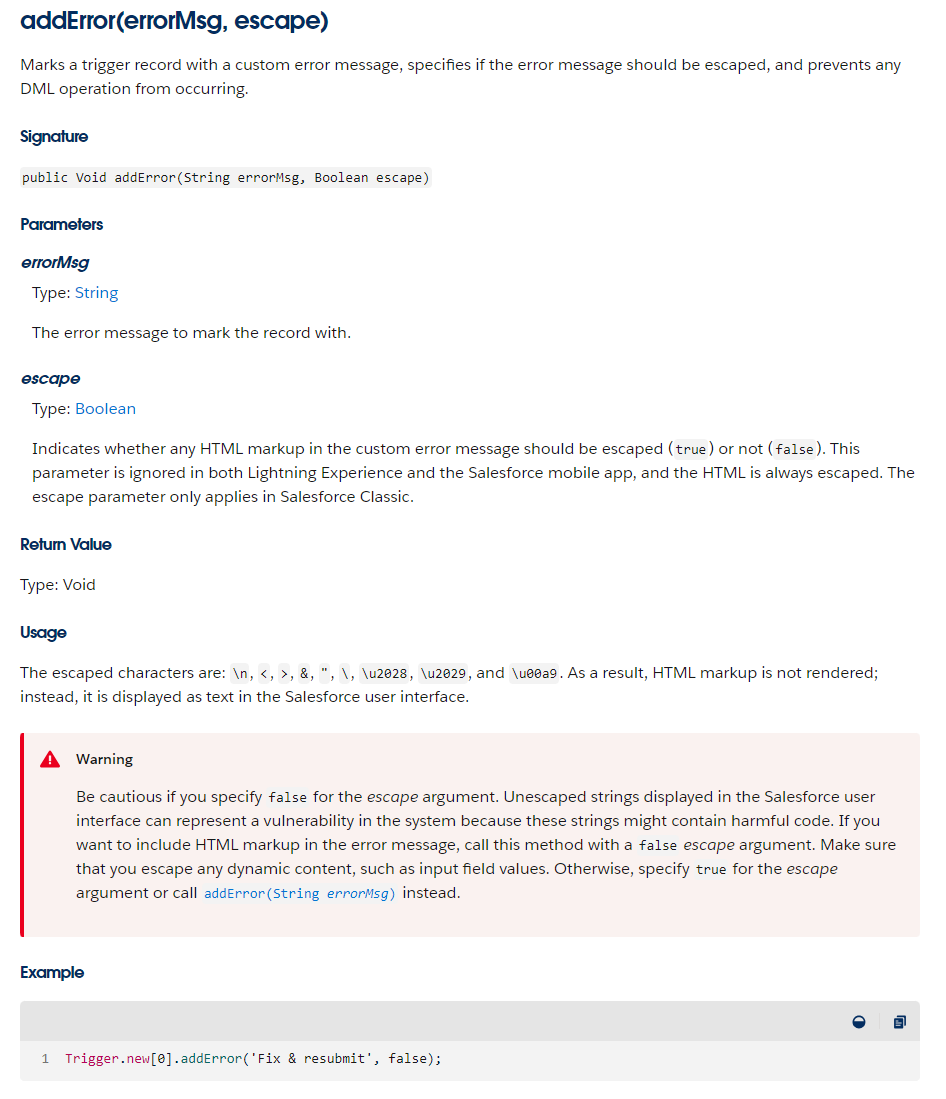
Apex的addError()显示的消息中实现换行
直接用‘<br/>’是无效的,因为addError默认不转义HTML符号,如果需要转义,应该将第二个参数escape设置为false。不过即使设置了也只对classic页面生效,lightning页面还是无法转义。 官方文档: 参考资料…...

STM32中微秒延时的实现方式
STM32中微秒延时的实现方式 0.前言一、裸机实现方式二、FreeRTOS实现方式三、定时器实现(通用)4、总结 0.前言 最近在STM32驱动移植过程中需要用到微秒延时来实现一些外设的时序,由于网上找到的驱动方法良莠不齐,笔者在实现时序过…...
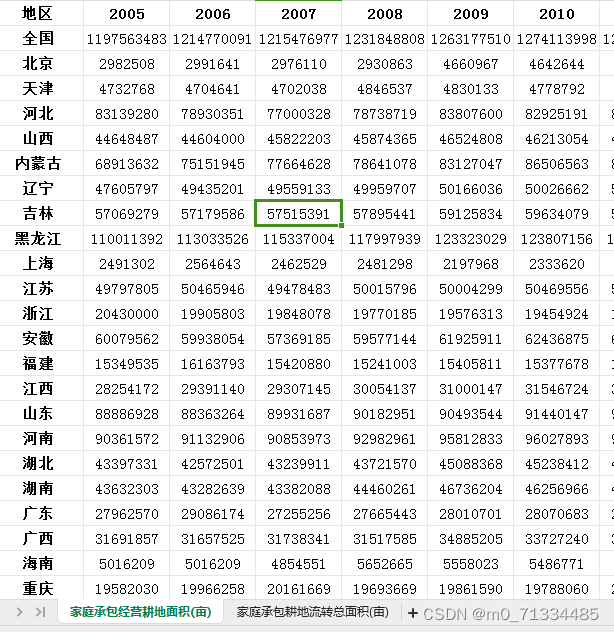
2005-2021年全国各省家庭承包耕地面积和家庭承包耕地流转总面积数据(无缺失)
2005-2021年全国各省家庭承包耕地面积和家庭承包耕地流转总面积数据 1、时间:2005-2021年 2、来源:农村经营管理统计NB 3、指标:家庭承包经营耕地面积、家庭承包耕地流转总面积(单位:亩) 4、范围&#…...
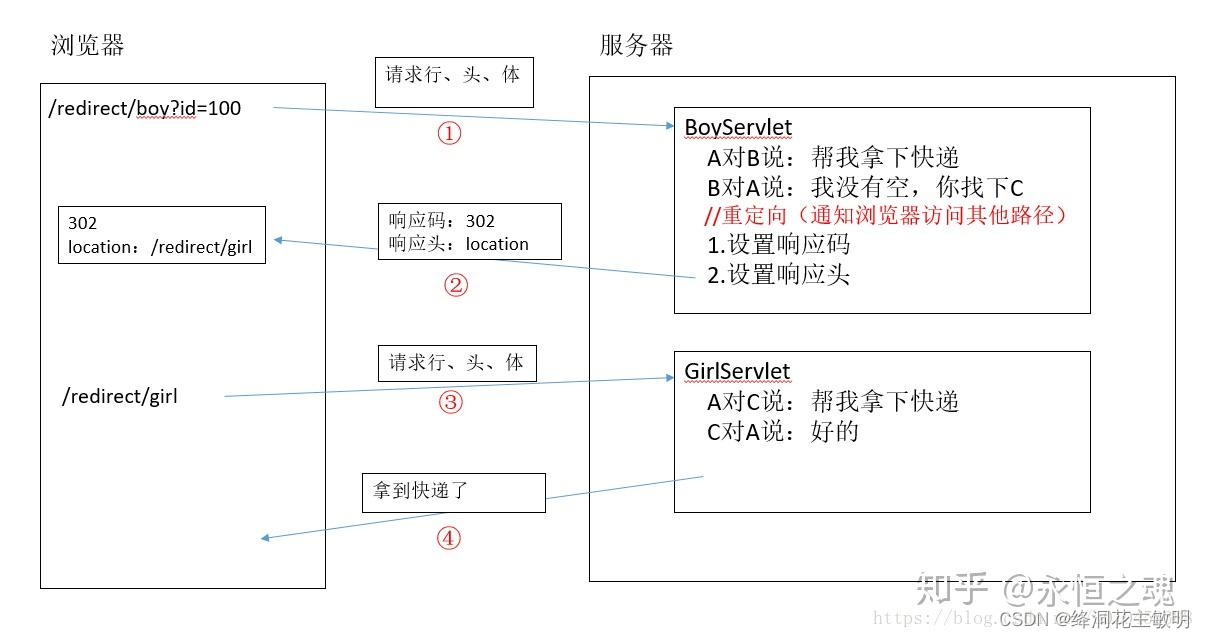
【六、http】go的http的客户端重定向
一、http的重定向 重定向过程:客户浏览器发送http请求----》web服务器接受后发送302状态码响应及对应新的location给客户浏览器–》客户浏览器发现是302响应,则自动再发送一个新的http请求,请求url是新的location地址----》服务器根据此请求寻…...

AI:61-基于深度学习的草莓病害识别
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌在这个漫长的过程,中途遇到了不少问题,但是…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
