【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
文章目录
- 5.1 树的基本概念
- 5.1.1 树的定义
- 树
- 有序树、无序树
- 5.1.2 森林的定义
- 5.1.3 树的术语
- 1. 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(ancestor)
- 2. 度(degree)、叶子节点(leaf node)、分支节点(internal node)
- 3. 结点的层数
- 4. 路径、路径长度、结点的深度、树的深度
- 5.1.4 树的表示
- 1.树形表示法
- 2.嵌套集合表示法
- 3.嵌套括号表示法
- 4.凹入表示法
5.1 树的基本概念
5.1.1 树的定义
树
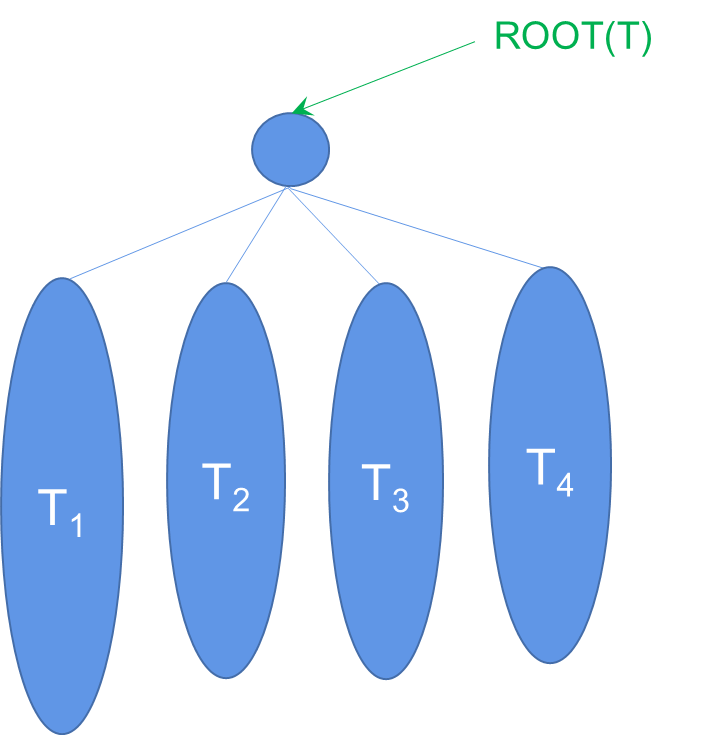
- 一棵树是结点的有限集合T:
- 若T非空,则:
- 有一个特别标出的结点,称作该树的根,记为root(T);
- 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0),其中T1, T2, …, Tm又都是树,称作root(T)的子树。
- T 空时为空树,记作root(T)=NULL。
- 若T非空,则:
有序树、无序树
如果子树T1, T2, …, Tm 的相对次序被指明,则称该树为有序树,否则称为无序树。
在有序树中,把Ti (1≤i≤m)称作根的第 i 个子树。因为计算机表示定义了树的一种隐含次序,所以大多数情况下假定所讨论的树都是有序的,除非另有说明。
- 如果是有序树,那么两者是不同的;如果是无序树,那么两者是相同的。
5.1.2 森林的定义
一个森林是0棵或多棵不相交(非空)树的集合,通常是一个有序的集合。换句话说,森林由多个树组成,这些树之间没有交集,且可以按照一定的次序排列。在森林中,每棵树都是独立的,具有根节点和子树,树与树之间没有直接的连接关系。
森林是树的扩展概念,它是由多个树组成的集合。在计算机科学中,森林也被广泛应用于数据结构和算法设计中,特别是在图论和网络分析等领域。
5.1.3 树的术语
1. 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(ancestor)
-
这些术语用于描述节点之间的关系和层次结构:
- 每个节点都是它的子树的根节点的父亲。
- 反过来,每个节点都是它父亲的儿子。
- 具有相同父亲的节点称为兄弟。
- 每个节点都是它子树中所有节点的祖先。
- 反过来,每个节点都是它祖先的后裔。
-
节点之间的父子关系和兄弟关系可以帮助我们理解树的结构和遍历算法。
-
祖先和后裔的概念则用于描述节点之间的历史关系和衍生关系。
2. 度(degree)、叶子节点(leaf node)、分支节点(internal node)
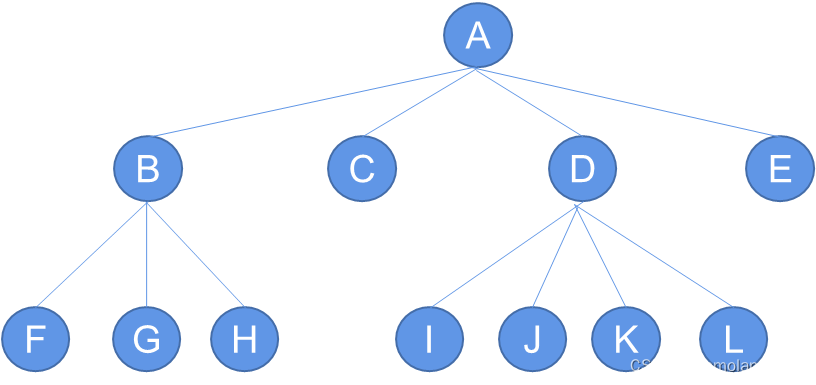
- 一个节点的儿子的个数称为该节点的度或次数。
- 如果一个节点的度为0,则它被称为终端节点或叶子节点(在严格意义上,非根的终端节点称为叶子节点)。
- 非终端节点称为分支节点。
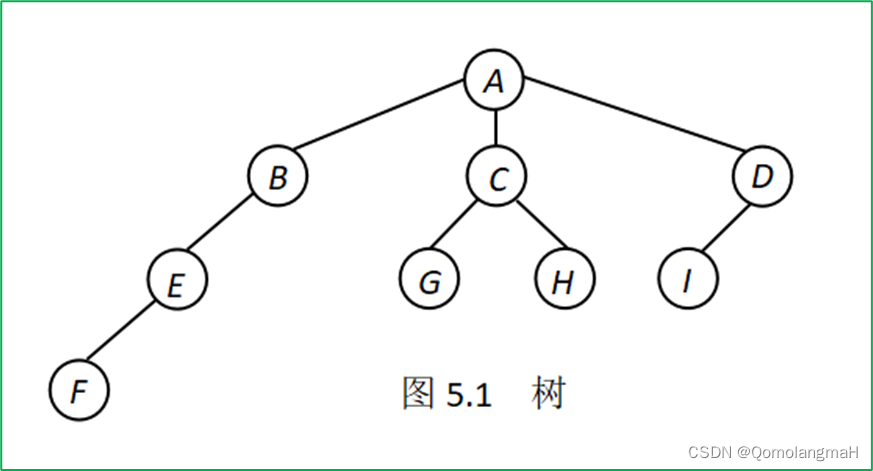
在图5.1中,节点B有一个子树,其度为1;节点A有三个子树,其度为3;因此,这棵树的度为3,可以称为3元树(3-ary tree)。叶子节点是度为0的节点,例如在图5.1中,节点F、G、H和I是叶子节点,而节点A、B、C、D和E是分支节点。
3. 结点的层数
- 结点的层数是根据递归定义来确定的:
- 根节点的层数为0。
- 其余节点的层数是其父节点的层数加1。
- 根节点位于第0层,它的子节点位于第1层,子节点的子节点位于第2层,依此类推。
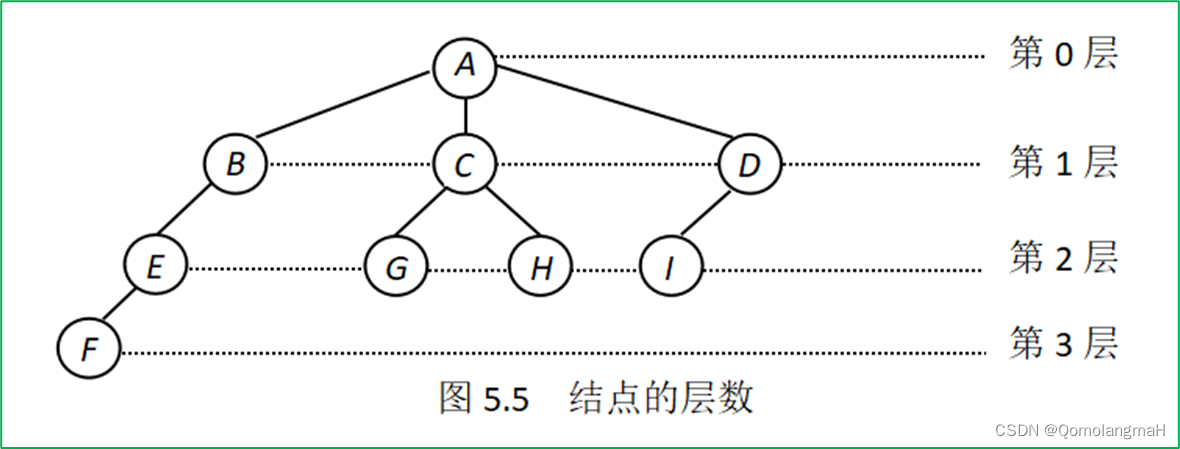
4. 路径、路径长度、结点的深度、树的深度
- 路径是指结点序列v1, v2, …, vk,其中每个节点vi是节点vi+1的父节点(1 ≤ i < k)。
- 路径长度是指路径经过的边数,即k-1。
- 结点vi的深度是指从根节点到结点vi的路径长度 D e p t h ( i ) Depth(i) Depth(i)。
- 一棵树的深度是指树中所有节点深度的最大值: m a x i = 1 , … , n D e p t h ( i ) max_{i=1,…, n}Depth(i) maxi=1,…,nDepth(i)

图5.1的树中,结点序列A, B, E是结点A到结点E的路径,路经长度为2,结点E的深度为2,树的深度为3。
5.1.4 树的表示
- 可参照:【数据结构】树与二叉树(二):树的表示C语言:树形表示法、嵌套集合表示法、嵌套括号表示法 、凹入表示法
- 关于树(二叉树)的基础操作有待进一步更新~
1.树形表示法
树形表示法是一种图形化的表示方法,使用节点和边来表示树的结构。每个节点代表树中的一个元素,而边表示节点之间的关系。这种表示方法可以直观地展示树的层次结构和节点之间的连接关系。
python创建树:
class TreeNode:def __init__(self, value):self.value = valueself.children = []# 创建一个树
root = TreeNode('A')
node1 = TreeNode('B')
node2 = TreeNode('C')
node3 = TreeNode('D')root.children.append(node1)
root.children.append(node2)
node2.children.append(node3)
2.嵌套集合表示法
tree = {'value': 'A','children': [{'value': 'B','children': []},{'value': 'C','children': [{'value': 'D','children': []}]}]
}
3.嵌套括号表示法
tree_str = '((A (B C)) D)'
4.凹入表示法
def print_tree(node, level=0):if node is None:returnprint(' ' * level + str(node.value))for child in node.children:print_tree(child, level + 1)print_tree(root)
相关文章:

【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
文章目录 5.1 树的基本概念5.1.1 树的定义树有序树、无序树 5.1.2 森林的定义5.1.3 树的术语1. 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(anc…...

2024 Android Framework学习大纲之基础理论篇
2024 Android Framework学习大纲之基础理论篇 受到当前经济影响,互联网越来越不景气了,因此Android App开发也是越来越不景气,中小型公司越来越偏向跨平台开发,比如Flutter,这样能节省成本,笔者也曾经是一名6年多工作经…...

【深度学习】Yolov8 区域计数
git:https://github.com/ultralytics/ultralytics/blob/main/examples/YOLOv8-Region-Counter/readme.md 很长时间没有做yolov的项目了,最近一看yolov8有一个区域计数的功能,不得不说很实用啊。 b站:https://www.bilibili.com/vid…...
Windows 系统服务器部署jar包时,推荐使用winsw,将jar包注册成服务,并设置开机启动。
一、其他方式不推荐的原因 1、Spring Boot生成的jar包,可以直接用java -jar运行,但是前提是需要登录用户,而且注销用户后会退出程序,所以不可用。 2、使用计划任务,写一个bat处理文件,里面写java -jar运行…...

npm 包管理
1. 命令 // 查看是否登录 npm who am i // 登录:输入用户名、密码、邮箱、一次性登录密码(邮箱接收) npm login // 创建 npm init // 快速创建 npm init -y // 发包 npm publish // 发包(开源) npm publish --access …...
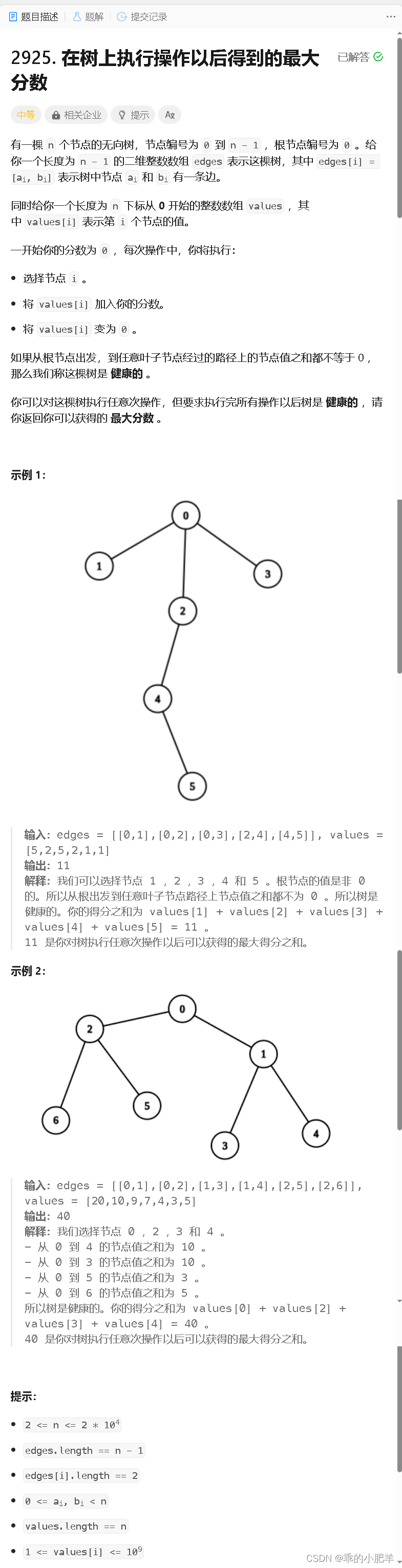
力扣370周赛 -- 第三题(树形DP)
该题的方法,也有点背包的意思,如果一些不懂的朋友,可以从背包的角度去理解该树形DP 问题 题解主要在注释里 //该题是背包问题树形dp问题的结合版,在树上解决背包问题 //背包问题就是选或不选当前物品 //本题求的是最大分数 //先转…...

GPT学习笔记
百度的文心一言 阿里的通义千问 通过GPT能力,提升用户体验和产品力 GPT的出现是AI的iPhone时刻。2007年1月9日,第一代iPhone发布,开启移动互联网时代。新一轮的产业革命。 GPT模型发展时间线: Copilot - 副驾驶 应用…...
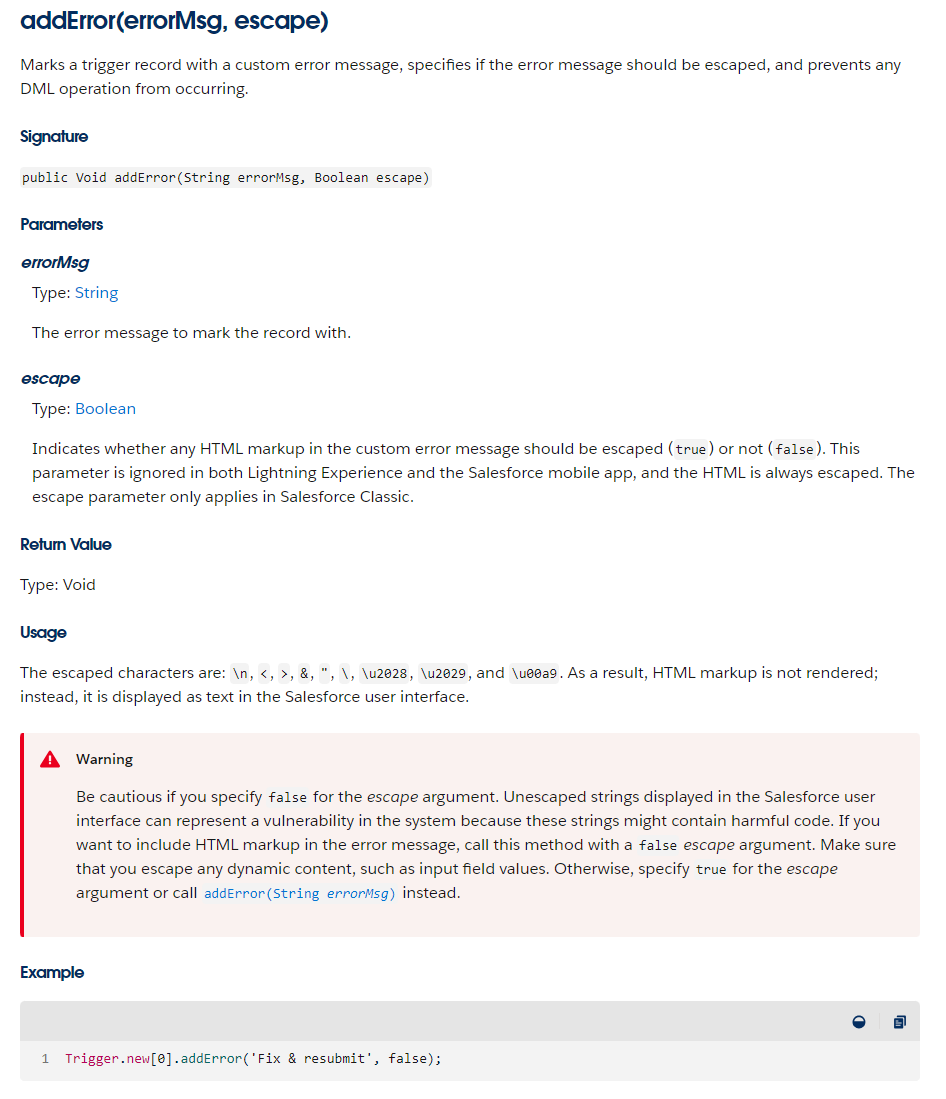
Apex的addError()显示的消息中实现换行
直接用‘<br/>’是无效的,因为addError默认不转义HTML符号,如果需要转义,应该将第二个参数escape设置为false。不过即使设置了也只对classic页面生效,lightning页面还是无法转义。 官方文档: 参考资料…...

STM32中微秒延时的实现方式
STM32中微秒延时的实现方式 0.前言一、裸机实现方式二、FreeRTOS实现方式三、定时器实现(通用)4、总结 0.前言 最近在STM32驱动移植过程中需要用到微秒延时来实现一些外设的时序,由于网上找到的驱动方法良莠不齐,笔者在实现时序过…...
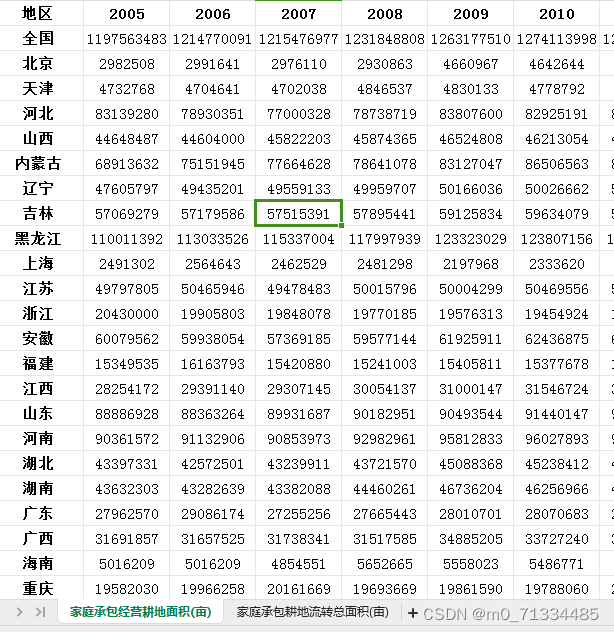
2005-2021年全国各省家庭承包耕地面积和家庭承包耕地流转总面积数据(无缺失)
2005-2021年全国各省家庭承包耕地面积和家庭承包耕地流转总面积数据 1、时间:2005-2021年 2、来源:农村经营管理统计NB 3、指标:家庭承包经营耕地面积、家庭承包耕地流转总面积(单位:亩) 4、范围&#…...
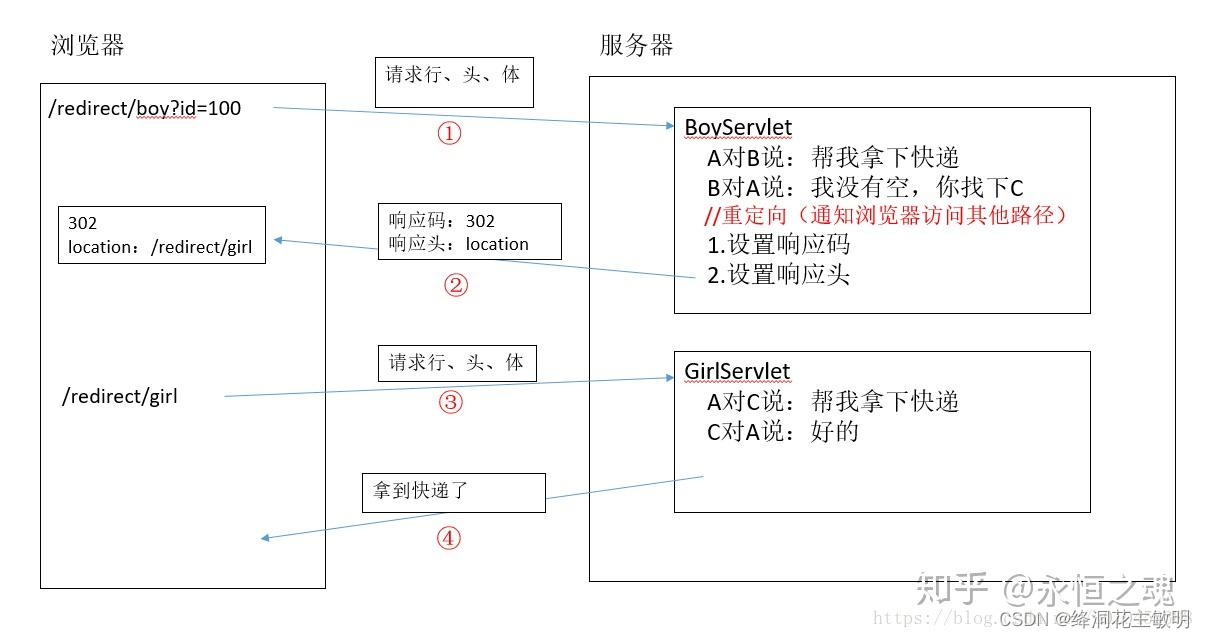
【六、http】go的http的客户端重定向
一、http的重定向 重定向过程:客户浏览器发送http请求----》web服务器接受后发送302状态码响应及对应新的location给客户浏览器–》客户浏览器发现是302响应,则自动再发送一个新的http请求,请求url是新的location地址----》服务器根据此请求寻…...

AI:61-基于深度学习的草莓病害识别
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌在这个漫长的过程,中途遇到了不少问题,但是…...
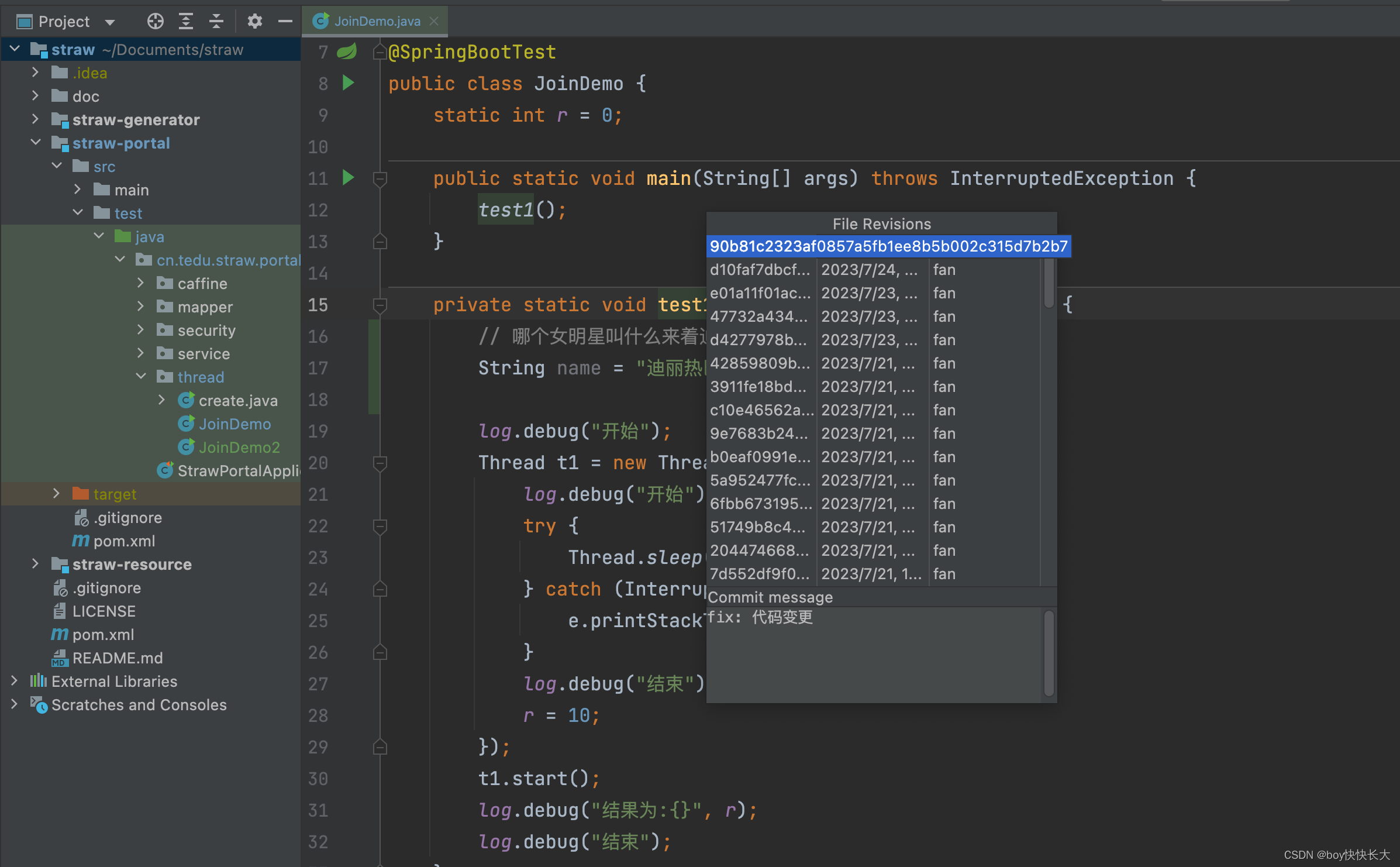
idea文件比对
idea文件比对 1.项目内的文件比对2.项目间的文件比对3. 剪切板对比4. 版本历史(不同分支和不同commit)对比 1.项目内的文件比对 在项目中选择好需要比对的文件(类),然后选择Compare Files Mac下的快捷键是Commandd, 这样的比对像是git冲突解决一样 …...
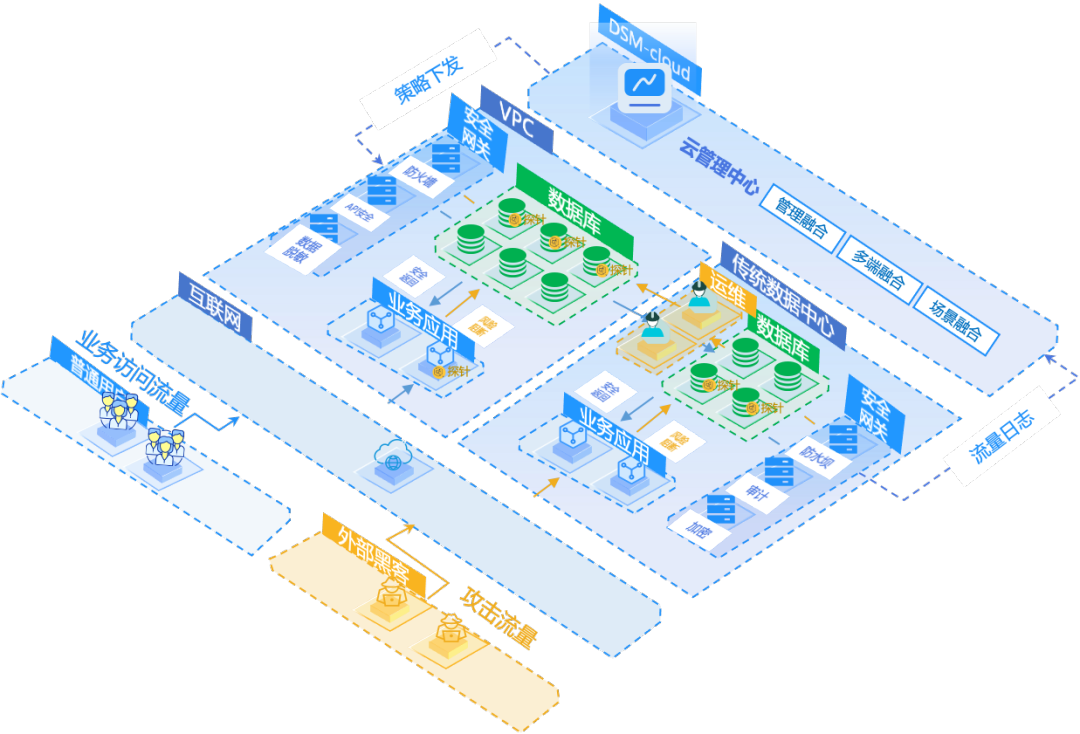
重磅发布|美创科技新一代 数据安全管理平台(DSM Cloud)全新升级
重磅发布 新一代 数据安全管理平台(DSM Cloud) 美创科技新一代 数据安全管理平台(简称:DSM Cloud)全新升级,正式发布。 在业务上云飞速发展过程中,快速应对数据激增,同时有效保障数…...
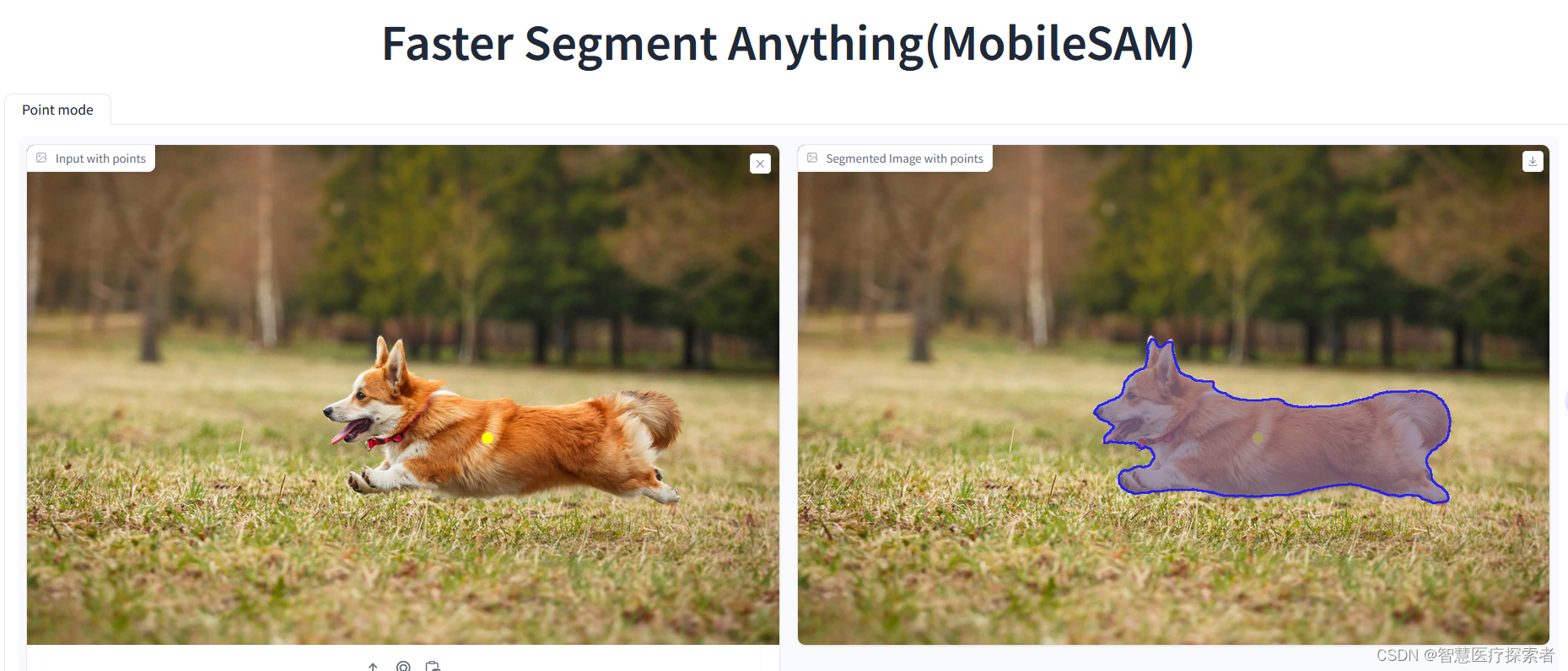
比SAM小60倍的分割一切模型:MobileSAM
1 MobileSAM SAM就是一类处理图像分割任务的通用模型。与以往只能处理某种特定类型图片的图像分割模型不同,SAM可以处理所有类型的图像。 在SAM出现前,基本上所有的图像分割模型都是专有模型。比如,在医学领域,有专门分割核磁图…...
版本控制系统-SVN
SVN Apache Subversion 通常被缩写成 SVN,是一个开放源代码的版本控制系统。 官网:https://subversion.apache.org 资料:https://svnbook.red-bean.com、https://www.runoob.com/svn/svn-tutorial.html 下载:https://sourceforg…...

【电路笔记】-串联RLC电路分析
串联RLC电路分析 文章目录 串联RLC电路分析1、概述2、瞬态响应3、AC响应4、RCL和CLR配置5、结论 电阻器 、电感器 (L) 和电容器 © 是电子器件中的三个基本无源元件。 它们的属性和行为已在交流电阻、交流电感和交流电容文章中详细介绍。 在本文中,我们将重点讨…...

大数据毕业设计选题推荐-家具公司运营数据分析平台-Hadoop-Spark-Hive
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...

【触想智能】工业显示器上市前的检测项目分享
工业显示器在上市前,需要做一项重要的工作,那就是工业显示器出厂前的产品可靠性检测。 工业显示器选择的测试项目相比商用端更为严格,常见的性能测试项目包括高温老化、防尘防水、电磁静电干扰、防摔防撞等,在工业级应用领域&…...

Vue使用epubjs电子书
npmjs: https://www.npmjs.com/package/epubjs 在线电子书转换器 安装: npm i epubjs 简单封装: src/hooks/ import Epub from "epubjs"; import type { Book, Rendition } from epubjs import type { BookOptions } from epubjs/types…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...