基于前馈神经网络完成鸢尾花分类
目录
1 小批量梯度下降法
1.0 展开聊一聊~
1.1 数据分组
1.2 用DataLoader进行封装
1.3 模型构建
1.4 完善Runner类
1.5 模型训练
1.6 模型评价
1.7 模型预测
思考
总结
参考文献
首先基础知识铺垫~
继续使用第三章中的鸢尾花分类任务,将Softmax分类器替换为前馈神经网络。
- 损失函数:交叉熵损失;
- 优化器:随机梯度下降法;
- 评价指标:准确率;
1 小批量梯度下降法
1.0 展开聊一聊~
在梯度下降法中,目标函数是整个训练集上的风险函数,这种方式称为批量梯度下降法(Batch Gradient Descent,BGD)。批量梯度下降法在每次迭代时需要计算每个样本上损失函数的梯度并求和。为了减少每次迭代的计算复杂度,我们可以在每次迭代时只采集一小部分样本,计算在这组样本上损失函数的梯度并更新参数,这种优化方式称为小批量梯度下降法(Mini-Batch Gradient Descent,Mini-Batch GD)。
梯度下降算法一般情况下主要说的是三种,批量梯度下降、随机梯度下降、小批量梯度下降。
知道大家跟我一样不爱看一大段一大段的定义,巴拉巴拉一堆的,所以我大概总结了一下,快拿出你们的小本本!!!
首先,要明确梯度下降算法都是优化算法,用于求解目标函数的最优参数:
- 批量梯度下降(Batch Gradient Descent,BGD)
- 随机梯度下降(Stochastic Gradient Descent,SGD)
- 小批量梯度下降(Mini-Batch Gradient Descent,MBGD)
批量梯度下降(BGD):最早出现的梯度下降方法是批量梯度下降。BGD在每一次迭代中使用所有训练样本来计算梯度,并更新模型参数,步骤如下:
- 对于每个训练样本,计算梯度。
- 将所有梯度求平均,得到一个全局梯度。
- 根据学习率和全局梯度更新模型参数。
优点:
- 收敛性较好,能够达到全局最优(目标函数是凸函数)。
- 梯度计算相对准确,参数更新稳定。
- 收敛速度最快,可以保证每一步都是准确地向着极值点的方向趋近,所需要的迭代次数最少。
缺点:
- 计算梯度时需要处理大量数据,计算开销较大。
- 参数更新只能在整个训练集上进行,但大规模数据集通常会有大量冗余数据,所以不适用于大规模数据集。
- 容易陷入局部最优(目标函数是非凸函数)。
这里需要提一下~对所有样本的计算,可以利用向量运算进行并行计算来提升运算速度。
随机梯度下降(SGD):为了解决批量梯度下降在处理大规模数据集时的计算开销问题,随机梯度下降方法被提出。SGD在每一次迭代中仅使用一个训练样本来计算梯度,并更新模型参数。具体步骤如下:
- 随机选择一个训练样本。
- 计算该样本的梯度。
- 根据学习率和该样本的梯度更新模型参数。
优点:
- 计算开销较小,适用于大规模数据集。
- 参数更新频繁,可能更容易逃离局部最优。
缺点:
- 每次迭代只使用一个样本,但是单个样本计算出的梯度不能够很好的体现全体样本的梯度。
- 参数更新的方向较不稳定,可能会产生参数震荡。
- 参数更新非常的频繁,在最优点附近晃来晃去,收敛速度大大降低。
小批量梯度下降(MBGD):为了兼顾批量梯度下降和随机梯度下降的优点,小批量梯度下降方法被引入。小批量梯度下降算法又被叫做小批量随机梯度下降算法。MBGD在每一次迭代中使用一小部分训练样本(通常称为mini-batch)来计算梯度,并更新模型参数。具体步骤如下:
- 随机选择一小部分训练样本(mini-batch)。
- 计算这些样本的梯度。
- 根据学习率和这些样本的梯度更新模型参数。
优点:
- 兼具BGD和SGD的优点,计算开销适中,参数更新相对稳定。
- 可以利用矩阵运算的高效性,提高计算效率。
- 较容易并行化处理,适用于大规模数据集。
缺点:
- 学习率选择较为敏感,需要进行合适的调参。
总结:三种梯度下降方法各有优劣。批量梯度下降收敛性好,但计算开销大;随机梯度下降计算开销小,但更新不稳定;小批量梯度下降在两者之间取得平衡,并且对于大规模数据集有较好的适应性。在实际应用中,根据具体问题的规模和特点选择合适的梯度下降方法。
1.1 数据分组
为了小批量梯度下降法,我们需要对数据进行随机分组。目前,机器学习中通常做法是构建一个数据迭代器,每个迭代过程中从全部数据集中获取一批指定数量的数据。原理图展示一下:
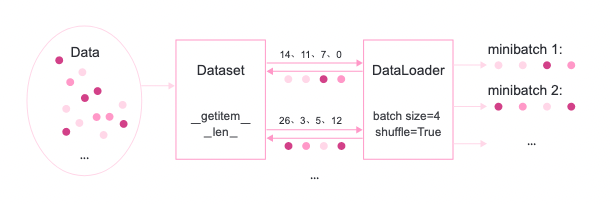
首先,将数据集封装为Dataset类,传入一组索引值,根据索引从数据集合中获取数据;
其次,构建DataLoader类,需要指定数据批量的大小和是否需要对数据进行乱序,通过该类即可批量获取数据。
import torch.utils.data as Dataclass IrisDataset(Data.Dataset):def __init__(self, mode='train', num_train=120, num_dev=15):super(IrisDataset, self).__init__()# 调用第三章中的数据读取函数,其中不需要将标签转成one-hot类型X, y = load_data(shuffle=True)if mode == 'train':self.X, self.y = X[:num_train], y[:num_train]elif mode == 'dev':self.X, self.y = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]else:self.X, self.y = X[num_train + num_dev:], y[num_train + num_dev:]def __getitem__(self, idx):return self.X[idx], self.y[idx]def __len__(self):return len(self.y)__getitem__:根据给定索引获取数据集中指定样本,并对样本进行数据处理;
__len__:返回数据集样本个数。
train_dataset = IrisDataset(mode='train')
dev_dataset = IrisDataset(mode='dev')
test_dataset = IrisDataset(mode='test')print("length of train set: ", len(train_dataset)) ![]()
1.2 用DataLoader进行封装
batch_size = 16# 加载数据
train_loader = Data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = Data.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = Data.DataLoader(test_dataset, batch_size=batch_size)1.3 模型构建
class Model_MLP_L2_V3(nn.Module):def __init__(self, input_size, output_size, hidden_size):super(Model_MLP_L2_V3, self).__init__()# 构建第一个全连接层self.fc1 = nn.Linear(input_size, hidden_size)# 构建第二全连接层self.fc2 = nn.Linear(hidden_size, output_size)# 定义网络使用的激活函数self.act = nn.Sigmoid()nn.init.normal_(self.fc1.weight, mean=0., std=0.01)nn.init.constant_(self.fc1.bias, 1.0)nn.init.normal_(self.fc2.weight, mean=0., std=0.01)nn.init.constant_(self.fc2.bias, 1.0)def forward(self, inputs):outputs = self.fc1(inputs)outputs = self.act(outputs)outputs = self.fc2(outputs)return outputsfnn_model = Model_MLP_L2_V3(input_size=4, output_size=3, hidden_size=6)1.4 完善Runner类
class Accuracy(object):def __init__(self, is_logist=True):"""输入:- is_logist: outputs是logist还是激活后的值"""# 用于统计正确的样本个数self.num_correct = 0# 用于统计样本的总数self.num_count = 0self.is_logist = is_logistdef update(self, outputs, labels):"""输入:- outputs: 预测值, shape=[N,class_num]- labels: 标签值, shape=[N,1]"""# 判断是二分类任务还是多分类任务,shape[1]=1时为二分类任务,shape[1]>1时为多分类任务if outputs.shape[1] == 1: # 二分类outputs = torch.squeeze(outputs, axis=-1)if self.is_logist:# logist判断是否大于0preds = (outputs >= 0).to(torch.float32)else:# 如果不是logist,判断每个概率值是否大于0.5,当大于0.5时,类别为1,否则类别为0preds = (outputs >= 0.5).to(torch.float32)else:# 多分类时,使用'paddle.argmax'计算最大元素索引作为类别preds = torch.argmax(outputs, dim=1).int()# 获取本批数据中预测正确的样本个数labels = torch.squeeze(labels, dim=-1)batch_correct = float((preds == labels).sum())# batch_correct = torch.sum(torch.tensor(preds == labels, dtype=torch.float32)).numpy()batch_count = len(labels)# 更新num_correct 和 num_countself.num_correct += batch_correctself.num_count += batch_countdef accumulate(self):# 使用累计的数据,计算总的指标if self.num_count == 0:return 0return self.num_correct / self.num_countdef reset(self):# 重置正确的数目和总数self.num_correct = 0self.num_count = 0def name(self):return "Accuracy"完善RunnerV3类
import torchclass RunnerV3(object):def __init__(self, model, optimizer, loss_fn, metric, **kwargs):self.model = modelself.optimizer = optimizerself.loss_fn = loss_fnself.metric = metric # 只用于计算评价指标# 记录训练过程中的评价指标变化情况self.dev_scores = []# 记录训练过程中的损失函数变化情况self.train_epoch_losses = [] # 一个epoch记录一次lossself.train_step_losses = [] # 一个step记录一次lossself.dev_losses = []# 记录全局最优指标self.best_score = 0def train(self, train_loader, dev_loader=None, **kwargs):# 将模型切换为训练模式self.model.train()# 传入训练轮数,如果没有传入值则默认为0num_epochs = kwargs.get("num_epochs", 0)# 传入log打印频率,如果没有传入值则默认为100log_steps = kwargs.get("log_steps", 100)# 评价频率eval_steps = kwargs.get("eval_steps", 0)# 传入模型保存路径,如果没有传入值则默认为"best_model.pdparams"save_path = kwargs.get("save_path", "best_model.pdparams")custom_print_log = kwargs.get("custom_print_log", None)# 训练总的步数num_training_steps = num_epochs * len(train_loader)if eval_steps:if self.metric is None:raise RuntimeError('Error: Metric can not be None!')if dev_loader is None:raise RuntimeError('Error: dev_loader can not be None!')# 运行的step数目global_step = 0# 进行num_epochs轮训练for epoch in range(num_epochs):# 用于统计训练集的损失total_loss = 0for step, data in enumerate(train_loader):X, y = data# 获取模型预测logits = self.model(X)loss = self.loss_fn(logits, y) # 默认求meantotal_loss += loss# 训练过程中,每个step的loss进行保存self.train_step_losses.append((global_step, loss.item()))if log_steps and global_step % log_steps == 0:print(f"[Train] epoch: {epoch}/{num_epochs}, step: {global_step}/{num_training_steps}, loss: {loss.item():.5f}")# 梯度反向传播,计算每个参数的梯度值loss.backward()if custom_print_log:custom_print_log(self)# 小批量梯度下降进行参数更新self.optimizer.step()# 梯度归零self.optimizer.zero_grad() #无clear_grad# 判断是否需要评价if eval_steps > 0 and global_step > 0 and \(global_step % eval_steps == 0 or global_step == (num_training_steps - 1)):dev_score, dev_loss = self.evaluate(dev_loader, global_step=global_step)print(f"[Evaluate] dev score: {dev_score:.5f}, dev loss: {dev_loss:.5f}")# 将模型切换为训练模式self.model.train()# 如果当前指标为最优指标,保存该模型if dev_score > self.best_score:self.save_model(save_path)print(f"[Evaluate] best accuracy performence has been updated: {self.best_score:.5f} --> {dev_score:.5f}")self.best_score = dev_scoreglobal_step += 1# 当前epoch 训练loss累计值trn_loss = (total_loss / len(train_loader)).item()# epoch粒度的训练loss保存self.train_epoch_losses.append(trn_loss)print("[Train] Training done!")# 模型评估阶段,使用'paddle.no_grad()'控制不计算和存储梯度@torch.no_grad()def evaluate(self, dev_loader, **kwargs):assert self.metric is not None# 将模型设置为评估模式self.model.eval()global_step = kwargs.get("global_step", -1)# 用于统计训练集的损失total_loss = 0# 重置评价self.metric.reset()# 遍历验证集每个批次for batch_id, data in enumerate(dev_loader):X, y = data# 计算模型输出logits = self.model(X)# 计算损失函数loss = self.loss_fn(logits, y).item()# 累积损失total_loss += loss# 累积评价self.metric.update(logits, y)dev_loss = (total_loss / len(dev_loader))dev_score = self.metric.accumulate()# 记录验证集lossif global_step != -1:self.dev_losses.append((global_step, dev_loss))self.dev_scores.append(dev_score)return dev_score, dev_loss# 模型评估阶段,使用'paddle.no_grad()'控制不计算和存储梯度@torch.no_grad()def predict(self, x, **kwargs):# 将模型设置为评估模式self.model.eval()# 运行模型前向计算,得到预测值logits = self.model(x)return logitsdef save_model(self, save_path):torch.save(self.model.state_dict(), save_path)def load_model(self, model_path):model_state_dict = torch.load(model_path)self.model.load_state_dict(model_state_dict)注意torch环境中没有clear_grad方法,这儿需要调用zero_grad方法。
1.5 模型训练
这里把RunnerV3放入runner.py存储在nndl文件夹中
import torch.optim as opt
from nndl.runner import RunnerV3
import torch.nn.functional as Flr = 0.2
# 定义网络
model = fnn_model
# 定义优化器
optimizer = opt.SGD(model.parameters(), lr=lr)
# 定义损失函数。softmax+交叉熵
loss_fn = F.cross_entropy# 定义评价指标
metric = Accuracy(is_logist=True)runner = RunnerV3(model, optimizer, loss_fn, metric)使用训练集和验证集进行模型训练,共训练150个epoch。在实验中,保存准确率最高的模型作为最佳模型。
# 启动训练
log_steps = 100
eval_steps = 50
runner.train(train_loader, dev_loader,num_epochs=150, log_steps=log_steps, eval_steps=eval_steps,save_path="best_model.pdparams")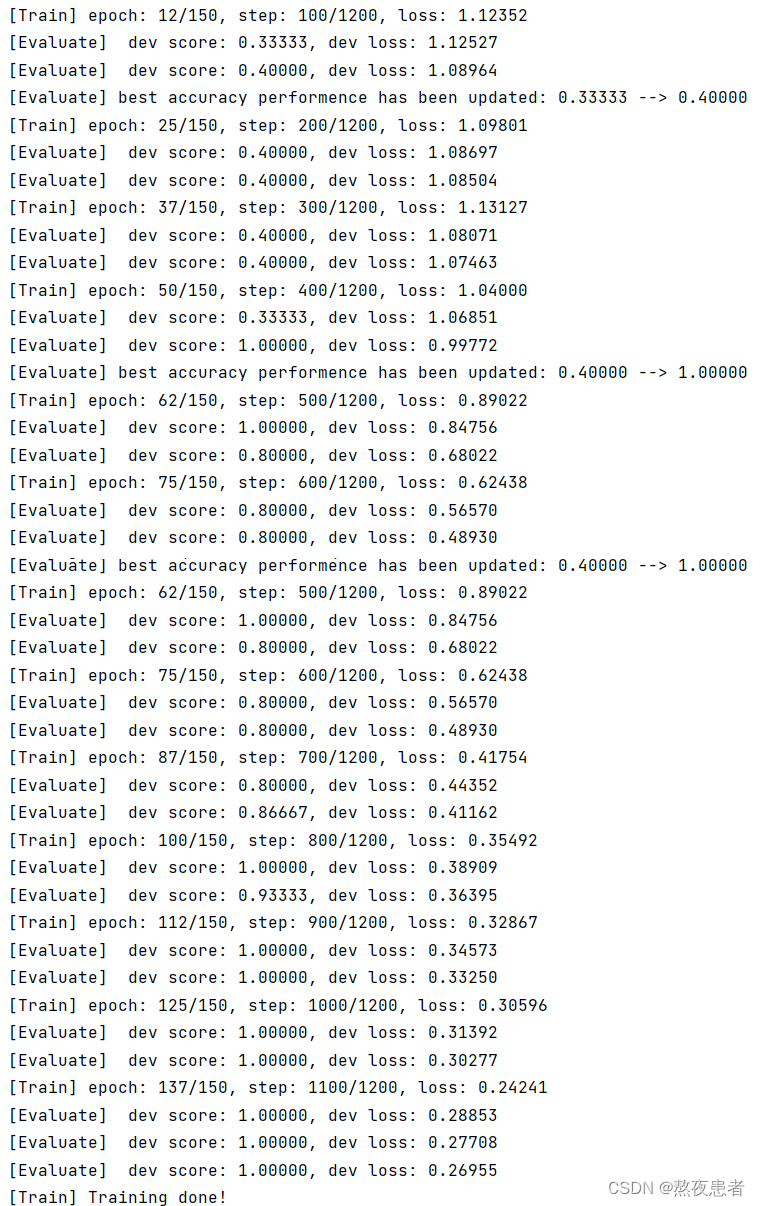
可视化观察训练集损失和训练集loss变化情况,代码如下:
import matplotlib.pyplot as plt# 绘制训练集和验证集的损失变化以及验证集上的准确率变化曲线
def plot_training_loss_acc(runner, fig_name,fig_size=(16, 6),sample_step=20,loss_legend_loc="upper right",acc_legend_loc="lower right",train_color="#e4007f",dev_color='#f19ec2',fontsize='large',train_linestyle="-",dev_linestyle='--'):global dev_stepsplt.figure(figsize=fig_size)plt.subplot(1, 2, 1)train_items = runner.train_step_losses[::sample_step]train_steps = [x[0] for x in train_items]train_losses = [x[1] for x in train_items]plt.plot(train_steps, train_losses, color=train_color, linestyle=train_linestyle, label="Train loss")if len(runner.dev_losses) > 0:dev_steps = [x[0] for x in runner.dev_losses]dev_losses = [x[1] for x in runner.dev_losses]plt.plot(dev_steps, dev_losses, color=dev_color, linestyle=dev_linestyle, label="Dev loss")# 绘制坐标轴和图例plt.ylabel("loss", fontsize=fontsize)plt.xlabel("step", fontsize=fontsize)plt.legend(loc=loss_legend_loc, fontsize='x-large')# 绘制评价准确率变化曲线if len(runner.dev_scores) > 0:plt.subplot(1, 2, 2)plt.plot(dev_steps, runner.dev_scores,color=dev_color, linestyle=dev_linestyle, label="Dev accuracy")# 绘制坐标轴和图例plt.ylabel("score", fontsize=fontsize)plt.xlabel("step", fontsize=fontsize)plt.legend(loc=acc_legend_loc, fontsize='x-large')plt.savefig(fig_name)plt.show()plot_training_loss_acc(runner, 'fw-loss.pdf') 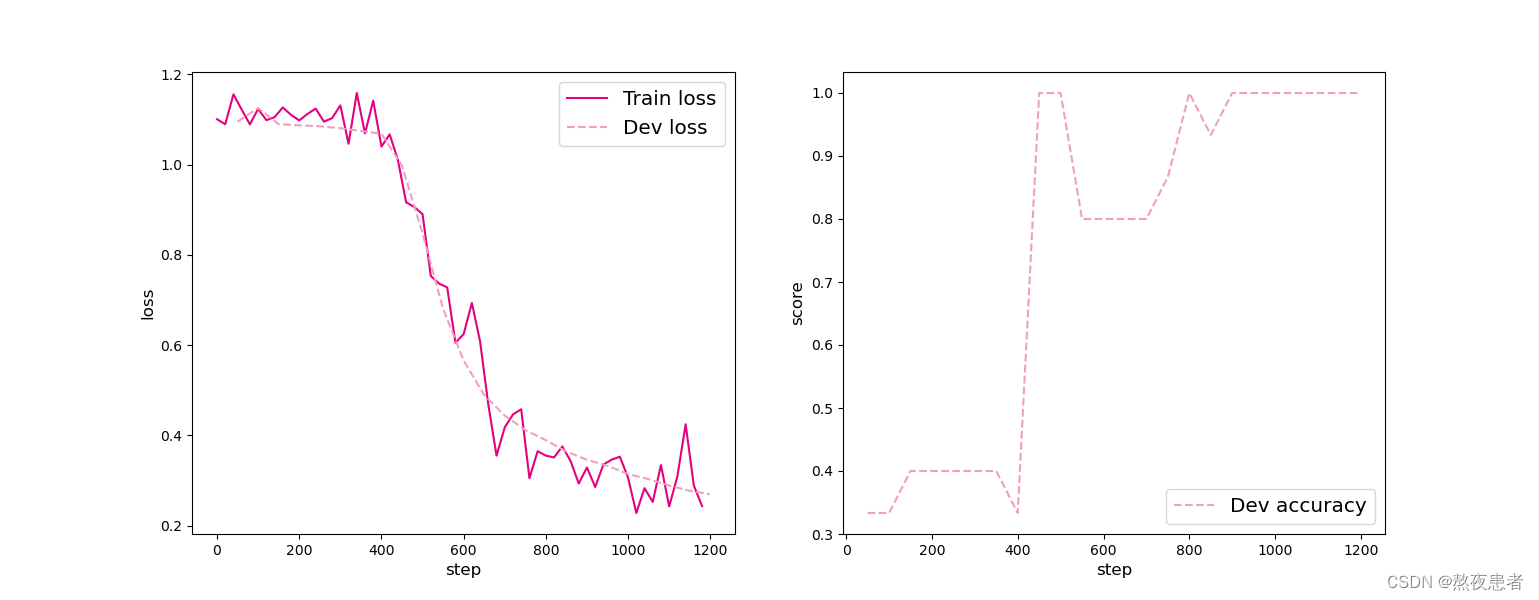
1.6 模型评价
使用测试数据对在训练过程中保存的最佳模型进行评价,观察模型在测试集上的准确率以及Loss情况,代码如下:
# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))![]()
1.7 模型预测
同样地,也可以使用保存好的模型,对测试集中的某一个数据进行模型预测,观察模型效果。代码如下
# 获取测试集中第一条数据
X, label = train_dataset[0]
logits = runner.predict(X)pred_class = torch.argmax(logits[0]).numpy()
label = label.numpy()# 输出真实类别与预测类别
print("The true category is {} and the predicted category is {}".format(label, pred_class))![]()
思考
softmax、svm、前馈神经网络三种进行比较,svm代码如下:
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score
def SVC_split(x_train, y_train, x_test, y_test):# 定义SVM分类器svm = SVC()# 定义参数空间param_grid = {'C': [0.01, 0.1, 1, 10],'kernel': ['linear', 'rbf', 'poly'],'gamma': ['scale', 'auto']}# 使用GridSearchCV进行交叉验证和参数选择grid_search = GridSearchCV(svm, param_grid=param_grid, cv=5)grid_search.fit(x_train, y_train.ravel())# 在测试集上评估模型性能y_pred = grid_search.predict(x_test)accuracy = accuracy_score(y_test, y_pred)print("Accuracy on test set: {:.2f}%".format(accuracy * 100))SVC_split(train_dataset.X,train_dataset.y ,test_dataset.X, test_dataset.y)![]()
调用实验四的softmax函数的结果如下:
![]()
很明显我们发现softmax回归的准确率远远低于前馈神经网络和svm,简单总结一下都有什么原因吧:
softmax回归是一个线性模型,其只能学习到线性关系。对于复杂的非线性分类问题,Softmax回归的表达能力可能不足以捕捉到数据中的更复杂模式。相比之下,前馈神经网络具有更强大的非线性建模能力,可以通过多个隐藏层和非线性激活函数来学习到更复杂的特征表示。SVM也可以通过核函数将低维输入映射到高维空间,从而进行非线性分类。
由此得出结论,但需要注意的是,Softmax回归在所有二分类任务上表现都会远远低于前馈神经网络和SVM。对于一些简单的线性可分问题或数据分布较为简单的情况下,Softmax回归可能表现得很好。然而,对于更复杂的问题和数据集,使用更复杂的模型如前馈神经网络和SVM通常能够获得更好的性能。
但是有个疑问前馈神经网络和SVM究竟哪个更好一点?
简而言之,神经网络是个“黑匣子”,优化目标是基于经验风险最小化,易陷入局部最优,训练结果不太稳定,一般需要大样本;
而支持向量机有严格的理论和数学基础,基于结构风险最小化原则, 泛化能力优于前者,算法具有全局最优性, 是针对小样本统计的理论。
就目前我的理论知识,好像想搞明白哪个好哪个坏可能有点难,而且模型好像很难说哪个好哪个坏,可能针对不同的数据集表现也会不一样,害,浅浅插个眼,等之后,对深度学习有了一定程度的了解的时候再回来,看看有没有一个答案吧。
总结
到此为止前馈神经网络结束啦,有了一点搭建神经网络的经验了吧,大概流程如下:
-
定义网络结构:首先需要确定网络的结构,包括输入层、隐藏层和输出层的大小和数量。
-
初始化参数:对于每个神经元,需要初始化权重和偏置值。权重和偏置值通常是随机初始化的,以避免初始状态过于相似导致模型收敛缓慢。
-
定义损失函数:损失函数用来衡量预测值和真实值之间的误差。二分类问题通常使用交叉熵损失函数,回归问题可以使用均方误差损失函数。
-
定义优化器:优化器用于更新模型的参数,使损失函数最小化。常见的优化器包括随机梯度下降 (SGD)、Adam等。
-
训练模型:通过传递数据进行前向传播和反向传播,更新模型的参数。在训练过程中,需要将数据分为训练集、验证集和测试集。
-
模型评价:在训练完成之后,可以通过输入新数据并进行前向传播来得到预测结果。也可以进行可视化等等。
本次实验对前馈神经网络的应用有更为明确的理解,同时针对softmax,svm,CNN的对比,在实验和搜索资料的过程中,也明白了什么模型更适合应用在什么范围内,softmax和CNN的具体的应用区别还没弄明白算是个小小的遗憾吧,等有更多深度学习经验的时候看看能不能再回来解答这个问题吧~
参考文献
torch.nn.Module所有方法总结及其使用举例_torch.nn.module cuda-CSDN博客
torch.nn — PyTorch master documentation
NNDL 实验五 前馈神经网络(3)鸢尾花分类-CSDN博客
神经网络 VS SVM_svm和神经网络的区别-CSDN博客
相关文章:

基于前馈神经网络完成鸢尾花分类
目录 1 小批量梯度下降法 1.0 展开聊一聊~ 1.1 数据分组 1.2 用DataLoader进行封装 1.3 模型构建 1.4 完善Runner类 1.5 模型训练 1.6 模型评价 1.7 模型预测 思考 总结 参考文献 首先基础知识铺垫~ 继续使用第三章中的鸢尾花分类任务,将Softm…...

软考高级系统架构设计师系列之:UML建模、设计模式和软件架构设计章节选择题详解
软考高级系统架构设计师系列之:UML建模、设计模式和软件架构设计章节选择题详解 一、设计模式二、4+1模型三、面向对象的分析模型四、构件五、基于架构的软件设计六、4+1视图七、软件架构风格八、特定领域软件架构九、虚拟机十、架构评估十一、敏感点和权衡点十二、分层结构十…...

成集云 | 电商平台、ERP、WMS集成 | 解决方案
电商平台ERPWMS 方案介绍 电商平台即是一个为企业或个人提供网上交易洽谈的平台。企业电子商务平台是建立在Internet网上进行商务活动的虚拟网络空间和保障商务顺利运营的管理环境;是协调、整合信息流、货物流、资金流有序、关联、高效流动的重要场所。企业、商家…...

吴恩达《机器学习》4-6->4-7:正规方程
一、正规方程基本思想 正规方程是一种通过数学推导来求解线性回归参数的方法,它通过最小化代价函数来找到最优参数。 代价函数 J(θ) 用于度量模型预测值与实际值之间的误差,通常采用均方误差。 二、步骤 准备数据集,包括特征矩阵 X 和目标…...

VO、DTO
DTO DTO(Data Transfer Object) 数据传输对象【前后端交互】 也就是后端开发过程中,用来接收前端传过来的参数,一般会创建一个Java对应的DTO类(UserDTO等等) 因为前端一般传来的是Json格式的数据…...

RK3566上运行yolov5模型进行图像识别
一、简介 本文记录了依靠RK官网的文档,一步步搭建环境到最终在rk3566上把yolov5 模型跑起来。最终实现的效果如下: 在rk3566 板端运行如下app: ./rknn_yolov5_demo model/RK356X/yolov5s-640-640.rknn model/bus.jpg其中yolov5s-640-640.r…...

汽车标定技术(一):XCP概述
目录 1.汽车标定概述 2.XCP协议由来及版本介绍 3.XCP技术通览 3.1 XCP上下机通信模型 3.2 XCP指令集 3.2.1 XCP帧结构定义 3.2.2 标准指令集 3.2.3 标定指令集 3.2.4 页切换指令集 3.2.5 数据采集指令集 3.2.6 刷写指令集 3.3 ECU描述文件(A2L)概述 3.3.1 标定上位…...

短视频的运营方法
尊敬的用户们,你们好!今天我将为大家带来一篇关于短视频运营的专业文章。在当今互联网时代,短视频已经成为了一个重要的流量入口,掌握正确的运营方法对于企业的发展至关重要。接下来,我将通过以下几个方面为大家详细介…...
GitLab CI/CD 持续集成/部署 SpringBoot 项目
一、GitLab CI/CD 介绍 GitLab CI/CD(Continuous Integration/Continuous Deployment)是 GitLab 提供的一种持续集成和持续部署的解决方案。它可以自动化软件的构建、测试和部署过程,以便开发者更快地、更频繁地发布可靠的产品。 整体过程如…...

第二证券:政策效应逐步显现 A股修复行情有望持续演绎
上星期,A股商场延续企稳反弹的态势,上证指数震荡上涨0.43%;沪深两市日均成交额回升至8700亿元左右;北向资金近一个月初次转为周净买入5.57亿元。 安排观点一起认为,在稳增加、稳预期相关政策持续发力,上市…...

sql逻辑优化
1.分页 通常使用每页条数及第一页作为参数 开发接口 GetMapping("/querySystemList") public List<SystemAduit> querySystemList(RequestParam("keyword") String keyword,RequestParam(name "offset", defaultValue "0") i…...
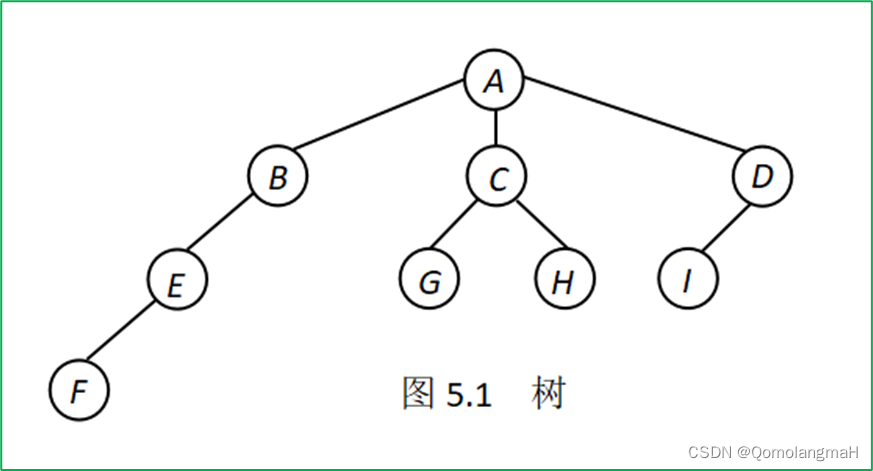
【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
文章目录 5.1 树的基本概念5.1.1 树的定义树有序树、无序树 5.1.2 森林的定义5.1.3 树的术语1. 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(anc…...

2024 Android Framework学习大纲之基础理论篇
2024 Android Framework学习大纲之基础理论篇 受到当前经济影响,互联网越来越不景气了,因此Android App开发也是越来越不景气,中小型公司越来越偏向跨平台开发,比如Flutter,这样能节省成本,笔者也曾经是一名6年多工作经…...

【深度学习】Yolov8 区域计数
git:https://github.com/ultralytics/ultralytics/blob/main/examples/YOLOv8-Region-Counter/readme.md 很长时间没有做yolov的项目了,最近一看yolov8有一个区域计数的功能,不得不说很实用啊。 b站:https://www.bilibili.com/vid…...
Windows 系统服务器部署jar包时,推荐使用winsw,将jar包注册成服务,并设置开机启动。
一、其他方式不推荐的原因 1、Spring Boot生成的jar包,可以直接用java -jar运行,但是前提是需要登录用户,而且注销用户后会退出程序,所以不可用。 2、使用计划任务,写一个bat处理文件,里面写java -jar运行…...

npm 包管理
1. 命令 // 查看是否登录 npm who am i // 登录:输入用户名、密码、邮箱、一次性登录密码(邮箱接收) npm login // 创建 npm init // 快速创建 npm init -y // 发包 npm publish // 发包(开源) npm publish --access …...
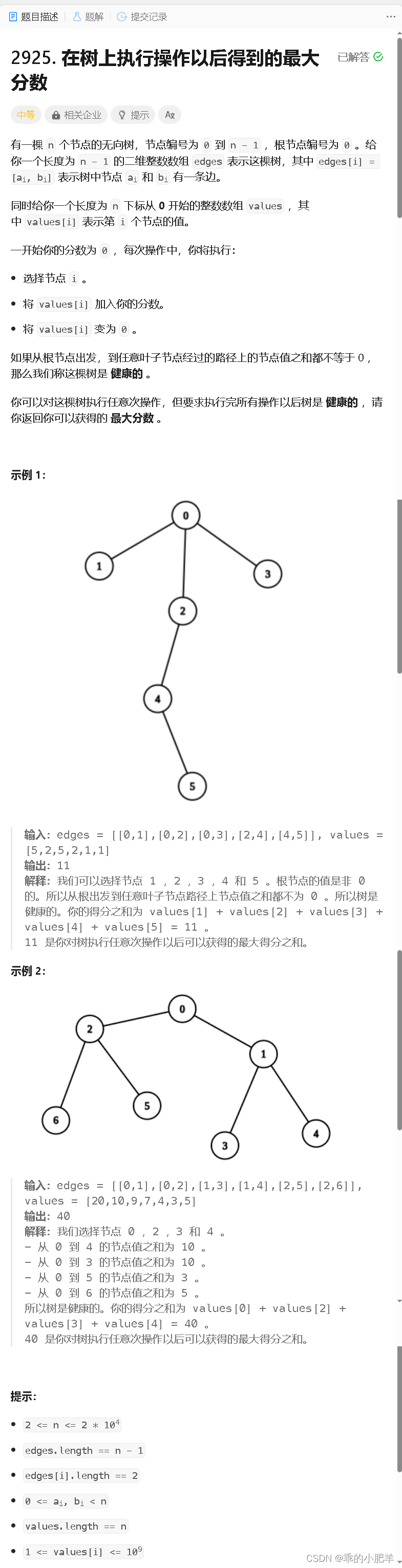
力扣370周赛 -- 第三题(树形DP)
该题的方法,也有点背包的意思,如果一些不懂的朋友,可以从背包的角度去理解该树形DP 问题 题解主要在注释里 //该题是背包问题树形dp问题的结合版,在树上解决背包问题 //背包问题就是选或不选当前物品 //本题求的是最大分数 //先转…...

GPT学习笔记
百度的文心一言 阿里的通义千问 通过GPT能力,提升用户体验和产品力 GPT的出现是AI的iPhone时刻。2007年1月9日,第一代iPhone发布,开启移动互联网时代。新一轮的产业革命。 GPT模型发展时间线: Copilot - 副驾驶 应用…...
Apex的addError()显示的消息中实现换行
直接用‘<br/>’是无效的,因为addError默认不转义HTML符号,如果需要转义,应该将第二个参数escape设置为false。不过即使设置了也只对classic页面生效,lightning页面还是无法转义。 官方文档: 参考资料…...

STM32中微秒延时的实现方式
STM32中微秒延时的实现方式 0.前言一、裸机实现方式二、FreeRTOS实现方式三、定时器实现(通用)4、总结 0.前言 最近在STM32驱动移植过程中需要用到微秒延时来实现一些外设的时序,由于网上找到的驱动方法良莠不齐,笔者在实现时序过…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
