合并分支--将自己的分支合并到master分支
在版本控制系统(例如Git)中,将自己的分支合并到`master`(或者主分支)通常需要以下步骤:
### 1. 切换到主分支
首先,确保你的本地仓库当前处于主分支。你可以使用以下命令切换到主分支:
git checkout master### 2. 拉取最新的代码
在合并分支之前,确保你的主分支是最新的。执行以下命令拉取远程主分支的最新代码:
git pull origin master
### 3. 合并分支
合并分支到主分支,使用以下命令:
git merge your-branch-name在这里,`your-branch-name`是你要合并的分支的名称。如果没有冲突,合并将会成功。
### 4. 解决冲突(如果有的话)
如果在合并的过程中发生了冲突,Git 会暂停合并过程,标记哪些文件有冲突。你需要手动解决这些冲突,然后使用以下命令继续合并:
git add conflicted-file1 conflicted-file2 # 将解决冲突的文件标记为已解决
git merge --continue # 继续合并过程### 5. 提交合并的更改
当合并完成并且冲突已解决,使用以下命令提交合并的更改:
git commit -m "Merge your-branch-name into master"### 6. 推送到远程仓库
最后,将合并后的主分支推送到远程仓库:
git push origin master以上步骤会将你的分支成功合并到主分支。请确保在执行任何涉及版本控制的操作之前备份你的代码,以防意外情况发生。
相关文章:

合并分支--将自己的分支合并到master分支
在版本控制系统(例如Git)中,将自己的分支合并到master(或者主分支)通常需要以下步骤: ### 1. 切换到主分支 首先,确保你的本地仓库当前处于主分支。你可以使用以下命令切换到主分支࿱…...
)
力扣:153. 寻找旋转排序数组中的最小值(Python3)
题目: 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,2,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]若旋转…...
matlab中实现画函数图像添加坐标轴
大家好,我是带我去滑雪! 主函数matlab代码: function PlotAxisAtOrigin(x,y); if nargin 2 plot(x,y);hold on; elsedisplay( Not 2D Data set !) end; Xget(gca,Xtick); Yget(gca,Ytick); XLget(gca,XtickLabel); YLget(gca,YtickLabel)…...
C语言求解一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
完整代码: /* 一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问 该数是多少?*/ #include<stdio.h>int main(){//num为最终所求那个数int num;//i*i为第一个完全平方数for (int i 10; …...

AtCoder abc148
C题 求GCD D题 顺序遍历 E题 trailing zero只与5的个数有关,因此算一下5/25/125…的倍数 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.py # software : PyCharmimport bisect import copy import sys from itertools import perm…...

k8s、docker 卸载
k8s卸载 k8s 重置 kubeadm reset -f如果kubernets是1.24以上版本,请先单独卸载containerd sudo apt purge containerd.iok8s软件卸载 ubuntu #apt卸载 apt purge kubelet kubeadm kubectlcentos yum erase -y kubelet kubectl kubeadm 删除kubelet相关信息&am…...
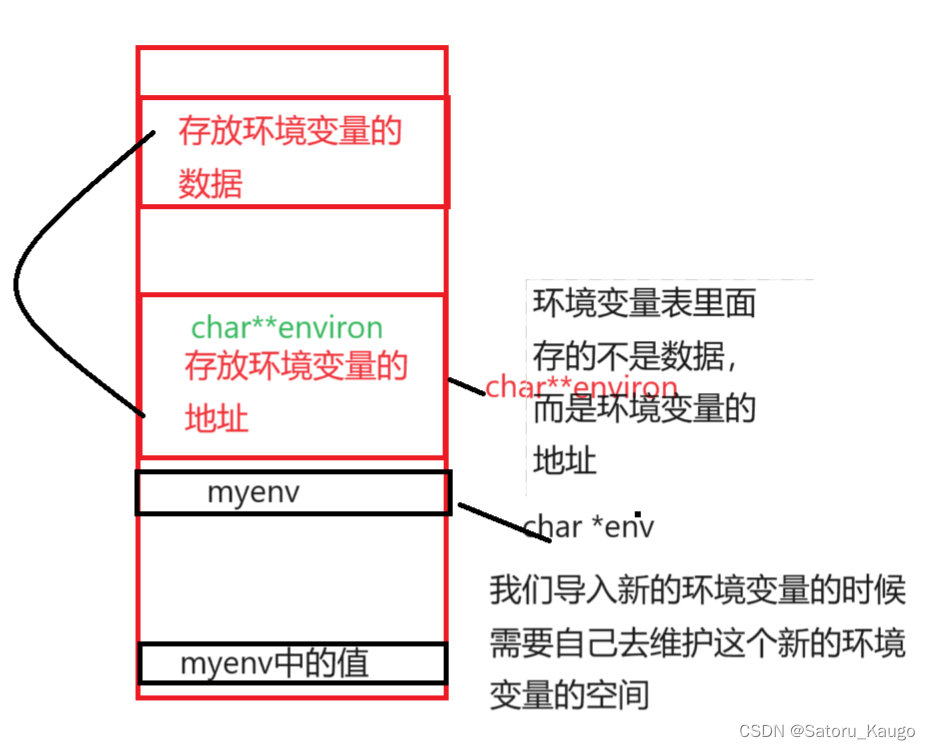
【Linux】Shell命令行的简易实现(C语言实现)内键命令,普通命令
文章目录 0.准备工作1.大体框架 一、获取命令行二、解析命令行三、进程执行1.普通命令2.内建命令 四、完整代码: 0.准备工作 1.大体框架 #include <stdio.h> #include <stdlib.h> #include <string.h> #include <assert.h> #include <u…...
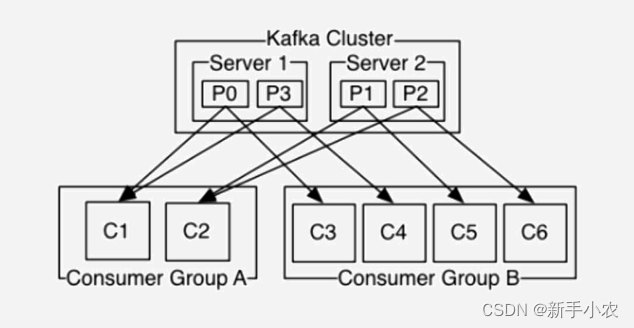
Kafka -- 架构、分区、副本
1、Kafka的架构: 1、producer:消息的生产者 2、consumer:消息的消费者 3、broker:kafka集群的服务者,一个broker就是一个节点,主要是负责处理消息的读、写的请求和存储消息。在kafka cluster中包含很多的br…...

CSS特效001:鼠标放div上,实现旋转、放大、移动等效果
GPT能够很好的应用到我们的代码开发中,能够提高开发速度。你可以利用其代码,做出一定的更改,然后实现效能。 css实战中,经常会看到这样的场景,鼠标放到一个图片或者一个div块状时候,会出现旋转、放大、移动…...

gin 快速入门手册
文章目录 安装URL和路由分组2. 带参数的url3. 获取路由分组的参数 获取参数1. 获取get参数2. 获取post参数3. get、post混合 JSON 、 ProtoBuf渲染1. 输出json和protobuf2. PureJSON 表单验证1. 表单的基本验证 中间件和next函数1. 无中间件启动2. 使用中间件3. 自定义组件 设置…...
Window下安装 Mongodb,并实现单点事务
在window操作系统下安装Mongodb,并让单点mongodb支持事务,mongodb5以上时才支持事务,所以必须时mongodb5及以上版本才支持。 1、下载mongodb安装文件 (1) 下载mongodb msi 安装文件 地址:mongocommunity &…...

【通信原理】第三章 随机过程——例题
一、随机过程 1. 数学特征 ① 随机信号(三角函数表达式) ② 随机信号(求和表达式) 2. 功率谱密度 ① 相位确定,求功率谱密度 ② 已知相位分布,求功率谱密度 ③ 信号为两信号之和,求功率谱密度…...
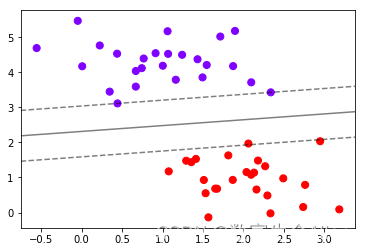
线性【SVM】数学原理和算法实现
一. 数学原理 SVM是一类有监督的分类算法,它的大致思想是:假设样本空间上有两类点,如下图所示,我们希望找到一个划分超平面,将这两类样本分开,我们希望这个间隔能够最大化来使得模型泛化能力最强。 如上图所…...

R语言中的函数26:polyroot多项式求根函数
目录 介绍函数介绍参数含义 示例 介绍 R语言中的base::polyroot()可以用于对多项式求根,求根的多项式可以是复数域上的。 函数介绍 polyroot(z)该函数利用Jenkins-Traub算法对多项式 p ( x ) p(x) p(x)进行求根,其中 p ( x ) z 1 z 2 x ⋯ z n x…...

2023年辽宁省数学建模竞赛A题铁路车站的安全标线
2023年辽宁省数学建模竞赛 A题 铁路车站的安全标线 原题再现: 在火车站或地铁站台上,离站台边缘 1 米左右的地方都画有一条黄线(或白线),这是为什么呢? 这条线称为安全线(业内称之为安全标线),人们在候车时必须站在安全线以…...

半导体工厂将应用哪些制造创新技术?
半导体工厂是高科技产业的结晶,汇聚了世界上最新的技术。 在半导体的原料硅晶片上绘制设计图纸,不产生误差,准确切割并包装,然后用芯片生产出我们使用的电脑、智能手机、手表等各种电子产品。绝大多数半导体厂都采用一贯的工艺&a…...
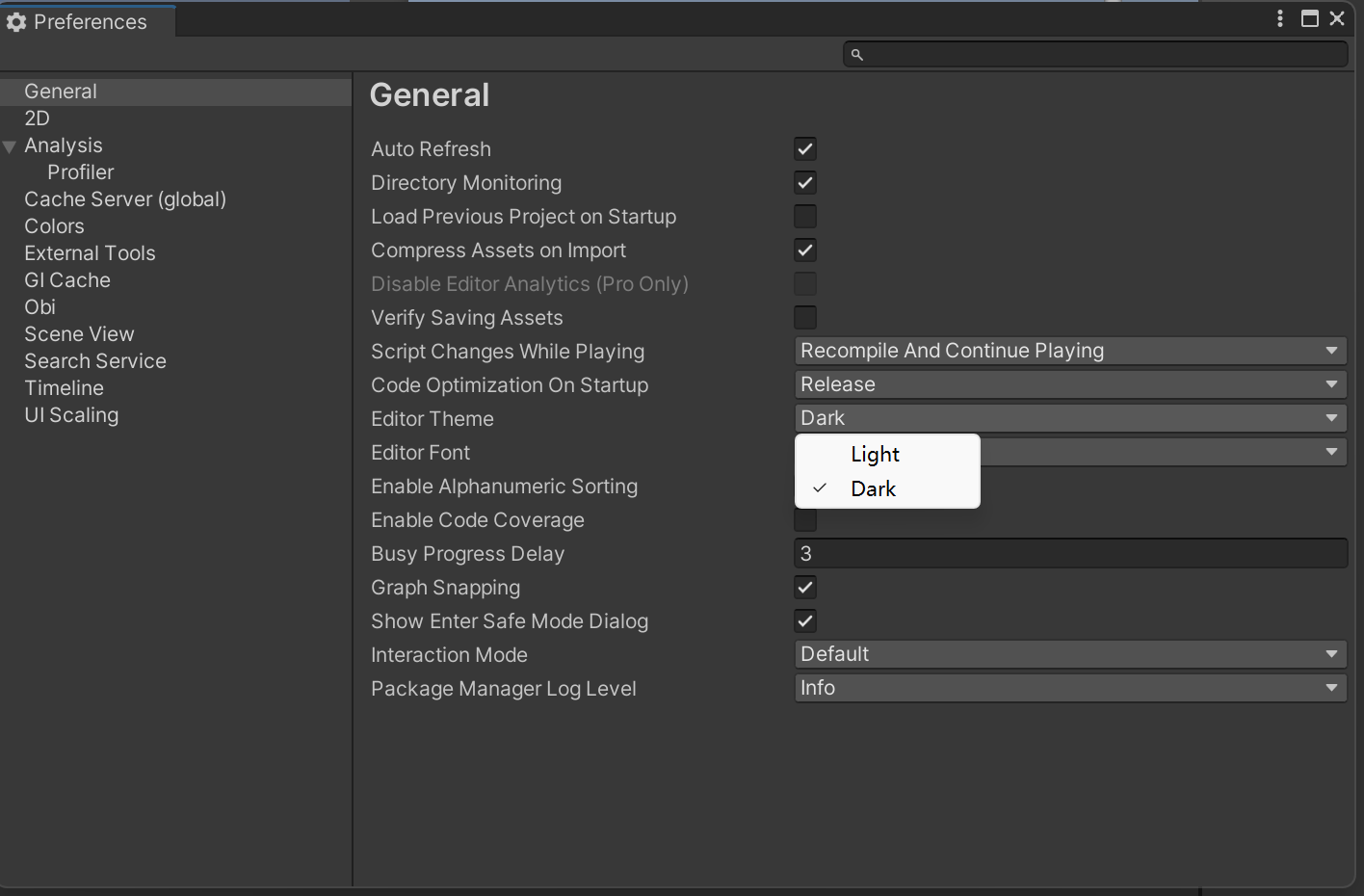
[unity]深色模式/浅色模式
这里用的是Windows版的unity,具体版本号如下: 选项的路径如下:Edit—Preferences—General—Editor Theme 然后就可以选是dark还是light了:...
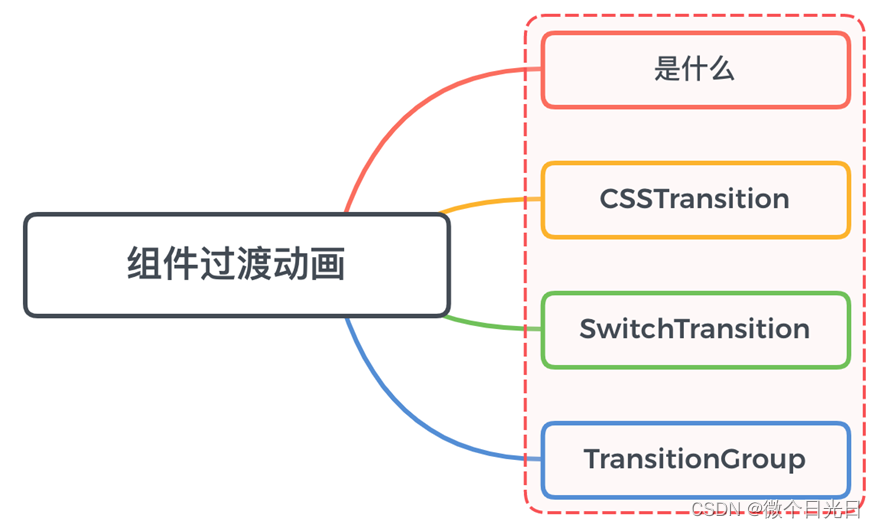
在react中组件间过渡动画如何实现?
一、是什么 在日常开发中,页面切换时的转场动画是比较基础的一个场景 当一个组件在显示与消失过程中存在过渡动画,可以很好的增加用户的体验 在react中实现过渡动画效果会有很多种选择,如react-transition-group,react-motion&…...
解析找不到msvcr100.dll文件的解决方法,4个方法修复msvcr100.dll
msvcr100.dll是Microsoft Visual C 2010运行库的组成部分,一些基于Visual C开发的软件运行时会依赖这个dll文件。出现“找不到msvcr100.dll”的错误提示,往往意味着这个文件在你的计算机系统中丢失或损坏,导致相关程序无法正常运行。以下是找…...

达梦主备部署
达梦主备部署 一.概括1)环境软件下载2)集群规划 二.安装1)安装前2)安装数据库 三.主备机器部署1)初始化数据库(1)主库配置(2)备库配置 2)脱机备份(1)主服务器…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
