算法通关村第八关|白银|二叉树的深度和高度问题【持续更新】
1.最大深度问题(后序遍历)
只需要一直递归,维护一个最大值。每一层只要有一个子节点,这个最大值就可以增加。
public int maxDepth(TreeNode root) {if (root == null) {return 0;}int leftHeight = maxDepth(root.left);int rightHeight = maxDepth(root.right);// 这里要+1,不要漏掉root节点return Math.max(leftHeight, rightHeight) + 1;
}
2.最大深度问题(层次遍历)
遍历出多少层,那么最大深度就是多少。
public int maxDepth(TreeNode root) {if (root == null) {return 0;}Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);int ans = 0;while (!queue.isEmpty()) {int size = queue.size();while (size > 0) {TreeNode node = queue.poll();if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}size--;}ans++;}return ans;
}
3.判断高度平衡二叉树
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。
二叉树的高度:从该节点到叶子节点的节点数。
public Solution {public boolean isBalanced(TreeNode root) {return height(root) >= 0;}public int height(TreeNode root) {if (root == null) {return 0;}int leftHeight = height(root.left);int rightHeight = height(root.right);if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {return -1;} else {return Math.max(leftHeight, rightHeight) + 1;}}
}
4.最小深度(递归)
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
是要有叶子节点才可以算最小深度的,所以当一个节点的一个子树为空,一个不为空的时候,要从不为空的子树继续算深度,不能直接返回结果。
public int minDepth(TreeNode root) {if (root == null) {return 0;}if (root.left == null && root.right == null) {return 1;}// 定义一个min_depth,比较left和right的大小(如果不为空的话)int min_depth = Integer.MAX_VALUE;if (root.left != null) {min_depth = Math.min(minDepth(root.left), min_depth);}if (root.right != null) {min_depth = Math.min(minDepth(root.right), min_depth);}return min_depth + 1;
}
5.最小深度(层次遍历)
找到第一个叶子节点即可。
public int minDepth(TreeNode root) {if (root == null) {return 0;}int minDepth = 0;LinkedList<TreeNode> queue = new LinkedList<TreeNode>();queue.add(root);while (queue.size() > 0) {int size = queue.size();minDepth++;for (int i = 0; i < size; i++) {TreeNode node = queue.poll();// 先判断是不是叶子节点,是就直接返回值if (node.left == null && node.right == null) {return minDepth;}if (node.left != null) {queue.add(node.left);}if (node.right != null) {queue.add(node.right);}}}return 0;
}
6.N叉树的最大深度
N叉树的定义:
class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
}
N叉树的最大深度(递归)
用一个增强 for 循环遍历每个子树即可。
class Solution {public int maxDepth(Node root) {if (root == null) {return 0;} else if (root.children.isEmpty()) {return 1;} else {int max = 0;for (Node item : root.children) {int childrendepth = maxDepth(item);max = Math.max(max, childrendepth);}return max + 1;}}
}
N叉树的最大深度(层次遍历)
【持续更新】。
如果对您有帮助,请点赞关注支持我,谢谢!❤
如有错误或者不足之处,敬请指正!❤
个人主页:星不易 ❤
算法通关村专栏:不易|算法通关村 ❤
相关文章:

算法通关村第八关|白银|二叉树的深度和高度问题【持续更新】
1.最大深度问题(后序遍历) 只需要一直递归,维护一个最大值。每一层只要有一个子节点,这个最大值就可以增加。 public int maxDepth(TreeNode root) {if (root null) {return 0;}int leftHeight maxDepth(root.left);int right…...

cmake 之add_definitions使用误区
需求 需要实现,在cmake中定义宏定义,可以:1) 在code中可以使用;2) 在cmake中可以识别是否已定义 问题 宏定义,cmake有add_definitions函数,直观的实现方法如下。 cmake_minimum…...
Leetcode—515.在每个树行中找最大值【中等】
2023每日刷题(二十三) Leetcode—515.在每个树行中找最大值 DFS实现代码 /*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ /*** Note: The returned arra…...
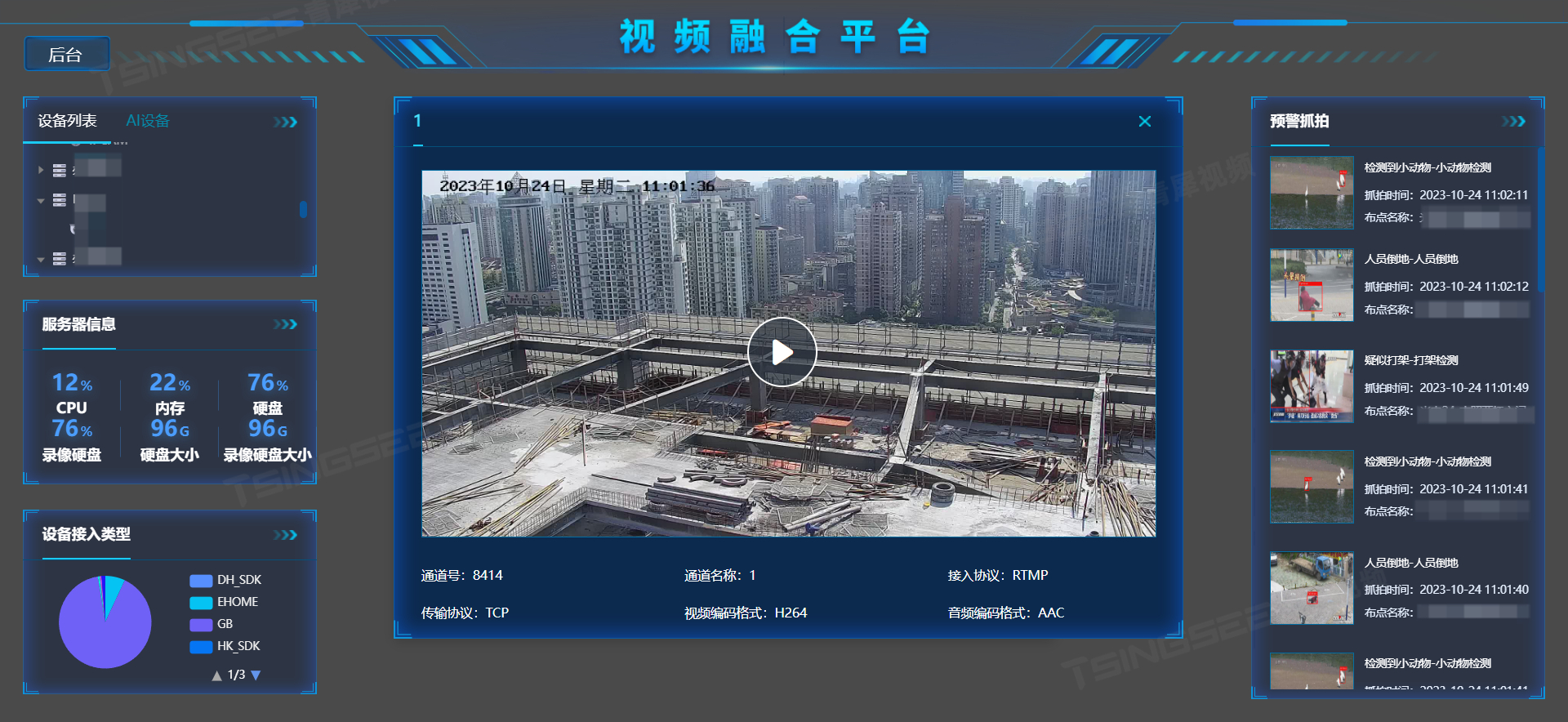
安防监控系统EasyCVR平台设备通道绑定AI算法的功能设计与开发实现
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台可拓展性强、…...

element 弹窗浏览器后退-遮照层还存在问题 以及跟vue keep-alive冲突
问题:element 弹窗浏览器后退-遮照层还存在问题 查询官网可以设置 modal-append-to-body“false” 可以全局设置 ElementUI.Dialog.props.modalAppendToBody.default false 后续 基本到这能解决问题,不过本项目比较特殊,使用了 keep-alive…...

C++(Qt)软件调试---自动注册AeDebug(17)
C(Qt)软件调试—自动注册AeDebug(17) 文章目录 C(Qt)软件调试---自动注册AeDebug(17)1、什么是AeDebug2、使用调试工具3、WinDbg注册到AeDebug4、ProcDump注册到AeDebug5、Dr.MinGW注册到AeDebug6、Visual Studio 注册到AeDebug 1…...

云原生周刊:Gateway API 1.0.0 发布 | 2023.11.6
开源项目推荐 Kueue Kueue 是一套用于作业队列的 API 和控制器。它是作业级管理器,可决定何时允许作业启动(如创建 pod),何时停止作业(如删除活动 pod)。 Reloader 一个 Kubernetes 控制器,…...
Java2 - 数据结构
5 数据类型 5.1 整数类型 在Java中,数据类型用于定义变量或表达式可以存储的数据的类型。Java的数据类型可分为两大类:基本数据类型和引用数据类型。 byte,字节 【1字节】表示范围:-128 ~ 127 即:-2^7 ~ 2^7 -1 sho…...
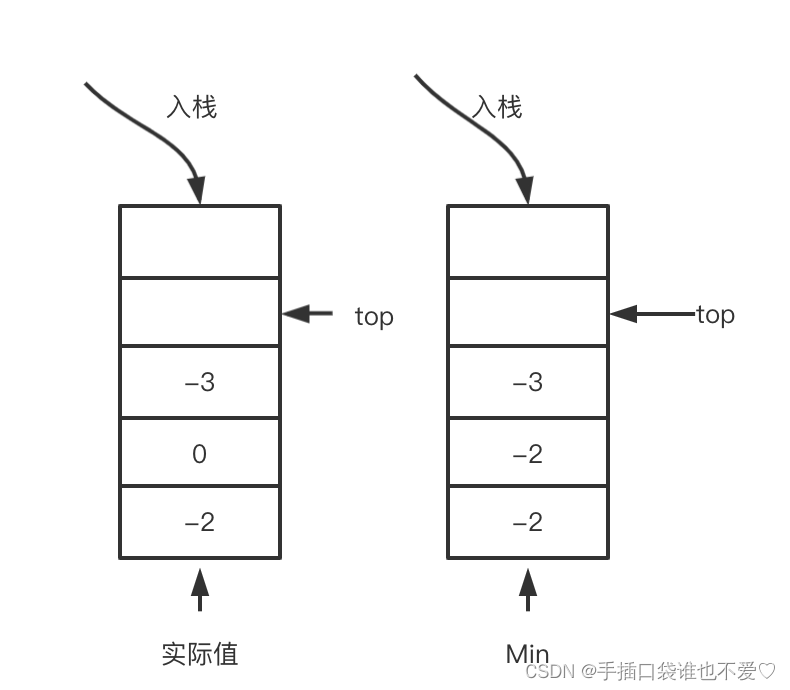
精解括号匹配问题与极致栈设计:揭开最大栈和最小栈的奥秘
目录 括号匹配问题最小栈最大栈 最大栈和最小栈是极致栈的两个重要变种。最大栈用于存储当前匹配的最大值,而最小栈用于存储当前匹配的最小值。 括号匹配问题 这个问题我们来看力扣20题的描述: 给定一个只包括 ‘(’,‘)’,‘{’…...
云存储/视频监控管理平台EasyCVR,使用sqlite数据库出现卡顿该如何优化?
视频集中存储/云存储/视频监控管理平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,实现视频资源的鉴权管理、按需调阅、全网分发、智能分析等。AI智能大数据视频分析EasyCVR平台已经广泛应用在工地、工厂、园区、楼…...

实战!工作中常用的设计模式
文章目录 前言一、策略模式1.1、 业务场景1.2 、策略模式定义1.3、 策略模式使用1.3.1、一个接口,两个方法1.3.2、不同策略的差异化实现1.3.3、使用策略模式 二、责任链模式2.1、业务场景2.2、责任链模式定义2.3、责任链模式使用2.3.1、一个接口或者抽象类2.3.2、每…...

MySQL进阶_1.逻辑架构和SQL执行流程
文章目录 第一节、逻辑架构剖析1.1、服务器处理客户端请求1.2、Connectors1.3、第1层:连接层1.4、第2层:服务层1.5、 第3层:引擎层1.6、 存储层1.7、小结 第二节、SQL执行流程2.1、查询缓存2.2、解析器2.3、优化器2.4、执行器 第三节、数据库…...
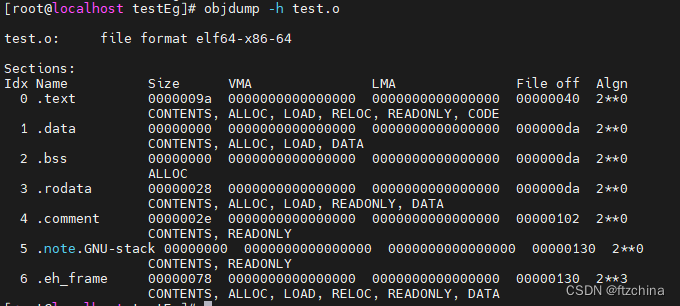
基于GCC的工具objdump实现反汇编
一:objdump介绍 在 Linux中,一切皆文件。 Linux 编程实际上是编写处理各种文件的代码。系统由许多类型的文件组成,但目标文件具有一种特殊的设计,提供了灵活和多样的用途。 目标文件是包含带有附加地址和值的助记符号的路线图。这…...
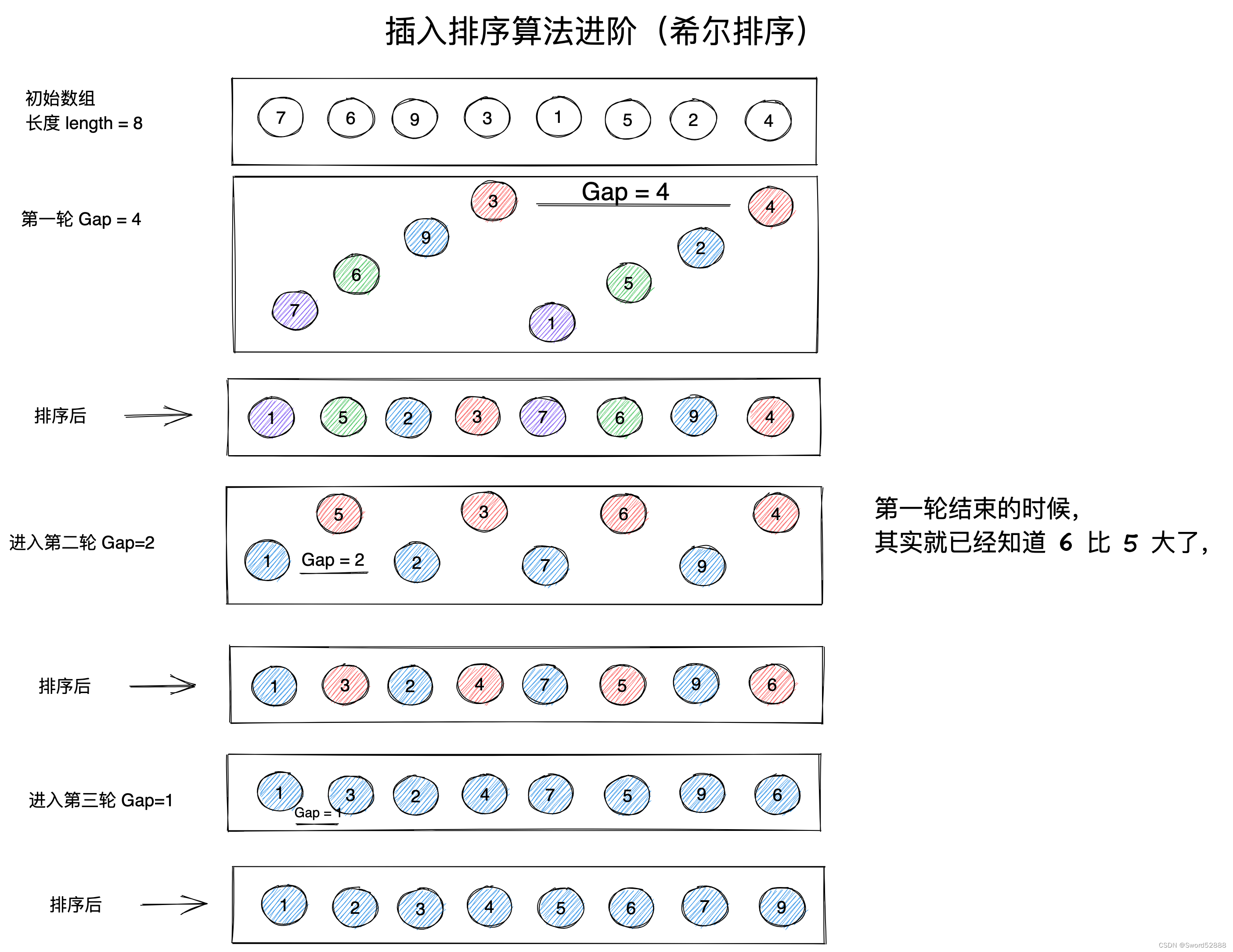
排序算法的空间复杂度和时间复杂度
一、排序算法的时间复杂度和空间复杂度 排序算法 平均时间复杂度 最坏时间复杂度 最好时间复杂度 空间复杂度 稳定性 冒泡排序 O(n) O(n) O(n) O(1) 稳定 直接选择排序 O(n) O(n) O(n) O(1) 不稳定 直接插入排序 O(n) O(n) O(n) O(1) 稳定 快速排序 O(n…...

【电路笔记】-基尔霍夫电路定律
基尔霍夫电路定律 文章目录 基尔霍夫电路定律1、框架和定义2、基尔霍夫电流定律3、基尔霍夫电压定律4、基尔霍夫定律应用5、基尔霍夫定律的局限性6、总结 在本文中,将介绍最基本、最重要的电路定律之一。 这些法律由德国医生古斯塔夫基尔霍夫 (Gustav Kirchoff) 于 …...

从零开始搭建React+TypeScript+webpack开发环境-基于axios的Ajax请求工具
什么是axios axios是一款基于Promise的HTTP客户端,适用于浏览器和Node.js环境。它的特点包括: 支持浏览器和Node.js环境。支持Promise API。支持拦截请求和响应。支持取消请求。自动转换JSON数据。支持CSRF保护。 使用axios可以更方便地发送HTTP请求&…...
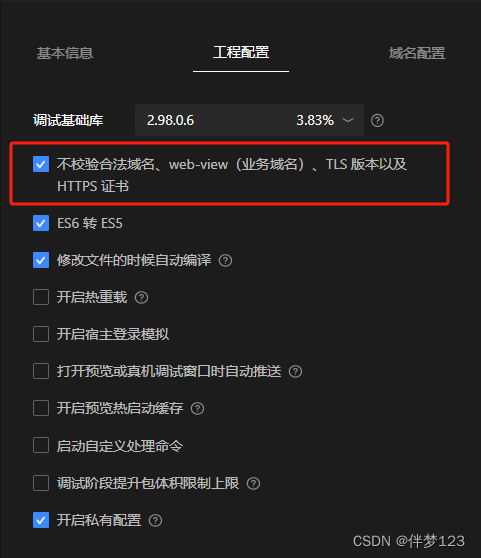
【uniapp小程序下载】调用uni.uploadfile方法在调试工具里是没有问题的,但是线上版本和体验版就调用不成功,真机调试也没问题
把你的下载地址前缀添加到合法域名就解决了 在调试工具里成功了是因为勾选了下面这项 下面是我的下载并打开函数 methods: {// 下载downloadFileFn(data) {if (this.detailsObj.currentUserBuy) {uni.downloadFile({// data是路径url: https:// data,success(res) {//保存到本…...

chatGLM中GLM设计思路
GLM是结合了MLM和CLM的一种预训练方式,其中G为general;在GLM中,它不在以某个token为粒度,而是一个span(多个token),这些span之间使用自编码方式,而在span内部的token使用自回归的方式…...

卡牌游戏类型定制开发微信卡牌小程序游戏
卡牌类型的游戏开发具有一些独特的特点和挑战,以下是一些主要的特点: 卡牌设计和平衡:卡牌游戏的核心是卡牌设计和平衡。开发团队需要设计各种卡牌,确保它们在游戏中相互平衡,以便提供有趣的游戏体验。卡牌的特性、效…...

web —— css(1)
Web —— css基础 1. CSS样式表2. CSS的三种引入方式3. CSS 语法4. CSS 选择器4.1 元素选择器4.2 类选择器4.3 ID选择器4.4 属性选择器4.5 后代选择器4.6 子元素选择器4.7 伪类选择器4.8 分组选择器 5. 颜色和字体6. 显示方式display7. 盒子模型7.1 盒子模型 - 外边距塌陷7.2 盒…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
