当前位置： 首页 > news >正文

恒源云之oss上传数据、云台下载数据

news 2026/2/9 6:38:14

目录

    • 一、本地cmd上传数据
    • 二、使用云平台下载数据

一、本地cmd上传数据

  • 需要下载恒源云客户端oss
  • 需要先将数据（代码、数据集）压缩成zip文件。
  1. 本地cmd打开oss，测试是否安成功
oss

在这里插入图片描述

  1. 输入oss命令，并正确输入账号密码
oss login

在这里插入图片描述

  1. 在个人数据中创建文件夹
oss mkdir oss://datasets

在这里插入图片描述
4. 将本地电脑的 “/文件地址/个人数据.zip” 上传至平台个人数据中的 datasets 文件夹下

oss cp /文件地址/个人数据.zip oss://datasets/
  1. 查看上传的数据
oss ls -s -d oss://datasets/

在这里插入图片描述

二、使用云平台下载数据

  • 需要先在恒源云上创建一个实例
  • （根据镜像（深度学习框架、cuda版本、python版本）买一个合适的云算力服务器（显卡））
  • 打开实例的juypter lub，进入终端Terminal
    在这里插入图片描述
  1. 与本地登录类似：输入oss命令，并正确输入账号密码
oss login

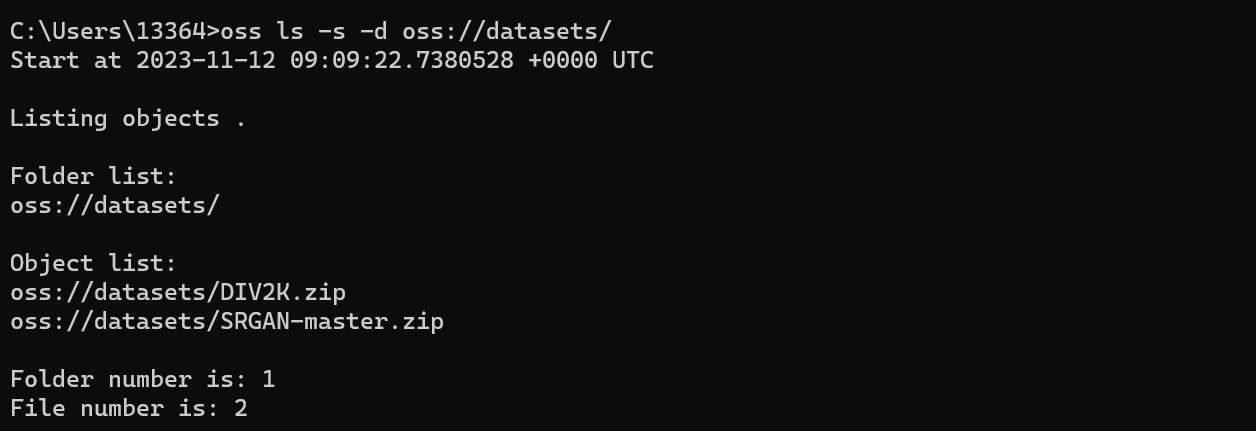
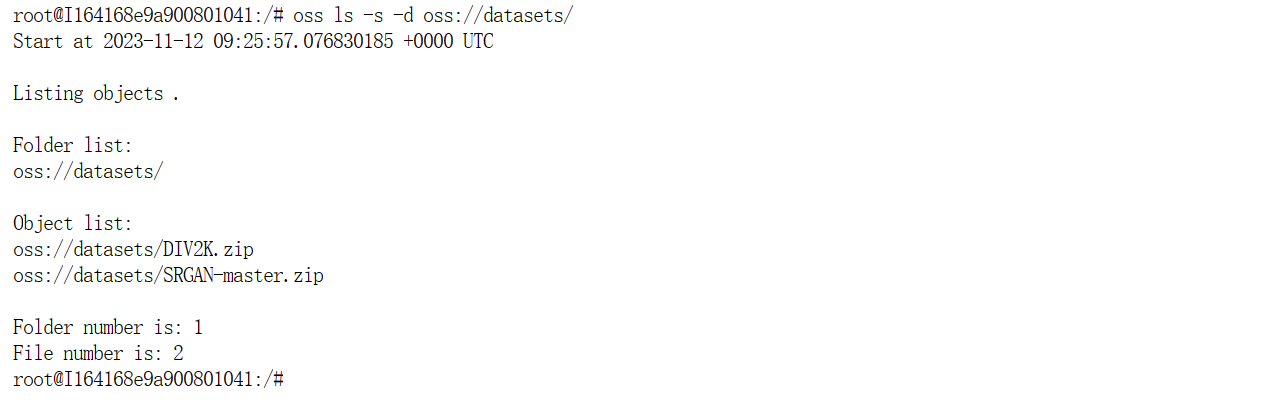
在这里插入图片描述
2. 查看个人数据中的datasets目录

oss ls -s -d oss://datasets/

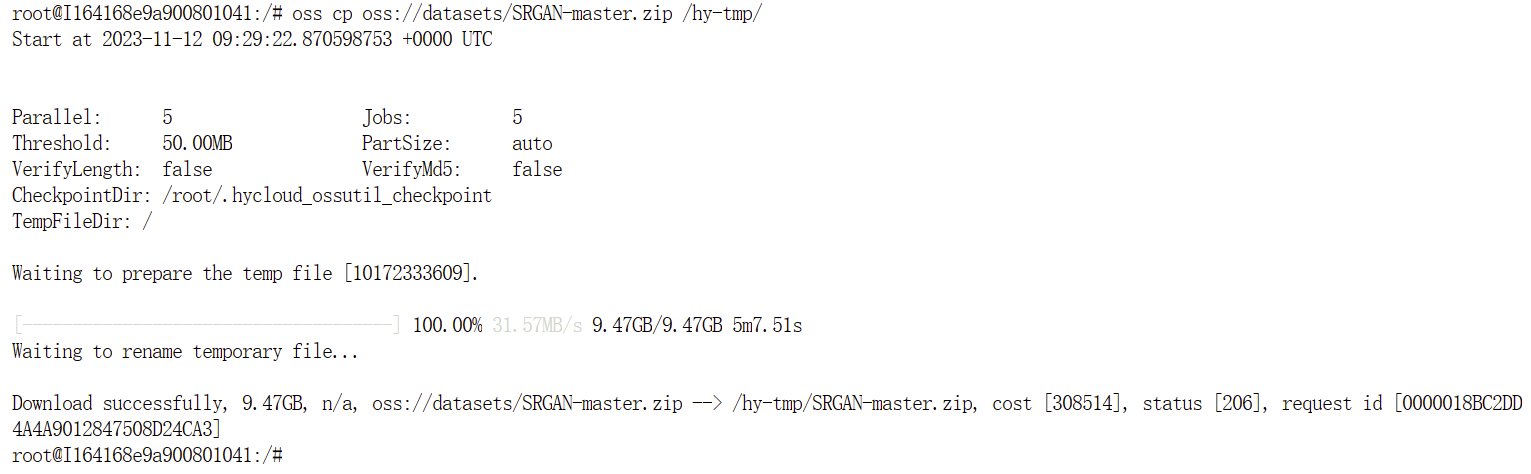
在这里插入图片描述

  1. 下载个人数据到/hy-tmp/目录下
oss cp oss://datasets/个人数据.zip /hy-tmp/

在这里插入图片描述

  1. 查看已下载到/hy-tmp/目录中的数据
ls /hy-tmp/

在这里插入图片描述
5. 进入/hy-tmp/，解压对应文件（程序文件、数据集）

  • 如果文件较小直接使用unzip进行解压缩
unzip 目标文件.zip
  • 如果文件较大（>4GB）使用7z解压
7za x 目标文件.zip
  1. 进如对应的文件路径，运行自己的程序
cd 文件目录

相关文章：

恒源云之oss上传数据、云台下载数据

目录 一、本地cmd上传数据二、使用云平台下载数据 一、本地cmd上传数据 需要下载恒源云客户端oss需要先将数据（代码、数据集）压缩成zip文件。 本地cmd打开oss，测试是否安成功 oss输入oss命令，并正确输入账号密码 oss login在个人…...

编程日记 2023/11/12 19:18:19

大数据-之LibrA数据库系统告警处理（ALM-12039 GaussDB主备数据不同步）

告警解释 GaussDB主备数据不同步，系统每10秒检查一次主备数据同步状态，如果连续6次查不到同步状态，或者同步状态异常，产生告警。 当主备数据同步状态正常，告警恢复。 告警属性 告警ID 告警级别 可自动清除 12039…...

编程日记 2023/11/12 19:17:18

【左程云算法全讲6】链表相关

系列综述： 💞目的：本系列是个人整理为了秋招面试的，整理期间苛求每个知识点，平衡理解简易度与深入程度。 🥰来源：材料主要源于左程云算法课程进行的，每个知识点的修正和深入主要参考…...

编程日记 2023/11/12 19:16:17

从HDFS到对象存储，抛弃Hadoop，数据湖才能重获新生？

Hadoop与数据湖的关系 1、Hadoop时代的落幕2、Databricks和Snowflake做对了什么3、Hadoop与对象存储（OSD）4、Databricks与Snowflake为什么选择对象存储5、对象存储面临的挑战 1、Hadoop时代的落幕 十几年前，Hadoop是解决大规模数据分析的“白…...

编程日记 2023/11/12 19:15:16

灰度与二值化

人工智能的学习之路非常漫长，不少人因为学习路线不对或者学习内容不够专业而举步难行。不过别担心，我为大家整理了一份600多G的学习资源，基本上涵盖了人工智能学习的所有内容。点击下方链接,0元进群领取学习资源,让你的学习之路更加顺畅!记得…...

编程日记 2023/11/12 19:13:14

No183.精选前端面试题，享受每天的挑战和学习

🤍 前端开发工程师（主业）、技术博主（副业）、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...

编程日记 2023/11/12 19:12:13

[C国演义] 第十八章

第十八章 最长斐波那契子序列的长度最长等差数列等差序列划分II - 子序列 最长斐波那契子序列的长度 力扣链接 子序列 ⇒ dp[i] — — 以 arr[i] 结尾的所有子序列中, 斐波那契子序列的最长长度子序列 ⇒ 状态转移方程 — — 根据最后一个位置的组成来划分 初始化 — — 根…...

编程日记 2023/11/12 19:11:12

发送失败的RocktMQ消息，你遇到过吗？

背景 需要通过flink同时向测试和线上的RocketMQ中写入数据 现象 在程序中分别创建了两个MqProducer，设置了不同的nameServerAddr，分别调用不同的producer向不同环境发消息，返回发送成功，但是在线上MQ中却查不到数据&#xff0…...

编程日记 2023/11/12 19:09:10

Unity中全局光照GI的总结

文章目录 前言一、在编写Shader时，有一些隐蔽的Bug不会直接报错，我们需要编译一下让它显示出来，方便修改我们选择我们的Shader，点击编译并且展示编译后的Shader后的内容，隐蔽的Bug就会暴露出来了。 二、我们大概回顾一…...

编程日记 2023/11/12 19:08:09

毫米波雷达技术在自动驾驶中的关键作用：安全、精准、无可替代

自动驾驶技术正以前所未有的速度不断演进，而其中的关键之一就是毫米波雷达技术。作为自动驾驶系统中的核心感知器件之一，毫米波雷达在保障车辆安全、实现精准定位和应对复杂环境中发挥着不可替代的作用。本文将深入探讨毫米波雷达技术在自动驾驶中的关键…...

编程日记 2023/11/12 19:07:08

Jetson平台180度鱼眼相机畸变校正调试记录

1.需求说明 由于使用180度GMSL鱼眼相机，畸变很大； 如需算法使用，必须进行畸变校正 2. 硬件说明 相机： 森云 SG2-AR0233-5300-GMSL2-190H 主板： Jetson NX 3. opencv畸变矫正处理 3.1 获取内参系数 现在森云相机可以直接读取内部flash获取内参系数 3.2 畸变处理 …...

编程日记 2023/11/12 19:06:07

axios请求的问题

本来不想记录，但是实在没有办法，因为总是会出现post请求，后台接收不到数据的情况,还是记录一下如何的解决的比较好。 但是我使用export const addPsiPurOrder data > request.post(/psi/psiPurOrder/add, data); 下面是封装的代码。后台接…...

编程日记 2023/11/12 19:05:06

【pandas刷题系列】Leetcode Problem: [595. 大的国家]

Problem: 595. 大的国家 文章目录 思路解题方法复杂度Code 思路 筛选出对应的数据，然后将不需要的列去除 解题方法 筛选出对应的数据，然后将不需要的列去除 复杂度 时间复杂度: O ( n ) O(n) O(n) 空间复杂度: O ( n ) O(n) O(n) Code import pandas a…...

编程日记 2023/11/12 19:04:05

【打卡】牛客网：BM46 最小的K个数

资料： 1. 排序 sort(name.begin(),name.end()); //升序 sort(name.rbegin(),name.rend()); //降序 【C】vector数组排序_vector排序_比奇堡咻飞兜的博客-CSDN博客 2. 把v2的部分值赋给v1 v1.assign(v2.begin(), v2.end()); // 用新元素替换vector 中的元素。…...

编程日记 2023/11/12 19:03:04

Android各类View触摸监听器失效

在XML布局中出现重叠的View&#xff0c;位置靠后定义的View会覆盖住位置靠前的View&#xff1b;即靠后的View会拦截触碰事件导致靠前的View无法收到触碰事件&#xff0c;无法触发监听器。 //例.<?xml version"1.0" encoding"utf-8"?> <android…...

编程日记 2023/11/12 19:02:02

未整理的知识链接

【scala】下划线用法总结 【scala】下划线用法总结_scala 下划线-CSDN博客 Spark Sql Row 的解析 Spark Sql Row 的解析 - 简书 spark dataframe foreach spark dataframe foreach_mob64ca12f0cf8f的技术博客_51CTO博客 spark- Dataframe基本操作-查询 https://blog.csdn.n…...

编程日记 2023/11/12 19:01:02

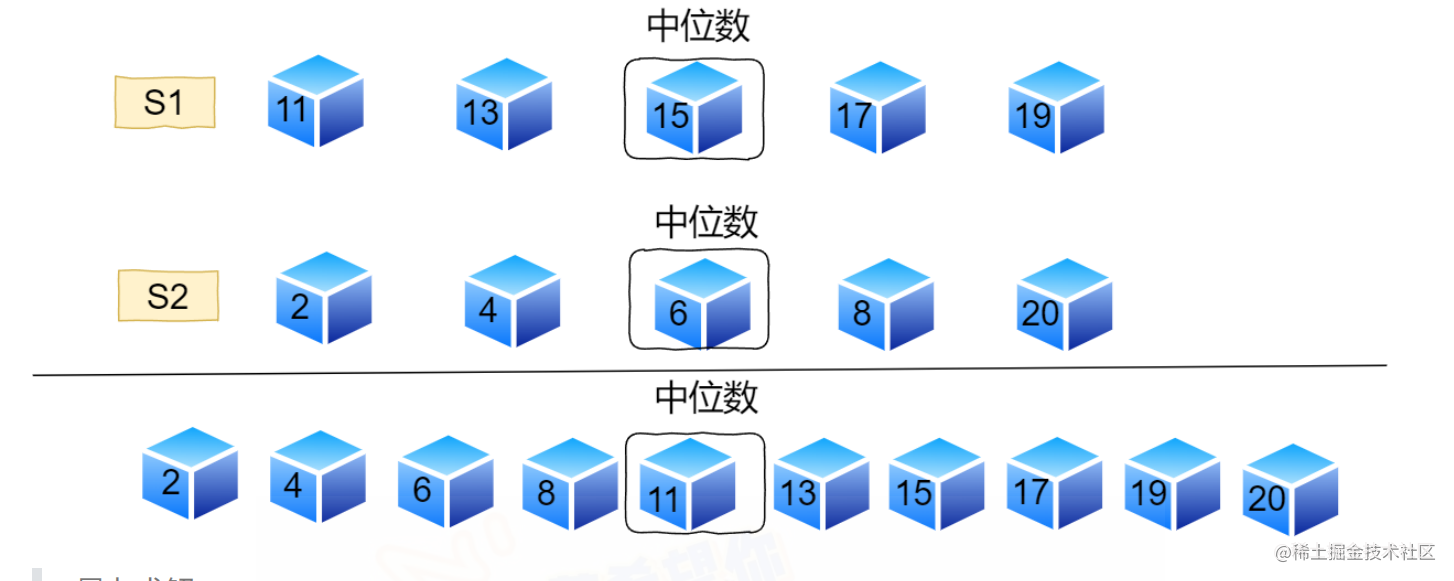
【2011年数据结构真题】

41题 41题解答&#xff1a; &#xff08;1&#xff09;图 G 的邻接矩阵 A 如下所示&#xff1a; 由题意得&#xff0c;A为上三角矩阵&#xff0c;在上三角矩阵A[6][6]中&#xff0c;第1行至第5行主对角线上方的元素个数分别为5, 4, 3, 2, 1 用 “ 平移” 的思想&#xff0c;…...

编程日记 2023/11/12 18:58:59

【科研绘图】MacOS上的LaTeX公式插入工具——LaTeXiT

在Mac上经常用OmniGraffle绘图&#xff0c;但是有个致命缺点是没办法插入LaTeX公式&#xff0c;很头疼。之前有尝试用Pages文稿插入公式&#xff0c;但是调字体和颜色很麻烦。并且&#xff0c;PPT中的公式插入感觉也不太好看。 偶然机会了解到了LaTeXiT这个工具&#xff0c;可…...

编程日记 2023/11/12 18:57:58

仓库自动化中的RFID技术的应用浅谈

仓库自动化与RFID技术的结合代表着现代供应链管理的一个重要革新。这两者的协同作用能够显著提升仓储效率、降低成本、增强库存管理、提高货物跟踪的准确性&#xff0c;并且使仓库操作更加智能化。 仓库自动化是一种通过应用自动化技术和系统来管理和优化仓库操作的方法。这种…...

编程日记 2023/11/12 18:55:57

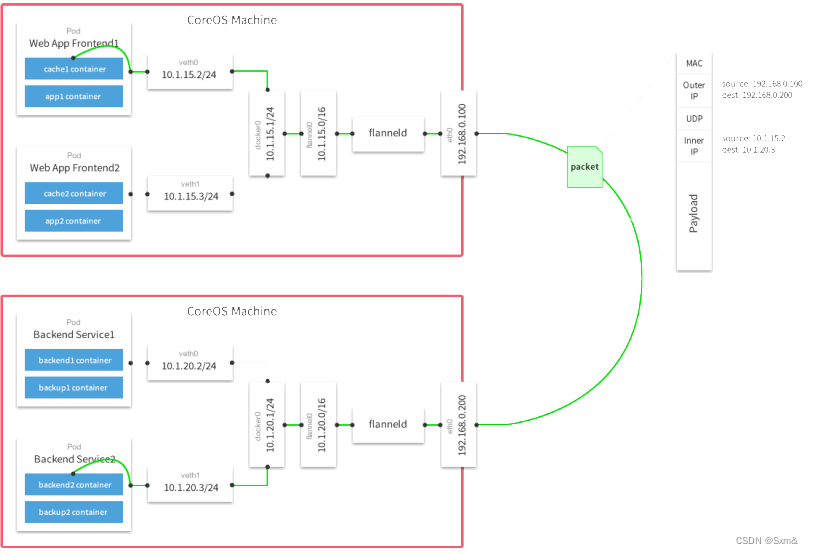
容器网络-Underlay和Overlay

一、主机网络 前面讲了容器内部网络&#xff0c;但是容器最终是要部署在主机上&#xff0c;跨主机间的网络访问又是怎么样的&#xff0c;跨主机网络主要有两种方案。 二、 Underlay 使用现有底层网络&#xff0c;为每一个容器配置可路由的网络IP。也就是说容器网络和主机网络…...

编程日记 2023/11/12 18:54:55

Java 8 Stream API 入门到实践详解

一、告别 for 循环&#xff01; 传统痛点&#xff1a; Java 8 之前&#xff0c;集合操作离不开冗长的 for 循环和匿名类。例如&#xff0c;过滤列表中的偶数&#xff1a; List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

编程新知 2026/1/12 10:41:22

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践

一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架&#xff0c;支持"一次开发&#xff0c;多端部署"&#xff0c;可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务&#xff0c;为旅游应用带来&#xf…...

编程新知 2026/2/5 20:33:43

2.Vue编写一个app

1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

编程新知 2026/1/31 6:04:01

Java多线程实现之Callable接口深度解析

Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

编程新知 2026/1/25 6:36:06

【论文笔记】若干矿井粉尘检测算法概述

总的来说&#xff0c;传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度&#xff0c;通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

编程新知 2025/10/14 10:52:24

反射获取方法和属性

Java反射获取方法 在Java中&#xff0c;反射&#xff08;Reflection&#xff09;是一种强大的机制&#xff0c;允许程序在运行时访问和操作类的内部属性和方法。通过反射&#xff0c;可以动态地创建对象、调用方法、改变属性值&#xff0c;这在很多Java框架中如Spring和Hiberna…...

编程新知 2025/11/9 2:57:17

JVM暂停（Stop-The-World，STW）的原因分类及对应排查方案

JVM暂停（Stop-The-World，STW）的完整原因分类及对应排查方案，结合JVM运行机制和常见故障场景整理而成： 一、GC相关暂停​​ 1. ​​安全点（Safepoint）阻塞​​ ​​现象​​：JVM暂停但无GC日志，日志显示No GCs detected。​​原因​​：JVM等待所有线程进入安全点（如…...

编程新知 2026/2/7 11:25:15

Xen Server服务器释放磁盘空间

disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

编程新知 2025/11/19 6:04:18

用机器学习破解新能源领域的“弃风”难题

音乐发烧友深有体会&#xff0c;玩音乐的本质就是玩电网。火电声音偏暖&#xff0c;水电偏冷&#xff0c;风电偏空旷。至于太阳能发的电&#xff0c;则略显朦胧和单薄。 不知你是否有感觉&#xff0c;近两年家里的音响声音越来越冷&#xff0c;听起来越来越单薄&#xff1f; —…...

编程新知 2026/2/7 22:13:48

让回归模型不再被异常值“带跑偏“，MSE和Cauchy损失函数在噪声数据环境下的实战对比

在机器学习的回归分析中&#xff0c;损失函数的选择对模型性能具有决定性影响。均方误差&#xff08;MSE&#xff09;作为经典的损失函数&#xff0c;在处理干净数据时表现优异&#xff0c;但在面对包含异常值的噪声数据时&#xff0c;其对大误差的二次惩罚机制往往导致模型参数…...

编程新知 2026/1/28 2:18:46