【Leetcode 剑指Offer】第 5 天 查找算法(中等)
查找算法
- 剑指 Offer 04. 二维数组中的查找
- 剑指 Offer 11. 旋转数组的最小数字
- 剑指 Offer 50. 第一个只出现一次的字符
- Python字典基础
- 哈希表(python中是dict())
- 有序哈希表
第一个中等,后两个简单题。
剑指 Offer 04. 二维数组中的查找
题:在一个 n * m 的二维数组中,每一行都按照从左到右 非递减 的顺序排序,每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
这题看到有**暴力解法【时间复杂度O(MN)】**,
有二分法【矩阵 matrix\textit{matrix}matrix 中每一行的元素都是升序排列的,因此我们可以对每一行都使用一次二分查找,判断 target\textit{target}target 是否在该行中,从而判断 target\textit{target}target 是否出现】,
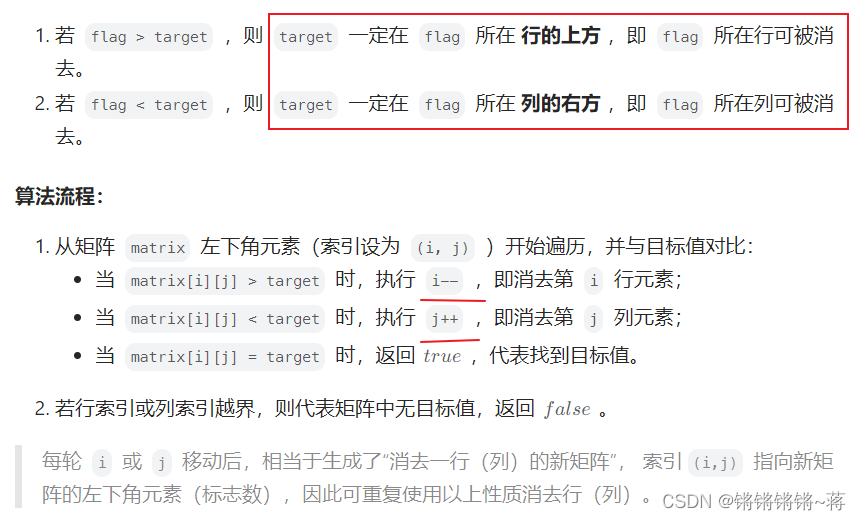
最巧妙好懂的是下面这种,以左下角数字作为标志,最多查找M+N次。**
class Solution:def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:i,j=len(matrix) - 1,0while i>=0 and j<len(matrix[0]):if matrix[i][j]>target:i-=1elif matrix[i][j]<target:j+=1else: return Truereturn False复杂度分析: 时间复杂度 O(M+N) :其中,N和 M分别为矩阵行数和列数,此算法最多循环 M+N 次。 空间复杂度
O(1)O(1)O(1) : i, j 指针使用常数大小额外空间。
作者:Krahets
链接:https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/solutions/95306/mian-shi-ti-04-er-wei-shu-zu-zhong-de-cha-zhao-zuo/
来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
剑指 Offer 11. 旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为 1。
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
思路: 从后往前遍历,找到第一个前一个数比自己大的,这个数就是最小的。
class Solution:def minArray(self, numbers: List[int]) -> int:i=len(numbers)-1while(i>0):if numbers[i]>=numbers[i-1]:i-=1else:return numbers[i]return numbers[0]
剑指 Offer 50. 第一个只出现一次的字符
在字符串 s 中找出第一个只出现一次的字符。如果没有,返回一个单空格。 s 只包含小写字母。

复杂度分析:
时间复杂度 O(N) : N 为字符串 s 的长度;需遍历 s 两轮,使用 O(N);HashMap 查找操作的复杂度为 O(1) ;
空间复杂度 O(1): 由于题目指出 s 只包含小写字母,因此最多有 26 个不同字符,HashMap 存储需占用 O(26)=O(1) 的额外空间。
作者:Krahets
链接:https://leetcode.cn/problems/di-yi-ge-zhi-chu-xian-yi-ci-de-zi-fu-lcof/solutions/159489/mian-shi-ti-50-di-yi-ge-zhi-chu-xian-yi-ci-de-zi-3/
来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
Python字典基础
字典的每个键值 key:value 对用冒号 : 分割,每个键值对之间用逗号 , 分割,整个字典包括在花括号 {} 中;
键一般是唯一且不可变【不能是数组】的,如果重复最后的一个键值对会替换前面的,值不需要唯一。
访问某健的值:dict['key'] 添加更新相同方法;
删除操作:
del tinydict['Name'] # 删除键是'Name'的条目
tinydict.clear() # 清空字典所有条目
del tinydict # 删除字典
哈希表(python中是dict())
! Python 代码中的 not c in dic 整体为一个布尔值; c in dic 为判断字典中是否含有键 c 。
class Solution:def firstUniqChar(self, s: str) -> str:dic = {}for c in s:dic[c] = not c in dicfor c in s:if dic[c]: return creturn ' '
有序哈希表
在哈希表的基础上,有序哈希表中的键值对是 按照插入顺序排序 的。基于此,可通过遍历有序哈希表,实现搜索首个 “数量为 1的字符”。
哈希表是 去重 的,即哈希表中键值对数量 ≤\leq≤ 字符串 s 的长度。因此,相比于方法一,方法二减少了第二轮遍历的循环次数。当字符串很长(重复字符很多)时,方法二则效率更高(第二次搜索dic次)。
class Solution:def firstUniqChar(self, s: str) -> str:dic = collections.OrderedDict()for c in s:dic[c] = not c in dicfor k, v in dic.items():if v: return kreturn ' '
作者:Krahets
链接:https://leetcode.cn/problems/di-yi-ge-zhi-chu-xian-yi-ci-de-zi-fu-lcof/solutions/159489/mian-shi-ti-50-di-yi-ge-zhi-chu-xian-yi-ci-de-zi-3/
来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

【Leetcode 剑指Offer】第 5 天 查找算法(中等)
查找算法剑指 Offer 04. 二维数组中的查找剑指 Offer 11. 旋转数组的最小数字剑指 Offer 50. 第一个只出现一次的字符Python字典基础哈希表(python中是dict())有序哈希表第一个中等,后两个简单题。剑指 Offer 04. 二维数组中的查找 题&#…...

薯条投放适合哪些笔记?小红书薯条投放的3种模式
随着小红书平台的种草推广模式兴盛,薯条投放这个词也渐渐进入大众的视野,今天就来给大家讲讲什么是薯条投放,以及薯条投放适合哪些笔记。一、什么是薯条投放?薯条是一款为小红书用户打造的笔记推广工具,用户可选择推广目标&#…...
记录第一个Python练习的过程
题目如下 编写一个名为collatz()的函数,它有一个名为number的参数。如果参数是偶数,那么collatz()就打印出number // 2,并返回该值。如果number是奇数,collatz()就打印并返回3 * number 1。 然后编写一个程序,让用户…...
【Python】3.3实现多线程
程序Program进程Process线程Thread为完成特定任务而用计算机语言编写的一组计算机能识别和执行的指令的集合。程序是指令、数据及其组织形式的描述,一段静态代码,静态对象。计算机中的程序关于某数据集合上的一次执行过程。进程是程序的实体,…...

在linux中使用lftp和sftp下载文件(夹)
一、首先确保你的系统中已经下载了lftp和sftp。 1.安装lftp sudo apt install lftp sudo apt install screen 2.安装sftp 在Linux系统中,一般RedHat系统默认已经安装了openssh-client和openssh-server,即默认已经集成了sftp服务,不需要重…...

Docker简介与用法
文章目录1、Docker简介1.1、Docker能解决什么问题1.2、什么是虚拟机技术1.2.1、虚拟机的缺点1.3、什么是容器1.3.1、容器与虚拟机比较1.4、分析 Docker 容器架构1.4.1、Docker客户端和服务器1.4.2、Docker 镜像(Image)1.4.3、Docker 容器(Container)1.4.4、Docker 仓库(reposit…...

基于海鸥算法改进的DELM分类-附代码
海鸥算法改进的深度极限学习机DELM的分类 文章目录海鸥算法改进的深度极限学习机DELM的分类1.ELM原理2.深度极限学习机(DELM)原理3.海鸥算法4.海鸥算法改进DELM5.实验结果6.参考文献7.Matlab代码1.ELM原理 ELM基础原理请参考:https://blog.c…...

linux基本功系列之mount命令实战
文章目录前言一. mount命令的介绍二. 语法格式及常用选项三. 参考案例3.1 将iso镜像挂载到/mnt上3.2 把某个分区挂载到/sdb1上3.3 用只读的形式把/dev/sdb2挂载到/sdb2上3.4 设置自动挂载总结前言 大家好,又见面了,我是沐风晓月,本文是专栏【…...
力扣Top100题之两数相加(Java解法)
0 题目描述 给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。 请你将两个数相加,并以相同形式返回一个表示和的链表。 你可以假设除了数字 0 之外,这两个数…...
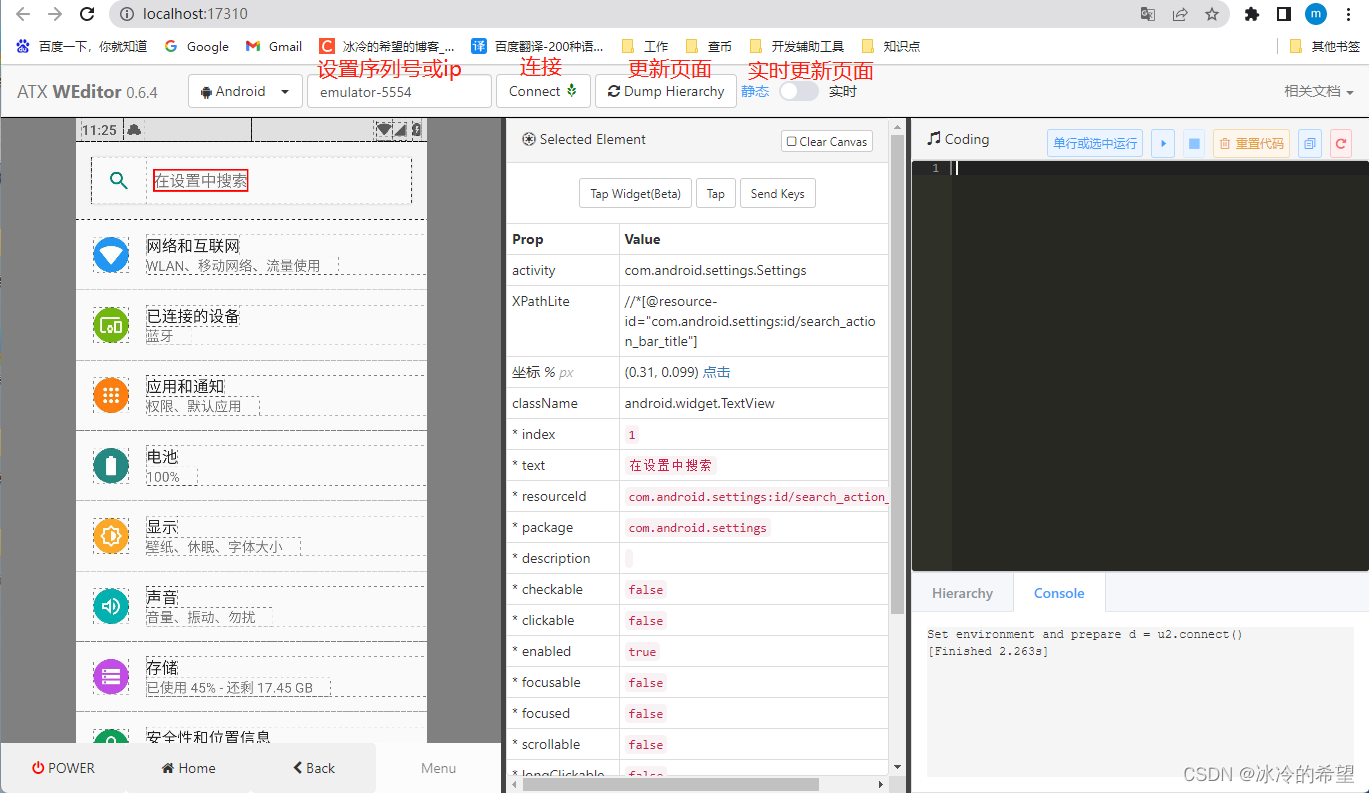
【测试】Python手机自动化测试库uiautomator2和weditor的详细使用
1.说明 我们之前在电脑操作手机进行自动化测试,基本上都是通过Appium的,这个工具确实强大,搭配谷歌官方的UiAutomator基本上可以完成各种测试,但缺点也很明显,配置环境太麻烦了,需要jdk、sdk等,…...

《NFL橄榄球》:旧金山49人·橄榄1号位
旧金山四九人(San Francisco 49ers,又译旧金山淘金者) 是美国全国橄榄球联盟球队。成立于1946年,最初作为全美橄榄球联合会(AAFC)的一员参加比赛,后于1950年与克利夫兰布朗一同加入由美国橄榄球联合会合并而成的NFL。现任主教练为…...
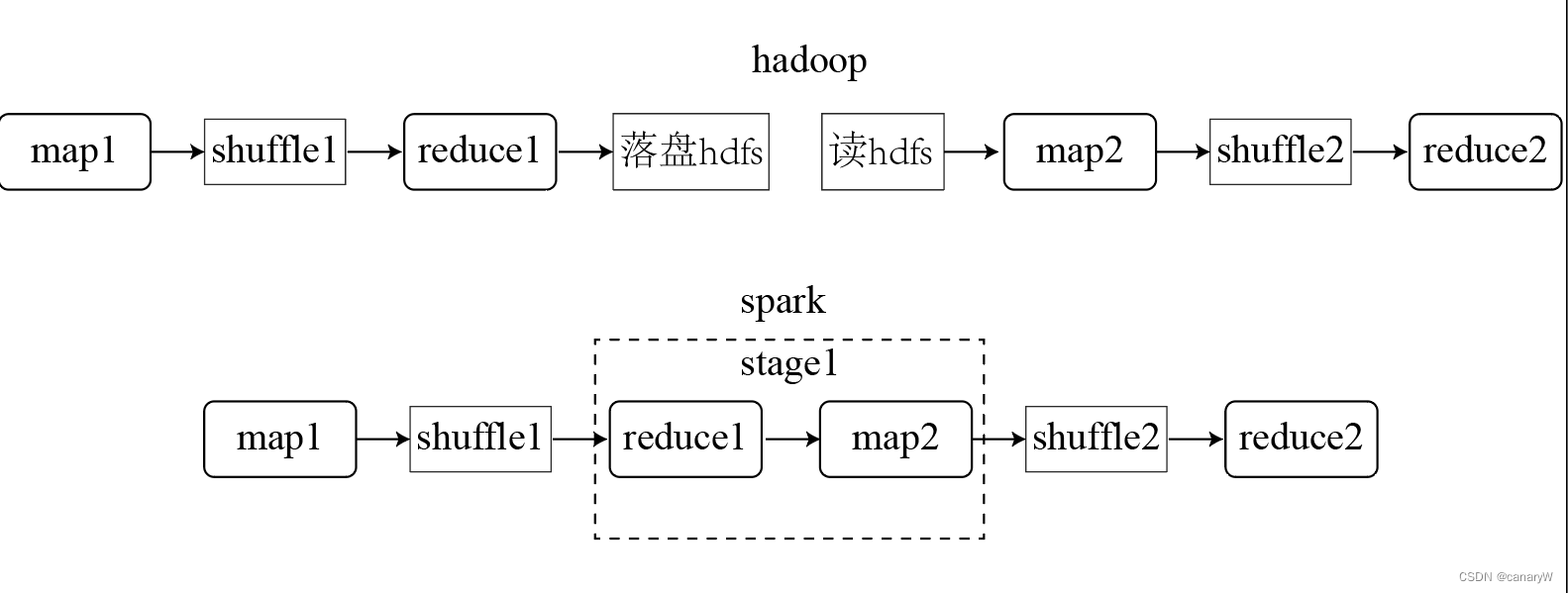
spark为什么比hadoop快
网上一堆人根本对计算框架一知半解就出来糊弄人,常见解答有: spark是基于内存计算,所以快。这跟废话似的,mr计算的时候不也是基于内存? mr shuffle落盘。这也是胡扯, spark shuffle不落盘? 实际…...

跨境人都在用的指纹浏览器到底有什么魔力?三分钟带你了解透彻
什么是指纹浏览器?这是东哥近期收到最多的粉丝私信咨询,指纹两个字大家都很熟悉,指纹浏览器就变得陌生起来。之前东哥也跟大家分享过很多次指纹浏览器的用法,鉴于还是很多人不认识这个好用的工具,东哥今天就来详细给大…...
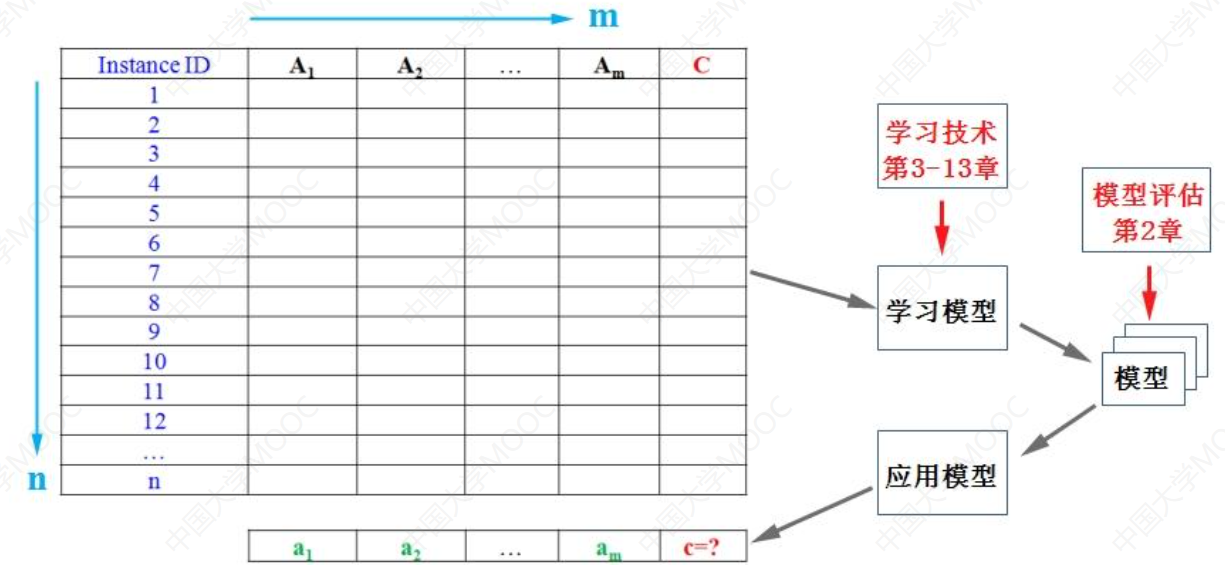
机器学习概述
机器学习是人工智能的核心研究领域之一,其研究动机是为了让计算机系统具有人的学习能力以便实现人工智能。目前被广泛采用的机器学习的定义是“利用经验来改善计算机系统自身的性能”。由于“经验在计算机系统中主要是以数据的形式存在的,因此机器学习需…...
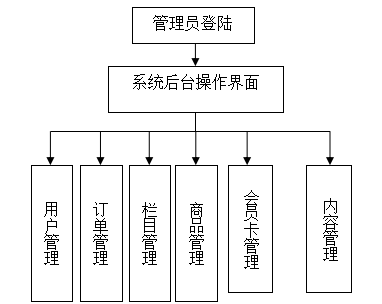
企业网站自动生成系统的设计和实现
技术:Java、JSP等摘要:随着Internet技术的发展,人们的日常生活已经离不开网络。未来社会人们的生活和工作将越来越依赖于数字技术的发展,越来越数字化、网络化、电子化、虚拟化。Internet的发展历程以及目前的应用状况和发展趋势&…...

sikuli+eclipse对于安卓app自动化测试的应用
Sikuli是什么? 下面是来自于官网的介绍:Sikuli is a visual technology to automate and test graphical user interfaces (GUI) using images (screenshots). Sikuli includes Sikuli Script, a visual scripting API for Jython, and Sikuli IDE, an …...
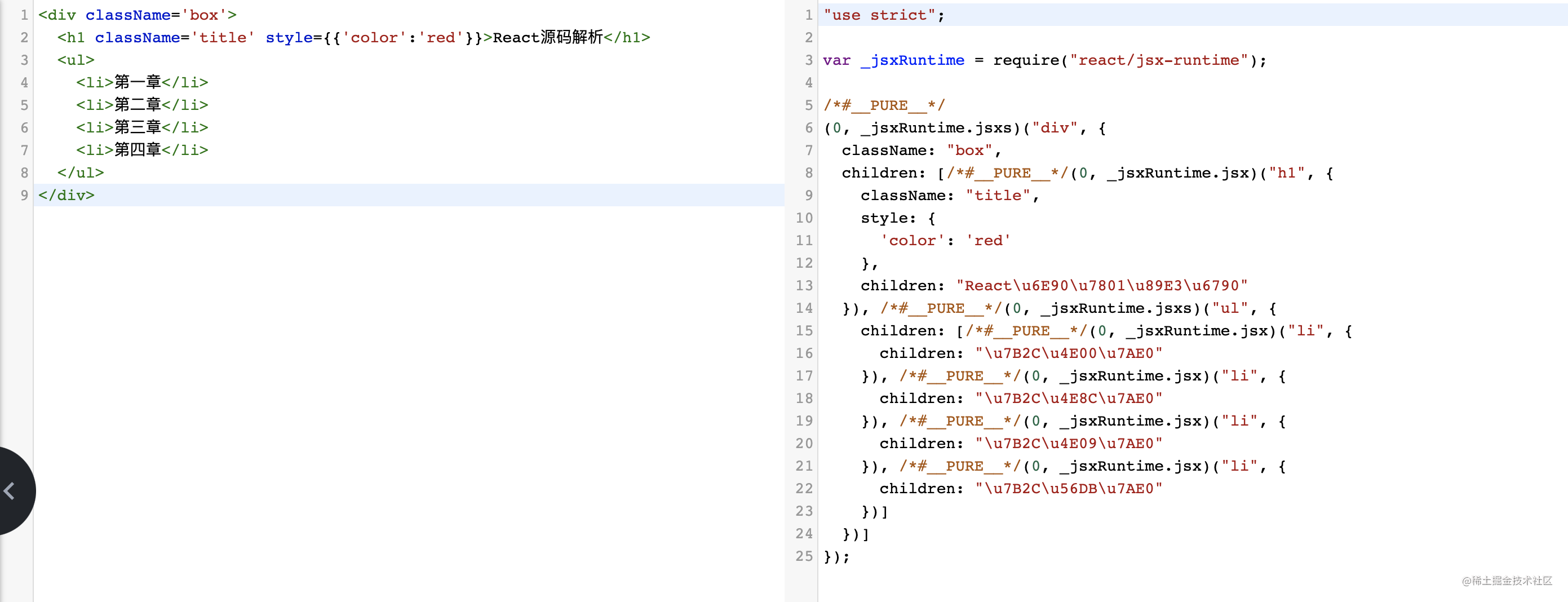
react源码分析:babel如何解析jsx
同作为MVVM框架,React相比于Vue来讲,上手更需要JavaScript功底深厚一些,本系列将阅读React相关源码,从jsx -> VDom -> RDOM等一些列的过程,将会在本系列中一一讲解 工欲善其事,必先利其器 经过多年的…...

搜广推 WideDeep 与 DeepCrossNetwork (DCN) - 记忆+泛化共存
😄 这节来讲讲Wide&Deep与Deep&CrossNetwork (DCN)。从下图可看出WD非常重要,后面衍生出了一堆WD的变体。本节要讲的WD和DCN结构都非常简单,但其设计思想值得学习。 🚀 wide&deep:2016年,谷歌提出。 🚀 Deep&CrossNetwork (DCN):2017年,谷歌和斯坦…...
项目管理工具dhtmlxGantt甘特图入门教程(十四):导出/导入 Excel到 iCal
这篇文章给大家讲解利用dhtmlxgantt导入/导出Excel到iCal的操作方法。 dhtmlxGantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表,可满足应用程序的所有需求,是完善的甘特图图表库 DhtmlxGantt正版试用下载(qun;765665…...
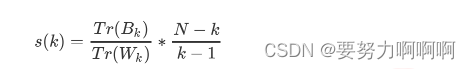
k-means聚类总结
1.概述 聚类算法又叫做‘无监督学习’,其目的是将数据划分成有意义或有用的组(或簇)。 2.KMeans 关键概念:簇与质心 KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上来看是簇是一组一组聚集在一起的…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
