Please No More Sigma(构造矩阵)
Please No More Sigma
给f(n)定义如下:
f(n)=1 n=1,2;
f(n)=f(n-1)+f(n-2) n>2;
给定n,求下式模1e9+7后的值

Input
第一行一个数字T,表示样例数 以下有T行,每行一个数,表示n。 保证T<=100,n<=100000000
Output
输出式子的值。由于直接求值会很大,输出模1e9+7后的结果。
Sample Input
2 1 2
Sample Output
1 4
思路:
写出前几项的形式;
设g(n)为i=n时的和,s(n)为f(n)前n项和,h(n)为i=1到i=n的总和。
可以找到规律:
g(n)=g(n-1)+s(n);
h(n)=h(n-1)+g(n);
然后构造矩阵:

代码:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<unordered_map>
#include<map>
using namespace std;
typedef long long LL;
typedef unsigned long long ull;
#define per(i,a,b) for(int i=a;i<=b;i++)
#define ber(i,a,b) for(int i=a;i>=b;i--)
const int N = 1e5;
const long long mod = 1e9 + 7;
const double eps = 1e-2;
typedef struct data
{
LL m[5][5];
}J;
J Q, E;
J now, ans;
LL f[5];
void into()
{
Q = { 0,1,0,0,0,
1,1,0,0,0,
0,1,1,0,0,
0,0,1,1,0,
0,0,0,1,1,};
E = { 1,0,0,0,0,
0,1,0,0,0,
0,0,1,0,0,
0,0,0,1,0,
0,0,0,0,1};
}
J quickfu(J a, J b)
{
J c;
for (int i = 0; i <= 4; i++)
for (int j = 0; j <= 4; j++)
{
c.m[i][j] = 0;
for (int k = 0; k <= 4; k++)
c.m[i][j] = (c.m[i][j] + a.m[i][k] * b.m[k][j] % mod) % mod;
c.m[i][j] = (c.m[i][j] % mod + mod) % mod;
}
return c;
}
J quick(J a, LL b)
{
J ans = E;
while (b)
{
if (b & 1)
ans = quickfu(ans, a);
b >>= 1;
a = quickfu(a, a);
}
return ans;
}
LL n;
int main()
{
int T;
cin >> T;
into();
while (T--)
{
cin >> n;
if (n == 0)
{
cout << 0 << endl;
continue;
}
else if (n == 1)
{
cout << 1 << endl;
continue;
}
f[0] = 1, f[1] =2 , f[2] = 2, f[3] = 1,f[4]=0;
now = Q;
ans = quick(now, n);
LL an = 0;
for (int i = 0; i <= 4; i++)
an = (an + ans.m[4][i] * f[i] % mod) % mod;
cout << (an % mod + mod) % mod << endl;
}
return 0;
}
相关文章:

Please No More Sigma(构造矩阵)
Please No More Sigma 给f(n)定义如下: f(n)1 n1,2; f(n)f(n-1)f(n-2) n>2; 给定n,求下式模1e97后的值 Input 第一行一个数字T,表示样例数 以下有T行,每行一个数,表示n。 保证T<100,n<100000…...
HTML设置标签栏的图标
添加此图标最简单的方法无需修改内容,只需按以下步骤操作即可: 1.准备一个 ico 格式的图标 2.将该图标命名为 favicon.ico 3.将图标文件置于index.html同级目录即可 为什么我的没有变化? 答曰:ShiftF5强制刷新一下网页就行了...

4.CentOS7安装MySQL5.7
CentOS7安装MySQL5.7 2023-11-13 小柴你能看到嘛 哔哩哔哩视频地址 https://www.bilibili.com/video/BV1jz4y1A7LS/?vd_source9ba3044ce322000939a31117d762b441 一.解压 tar -xvf mysql-5.7.26-linux-glibc2.12-x86_64.tar.gz1.在/usr/local解压 tar -xvf mysql-5.7.44-…...

【华为OD题库-014】告警抑制-Java
题目 告警抑制,是指高优先级告警抑制低优先级告警的规则。高优先级告警产生后,低优先级告警不再产生。请根据原始告警列表和告警抑制关系,给出实际产生的告警列表。不会出现循环抑制的情况。告警不会传递,比如A->B.B->C&…...

高频SQL50题(基础题)-5
文章目录 主要内容一.SQL练习题1.602-好友申请:谁有最多的好友代码如下(示例): 2.585-2016年的投资代码如下(示例): 3.185-部门工资前三高的所有员工代码如下(示例): 4.1667-修复表中的名字代码…...

Spring IoC DI 使⽤
关于 IoC 的含义,推荐看IoC含义介绍(Spring的核心思想) 喜欢 Java 的推荐点一个免费的关注,主页有更多 Java 内容 前言 通过上述的博客我们知道了 IoC 的含义,既然 Spring 是⼀个 IoC(控制反转)…...

Zigbee智能家居方案设计
背景 目前智能家居物联网中最流行的三种通信协议,Zigbee、WiFi以及BLE(蓝牙)。这三种协议各有各的优势和劣势。本方案基于CC2530芯片来设计,CC2530是TI的Zigbee芯片。 网关使用了ESP8266CC2530。 硬件实物 节点板子上带有继电器…...

机器视觉目标检测 - opencv 深度学习 计算机竞赛
文章目录 0 前言2 目标检测概念3 目标分类、定位、检测示例4 传统目标检测5 两类目标检测算法5.1 相关研究5.1.1 选择性搜索5.1.2 OverFeat 5.2 基于区域提名的方法5.2.1 R-CNN5.2.2 SPP-net5.2.3 Fast R-CNN 5.3 端到端的方法YOLOSSD 6 人体检测结果7 最后 0 前言 ǵ…...
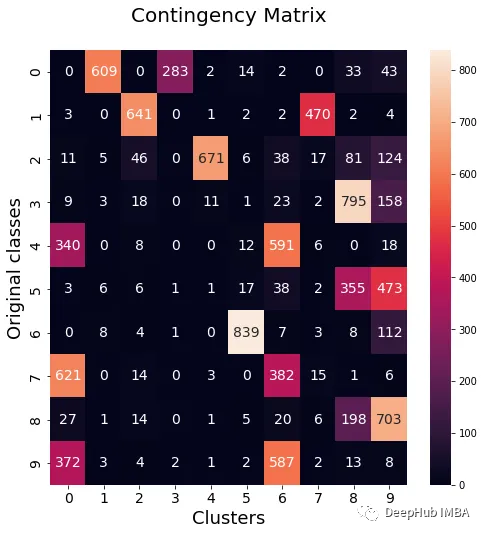
无监督学习的集成方法:相似性矩阵的聚类
在机器学习中,术语Ensemble指的是并行组合多个模型,这个想法是利用群体的智慧,在给出的最终答案上形成更好的共识。 这种类型的方法已经在监督学习领域得到了广泛的研究和应用,特别是在分类问题上,像RandomForest这样…...

16. 机器学习——决策树
机器学习面试题汇总与解析——决策树 本章讲解知识点 什么是决策树决策树原理决策树优缺点决策树的剪枝决策树的改进型本专栏适合于Python已经入门的学生或人士,有一定的编程基础。 本专栏适合于算法工程师、机器学习、图像处理求职的学生或人士。 本专栏针对面试题答案进行了…...

DevOps系列---【jenkinsfile使用sshpass发送到另一台服务器】
1.首先在宿主机安装sshpass 2.把物理机的sshpass复制到容器中 which sshpass cp $(which sshpass) /usr/local/app/ docker cp sshpass 容器id:/usr/local/bin/sshpass 3.在jenkinsfile中添加 #在stages中添加stage stage(部署TEST服务){steps{sh "sshpass -p root1234 sc…...

Docker 和 Kubernetes:技术相同和不同之处
Docker和Kubernetes是当今最流行的容器化技术解决方案。本文将探讨Docker和Kubernetes的技术相似之处和不同之处,以帮助读者更好地理解这两种技术。 Docker和Kubernetes:当今最流行的容器化技术解决方案 在当今的IT领域,Docker和Kubernetes无…...

通信世界扫盲基础二(原理部分)
上次我们刚学习了关于通信4/G的组成和一些通识,今天我们来更深层次了解一些原理以及一些新的基础~ 目录 专业名词 LTE(4G系统) EPC s1 E-UTRAN UE UU X2 eNodeB NR(5G系统) NGC/5GC NG NG-RAN Xn gNodeB N26接口 手机的两种状态 空闲态 连接态 …...

手机厂商参与“百模大战”,vivo发布蓝心大模型
在2023 vivo开发者大会上,vivo发布自研通用大模型矩阵——蓝心大模型,其中包含十亿、百亿、千亿三个参数量级的5款自研大模型,其中,10亿量级模型是主要面向端侧场景打造的专业文本大模型,具备本地化的文本总结、摘要等…...

【微软技术栈】C#.NET 中的泛型
本文内容 定义和使用泛型泛型的利与弊类库和语言支持嵌套类型和泛型 借助泛型,你可以根据要处理的精确数据类型定制方法、类、结构或接口。 例如,不使用允许键和值为任意类型的 Hashtable 类,而使用 Dictionary<TKey,TValue> 泛型类并…...
【毕业论文】基于微信小程序的植物分类实践教学系统的设计与实现
基于微信小程序的植物分类实践教学系统的设计与实现https://download.csdn.net/download/No_Name_Cao_Ni_Mei/88519758 基于微信小程序的植物分类实践教学系统的设计与实现 Design and Implementation of Plant Classification Practical Teaching System based on WeChat Mini…...

[量化投资-学习笔记011]Python+TDengine从零开始搭建量化分析平台-MACD金死叉策略回测
在上一章节 MACD金死叉中结束了如何根据 MACD 金死叉计算交易信号。 目录 脚本说明文档(DevChat 生成)MACD 分析脚本安装依赖库参数配置查询与解析数据计算 MACD 指标判断金叉和死叉计算收益绘制图形运行脚本 本次将根据交易信号,模拟交易。更…...
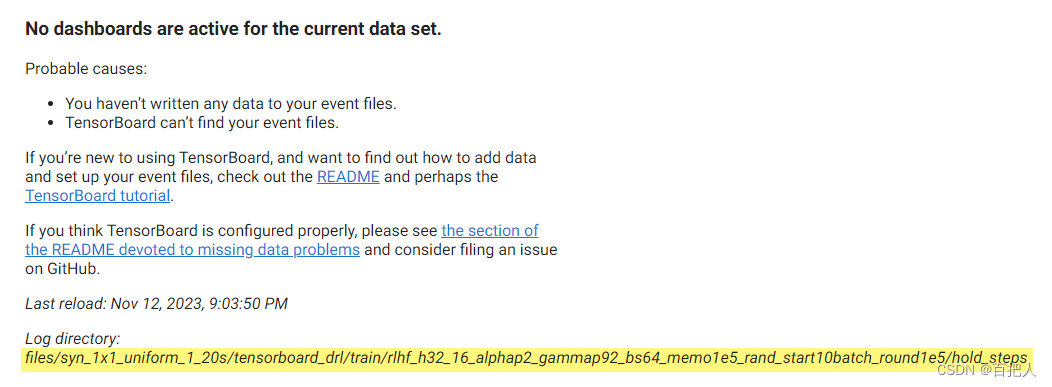
tensorboard报错解决:No dashboards are active for the current data set
版本:tensorboard 2.10.0 问题:文件夹下明明有events文件,但用tensorboard命令却无法显示。 例如: 原因:有可能是文件路径太长了,导致系统无法读取文件。在win系统中规定,目录的绝对路径不得超…...

线性代数本质系列(一)向量,线性组合,线性相关,矩阵
本系列文章将从下面不同角度解析线性代数的本质,本文是本系列第一篇 向量究竟是什么? 向量的线性组合,基与线性相关 矩阵与线性相关 矩阵乘法与线性变换 三维空间中的线性变换 行列式 逆矩阵,列空间,秩与零空间 克莱姆…...

python语法之注释
注释可用于解释Python代码。 注释可用于使代码更易读。 注释可用于在测试代码时阻止执行。 (1)创建注释 注释以#开头,Python会忽略它们: #This is a comment print("Hello, World!") 注释可以放在一行…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...
