数据结构-二叉排序树(建立、查找、修改)
二叉排序树概念
二叉排序树是动态查找表的一种,也是常用的表示方法。
其中,它具有如下性质:
1.若它的左子树非空,则其左子树的所有节点的关键值都小于根节点的关键值。
2.若它的右子树非空,则其右子树的所有节点的关键值都大于根结点的关键值。
3.它的左右子树也分别都是二叉排序树。
PS:对二叉排序树进行中序遍历,得到的序列,总会是一个升序的数列。
二叉排序树的建立
我们使用C语言来建立。
其中我们对二叉排序树的结构体定义如下:
typedef int ElemType;
typedef struct BTNode{ElemType key;struct BTNode *lchild,*rchild;
}BTNode,*BSTree;建立二叉排序树的代码如下:
BSTree InsertBST(BSTree bst,BSTree s) //遍历二叉排序树,找到合适的位置
{if(bst==NULL)bst = s;else{if(s->key < bst->key)bst->lchild = InsertBST(bst->lchild,s);if(s->key > bst->key){bst->rchild = InsertBST(bst->rchild,s);}}return bst;
}BSTree CreateBST() //建立二叉排序树
{BSTree bst,s;int key;bst = NULL;printf("请输入关键字值,输入-1结束.\n");while(1){scanf("%d",&key);if(key!=-1){s = (BSTree)malloc(sizeof(BTNode));s->key = key;s->lchild = NULL;s->rchild = NULL;bst = InsertBST(bst,s);printf("成功.\n");}elsebreak;}return bst;
}
二叉排序树的插入
BSTree InsertBST(BSTree bst,BSTree s) //遍历二叉排序树,找到合适的位置
{if(bst==NULL)bst = s;else{if(s->key < bst->key)bst->lchild = InsertBST(bst->lchild,s);if(s->key > bst->key){bst->rchild = InsertBST(bst->rchild,s);}}return bst;
}BSTree SearchBST(BSTree bst,int key) //查找关键值key的节点,并且返回这个节点
{if(bst == NULL)return NULL;else if(key == bst->key)return bst;else if(key > bst->key)return SearchBST(bst->rchild,key);elsereturn SearchBST(bst->lchild,key);
}BSTree InsertBST_key(BSTree bst,int key) //搜寻一个关键值,如果没有就插入
{BSTree s;s = SearchBST(bst,key);if(s)printf("该节点已经存在.");else{s = (BSTree)malloc(sizeof(BTNode));s->key = key;s->lchild = NULL;s->rchild = NULL;s = InsertBST(bst,s);}return s;
}查找二叉排序树指定节点的双亲
BSTree SearchBST_F(BSTree bst,int key,BSTree *F) //F存储key关键值节点的双亲节点,函数返回key关键值节点.
{if(bst == NULL)return NULL;if(key == bst->key)return bst;else{*F = bst;if(key < bst->key)return SearchBST_F(bst->lchild,key,F);elsereturn SearchBST_F(bst->rchild,key,F);}
}
相关文章:
)
数据结构-二叉排序树(建立、查找、修改)
二叉排序树概念 二叉排序树是动态查找表的一种,也是常用的表示方法。 其中,它具有如下性质: 1.若它的左子树非空,则其左子树的所有节点的关键值都小于根节点的关键值。 2.若它的右子树非空,则其右子树的所有节点的…...

Linux 性能优化之使用 Tuned 配置优化方案
写在前面 考试整理相关笔记博文内容涉及 Linux tuned 调优工具的简单认知调优配置文件的简单说明,自定义调优方案介绍理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意ÿ…...

Day02_《MySQL索引与性能优化》
文章目录 一、SQL执行顺序二、索引简介1、关于索引2、索引的类型Btree 索引Btree 索引 三、Explain简介四、Explain 详解1、id2、select_type3、table4、type5、possible_keys6、key7、key_len8、ref9、rows10、Extra11、小案例 五、索引优化1、单表索引优化2、两表索引优化3、…...
(只需三步)Vmvare tools安装教程,实现与windows互通复制粘贴与文件拖拽
首先确保Ubuntu是联网的,如果连不上网可以参考我的这个联网教程,也很简单 (只需三步)虚拟机上vm的ubuntu不能联上网怎么办-CSDN博客 第一步:卸载之前的tools,确保没有残留 sudo apt-get autoremove open-vm-tools 第…...

Android自定义控件:一款多特效的智能loadingView
先上效果图(如果感兴趣请看后面讲解): 1、登录效果展示 2、关注效果展示 1、【画圆角矩形】 画图首先是onDraw方法(我会把圆代码写上,一步一步剖析): 首先在view中定义个属性:priv…...
C语言之初阶指针
一、指针: 其实按照我的理解,当我们写c语言程序的时候,创建的变量,数组等都要在内存上开辟空间。而每一个内存都有一个唯一的编号,这个编号也被称为地址编号,就相当于,编号地址指针。 二、指针…...
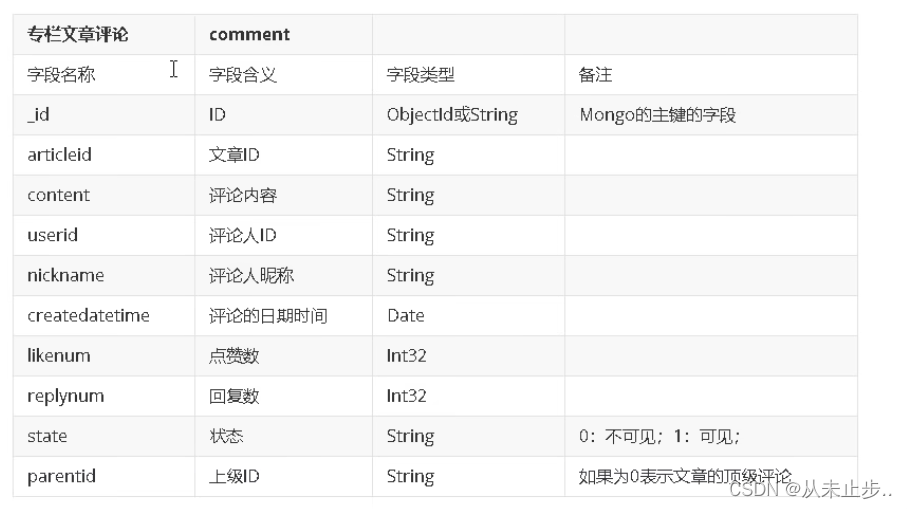
MongoDB基础知识~
引入MongoDB: 在面对高并发,高效率存储和访问,高扩展性和高可用性等的需求下,我们之前所学习过的关系型数据库(MySql,sql server…)显得有点力不从心,而这些需求在我们的生活中也是随处可见的,例如在社交中…...

41. 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 示例 1: 输入:nums [1,2,0] 输出:3示例 2: 输入:nums [3…...
数据结构—数组栈的实现
前言:各位小伙伴们我们前面已经学习了带头双向循环链表,数据结构中还有一些特殊的线性表,如栈和队列,那么我们今天就来实现数组栈。 目录: 一、 栈的概念 二、 栈的实现 三、 代码测试 栈的概念: 栈的概念…...

AI大模型低成本快速定制秘诀:RAG和向量数据库
文章目录 1. 前言2. RAG和向量数据库3. 论坛日程4. 购票方式 1. 前言 当今人工智能领域,最受关注的毋庸置疑是大模型。然而,高昂的训练成本、漫长的训练时间等都成为了制约大多数企业入局大模型的关键瓶颈。 这种背景下,向量数据库凭借其独特…...

Please No More Sigma(构造矩阵)
Please No More Sigma 给f(n)定义如下: f(n)1 n1,2; f(n)f(n-1)f(n-2) n>2; 给定n,求下式模1e97后的值 Input 第一行一个数字T,表示样例数 以下有T行,每行一个数,表示n。 保证T<100,n<100000…...
HTML设置标签栏的图标
添加此图标最简单的方法无需修改内容,只需按以下步骤操作即可: 1.准备一个 ico 格式的图标 2.将该图标命名为 favicon.ico 3.将图标文件置于index.html同级目录即可 为什么我的没有变化? 答曰:ShiftF5强制刷新一下网页就行了...

4.CentOS7安装MySQL5.7
CentOS7安装MySQL5.7 2023-11-13 小柴你能看到嘛 哔哩哔哩视频地址 https://www.bilibili.com/video/BV1jz4y1A7LS/?vd_source9ba3044ce322000939a31117d762b441 一.解压 tar -xvf mysql-5.7.26-linux-glibc2.12-x86_64.tar.gz1.在/usr/local解压 tar -xvf mysql-5.7.44-…...

【华为OD题库-014】告警抑制-Java
题目 告警抑制,是指高优先级告警抑制低优先级告警的规则。高优先级告警产生后,低优先级告警不再产生。请根据原始告警列表和告警抑制关系,给出实际产生的告警列表。不会出现循环抑制的情况。告警不会传递,比如A->B.B->C&…...

高频SQL50题(基础题)-5
文章目录 主要内容一.SQL练习题1.602-好友申请:谁有最多的好友代码如下(示例): 2.585-2016年的投资代码如下(示例): 3.185-部门工资前三高的所有员工代码如下(示例): 4.1667-修复表中的名字代码…...

Spring IoC DI 使⽤
关于 IoC 的含义,推荐看IoC含义介绍(Spring的核心思想) 喜欢 Java 的推荐点一个免费的关注,主页有更多 Java 内容 前言 通过上述的博客我们知道了 IoC 的含义,既然 Spring 是⼀个 IoC(控制反转)…...

Zigbee智能家居方案设计
背景 目前智能家居物联网中最流行的三种通信协议,Zigbee、WiFi以及BLE(蓝牙)。这三种协议各有各的优势和劣势。本方案基于CC2530芯片来设计,CC2530是TI的Zigbee芯片。 网关使用了ESP8266CC2530。 硬件实物 节点板子上带有继电器…...

机器视觉目标检测 - opencv 深度学习 计算机竞赛
文章目录 0 前言2 目标检测概念3 目标分类、定位、检测示例4 传统目标检测5 两类目标检测算法5.1 相关研究5.1.1 选择性搜索5.1.2 OverFeat 5.2 基于区域提名的方法5.2.1 R-CNN5.2.2 SPP-net5.2.3 Fast R-CNN 5.3 端到端的方法YOLOSSD 6 人体检测结果7 最后 0 前言 ǵ…...
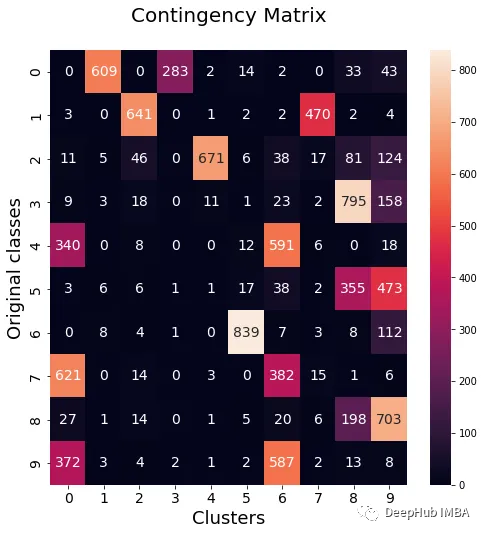
无监督学习的集成方法:相似性矩阵的聚类
在机器学习中,术语Ensemble指的是并行组合多个模型,这个想法是利用群体的智慧,在给出的最终答案上形成更好的共识。 这种类型的方法已经在监督学习领域得到了广泛的研究和应用,特别是在分类问题上,像RandomForest这样…...

16. 机器学习——决策树
机器学习面试题汇总与解析——决策树 本章讲解知识点 什么是决策树决策树原理决策树优缺点决策树的剪枝决策树的改进型本专栏适合于Python已经入门的学生或人士,有一定的编程基础。 本专栏适合于算法工程师、机器学习、图像处理求职的学生或人士。 本专栏针对面试题答案进行了…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
