归并排序(含递归和非递归版)

文章目录
- 引入:
- 实现原理
- 问题引出:
- 递归实现:
- 迭代实现
- 稳定性分析:
- 总结:
引入:
如何将两个有序数组(假设为升序)合并为一个有序数组?
双指针法,如果第一个数组的第一个元素大于第二个数组的元素,就取第二个(即较小的那个放在合并的数组的首位置),然后在比较第一个数组第一个元素与第二个数组的第二个元素,以此类推,终将有一个数组的元素先被访问完,剩下的那个数组的元素一定是大于已经排序后的数组,直接将未排完序的数组的元素添加到我们要合并数组即可。
代码如下
while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}
实现原理
归并排序就是利用上边的思想进行排序,将无序的数组不断折中至最短,并在合并的过程中将两个数组进行合并并排序。其是建立在归并操作上的一种有效的排序方式,采用分治法,将已经排好序的子序列合并,得到完全有序的序列,在归的过程中将待排序的数组分为各个小块,在并的过程中不断使每个小区间变为有序,最终使该数组有序。
过程刨析

问题引出:
能否在原数组进行排序?
- 如果直接进行数据覆盖的话明显不可以,会将未修改的元素覆盖,直接修改了数组元素,这种想法必然是错误的。
- 聪明的同学会想到那么我用交换的形式呢?
看下边这种情况

第二个小数组区间已经排好的序已经被打乱,在后边的排序中,比较时就是先和5比,再和4比,这就违反了我们两个有序数组分别从第一个元素比大小将小的那个放在合并的数组的第一个位置的核心思想。
引出空间复杂度,顺便也说一说他的时间复杂度,我想大家已经有所猜测了,毕竟和二分法沾边的算法。
空间复杂度:
使用归并排序的方法时要开一份同样大小的数组装载这个新数组,比较时用原数组,放置时用开好的新数组。因为递归时空间可以复用,所以归并排序的空间复杂度明显是O(N)。
时间复杂度:
时间复杂度是容易判断,由递归的深度和判断的次数即可得出归并排序的时间复杂度,二分法将递归深度变为log(N),数据量为N,故时间复杂度为O(N*logN)。
递归实现:
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perroe("malloc fail");return;}_MergeSort(a, tmp, 0, n - 1);free(tmp);
}
void _MergeSort(int* a, int* tmp, int begin, int end)
{if (end <= begin)return;int mid = (end + begin) / 2;MergeSort(a, tmp, begin, mid);MergeSort(a, tmp, mid + 1, end);//归并到tmp数组,再拷贝回去//a->[begin,mid][mid+1,end]->tmp拷贝过去,新开空间int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int index = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
要注意递归的结束条件已经想要用递归来做什么,不断分化小区间,然后调用小区间的归并,直至每个数组只有一个元素,然后再用两个有序数组合并为一个有序数组的方法,将两个数组合并。
上图展开中好似前半段和后半段的排序是同时进行的,其实不然,根据代码就可以看出,递归先排序好数组的前半部分,再排序数组的后半部分。

在分割时是有顺序的,如果递归的过程还是不够清晰可以自己尝试画一画递归展开图,也可移步二叉树问题详谈递归对递归的过程获得更大的理解和掌握。
迭代实现
无疑是借助==循环(迭代)==来实现。
仔细想一想我们会发现,在递归的过程中我们需要的是不断获得分割后每一小区间数组的坐标,分割直至每一个小数组只有一个元素为止,然后一个数组有两个元素,然后继续合并为八个元素,直至数组的每个坐标的值都被访问一遍为止。
如果大家已经看了快速排序的非递归版,可能会想到用栈来实现,然而这里用栈是不能解决这里的问题的,快速排序可以用栈是因为数组个数end在使用之后就pop出栈也没有影响,然而归并排序还需要知道划分的范围最后要合并数组,然而如果想要实现递归的过程,前边的数据都已经被pop掉,无法确定数组范围,就无法借此来合并。
如动图所示:

当然,如果一定要用栈或队列来实现他,会很麻烦,因为有更好的方法可以解决。
要跳出递归的思路,利用循环的方法,归并的思想。
如图所示

首先一个一个元素排序合并,两个两个元素进行排序并合并,两两排序后,每两个元素就变成有序的了,然后四个四个合并并排序,然后八个和八个,这样就将数组所由元素利用归并的方式进行排序。
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//[begin1,end1] [begin2,end2]归并//如果第二组不存在,这一组就不用归并啦if (begin2 >= n){break;}//如果第二组越界if (end2 >= n){end2 = n - 1;}int index = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}printf("\n");gap *= 2;}free(tmp);
}
下边是上述代码的解释:
可以看到,起始条件下gap的值为1,第一次循环时,将begin1为0,end1为0,begin2为1,end2为1。
判断大小,将小的放前边,大的放后边,最后归并到原数组。memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));
由于i=0。拷贝回原数组时,a+i还是a的位置,拷贝数量在-0+1后变为了2,就将判断后的两个元素归并到原数组,且已经排好了序。
- 然后下次循环,i+2,指向了数组第三个元素。
begin1=2,end1=2,begin2=3,end2=3。
这时就是第二个元素第三个元素排序归并,直至走完这一次for循环,gap*=2,回到外层while循环,gap<n继续走,此时gap为2,再次进入for循环时,每次跳跃的间隔就是2,就实现了上边所说,将数组依次分为一个和一个排序归并,两个两个排序归并,然后4个和4个归并。。。。。。
注意:这里while结束的条件为gap>n,在循环内,一定会出现这样的情况,虽然gap的值没有大于n,但在for循环中,i的值加等于二倍的gap,所以begin2一定会大于n,这就会造成越界访问,这时就不应该继续执行循环,直接break出去,然后在while循环结尾,gap会*=2,当gap的值大于n时,就代表数组已经排序完了。
//如果第二组不存在,这一组就不用归并啦if (begin2 >= n){break;}
还有一种情况就是begin2没有越界,然而end2越界,这时第二个数组还是存在的,直接将end2更改为n-1即可。
if (end2 >= n)
{end2 = n - 1;
}
稳定性分析:
归并排序是一个稳定的排序,除了空间复杂度比较大,其他的都是优点,通过上边的演示,可以发现,在归并的过程中相同数据的位置排列不会发生变化。
总结:
归并排序是一种很不错的排序方式,如果追求高效率且需要稳定性,归并排序是首当其冲的最优解,对于当前的计算机来说花费一点内存不算什么,归并排序的思想很简单,困难的是细节的把握,相对于其他相同时间复杂度的其他排序方式,大都是不稳定的,所以总体而言归并排序在排序界还是有一席之地的。
今天的内容就到这里,欢迎大家留言反馈。

相关文章:

归并排序(含递归和非递归版)
以梦为马,不负韶华 文章目录 引入:实现原理问题引出:递归实现:迭代实现稳定性分析:总结: 引入: 如何将两个有序数组(假设为升序)合并为一个有序数组? 双指针…...
微服务的注册发现和微服务架构下的负载均衡
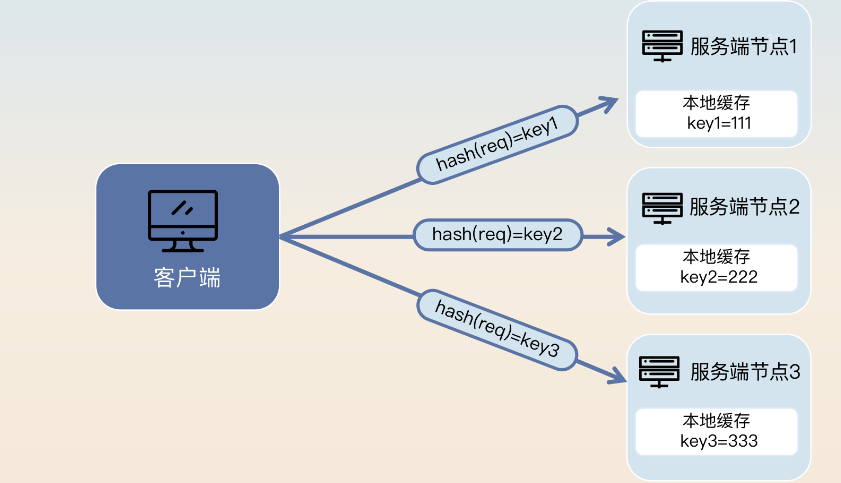
文章目录 微服务注册模型服务注册与发现怎么保证高可用【1. 服务端崩溃检测】【2. 客户端容错】【3. 注册中心选型】 微服务架构下的负载均衡【1.轮询与加权轮询】【2.随机与加权随机】【3.哈希与一致性哈希】【4.最少连接数】【5.最少活跃数】【6.最快响应时间】【总结】 负载…...

从混沌到有序:sortedcontainers库的数据魔法改变你的编程体验
前言 在当今数据爆炸的时代,高效地处理和操作数据成为每位Python开发者的核心任务。在这个背景下,sortedcontainers库以其强大的有序数据结构为程序员提供了处理大规模数据的优越选择。本文将深入研究sortedcontainers库中的主要有序数据结构࿰…...

读取pdf、docx、doc、ppt、pptx并转为txt
文章目录 一、思路构建二、开始实现三、存在的问题3.1 解析doc文档遇到问题及解决方法:3.2 解析ppt文档遇到问题及解决方法: 四、读取pdf中的图片 一、思路构建 Zip文件和初始化文件放在同一个文件夹下;然后解析zip文件读取到一个新的文件夹…...
11.13/14 理解SDK框架遇到的问题
1.1.浮点数打印问题 float red_increment (target_red_value - initial_red_value) / STEPS; u8 STEPS 100; printf("绿色值每一次增量------%f\n", red_increment); 后面三个参数均为u8类型 希望采用 %f打印出每次的步进值。但是结果为空白 希望采用 %.2f打印…...
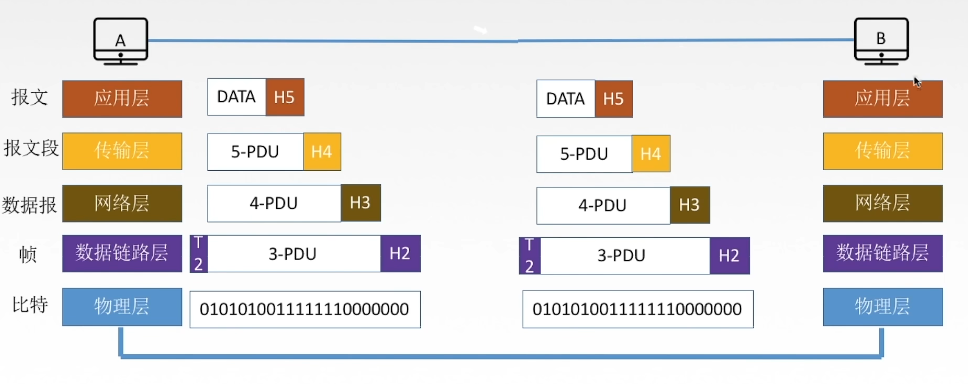
计算机网络——b站王道考研笔记
第一章 计算机网络体系结构 1.计算机网络概述 (1)概念 计算机网络是一个将分散的,具有独立功能的计算机系统,通过通信设备与线路连接起来,由功能完善的软件实现资源共享和信息传递的系统; 是互连的&#…...

Stm32_标准库_18_串口蓝牙模块_手机与蓝牙模块通信_控制LED灯亮灭
通过输入LED_ON和LED_OFF分别控制LED灯的亮与灭 接线: LED的正极接正电,负极接GPIOA_Pin1 蓝牙模块TXD接GPIOA_Pin3,VCC接正电,GND接负电 注意:USART2是APB1外设,汉字占用字节数是字符的两倍 使用: 手…...

低代码与传统开发:综合比较
近年来,低代码开发作为软件开发的趋势获得了显着的发展势头。根据 MarketsandMarkets 的数据,低代码开发市场预计将实现 28.1% 的大幅增长率,到 2025 年价值将达到 455 亿美元。这一显着增长表明了各行业和企业对低代码平台的需求和采用不断增…...
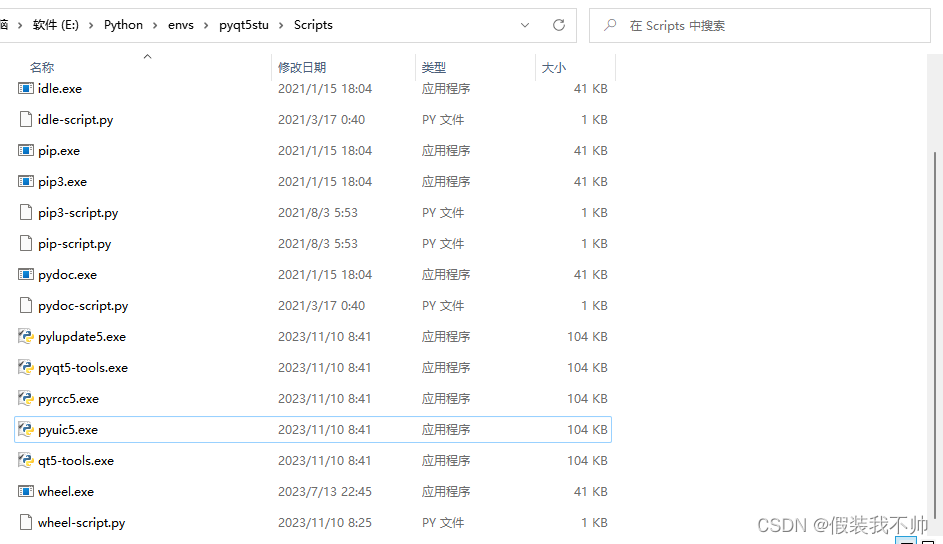
pyqt环境搭建
创建虚拟环境 # 用管理员身份运行 conda create --prefixE:\Python\envs\pyqt5stu python3.6 # 激活虚拟环境 conda activate E:\Python\envs\pyqt5stu # 退出虚拟环境 conda deactivate安装包 pip install PyQt5 -i https://pypi.douban.com/simple pip install PyQt5-tools…...
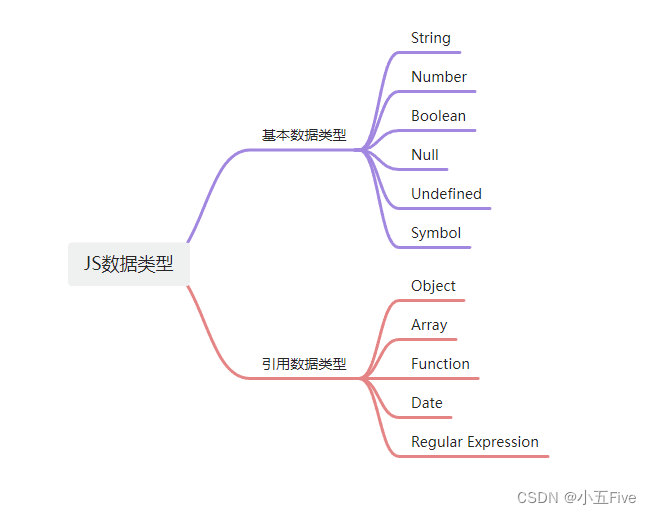
JavaScript数据类型和存储区别
目录 一、原始数据类型 二、引用数据类型 三、存储区别 四、常见错误 JavaScript是一种动态类型语言,这意味着变量可以在程序执行过程中改变其数据类型。了解JavaScript中的数据类型和它们的存储方式对于编写高效和可维护的代码至关重要。 在JavaScript中&…...
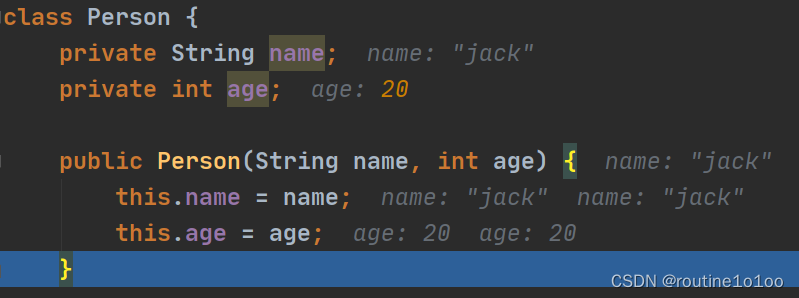
Java学习笔记(七)——面向对象编程(中级)
一、IDEA (一)常用的快捷键 (二)模版/自定义模版 二、包 (一)包的命名 (二)常用的包 (三)如何引入(导入)包 (四&am…...
详细推导MOSFET的跨导、小信号模型、输出阻抗、本征增益
目录 前言 什么是跨导 什么是小信号模型 什么是输入阻抗和输出阻抗 什么是MOS管的输出阻抗 什么是MOS管的本征增益 共源极放大电路的输入和输出阻抗 一些其它MOS拓扑电路的增益 负载为恒流源 负载为二极管 前言 相信很多人在学习集成电路领域的时候 都对MOS管的…...

循环2作业
第一题 #include <stdio.h>int main() {int n,f,y,i,j;scanf("%d",&n);for(y0;y<100;y)for(f0;f<100;f)if(200*y2*ff*100y-n){printf("%d.%d",y,f);return 0;}printf("%d No Solution",n);return 0; }第二题 #include<stdi…...
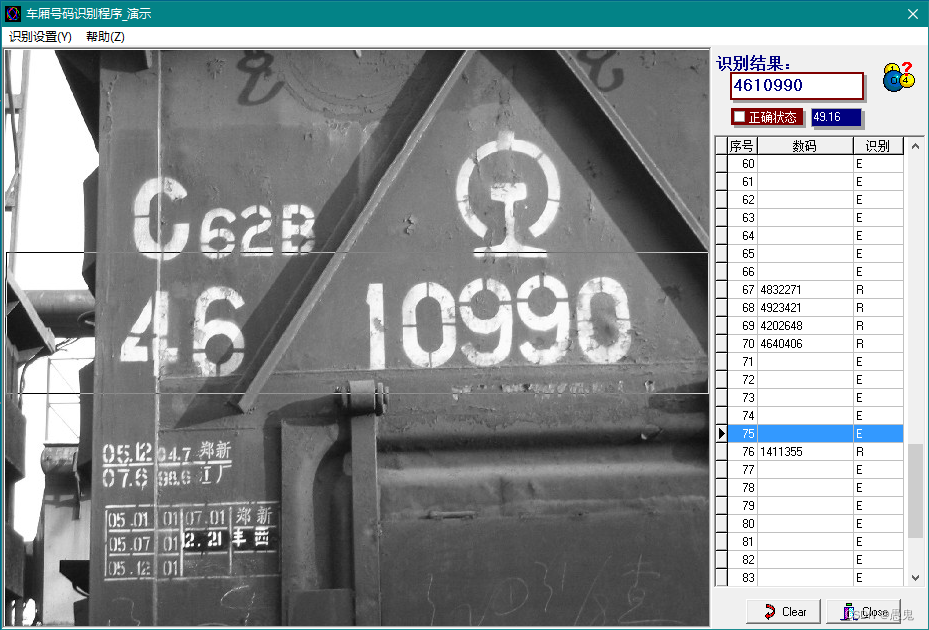
一个车厢号码识别算法(2005年的老程序----ccc)
一个车厢号码识别算法(2005年的老程序----ccc) 2023-09-18 ccc 程序的识别效果 对图中的车厢号码部分用上下两条线限定分为,然后进行识别。 从上面的识别效果可以看出,识别算法具有一定的鲁棒性,能够适应车厢号码的各…...
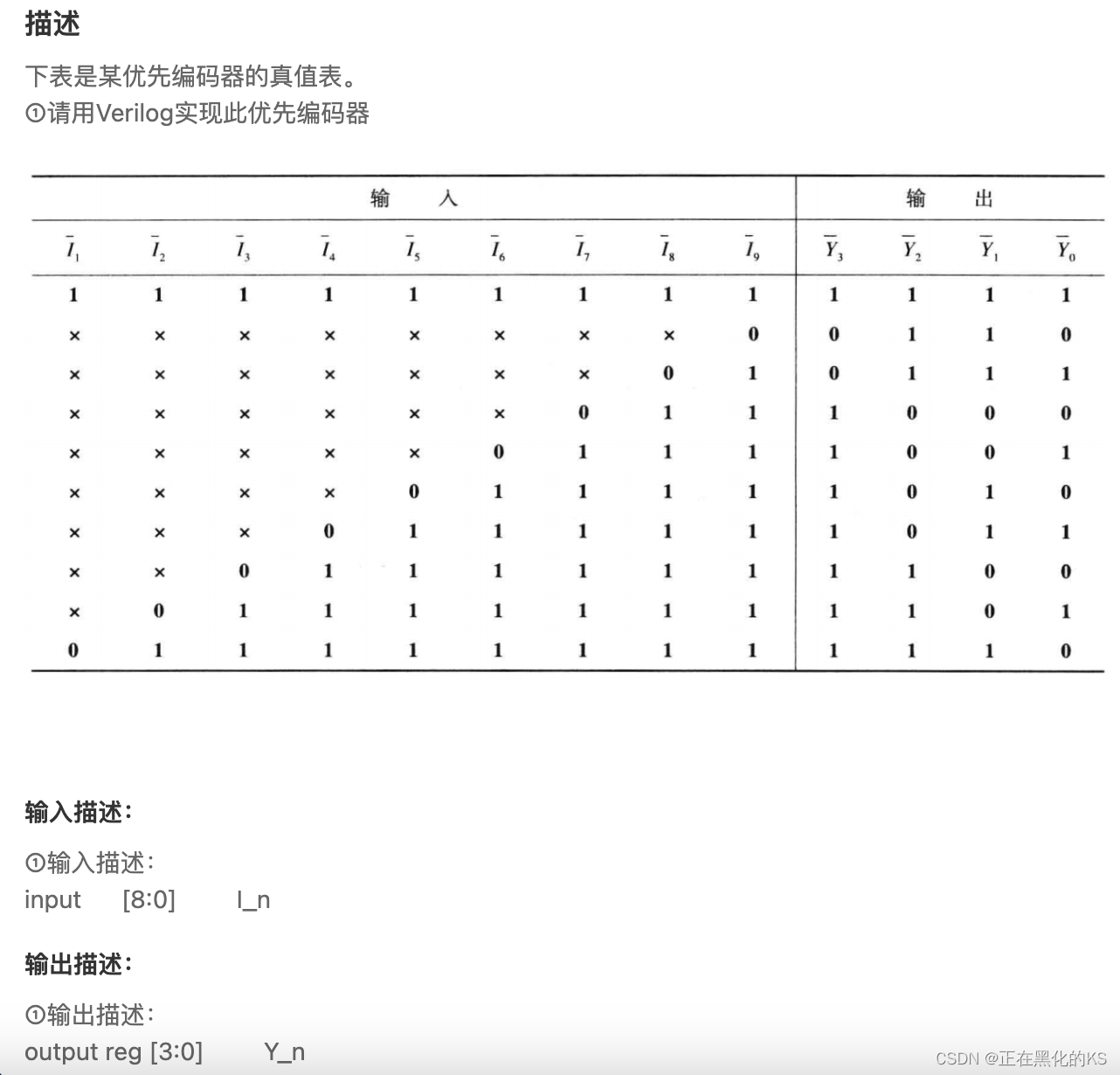
「Verilog学习笔记」优先编码器电路①
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 timescale 1ns/1ns//优先编码器电路1 //电路的优先顺序是,从9到1,高级到低级 //9个输入端:I端,4个输出端:Y端&am…...
解决企业项目管理难题:痛点分析与实用解决方案探索
在当前竞争激烈的商业环境中,产品力已然成为市场竞争的核心,这背后的驱动力是技术、人才和管理能力的综合体现——研发创新能力。其中,项目管理能力扮演着至关重要的角色,它能最大化地发挥和释放以上三者的优势。因此,…...
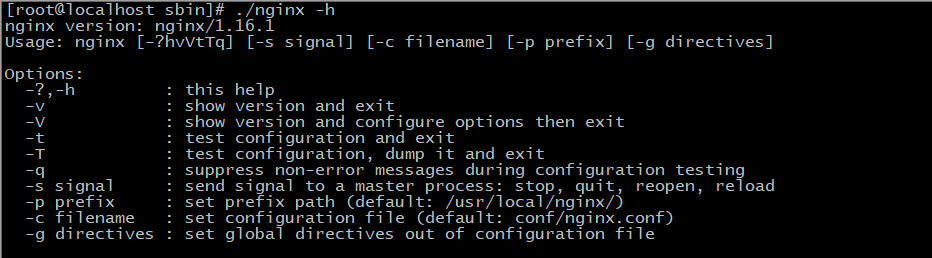
Nginx 简介和安装
文章目录 介绍Nginx的优点(1)速度更快、并发更高(2)配置简单,扩展性强(3)高可靠性(4)热部署(5)成本低、BSD许可证 Nginx的功能特性及常用功能基本HTTP服务高级HTTP服务邮件服务Nginx常用的功能模块 Nginx环境准备docker安装乌班图安装Nginx目录结构分析方式一:Nginx…...
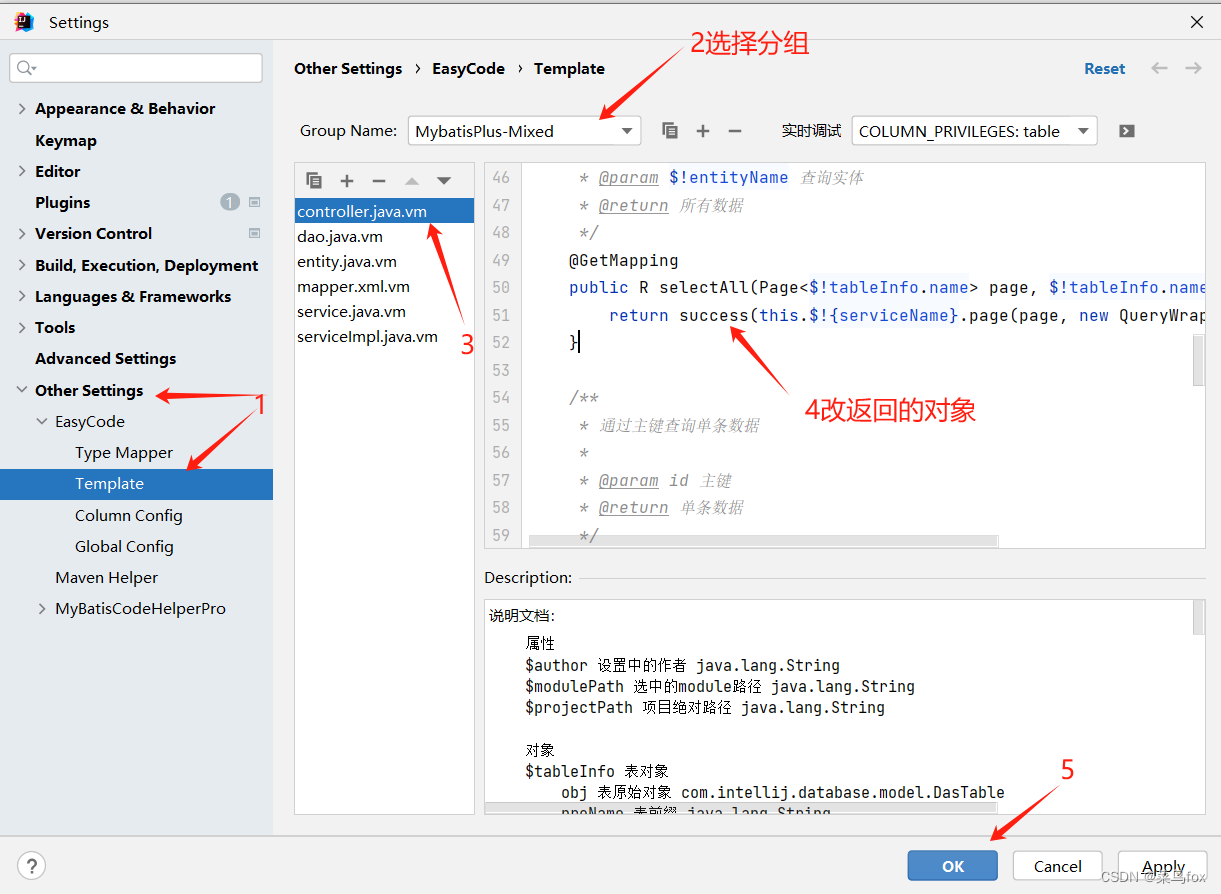
idea生成代码(一):实现java语言的增删改查功能(基于EasyCode插件)支持自定义模板【非常简单】
idea生成代码(一):实现java语言的增删改查功能(基于EasyCode插件)支持自定义模板【非常简单】 idea生成代码(二):实现java语言的增删改查功能(基于mybatis-plus代码生成器…...

vue预览各种格式图片png jpg tif tiff dcm
// 没有图片展示暂无 有图片,判断格式 png jpg 直接展示 tif tiff需要转化成png展示 dcm需要用到插件 <el-col :span"16"><div style"width:100%;text-align: center;margin-bottom: 10px;">图件预览</div><div style&quo…...
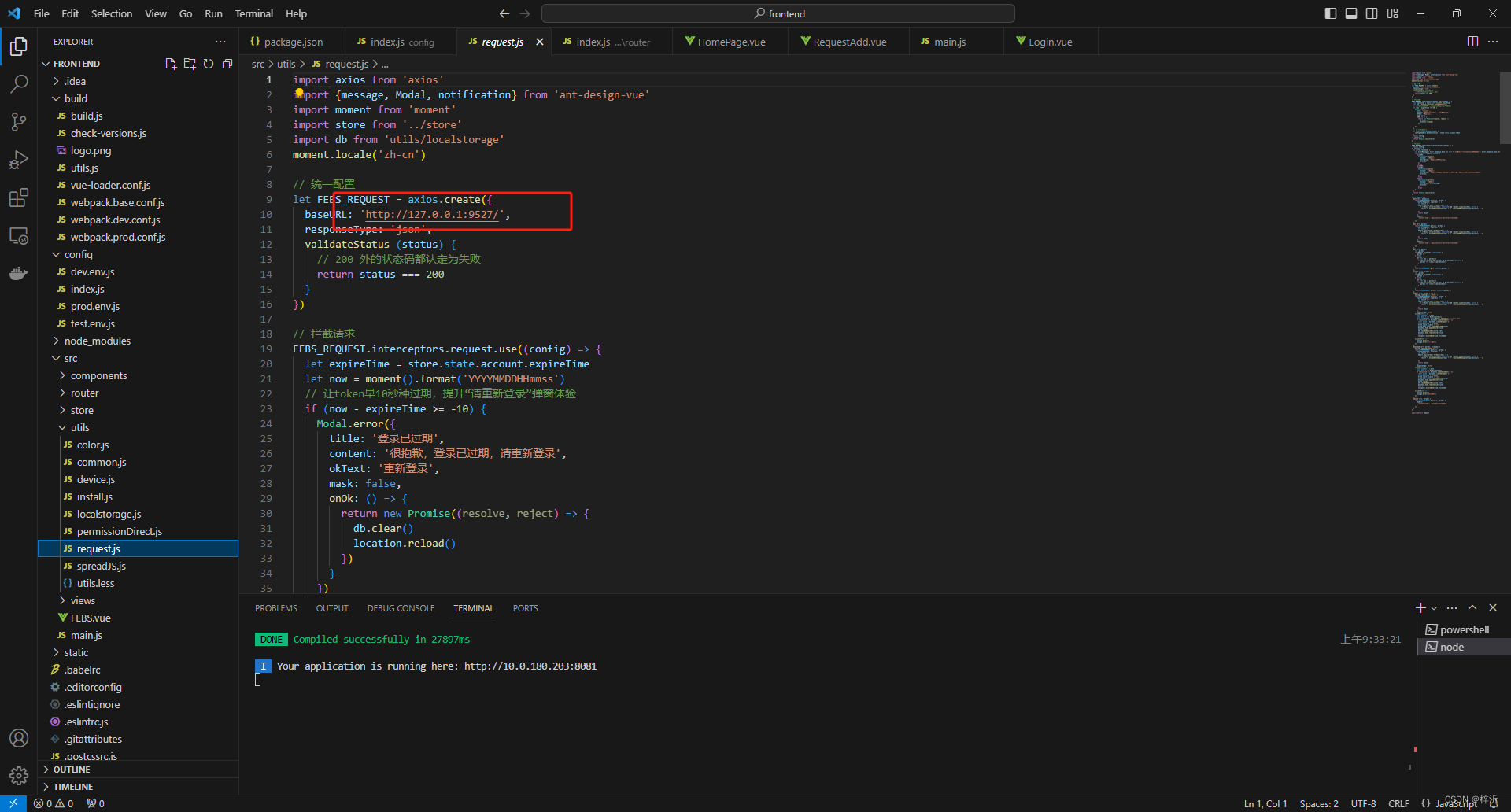
出入库管理系统vue2前端开发服务器地址配置
【精选】vue.config.js 的完整配置(超详细)_vue.config.js配置_web学生网页设计的博客-CSDN博客 本项目需要修改两处: 1、vue开发服务器地址:config\index.js use strict // Template version: 1.3.1 // see http://vuejs-templa…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

