【数据结构】堆(Heap):堆的实现、堆排序、TOP-K问题
目录
堆的概念及结构
编辑
堆的实现
实现堆的接口
堆的初始化
堆的打印
堆的销毁
获取最顶的根数据
交换
堆的插入(插入最后)
向上调整(这次用的是小堆)
堆的删除(删除根)
向下调整(这次用的小堆)
堆排序
TOP-K问题
堆的概念及结构
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
小根堆:父亲节点大于等于孩子节点
大根堆:父亲节点小于等于孩子节点

堆的实现
实现堆的接口
#define CRT_SECURE_NO_WARNING 1
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>
#include<stdbool.h>//二叉树-堆
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void AdjustUp(HPDataType* a, int child);void AdjustDown(HPDataType* a, int n, int parent);//交换
void Swap(HPDataType* p1, HPDataType* p2);
//打印
void HeapPrint(HP* php);
//初始化
void HeapInit(HP* php);
//
void HeapInitArray(HP* php, int* a, int n);
//销毁
void HeapDestroy(HP* php);
//插入
void HeapPush(HP* php, HPDataType x);
//删除
void HeapPop(HP* php);
//返回最顶数据
HPDataType HeapTop(HP* php);
//判空
bool HeapEmpty(HP* php);堆的初始化
//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}堆的打印
void HeapPrint(HP* php)
{assert(php);//最后一个孩子下标为size-1for (size_t i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}
堆的销毁
//销毁
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}获取最顶的根数据
//获取根数据
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}
交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}堆的插入(插入最后)
先考虑扩容,将数据插到最后,再用向上调整法。
//插入数据
void HeapPush(HP* php, HPDataType x)
{assert(php);//扩容if (php->size == php->capacity)//有效元素个数和容量是否相等{//相等的情况分两种:1.容量为0,先扩4个sizeof 2.容量占用满了,扩2个int newCapacity =php->capacity == 0 ? 4 : php->capacity * 2;//返回扩容后的内存新地址 //扩容后的新大小HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}//扩容后的新地址php->a = tmp;//新容量php->capacity = newCapacity;}// php->size下标位置 先将x放最后,后面再调整php->a[php->size] = x;// 有效数据++php->size++;// 向上调整 //size-1为新插入数据的下标AdjustUp(php->a, php->size - 1);}向上调整(这次用的是小堆)
向上调整的前提:左右子树是堆 ,时间复杂度O(logN)
//向上调整 //新插入的数据下标
void AdjustUp(HPDataType* a, int child)
{ //定义其父节点的下标int parent = (child - 1) / 2;//循环while (child > 0){//如果子小于父就交换 (小堆)if (a[child] < a[parent]){//数值交换Swap(&a[child], &a[parent]);//下标child = parent;parent = (parent - 1) / 2;}else{break;}}
}堆的删除(删除根)
先判空,看下是否还有元素可以删除。根数据先和最后一个孩子交换位置,孩子再向下调整。
//删除
void HeapPop(HP* php)
{assert(php);//确保有元素可删assert(php->size > 0);//最后一个孩子和要删除的根交换Swap(&php->a[0], &php->a[php->size - 1]);//有效元素size减减,相当于删除了交换后的原来的根--php->size;//删除后向下调整AdjustDown(php->a, php->size, 0);}向下调整(这次用的小堆)
向下调整的前提:左右子树是堆
//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//n下标位置已经没有数了while (child < n){//选小的孩子往上浮(小堆)if (child + 1 < n && a[child + 1] < a[child]){++child;}//若小的孩子都小于父,则交换if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//交换后下来的数重新变成parent,继续向下调整parent = child;child = parent * 2 + 1;}}
}堆排序
void HeapSort(int* a, int n)
{//建堆 这里可以选建大堆还是小堆// 向下调整建堆// O(N)for (int i = (n-1-1)/2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}TOP-K问题
先创建一个包含有10000000个数的data.txt文本文件。
void CreateNDate()
{// 造数据int n = 10000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 10000000;fprintf(fin, "%d\n", x);}fclose(fin);
}前k个建小堆(堆顶元素为k中最小),剩余n-k个依次和堆顶元素比较,比k大就插入堆中(插入堆插入向下调整法),完成后打印前k个元素。
void PrintTopK(const char* filename, int k)
{// 1. 建堆--用a中前k个元素建堆FILE* fout = fopen(filename, "r");if (fout == NULL){perror("fopen fail");return;}//给堆开辟空间int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc fail");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);}// 前k个数建小堆for (int i = (k - 2) / 2; i >= 0; --i){AdjustDown(minheap, k, i);}// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){// 替换你进堆minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");free(minheap);fclose(fout);
}
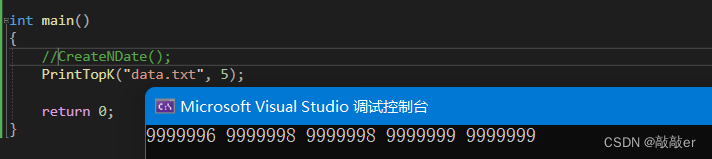
假设k等于5,成功打印出前5个最大的数据

相关文章:

【数据结构】堆(Heap):堆的实现、堆排序、TOP-K问题
目录 堆的概念及结构 编辑 堆的实现 实现堆的接口 堆的初始化 堆的打印 堆的销毁 获取最顶的根数据 交换 堆的插入(插入最后) 向上调整(这次用的是小堆) 堆的删除(删除根) 向下调整(这次用的…...

保护数字前沿:下一代防火墙如何塑造网络安全的未来
下一代防火墙通过提供先进的威胁检测、精细控制和云安全功能,正在重塑网络安全的未来。随着数字环境的不断发展,组织必须采用这些创新解决方案来保护其数字资产并维护安全的数字前沿。 在当今互联的世界中,网络威胁变得越来越复杂,…...

深入理解Java中的String.join方法
在 Java 编程中,字符串操作是非常常见的需求。在 Java 8 中引入了一个方便的字符串连接方法 String.join,它能够简洁而高效地将多个字符串连接起来。本篇博客将深入介绍 String.join 方法的使用和原理。 什么是String.join方法? String.join…...

【MySQL系列】 第三章 · 函数
写在前面 Hello大家好, 我是【麟-小白】,一位软件工程专业的学生,喜好计算机知识。希望大家能够一起学习进步呀!本人是一名在读大学生,专业水平有限,如发现错误或不足之处,请多多指正࿰…...

微信小程序wxss定位/选择/查找元素的几种方式
wxss定位、选择、查找元素的几种方式与css类似,下面介绍常用的几种: 选择器样例样例描述.class.intro选择所有拥有 class"intro" 的组件#id#firstname选择拥有 id"firstname" 的组件elementview选择所有 view 组件element, element…...

Canvas—从入门到案例实现
文章目录 Canvas—从入门到案例实现一、设置canvas环境1.1 <canvas>元素1.2 渲染上下文context 二、形状与路径的绘制2.1 形状绘制2.2 路径绘制2.3 绘制一个笑脸 三、使用样式和颜色四、绘制文本五、使用图像5.1 图片源5.2 获取页面内的图片5.3 缩放Scaling5.4 切片Slici…...
飞书开发学习笔记(六)-网页应用免登
飞书开发学习笔记(六)-网页应用免登 一.上一例的问题修正 在上一例中,飞书登录查看网页的界面显示是有误的,看了代码,理论上登录成功之后,应该显示用户名等信息。 最后的res.nickName是用户名,res.i18nName.en_us是英…...

【ROS】Nav2源码下载、编译、运行
【ROS】郭老二博文之:ROS目录 1、源码下载 1.1 源码地址 https://github.com/ros-planning/navigation2 1.2 创建工程目录 ROS2使用目录结果来管理项目,因此在下载前需要创建好目录结构: mkdir -p ~/git/nav2/src1.3 下载 git中默认版本是main。本人的开发环境为Ubun…...

微信小程序 30分钟倒计时功能
ps:凑个数 getTimeDiff(date) {let _this = this;let curTime = new Date(date)_this.countDown(_this.timeFormatConvert(new Date(curTime.setMinutes(curTime.getMinutes() + 30))))},timeFormatConvert(e) {const Y = e.getFullYear(); // 年const M = this.prefixZero(e.…...

JAVA判断指定日期是否在指定的时间段内
参考文献: Java语言判断当前时间在时间范围内_java判断时间区间-CSDN博客 package com.itheima.method2;import java.text.ParseException; import java.text.SimpleDateFormat; import java.util.Calendar; import java.util.Date;public class DateTest {public static voi…...

关于晋升与跳槽的一些思考
内部晋升 内部晋升是我优先考虑的,原因有很多。首先这是一个新业务,相对而言容易拿到结果。其次我想体验不同的晋升路径,内部晋升答辩,是挑战也是一次成长的机会,是一次他人帮助自己review的机会。作为从校园出来的校…...
url找不到404的问题,url被拼接
今天遇到一个测试feign调用的功能,如图所示 先说结论 Controller换成RestController 将日志设置为debug模式 被DispatcherServlet FORWARD了 找到路径 对属性设置断点,看下是哪注进来的 我们再去找encodedPath 此处是undertow的源码,但是und…...

如何解决golang开发中遇到的报错:checksum mismatch downloaded
问题描述 如题,项目开发中遇到如下报错(你的报错信息可能与我的有一点区别,如verifying的包名,但是问题本质都是一样的): verifying github.com/algorand/go-codec/codecv1.1.8/go.mod: checksum mismatc…...

4.以docker容器生成镜像推送到阿里云镜像仓库
1.开通阿里云镜像仓库 1.1 登录阿里云,访问容器镜像服务。地址如下: https://cr.console.aliyun.com/cn-shanghai/instances 1.2 个人学习为例,创建个人版实例 1.2.1 点击个人实例 1.2.2 .创建个人实例 1.2.3 创建完成后,设置…...

CSS Form表单布局
效果图 <Tab IsCard"true"><TabItem Text"表单信息-DIV版本"><div class"row"><div class"col"><label for"field1">工程名称:</label><input class"form-control" type&…...

c++ shared_mutex 读写锁使用详解
c 读写锁使用详解 std::shared_mutex c17 头文件 #include <shared_mutex>。用于实现共享和独占访问的互斥锁。提供了一种更加灵活的机制,允许多个线程在共享模式下读取数据,但只允许单个线程在独占模式下写入或修改数据。与 std::mutex 相比&am…...

淘宝商品详情接口,淘宝详情页接口,宝贝详情页接口,商品属性接口,商品信息查询,商品详细信息接口,h5详情,淘宝API接口演示案例
淘宝详情接口API可以帮助简化运营流程,更加专注于产品本身。通过调用API,可以快速获取到商品的标题、图片、价格等信息,省去了手动编写和编辑的繁琐过程。这样就可以更快地上架新品、更新商品信息,提高运营的效率。 taobao.item_…...
python爬取网站数据,作为后端数据
一. 内容简介 python爬取网站数据,作为后端数据 二. 软件环境 2.1vsCode 2.2Anaconda version: conda 22.9.0 2.3代码 链接: 三.主要流程 3.1 通过urllib请求网站 里面用的所有的包 ! pip install lxml ! pip install selenium ! pip install…...
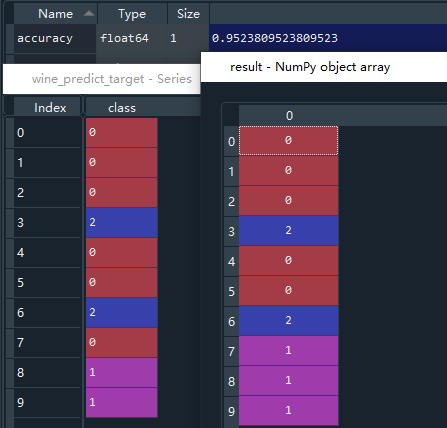
【机器学习】K近邻算法:原理、实例应用(红酒分类预测)
案例简介:有178个红酒样本,每一款红酒含有13项特征参数,如镁、脯氨酸含量,红酒根据这些特征参数被分成3类。要求是任意输入一组红酒的特征参数,模型需预测出该红酒属于哪一类。 1. K近邻算法介绍 1.1 算法原理 原理&a…...

基于安卓android微信小程序的快递取件及上门服务系统
项目介绍 本文从管理员、用户的功能要求出发,快递取件及上门服务中的功能模块主要是实现管理员服务端;首页、个人中心、用户管理、快递下单管理、预约管理、管理员管理、系统管理、订单管理,用户客户端;首页、快递下单、预约管理…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

