2023年亚太杯数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录
- 0 赛题思路
- 1 描述
- 2 问题概括
- 3 建模过程
- 3.1 边界说明
- 3.2 符号约定
- 3.3 分析
- 3.4 模型建立
- 3.5 模型求解
- 4 模型评价与推广
- 5 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 描述
某大学数学系人力资源安排问题是一个整数规划的最优化问题,通过具体分析数学系现有的技术力量和各方面的约束条件,在问题一的求解中,可以列出一天最大直接收益的整数规划,求得最大的直接收益是42860元;而在问题二的求解中,由于教授一个星期只能工作四天,副教授一个星期只能工作五天,在这样的约束条件下,列出一个星期里最大直接收益的整数规划模型,求得其最大直接收益是198720元。
2 问题概括
数学系的教师资源有限,现有四个项目来源于四个不同的客户,工作的难易程度不一,各项目对有关技术人员的报酬不同。所以:
1.在满足工作要求的情况下,如何分配数学系现有的技术力量,使得其一天的直接收益最大?
2.在教授与副教授工作时间受到约束的条件下,如何分配数学系现有的技术力量,使得其在一个星期里的直接收益最大?
3 建模过程
3.1 边界说明
1.不同技术力量的人每天被安排工作的几率是相等的,且相同职称的个人去什么地方工作是随机的;
2.客户除了支付规定的工资额外,在工作期间里,还要支付所有相关的花费(如餐费,车费等);
3.当天工作当天完成.
3.2 符号约定

3.3 分析
由题意可知各项目对不同职称人员人数都有不同的限制和要求.对客户来说质量保证是关键,而教授相对稀缺,因此各项目对教授的配备有不能少于一定数目的限制.其中由于项目技术要求较高,助教不能参加.而两项目主要工作是在办公室完成,所以每人每天有50元的管理费开支.
由以上分析可得:最大直接收益=总收益-技术人员工资-、两地保管费.
3.4 模型建立



3.5 模型求解
相关数据表格如下:
数学系的职称结构及工资情况
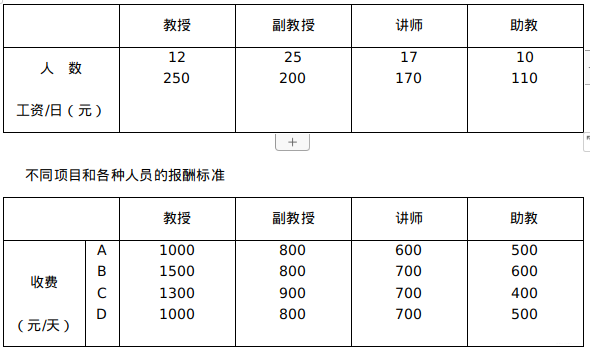
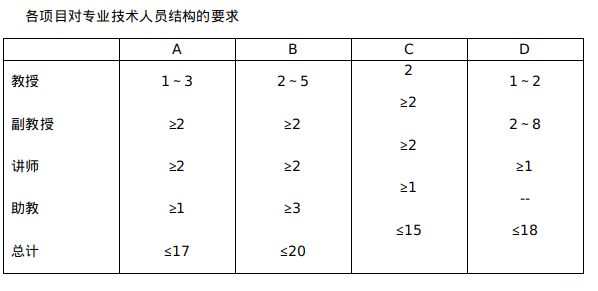
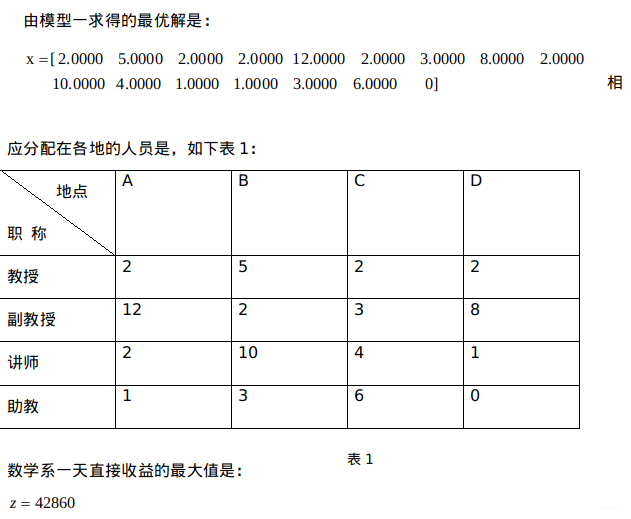
4 模型评价与推广
本模型通过合理的假设,充分考虑各方面的限制条件,得出的人员安排和直接收益
都是本模型的最优解与最优值,对武汉大学数学系的人力资源安排有一定的指导作用。但从模型假设中,我们可以知道对数
学系现有的技术力量的安排是随机的,在相同工作时段里,可能会出现部分人工作次数较多,而部分人较少的不公平情况。
所以在满足工作需求的情况下,分配工作时应该要人为地尽量使得每个人的工作次数不要相差太远,或者相等。
此模型通过对人力资源的调配,从量化的角度得出数学系的最大直接收益。利用此模型的方法可以求出所有类似本模型的线性规划模型。但是,本模型只是单目标的规划,可以在此基础上,增加目标要求。如在数学系的直接收益尽可能大的基础上,使得客户所花费的资金最少,等等。从而建立多目标规划模型。解决更为复杂的实际问题。
5 实现代码
f=[-1000;-800;-550;-450;-1500;-800;-650;-550;-1300;-900;-650;-350;-1000;-800;-650;-450];
A=zeros(9,16);
for i=1:1for j=1:16A(i,j)=1; end
end
for i=2:5for j=i-1:4:11+iA(i,j)=1;end
end
i0=0;
for i=6:9for j=i0+1:(i-5 )*4A(i,j)=1;endi0=j;
end
b=[64;17;20;15;18;12;25;17;10];
Aeq=zeros(1,16);
Aeq(1,3)=1;
beq=[2];
LB=[1;2;2;1;2;2;2;2;2;2;2;1;1;3;1;0];
UB=[3;5;2;2;inf;inf;inf;8;inf;inf;inf;inf;inf;inf;inf;0];
[x,fval]=linprog(f,A,b,Aeq,beq,LB,UB)f=[-1000;-1000;-1000;-1000;-1000;-1000;-1000;-1500;-1500;-1500;-1500;-1500;-1500;-1500;-1250;-1250;-1250;-1250;-1250;-1250;-1250;-950;-950;-950;-950;-950;-950;-950;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-850;-850;-850;-850;-850;-850;-850;-750;-750;-750;-750;-750;-750;-750;-600;-600;-600;-600;-600;-600;-600;-700;-700;-700;-700;-700;-700;-700;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-500;-500;-500;-500;-500;-500;-500;-600;-600;-600;-600;-600;-600;-600;-350;-350;-350;-350;-350;-350;-350;-450;-450;-450;-450;-450;-450;-450];
A=zeros(60,112);
for i=1;1for j=1:112A(i,j)=1;end
end
i0=0;
for i=2:4for j=i0+1:(i-1)*28A(i,j)=1;endi0=j;
end
for i=5:32for j=(i-4):28:80+iA(i,j)=1;end
end
for i=33:39for j= i-32:7:(i-11)A(i,j)=1;end
end
j0=j;
for i=40:46for j=j0+(i-39):7:(i-18)+j0A(i,j)=1;end
end
j0=j;
for i=47:53for j=j0+(i-46):7:j0+(i-25)A(i,j)=1;end
end
j0=j;
for i=54:60for j=j0+(i-53):7:j0+(i-32)A(i,j)=1;end
end
b=[362;48;125;119;17;17;17;17;17;17;17;20;20;20;20;20;20;20;15;15;15;15;15;15;15;18;18;18;18;18;18;18;12;12;12;12;12;12;12;25;25;25;25;25;25;25;17;17;17;17;17;17;17;10;10;10;10;10;10;10];
UB=[3;3;3;3;3;3;3;5;5;5;5;5;5;5;3;3;3;3;3;3;3;2;2;2;2;2;2;2;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;8;8;8;8;8;8;8;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;0;0;0;0;0;0;0];
LB=[1;1;1;1;1;1;1;2;2;2;2;2;2;2;1;1;1;1;1;1;1;1;1;1;1;1;1;1;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;1;1;1;1;1;1;1;1;1;1;1;1;1;1;3;3;3;3;3;3;3;1;1;1;1;1;1;1;0;0;0;0;0;0;0];
Aeq=zeros(7,112);
for i=1:7Aeq(i,i+14)=1;
end
beq=[2;2;2;2;2;2;2];
[x,fval]=linprog(f,A,b,Aeq,beq,LB,UB)
建模资料
资料分享: 最强建模资料


相关文章:

2023年亚太杯数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录 0 赛题思路1 描述2 问题概括3 建模过程3.1 边界说明3.2 符号约定3.3 分析3.4 模型建立3.5 模型求解 4 模型评价与推广5 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 描述 …...

【广州华锐互动】VR居家防火逃生模拟演练增强训练的真实性
VR软件开发公司广州华锐互动在消防培训领域已开发了多款VR产品,今天为大家介绍VR居家防火逃生模拟演练系统,这是一种基于虚拟现实技术的消防教育训练设备,通过模拟真实的火灾场景,让使用者身临其境地体验火灾逃生过程,…...
)
PaddleClas学习1——使用PPLCNet模型对车辆属性进行识别(python)
使用PPLCNet模型对车辆属性进行识别 1. 配置PaddlePaddle,PaddleClas环境1.1 安装PaddlePaddle(1)创建 docker 容器(2)退出/进入 docker 容器(3) 安装验证1.2 安装python3.8(可选)1.3 安装 PaddleClas2. 模型推理2.1 下载官方提供的车辆属性模型2.2 基于 Python 预测引…...

CSS 实现新拟态(Neumorphism) UI 风格
什么是新拟态(Neumorphism) UI 风格?网上似乎还没有一个准确统一的定义。按照我个人的通俗理解,就是将界面的一部分凸起来,另一部分凹下去,形成的一种错落有致的拟物风格。代表作是乌克兰设计师 Alexander Plyuto 在各平台发布的新…...
)
js 深度学习(六)
立即执行函数 immediate invoked function expression 自动执行 执行完成后立即释放 (function(){var a 1,b2;console.log(ab) }()) // w3c建议 (function(a,b){return ab; })(a,b); // 可以加参数 可以有返回值表达式才能被执行符号执行,被小括号包裹的是表达式…...

【机器学习基础】机器学习的模型评估(评估方法及性能度量原理及主要公式)
🚀个人主页:为梦而生~ 关注我一起学习吧! 💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~ 💡往期推荐: 【机器学习基础】机器学习入门(1) 【机器学习基…...
:useState)
React hooks(一):useState
1.React hooks React hooks是React16.8的新特性,可以让React函数组件具有状态,并提供类似componentDidMount和componentDidUpdate等生命周期方法。 React 早期版本,类组件可以在shouldComponentUpdate中,通过判断props和state是…...
springboot集成swagger3+解决页面无法访问问题
引入依赖 pom文件引入swagger3依赖 <dependency><groupId>io.springfox</groupId><artifactId>springfox-boot-starter</artifactId><version>3.0.0</version></dependency>配置启动文件 swagger使用ant_pattern_parser解析…...

mapreduce-maven--30.串联所有单词的字串
项目对象模型(Project Object Model,POM):Maven使用POM文件来描述项目的结构、依赖和构建设置。POM是一个XML文件,位于项目根目录下,并包含项目的基本信息、构建设置、依赖管理等。 依赖管理:M…...
)
Hive使用max case when over partition by 实现单个窗口取两个窗口的值(单个开窗函数,实际取两个窗口)
一、Hive开窗函数根据特定条件取上一条最接近时间的数据(单个开窗函数,实际取两个窗口) 针对于就诊业务,一次就诊,多个处方,处方结算时间可能不一致,然后会有多个AI助手推荐用药,会…...
2023年【北京市安全员-B证】试题及解析及北京市安全员-B证证考试
题库来源:安全生产模拟考试一点通公众号小程序 北京市安全员-B证试题及解析根据新北京市安全员-B证考试大纲要求,安全生产模拟考试一点通将北京市安全员-B证模拟考试试题进行汇编,组成一套北京市安全员-B证全真模拟考试试题,学员…...

二维码智慧门牌管理系统升级解决方案:流量监控引领服务卓越
文章目录 前言一、流量监控功能概述二、流量监控的益处三、应用案例和成功故事四、实施和支持 前言 随着科技的不断发展,二维码智慧门牌管理系统在其便捷高效的管理方式下,深受广大用户喜爱。为了更好地满足用户需求,提升服务质量࿰…...
)
Linux内核面试题(1)
整理了一些网上的linux驱动岗位相关面试题,如果错误,欢迎指正。 1硬件中断号和Linux内核的IRQ号它们是如何映射的? irq驱动会从dts获取硬件中断号,dts里的interrupts字段,使用gic_irq_domain_translate函数。 然后使…...

wpr -start generalprofile -start pool -filemode 这句命令具体是什么意思
注意事项: 总体而言,WPR 和 WPA 是强大的性能分析工具,通过它们,你可以深入了解系统运行时的性能特性,找出潜在问题并进行优化。 查看详细信息: wpr -start generalprofile -start pool -filemode 对应的结…...

C/CPP基础练习题多维数组,矩阵转置,杨辉三角详解
多维数组 1. 矩阵转置 输入一个数字构成的矩形, 将矩形的值进行转置后打印 输入: 第一行 正整数n(1<n<10), 表示矩阵的边长 随后输入一个矩阵 输出: 转置后的矩阵 样例输入: 3 1 2 3 4 5 6 7 8 9 样例输出: 1 4 7 2 5 8 3 6 9 2. 颈椎病治疗 最近云海学长一…...
父组件用ref获取子组件数据
子组件 Son/index.vue 子组件的数据和方法一定要记得用defineExpose暴露,不然父组件用ref是获取不到的!!! <script setup> import { ref } from "vue"; const sonNum ref(1); const changeSon () > {sonNum.…...

Haskell添加HTTP爬虫ip编写的爬虫程序
下面是一个简单的使用Haskell编写的爬虫程序示例,它使用了HTTP爬虫IP,以爬取百度图片。请注意,这个程序只是一个基本的示例,实际的爬虫程序可能需要处理更多的细节,例如错误处理、数据清洗等。 import Network.HTTP.Cl…...
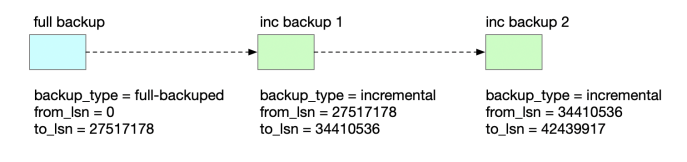
MySQL 社区开源备份工具 Xtrabackup 详解
文章目录 前言1. Xtrabackup 介绍1.1 物理备份与逻辑备份区别1.2 Xtrabackup 系列版本 2. Xtrabackup 部署2.1 下载安装包2.2 二进制部署2.3 程序文件介绍2.4 备份需要的权限 3. Xtrabackup 使用场景3.1 本地全量备份3.2 本地压缩备份3.3 全量流式备份3.3.1 备份到远程主机3.3.…...
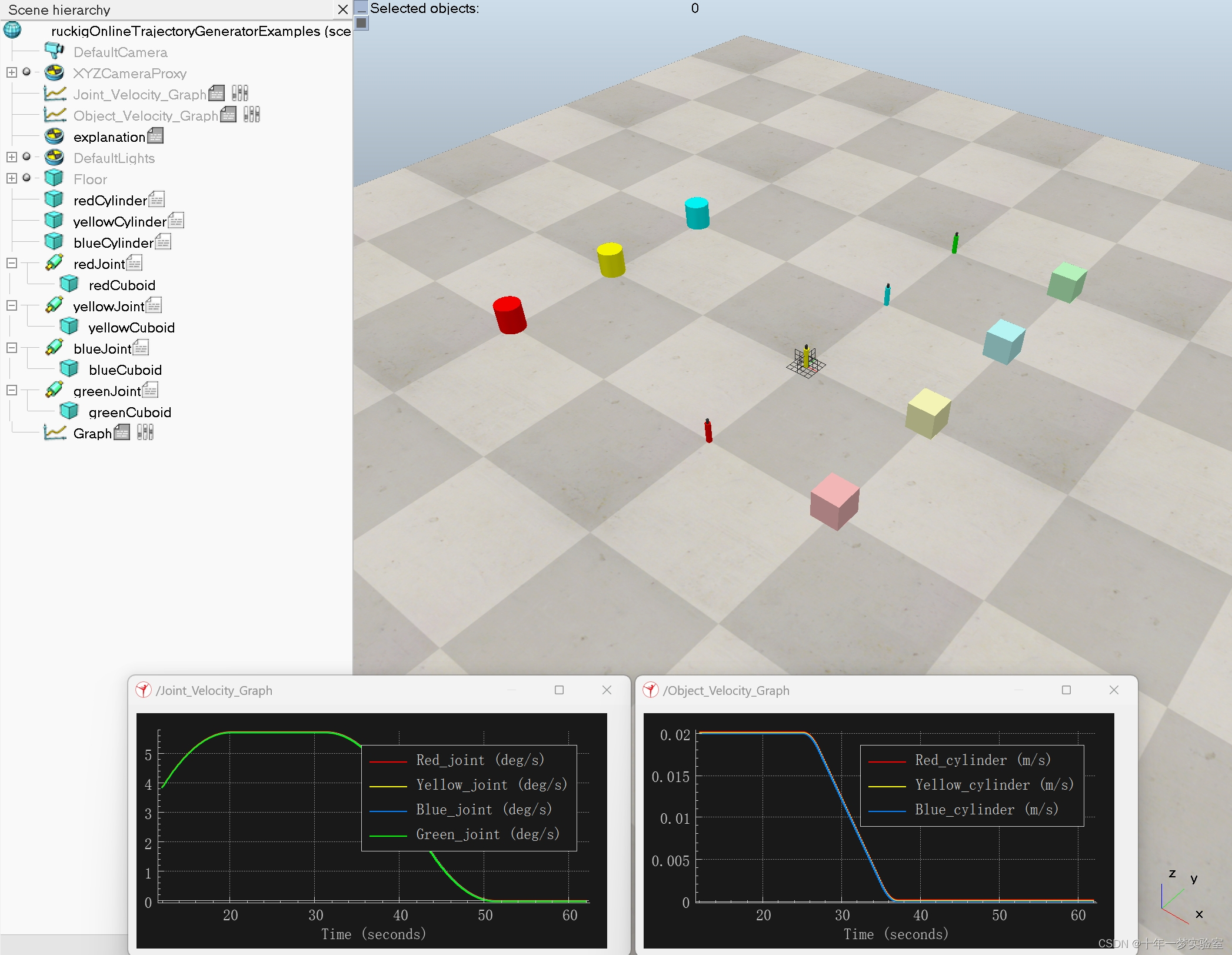
【仿真】ruckig在线轨迹生成器示例
该场景说明了使用 CoppeliaSim 中提供的 Ruckig 在线轨迹生成功能的各种方法: 1. 在线程脚本内使用单个阻塞函数(红色) 2. 在线程脚本中使用多个非阻塞函数(黄色) 3. 在非线程脚本中使用多个非阻塞函数(…...

LeetCode 面试题 16.22. 兰顿蚂蚁
文章目录 一、题目二、C# 题解 一、题目 一只蚂蚁坐在由白色和黑色方格构成的无限网格上。开始时,网格全白,蚂蚁面向右侧。每行走一步,蚂蚁执行以下操作。 (1) 如果在白色方格上,则翻转方格的颜色,向右(顺时针)转 90 度…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
