代码随想录算法训练营Day 54 || 392.判断子序列、115.不同的子序列
392.判断子序列
力扣题目链接(opens new window)
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
示例 1:
- 输入:s = "abc", t = "ahbgdc"
- 输出:true
示例 2:
- 输入:s = "axc", t = "ahbgdc"
- 输出:false
提示:
- 0 <= s.length <= 100
- 0 <= t.length <= 10^4
两个字符串都只由小写字符组成。
双指针法
- 初始化两个指针:
i用于遍历字符串s,j用于遍历字符串t。 - 遍历字符串
t:使用指针j遍历字符串t,对于t中的每个字符,检查是否与s中的当前字符(由i指向)相匹配。 - 匹配字符:如果匹配(即
s[i] == t[j]),则将i和j同时向前移动;如果不匹配,则只将j向前移动。 - 检查是否遍历完
s:如果i等于s的长度,说明s是t的子序列;如果j先达到t的末尾,则说明s不是t的子序列。
def isSubsequence(s: str, t: str) -> bool:i, j = 0, 0while i < len(s) and j < len(t):if s[i] == t[j]:i += 1j += 1return i == len(s)# 测试代码
s1, t1 = "abc", "ahbgdc"
s2, t2 = "axc", "ahbgdc"print(isSubsequence(s1, t1)) # 应该输出 True
print(isSubsequence(s2, t2)) # 应该输出 False
115.不同的子序列
力扣题目链接(opens new window)
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,"ACE" 是 "ABCDE" 的一个子序列,而 "AEC" 不是)
题目数据保证答案符合 32 位带符号整数范围。

提示:
- 0 <= s.length, t.length <= 1000
- s 和 t 由英文字母组成
动态规划思路解析
-
状态定义:
dp[i][j]表示考虑s的前i个字符和t的前j个字符时,t作为s的子序列出现的次数。
-
状态初始化:
dp[0][0] = 1:两个空字符串匹配的次数是1。dp[i][0] = 1对所有i:如果t是空字符串,那么无论s是什么,都只有一种方式使t成为s的子序列(即全部删除s)。
-
状态转移:
- 如果
s的第i个字符与t的第j个字符相同(s[i - 1] == t[j - 1]),那么t的前j个字符可以在s的前i - 1个字符中找到对应的子序列,加上当前匹配的字符,形成新的子序列。同时,t的前j个字符也可能在s的前i - 1个字符中出现多次,不包括s[i]。因此,dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]。 - 如果不同(
s[i - 1] != t[j - 1]),则s的第i个字符不能用于匹配t的第j个字符。这时,dp[i][j] = dp[i - 1][j]。
- 如果
-
最终结果:
dp[len(s)][len(t)]是最终结果,表示s的前len(s)个字符中t的前len(t)个字符作为子序列出现的总次数。
def numDistinct(s: str, t: str) -> int:m, n = len(s), len(t)# 初始化一个 (m+1) x (n+1) 的 dp 矩阵dp = [[0] * (n + 1) for _ in range(m + 1)]# 当 t 为空字符串时,s 的子序列中总有一种方式使得 t 为其子序列for i in range(m + 1):dp[i][0] = 1# 填充 dp 矩阵for i in range(1, m + 1):for j in range(1, n + 1):if s[i - 1] == t[j - 1]:# 如果字符匹配,可以选择使用或不使用 s[i-1]dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]else:# 如果字符不匹配,只能选择不使用 s[i-1]dp[i][j] = dp[i - 1][j]return dp[m][n]# 测试代码
s = "babgbag"
t = "bag"
print(numDistinct(s, t)) # 应该输出 5
相关文章:

代码随想录算法训练营Day 54 || 392.判断子序列、115.不同的子序列
392.判断子序列 力扣题目链接(opens new window) 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,&quo…...
和puts())
C 语言 gets()和puts()
C 语言 gets()和puts() gets()和puts()在头文件stdio.h中声明。这两个函数用于字符串的输入/输出操作。 C gets()函数 gets()函数使用户可以输入一些字符,然后按Enter键。 用户输入的所有字符都存储在字符数组中。 空字符将添加到数组以使其成为字符串。 gets()允…...

核—幂零分解
若向量空间 V \mathcal V V存在子空间 X \mathcal X X与 Y \mathcal Y Y,当 X Y V X ∩ Y 0 \mathcal {X\text{}Y\text{}V}\\ \mathcal {X}\cap \mathcal {Y}0 XYVX∩Y0 时称子空间 X \mathcal X X与 Y \mathcal Y Y是完备的,其中记为 X ⊕ Y V \ma…...

轻松掌控财务,分析账户花销,明细记录支出情况
随着科技的发展,我们的生活变得越来越智能化。然而,对于许多忙碌的现代人来说,管理财务可能是一件令人头疼的事情。复杂的账单、花销、收入,这些可能会让你感到无从下手。但现在,我们有一个全新的解决方案——一款全新…...

竞赛 题目:基于机器视觉opencv的手势检测 手势识别 算法 - 深度学习 卷积神经网络 opencv python
文章目录 1 简介2 传统机器视觉的手势检测2.1 轮廓检测法2.2 算法结果2.3 整体代码实现2.3.1 算法流程 3 深度学习方法做手势识别3.1 经典的卷积神经网络3.2 YOLO系列3.3 SSD3.4 实现步骤3.4.1 数据集3.4.2 图像预处理3.4.3 构建卷积神经网络结构3.4.4 实验训练过程及结果 3.5 …...

11. Spring源码篇之实例化前的后置处理器
简介 spring在创建Bean的过程中,提供了很多个生命周期,实例化前就是比较早的一个生命周期,顾名思义就是在Bean被实例化之前的处理,这个时候还没实例化,只能拿到该Bean的Class对象,如果在这个时候直接返回一…...

Python-Python高阶技巧:HTTP协议、静态Web服务器程序开发、循环接收客户端的连接请求
版本说明 当前版本号[20231114]。 版本修改说明20231114初版 目录 文章目录 版本说明目录HTTP协议1、网址1.1 网址的概念1.2 URL的组成1.3 知识要点 2、HTTP协议的介绍2.1 HTTP协议的概念及作用2.2 HTTP协议的概念及作用2.3 浏览器访问Web服务器的过程 3、HTTP请求报文3.1 H…...

P1304 哥德巴赫猜想
题目描述 输入一个偶数 N,验证 4∼N 所有偶数是否符合哥德巴赫猜想:任一大于 22 的偶数都可写成两个质数之和。如果一个数不止一种分法,则输出第一个加数相比其他分法最小的方案。例如 1010,10=3+7=5+510=3+7=5+5,则 10=5+510=5+5 是错误答案。 输入格式 第一行输入一个…...
)
CSDN每日一题学习训练——Python版(搜索插入位置、最大子序和)
版本说明 当前版本号[20231118]。 版本修改说明20231118初版 目录 文章目录 版本说明目录搜索插入位置题目解题思路代码思路参考代码 最大子序和题目解题思路代码思路参考代码 搜索插入位置 题目 给定一个排序数组和一个目标值,在数组中找到目标值,…...

Java在物联网中的重要性
【点我-这里送书】 本人详解 作者:王文峰,参加过 CSDN 2020年度博客之星,《Java王大师王天师》 公众号:JAVA开发王大师,专注于天道酬勤的 Java 开发问题中国国学、传统文化和代码爱好者的程序人生,期待你的关注和支持!本人外号:神秘小峯 山峯 转载说明:务必注明来源(…...

动态规划解背包问题
题目 题解 def knapsac(W: int, N: int, wt: List[int], val: List[int]) -> int:# 定义状态动作价值函数: dp[i][j],对于前i个物品,当前背包容量为j,最大的可装载价值dp [[0 for j in range(W1)] for i in range(N1)]# 状态动作转移for…...

PCL内置点云类型
PCL内置了许多点云类型供我们使用,下面先介绍PLC内置的点云数据类型 PCL中的点云类型为PointT;至于为什么是PointT类型需要追随到原来的ros开发中去,因为PCL库也是从原来的ROS中剥离出来的;大家都一致的认为点云结构是离散的N维信…...

clickhouse数据结构和常用数据操作
背景, 大数据中查询用mysql时间太长, 使用clickhouse 速度快, 数据写入mysql后同步到clickhouse中 测试1千万数据模糊搜索 mysql 需要30-40秒 clickhouse 约 100ms 一 数据结构和存储引擎 1 查看clickhouse所有数据类型 select * from system.data_type_families; 2 …...
upload-labs关卡9(基于win特性data流绕过)通关思路
文章目录 前言一、靶场需要了解的知识1::$data是什么 二、靶场第九关通关思路1、看源码2、bp抓包修改后缀名3、检查是否成功上传 总结 前言 此文章只用于学习和反思巩固文件上传漏洞知识,禁止用于做非法攻击。注意靶场是可以练习的平台,不能随意去尚未授…...

C++过河卒问题
#include <iostream> #include <cstring> using namespace std;int board[20][20]; // 棋盘 int dp[20][20][20][20]; // 动态规划数组int main() {int x0, y0, x1, y1;cin >> x0 >> y0 >> x1 >> y1; // 输入卒的起点和终点memset(board,…...
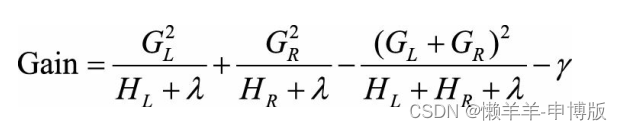
【机器学习12】集成学习
1 集成学习分类 1.1 Boosting 训练基分类器时采用串行的方式, 各个基分类器之间有依赖。每一层在训练的时候, 对前一层基分类器分错的样本, 给予更高的权重。 测试时, 根据各层分类器的结果的加权得到最终结果。 1.2 Bagging …...

nodeJs基础笔记
title: nodeJs基础笔记 date: 2023-11-18 22:33:54 tags: 1. Buffer 1. 概念 Buffer 是一个类似于数组的 对象 ,用于表示固定长度的字节序列。 Buffer 本质是一段内存空间,专门用来处理 二进制数据 。 2. 特点 Buffer 大小固定且无法调整Buffer 性能…...

Skywalking流程分析_9(JDK类库中增强流程)
前言 之前的文章详细介绍了关于非JDK类库的静态方法、构造方法、实例方法的增强拦截流程,本文会详细分析JDK类库中的类是如何被增强拦截的 回到最开始的SkyWalkingAgent#premain try {/** 里面有个重点逻辑 把一些类注入到Boostrap类加载器中 为了解决Bootstrap类…...

矩阵的QR分解
矩阵的QR分解 GramSchmidt 设存在 B { x 1 , x 2 , … , x n } \mathcal{B}\left\{\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{n}\right\} B{x1,x2,…,xn}在施密特正交化过程中 q 1 x 1 ∣ ∣ x 1 ∣ ∣ q_1\frac{x_1}{||x_1||} q1∣∣x1∣∣x1 q k …...

STL总结
STL vector 头文件<vector> 初始化,定义,定义长度,定义长度并且赋值,从数组中获取数据返回元素个数size()判断是否为空empty()返回第一个元素front()返回最后一个数back()删除最后一个数pop_back()插入push_back(x)清空clear()begin()end()使用s…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
