从0开始学习数据结构 C语言实现 1.前篇及二分查找算法
一、前篇
1、什么是数据结构?
数据结构是带有结构特性的数据元素的集合,它研究的是数据的逻辑结构和数据的物理结构以及它们之间的相互关系
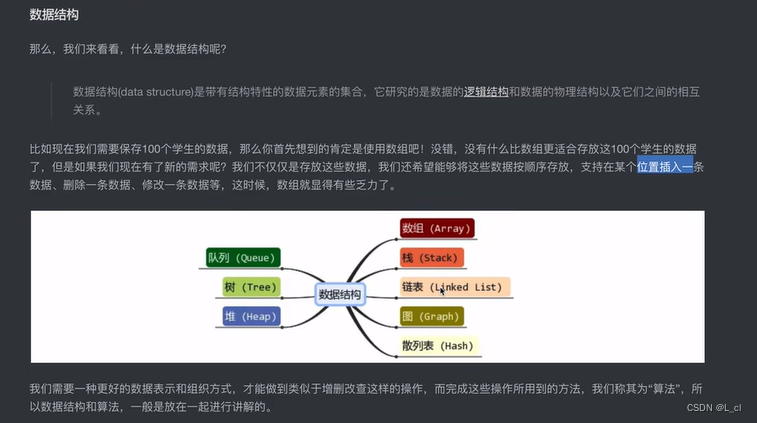
2、时间复杂度与空间复杂度

大O符号是用于描述函数渐进行为的数学符号
常用函数的增长表

阶乘O(n!) > 指数阶(2^n) > 立方阶O(n^3) > 平方阶O(n^2) > 线性对数阶O(nlog2n) > 线性阶O(n) > 对数阶O(log2n) > 常数阶O(1)
从立方阶开始,时间复杂度较大
二、二分查找
在有序数组中查找一个值,如果找到了则返回下标,如果没找到则返回-1
方法一:遍历数组进行查找
时间复杂度:O(n)
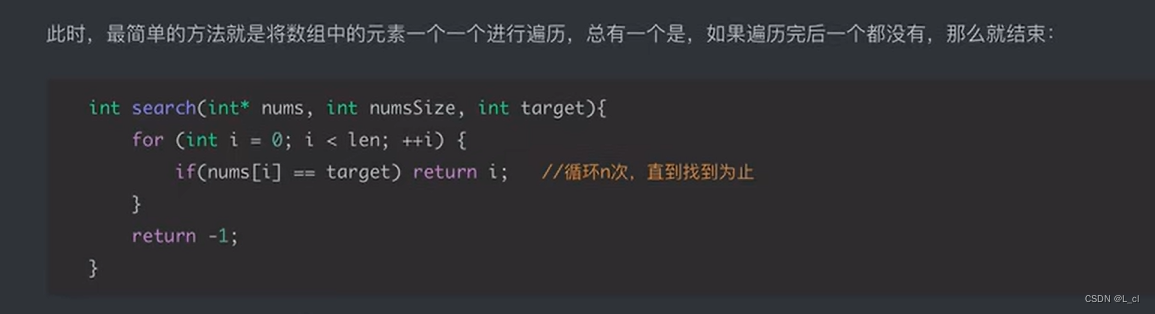
//1.遍历算法在数组中查找一个元素
//方法体
int search(int* arr, int length, int target) {for (int i = 0; i < length; i++) {if (arr[i] == target) {return i;}}
}方法二:减小循环次数进行遍历查找
时间复杂度小于O(n)
因为题目里声明是有序数组,所以当数组中的值比查找的值大时,可以直接break跳出循环,减少循环次数

//2.减小循环次数进行遍历查找
//方法体
int search2(int* arr, int length, int target) {for (int i = 0; i < length; i++) {if (arr[i] == target) {return i;}if (arr[i] > target) {break;}}return -1;
}方法三;二分查找
二分思想就是将一个 有序数组 不断进行平分,直到找到为止,不断平分除以二,降低时间复杂度
时间复杂度:O(og2n)


//3.二分查找
//方法体
int binarySearch(int* arr, int target, int left, int right) {if (left > right) {return -1;}int mid = (left + right) / 2;if (arr[mid] == target) {return mid;}if (arr[mid] > target) {mid = binarySearch(arr, target, left, mid - 1);return mid;}else {mid = binarySearch(arr, target, mid + 1, right);return mid;}
}int search3(int* arr, int length, int target) {return binarySearch(arr, target, 0, length - 1);
}相关文章:

从0开始学习数据结构 C语言实现 1.前篇及二分查找算法
一、前篇 1、什么是数据结构? 数据结构是带有结构特性的数据元素的集合,它研究的是数据的逻辑结构和数据的物理结构以及它们之间的相互关系 2、时间复杂度与空间复杂度 大O符号是用于描述函数渐进行为的数学符号 常用函数的增长表 阶乘O(n!) > 指数…...
VSCode 使用CMakePreset找不到cl.exe编译器的问题
在用vscode开发c项目的时候,使用预先配置的CMakePresets.json可以把一些特定的cmake选项固定下来,在配置时直接使用 "cmake --config --preset presetname"就可以进行配置,免去在命令行输入过多的配置参数。 但是在vscode中&#…...
【Linux系统化学习】进程的状态 | 僵尸进程 | 孤儿进程
个人主页点击直达:小白不是程序媛 Linux专栏:Linux系统化学习 目录 操作系统进程的状态 运行状态 阻塞状态 进程阻塞的现象 挂起阻塞状态 Linux进程状态 Linux内核源代码怎么说 R(running状态)运行状态 S(sl…...
深信服AC流量管理技术
拓扑图 一.保证通道针对修仙部,访问网站,邮件,DNS,IM,办工 OA,微博论坛网上银行等常见应用保证带宽最低 50%,最高 100% 1. 先新建线路带宽 2.新增流量管理通道(保证关键应用&#x…...

二元关系及关系代数中的象集、除运算
二元关系及关系代数中的象集、除运算 数学上,二元关系用于讨论两个数学对象的联系。诸如算术中的「大于」及「等于」,几何学中的"相似",或集合论中的"为...之元素"或"为...之子集"。二元关系有时会简称关系&a…...

[PHP]关联和操作MySQL数据库然后将数据库部署到ECS
在Mac电脑上使用VS Code进行PHP开发并关联操作MySQL数据库,然后将数据库部署到ECS。 1.安装PHP和MySQL 确保你的Mac上已经安装了PHP和MySQL。你可以使用Homebrew来安装它们: $ brew install php $ brew install mysql 安装mysql完成后记住这一句: …...

23.11.19日总结
经过昨天的中期答辩,其实可以看出来项目进度太慢了,现在是第十周,预计第十四周是终级答辩,在这段时间要把项目写完。 前端要加上一个未登录的拦截器,后端加上全局的异常处理。对于饿了么项目的商品建表,之前…...

系列一、JVM概述
一、概述 1.1、Java发展中的重大事件 1.2、虚拟机 vs Java虚拟机 1.2.1、虚拟机 1.2.2、Java虚拟机 1.2.3、Java虚拟机的作用 Java虚拟机是二进制字节码的运行环境,负责装载字节码到其内部,解释/编译为对应平台上的机器指令指令。每一条Java指令&#…...

milvus数据管理-压缩数据
Milvus 默认支持自动数据压缩。您可以 配置 Milvus 以启用或禁用 压缩 和自动压缩。 如果自动压缩被禁用,您仍然可以手动压缩数据。 1.手动压缩数据 压缩请求是异步处理的,因为它们通常需要花费很长时间。 from pymilvus import Collection collection…...

SpringBoot项目连接linux服务器数据库两种解决方法(linux直接开放端口访问本机通过SSH协议访问,以mysql为例)
最近找个springboot脚手架重新熟悉一下springboot相关框架的东西,结果发现好像项目还不能直接像数据库GUI工具一样填几个SSH参数就可以了,于是就给他再整一下看看如何解决 linux开放3306(可修改)端口直接访问 此方法较为方便&am…...

【Rust】快速教程——闭包与生命周期
前言 你怎么向天生的瞎子说清颜色?怎么用手势向天生的聋子描述声音? 鲜花就在眼前,雷鸣就在头顶,对他们来说却都毫无意义 眼睛看不到,鼻子可以嗅闻花香,耳朵听不见,手指可以触碰窗纸的震动。 犯…...
redis高级案列case
案列一 双写一致性 案例二 双锁策略 package com.redis.redis01.service;import com.redis.redis01.bean.RedisBs; import com.redis.redis01.mapper.RedisBsMapper; import lombok.extern.slf4j.Slf4j; import org.springframework.beans.factory.annotation.Autowired; imp…...

Vue3+Vite实现工程化,attribute属性渲染v-bind指令
想要渲染一个元素的attribute,应该使用v-bind指令 由于插值表达式不能直接放在标签的属性中,所有要渲染元素的属性就应该使用v-bindv-bind可以用于渲染任何元素的属性,语法为 v-bind:属性名数据名,可以简写为 :属性名数据名 <…...
下一代搜索引擎会什么?
现在是北京时间2023年11月18日。聊一聊搜索。 说到搜索,大家首先想到的肯定是谷歌,百度。我把这些定义成上一个时代的搜索引擎。ChatGPT已经火热了有一年的时间了,大家都认为Ai搜索是下一代的搜索。但是AI搜索,需要的是很大算力&a…...

WPF中如何在MVVM模式下关闭窗口
完全来源于十月的寒流,感谢大佬讲解 使用Behaviors <Window x:Class"Test_03.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:b"http://schemas.microsoft.com/xaml/behaviors"xmlns:x&quo…...
【数据结构&C++】二叉平衡搜索树-AVL树(25)
前言 大家好吖,欢迎来到 YY 滴C系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 主要内容含: 欢迎订阅 YY滴C专栏!更多干货持续更新!以下是传送门! 目录 一.AVL树的概念二.AVL树节点的定义(代码…...

Python算法——树的最大深度和最小深度
Python中的树的最大深度和最小深度算法详解 树的最大深度和最小深度是树结构中的两个关键指标,它们分别表示树的从根节点到最深叶子节点的最大路径长度和最小路径长度。在本文中,我们将深入讨论如何计算树的最大深度和最小深度,并提供Python…...

46.全排列-py
46.全排列 class Solution(object):def permute(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""# 结果数组0ans[]nlen(nums)# 判断是否使用state_[False]*n# 临时状态数组dp_[]def dfs (index):# 终止条件if indexn:ans.appe…...
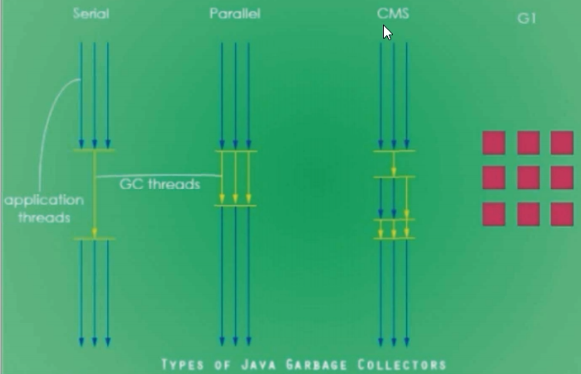
系列三、GC垃圾回收算法和垃圾收集器的关系?分别是什么请你谈谈
一、关系 GC算法(引用计数法、复制算法、标记清除算法、标记整理算法)是方法论,垃圾收集器是算法的落地实现。 二、4种主要垃圾收集器 4.1、串行垃圾收集器(Serial) 它为单线程环境设计,并且只使用一个线程…...
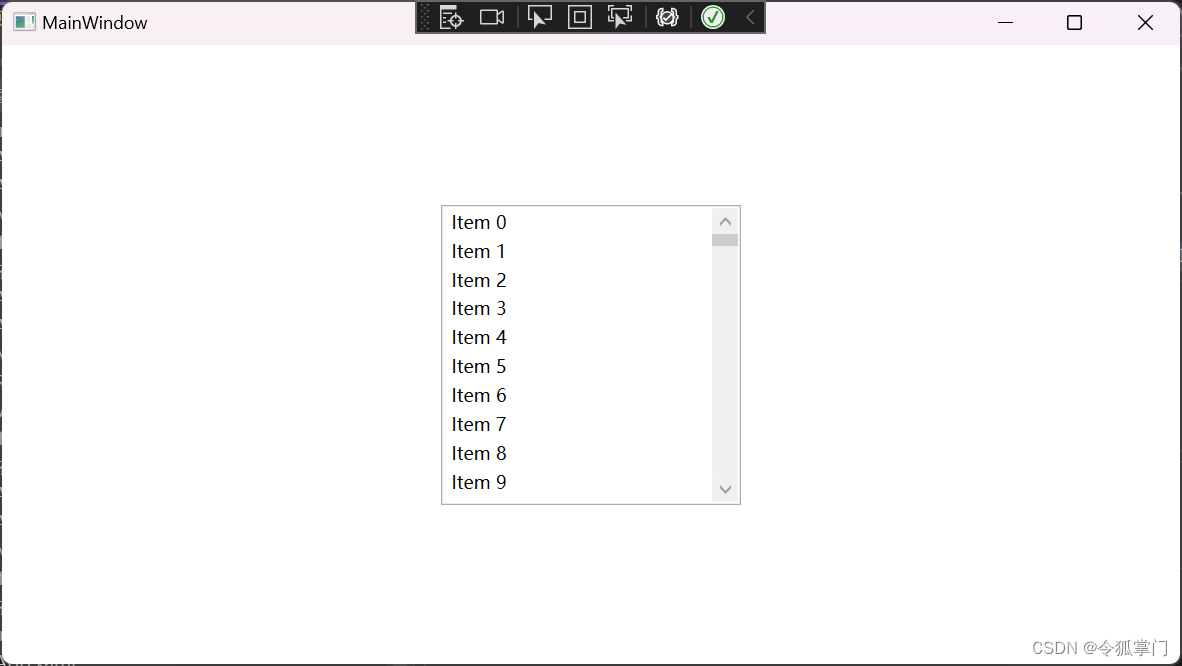
WPF中的虚拟化是什么
WPF(Windows Presentation Foundation)中的虚拟化是一种性能优化技术,它主要用于提高大量数据展示的效率。在WPF中,如果你有一个包含大量项的ItemsControl(例如ListBox、ListView或DataGrid等),…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
