牛掰的dd命令,cpi0配合find备份(不会主动备份),od查看
dd if=设备1或文件 of=设备2或文件 block=nsize count=n 还原就是把设备1,2调过来
这里想到dump的还原是命令restore,想起来就写一下,省的总忘记
可以针对整块磁盘进行复制,对于新创建的分区,也不用格式化,可以直接把数据备份过来
很牛的一个命令,针对备份文件,大概和cp命令差不多,不过针对磁盘,会将磁盘super block
boot sector meta date 全部,对是全部复制过来,所有针对新创建的分区,不用格式化也可以使用。
cpio可备份的更多,不过需要配合其他命令才可以,如find
find /etc | cpio -ocvb > etc.cpio
管道和数据流定向,将etc目录备份etc.cpio
还原 cpio -icvdu < etc.cpio
od查看文件命令
这里为啥要介绍这个命令呢,因为系统里面本身就有cpio文件,还原后想看下里面内容,普通的查看命令提示这是一个binary文件,后来查看之前的命令,找到可以通过od查看,当复习了,想到哪里写到哪里。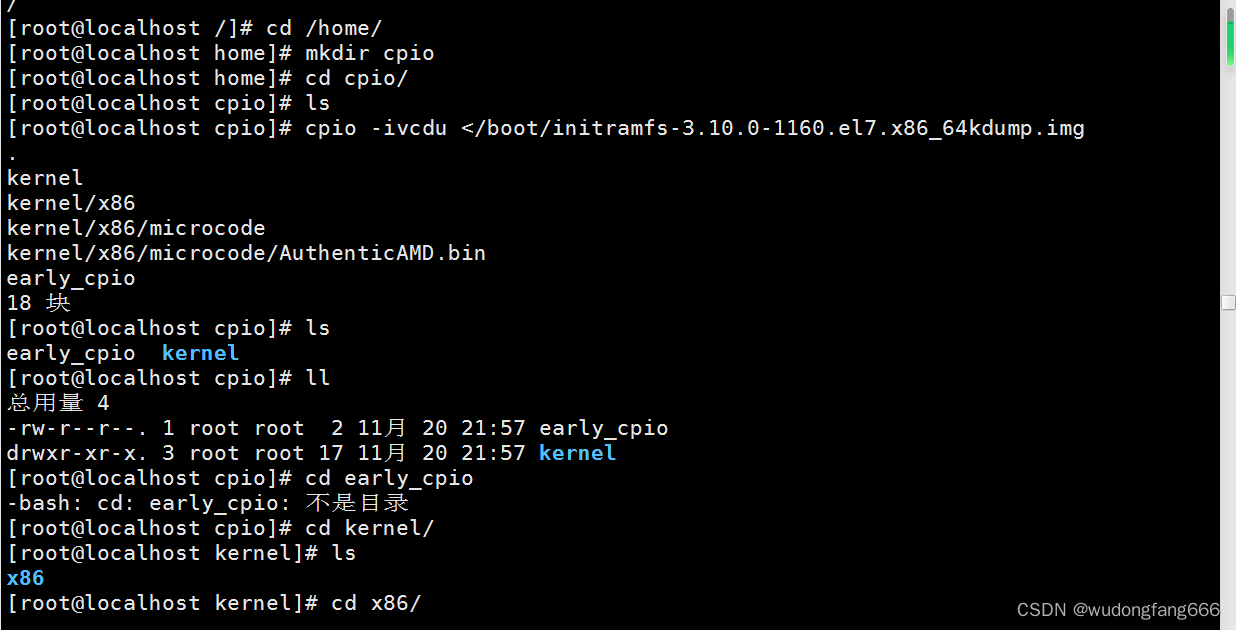
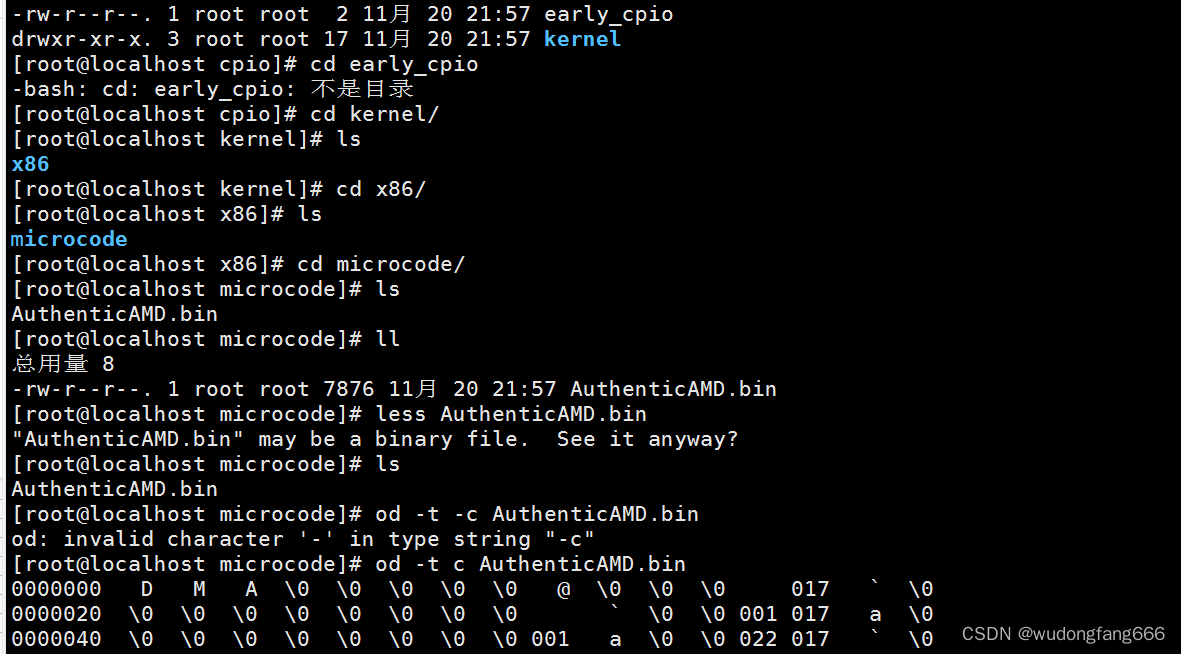
不用od查看的话都是乱码,用od选择字符查看就是如上图一样,虽然也看不懂,但是复习了od命令。学习一遍后就是要联动前后的知识点。
相关文章:

牛掰的dd命令,cpi0配合find备份(不会主动备份),od查看
dd if设备1或文件 of设备2或文件 blocknsize countn 还原就是把设备1,2调过来 这里想到dump的还原是命令restore,想起来就写一下,省的总忘记 可以针对整块磁盘进行复制,对于新创建的分区,也不用格式化,可以直接…...

pip list 和 conda list的区别
PS : 网上说conda activate了之后就可以随意pip了 可以conda和pip混用 但是安全起见还是尽量用pip 这样就算activate了,进入base虚拟环境了 conda与pip的区别 来源 Conda和pip通常被认为几乎完全相同。虽然这两个工具的某些功能重叠,但它们设计用于不…...
多目标应用:基于多目标灰狼优化算法MOGWO求解微电网多目标优化调度(MATLAB代码)
一、微网系统运行优化模型 微电网优化模型介绍: 微电网多目标优化调度模型简介_IT猿手的博客-CSDN博客 二、多目标灰狼优化算法MOGWO 多目标灰狼优化算法MOGWO简介: 三、多目标灰狼优化算法MOGWO求解微电网多目标优化调度 (1)…...
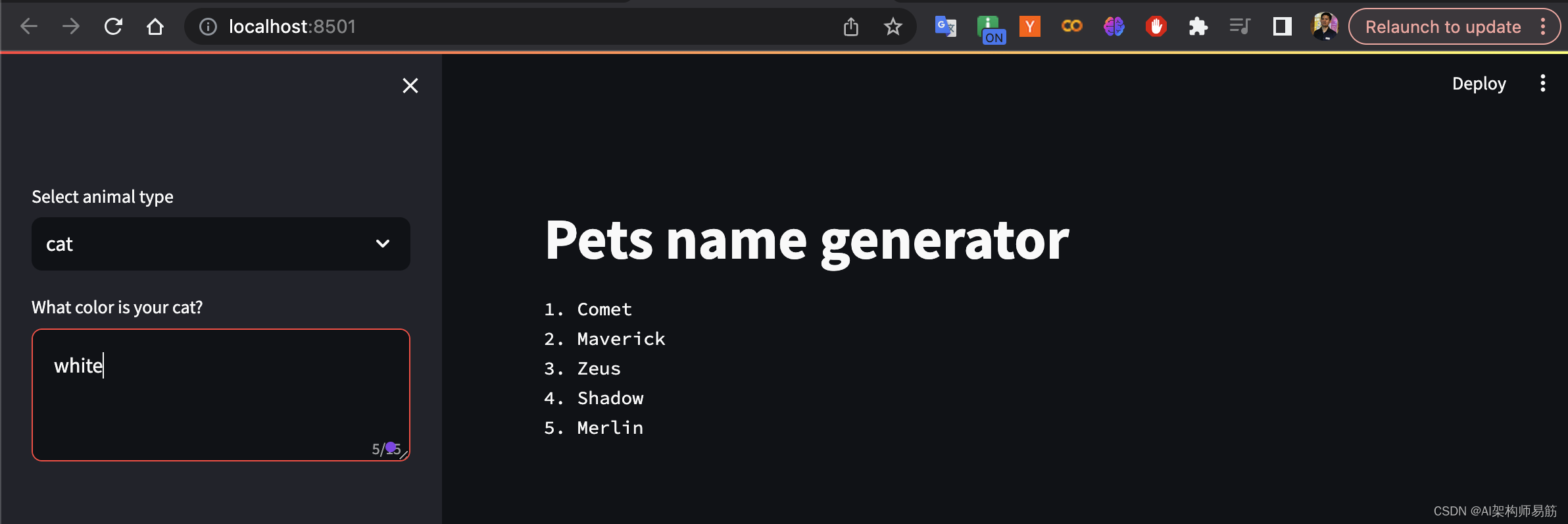
LangChain 2模块化prompt template并用streamlit生成网站 实现给动物取名字
上一节实现了 LangChain 实现给动物取名字, 实际上每次给不同的动物取名字,还得修改源代码,这周就用模块化template来实现。 1. 添加promptTemplate from langchain.llms import OpenAI # 导入Langchain库中的OpenAI模块 from langchain.p…...

linux nas
挂载到本地 mkdir -p /mnt/mountnasdir mount -t nfs 192.168.62:/cnas_id10086_vol10010_dev/ /mnt/mountnasdir...

控制您的音乐、视频等媒体内容
跨多个 Chrome 标签页播放音乐或声音 在计算机上打开 Chrome 。在标签页中播放音乐、视频或其他任何有声内容。您可以停留在该标签页上,也可以转到别处。要控制声音,请在右上角点击“媒体控件”图标 。您可暂停播放、转到下一首歌曲/下一个视频…...
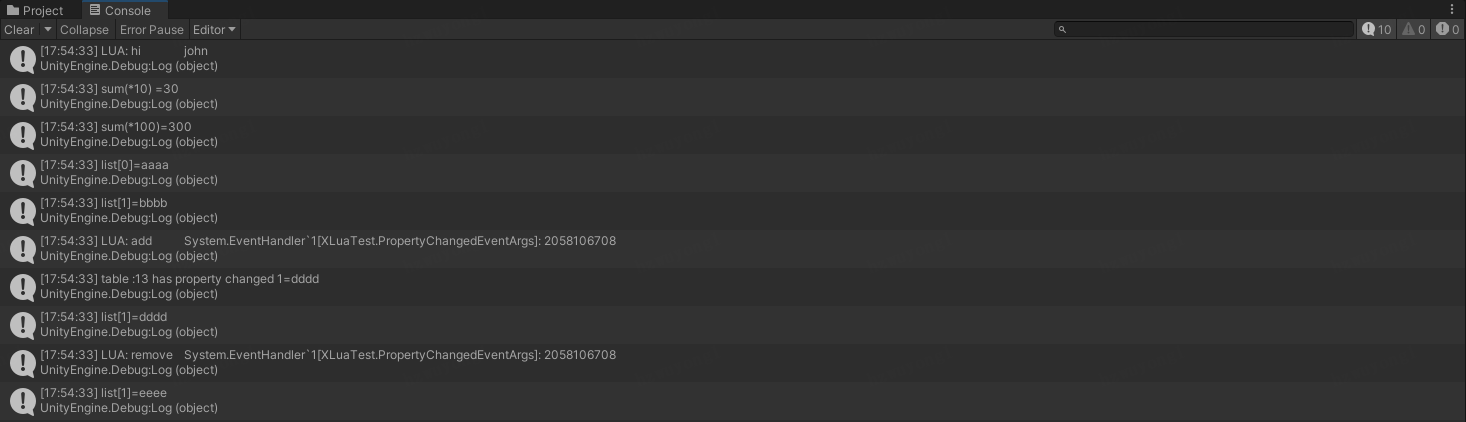
xlua源码分析(三)C#访问lua的映射
xlua源码分析(三)C#访问lua的映射 上一节我们主要分析了lua call C#的无wrap实现。同时我们在第一节里提到过,C#使用LuaTable类持有lua层的table,以及使用Action委托持有lua层的function。而在xlua的官方文档中,推荐使…...

2023 极术通讯-汽车“新四化”路上,需要一片安全山海
导读:极术社区推出极术通讯,引入行业媒体和技术社区、咨询机构优质内容,定期分享产业技术趋势与市场应用热点。 芯方向 【Armv9】-动态TrustZone技术的介绍 动态 TrustZone 是提供多租户安全媒体 pipeline 的绝佳工具。完全不受操作系统、虚…...

Spring Boot接口设计规范
接口参数处理及统一结果响应 1、接口参数处理 1、普通参数接收 这种参数接收方式是比较常见的,由于是GET请求方式,所以在传参时直接在路径后拼接参数和参数值即可。 例如:localhost:8080/api/product/list?key1value1&key2value2 /…...

美创科技与南京大数据安全技术有限公司达成战略合作
近日,美创科技与南京大数据安全技术有限公司正式签署战略合作协议,优势力量共享、共拓共创共赢。 美创科技CEO柳遵梁、副总裁罗亮亮、副总裁王利强,南京大数据安全技术有限公司总经理潘杰、市场总监刘莉莎、销售总监王皓月、技术总监薛松等出…...

2.4路由日志管理
2.4路由/日志管理 一、静态路由和动态路由 路由器在转发数据时,需要现在路由表中查找相应的路由,有三种途径 (1)直连路由:路由器自动添加和自己直连的路由 (2)静态路由:管理员手动…...

归并排序详解:递归实现+非递归实现(图文详解+代码)
文章目录 归并排序1.递归实现2.非递归实现3.海量数据的排序问题 归并排序 时间复杂度:O ( N * logzN ) 每一层都是N,有log2N层空间复杂度:O(N),每个区间都会申请内存,最后申请的数组大小和array大小相同稳定…...
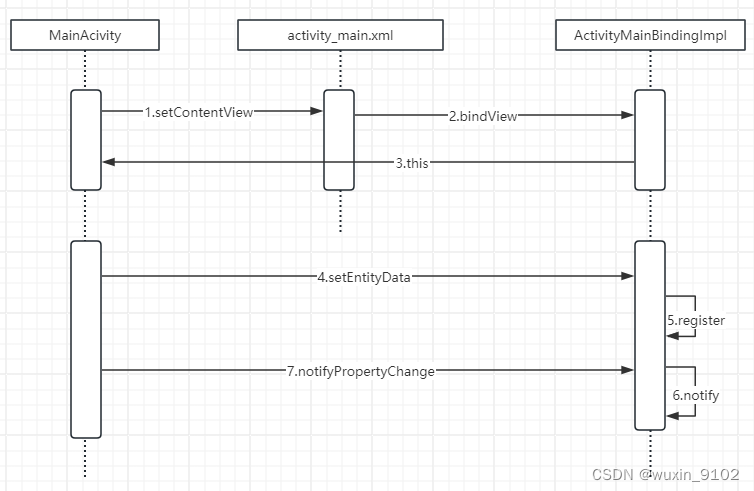
DataBinding原理
1、MainActivity首先使用DataBindingUtil.setContentView设置布局文件activity_main.xml。 2、随后,经过一系列函数调用,ActivityMainBindingImpl对象最终会实例化,并与activity_main.xml进行绑定。 3、实例化后的ActivityMainBindingImpl对象…...
docker更换国内源
docker更换国内源 1、编辑Docker配置文件 在终端中执行以下命令,编辑Docker配置文件: vi /etc/docker/daemon.json2、添加更新源 在打开的配置文件中,添加以下内容: {"registry-mirrors": ["https://hub-mirror…...
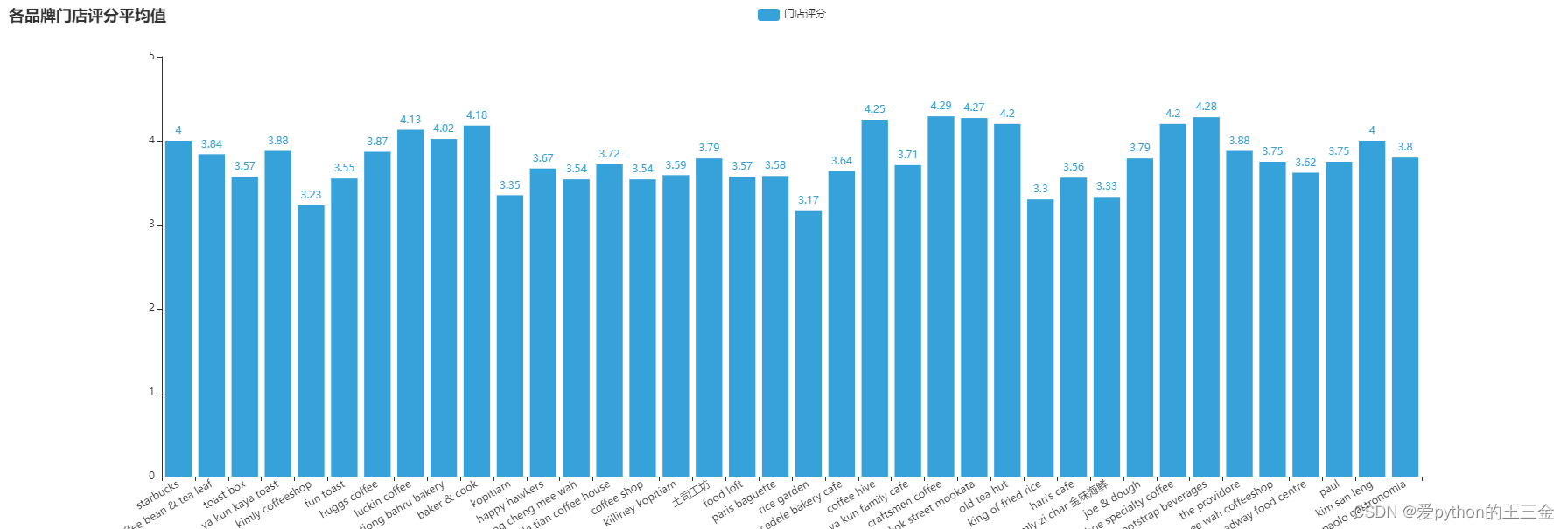
【咖啡品牌分析】Google Maps数据采集咖啡市场数据分析区域分析热度分布分析数据抓取瑞幸星巴克
引言 咖啡作为一种受欢迎的饮品,已经成为我们生活中不可或缺的一部分。随着国内外咖啡品牌的涌入,新加坡咖啡市场愈加多元化和竞争激烈。 本文对新加坡咖啡市场进行了全面的品牌门店数占比分析,聚焦于热门品牌的地理分布、投资价值等。通过…...

【Java】异常处理(一)
🌺个人主页:Dawn黎明开始 🎀系列专栏:Java ⭐每日一句:什么都不做,才会来不及 📢欢迎大家:关注🔍点赞👍评论📝收藏⭐️ 文章目录 📋前…...

【高级程序设计】Week2-4Week3-1 JavaScript
一、Javascript 1. What is JS 定义A scripting language used for client-side web development.作用 an implementation of the ECMAScript standard defines the syntax/characteristics of the language and a basic set of commonly used objects such as Number, Date …...

PHP笔记-->读取JSON数据以及获取读取到的JSON里边的数据
由于我以前是写C#的,现在学一下PHP, 在读取json数据的时候被以前的思维卡住了。 以前用C#读取的时候,是先定义一个数组,将反序列化的json存到数组里面,在从数组里面获取jaon中的“data”数据。 其实PHP的思路也是一样…...

【Spring Boot】如何集成Redis
在pom.xml文件中导入spring data redis的maven坐标。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId></dependency> 在application.yml文件中加入redis相关配置。 spr…...
Elasticsearch备份与还原:使用elasticdump
在数据管理的世界里,备份和还原数据是重中之重的日常工作,特别是对于Elasticsearch这样的强大而复杂的搜索引擎。备份不仅可以用于灾难恢复,还可以在数据迁移、测试或者升级等场景中发挥重要作用。 在本博客中,我们将会重点介绍如…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...
