数字IC前端学习笔记:异步复位,同步释放
相关阅读
数字IC前端![]() https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
异步复位
异步复位是一种常见的复位方式,可以使电路进入一个可知的状态。但是不正确地使用异步复位会导致出现意想不到的错误,复位释放便是其中的一个重要问题,这将在后面进行讨论。
异步复位是通过寄存器的异步复位端实现的,复位端一般是低电平有效,即当复位端为低电平时,寄存器输出被强制复位。
代码风格
下面的代码显示了如何在Verilog代码中说明带有复位的寄存器。注意到复位信号的下降沿事件被加入了敏感列表。其实,异步复位是根据电平生效的,即当复位信号为低时复位。在这里写成下降沿的形式是因为,综合工具要求敏感列表中出现的信号如果有一个是边沿事件,则其他所有事件也必须是边沿敏感的,但这对于仿真工具是可以接受的,甚至仿真工具还可以在敏感列表中存在除了复位沿和时钟沿以外的其他信号事件,这对于综合工具也是不可接受的。
//综合与仿真工具都支持
module FlipFlop(input clk, rst_n, d, output reg q);always@(posedge clk, negedge rst_n)beginif(!rst_n)q <= 1'b0;elseq <= d;end
endmodule//综合工具不支持与仿真工具支持,其实复位效果和上面的代码一致(不要使用它)
module FlipFlop(input clk, rst_n, d, output reg q);always@(posedge clk, rst_n)beginif(!rst_n)q <= 1'b0;elseq <= d;end
endmodule//一个奇怪的例子,但仿真工具确实支持(不要使用它)
module FlipFlop(input clk, rst_n, d, output reg q);always@(posedge clk, rst_n, d)beginif(!rst_n)q <= 1'b0;elseq <= d;end
endmodule异步复位的优势
在进入这个话题前,我们先来看一下上面的第一段代码综合出的电路,如图1所示。可以看到综合工具可以直接从异步复位的Verilog描述中推断出一个带异步复位端的寄存器。
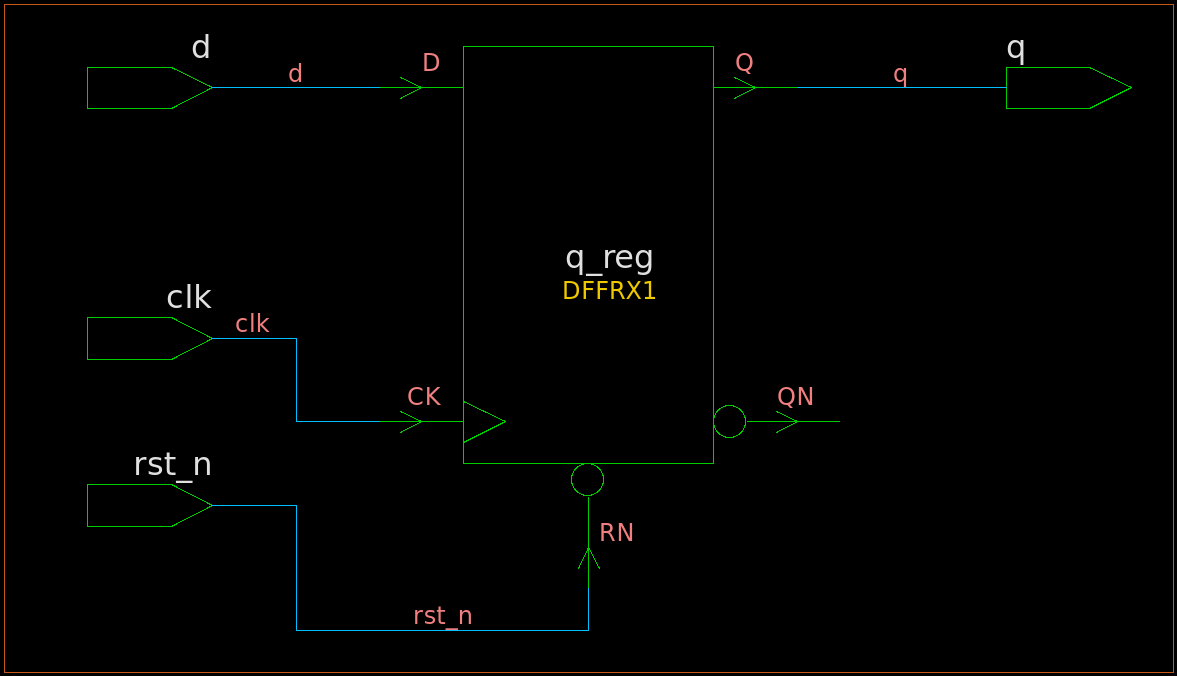
图1 异步复位综合出的寄存器
我们再来看一下同步复位综合出的电路,如图2所示。顺便一提,上面异步复位的代码可以很轻松地改变为同步复位,只要把posedge rst_n从敏感列表中去除即可,如下所示。综合结果显示,异步复位其实就是将异步复位信号当做寄存器输入的一部分,而不是综合出一个有同步复位端的寄存器。对于那些时序上比较紧张的设计,在寄存器前的组合逻辑再插入异步复位的逻辑无法承受,使用异步复位能保证不会给reg2reg的时序路径带来负面影响。异步复位的另一个优点是无需时钟存在便可复位,这使得在时钟尚未启动时复位电路成为了可能。
//同步复位
module FlipFlop(input clk, rst_n, d, output reg q);always@(posedge clk)beginif(!rst_n)q <= 1'b0;elseq <= d;end
endmodule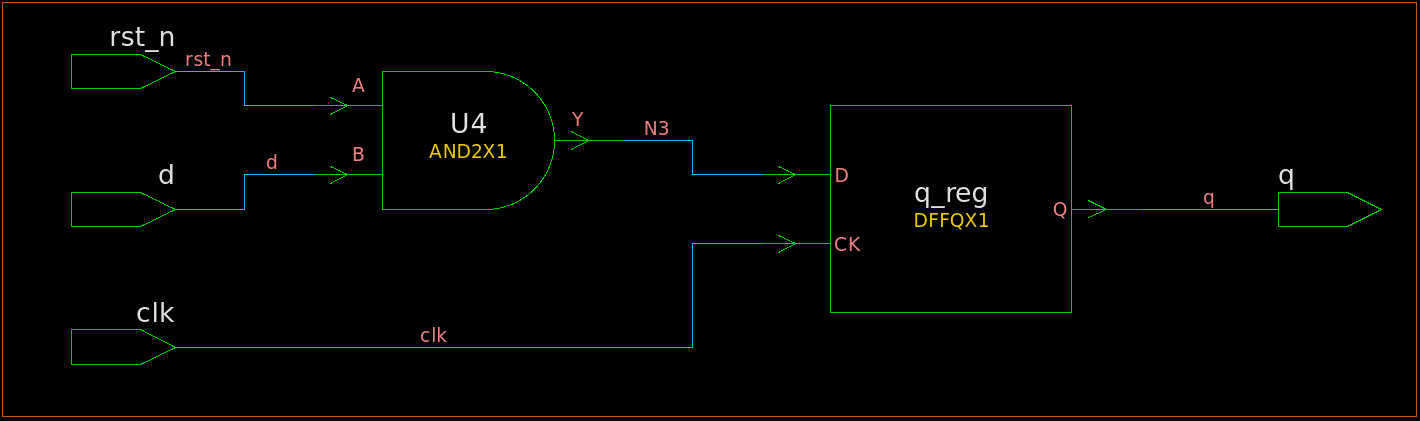
图2 同步复位综合出的寄存器
异步复位的问题
异步复位中也存在一定问题,因为复位信号的使能和释放都是异步的。不正确的复位释放,即复位沿过于接近时钟沿会导致寄存器输出现亚稳态(复位的生效不会导致出现亚稳态,因为复位是强制将输出拉低)。其实同步复位也有相似的问题,因为同步复位信号需要像其他输入信号一样满足建立时间、保持时间的要求,否则会在寄存器输出产生亚稳态。
Removal时间和Recovery时间
与建立时间和保持时间类似,removal时间和recovery时间被用来描述复位信号的时序要求。如图3所示,removal时间指的是复位释放不能过于靠近时钟有效沿的后方,而Recovery指的是复位释放不能过于靠近有效沿的前方。这两种条件都可能造成输出的亚稳态,因为复位相当于内部信号的改变,这种改变过于靠近时钟沿会导致电路逻辑状态不定。
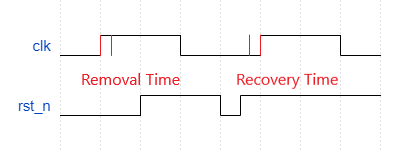
图3 复位信号释放的要求
复位同步器
就像CDC(跨时钟域)问题一样,复位信号的释放同样也可以使用同步器与时钟沿进行同步,这就是“异步复位,同步释放”。
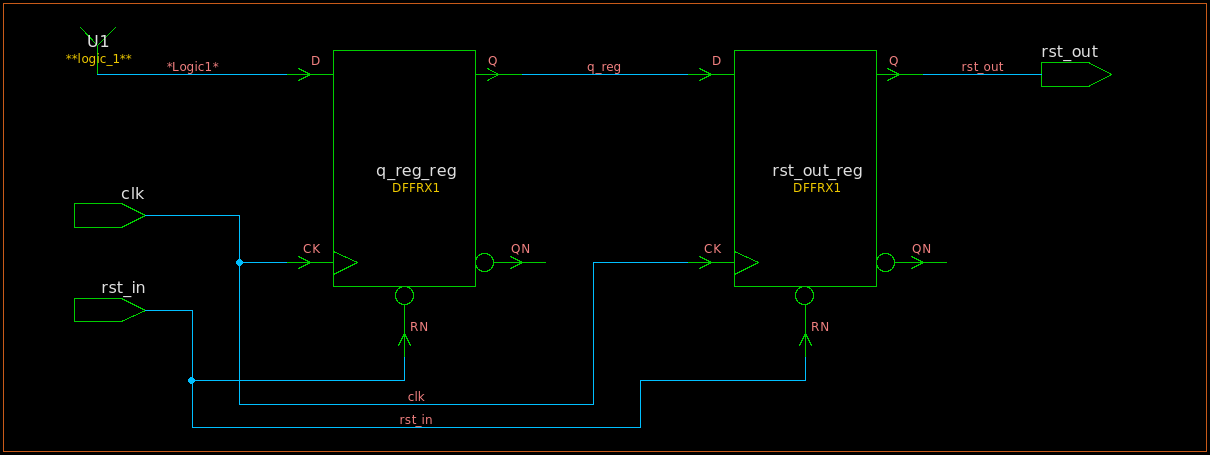
以上结构的Verilog描述如下所示。
module reset_syn(input clk, rst_in, output reg rst_out);reg rst_r;always@(posedge clk, negedge rst_in)beginif(!rst_n){rst_out, rst_r} <= 2'b0;else{rst_out, rst_r} <= {rst_r, 1'b1};end
endmodule在同步了复位释放信号后,第一个寄存器的输出依然可能出现亚稳态,但这个不确定状态在传播到第二个寄存器输入前已经稳定(可能是1,也可能是0),即下一个时钟边沿在第二个寄存器输出不会出现亚稳态,这也意味着同步后复位释放信号会延迟输入的复位释放信号1至2个周期。
甚至为了保险起见还可以使复位再延迟一段时间再释放,这样可以在最大程度上确保复位正常释放,如下所示。
`define count 16'hffff
module reset_syn(input clk, rst_in, output reg rst_out);reg rst_r, rst_cnt, rst_pre;always@(posedge clk, negedge rst_in)beginif(!rst_in){rst_pre, rst_r} <= 2'b0;else{rst_pre, rst_r} <= {rst_r, 1'b1};endalways@(posedge clk, negedge rst_pre)beginif(!rst_pre) rst_cnt <= 0;else if(rst_cnt < `count)rst_cnt = rst_cnt + 1;endalways@(posedge clk, negedge rst_pre)beginif(!rst_pre) rst_out <= 0;else if(rst_cnt == `count)rst_out <= 1'b1;elserst_out <= 1'b0;end endmodule相关文章:

数字IC前端学习笔记:异步复位,同步释放
相关阅读 数字IC前端https://blog.csdn.net/weixin_45791458/category_12173698.html?spm1001.2014.3001.5482 异步复位 异步复位是一种常见的复位方式,可以使电路进入一个可知的状态。但是不正确地使用异步复位会导致出现意想不到的错误,复位释放便是…...

Linux内核移植之网络驱动更改说明一
一. 简介 本文学习 NXP官方Linux内核移植网络驱动的更改。 为了方便后面 Linux驱动的开发调试,所以,必须要把网络驱动调试好。 如果在做 Linux驱动开发时,写了一个 app或驱动,就需要将系统全部文件(即 uboot&#…...

邮件|gitpushgithub报错|Lombok注解
基于 Spring Boot 搭建一个定时发送邮件的项目可以按照以下步骤进行: 创建一个新的 Spring Boot 项目,并添加所需的依赖。在 pom.xml 文件中添加以下依赖项(根据你的需要进行调整): xml org.springframework.boot sp…...

【前端知识】Node——events模块的相关方法
一、events模块的常用方法 // 事件总线 const EventsEmitter require(events);const emitter new EventsEmitter();function HLog(msg){console.log(msg); }// 监听 emitter.on(hlog, HLog);setTimeout(() > {// 触发,打印emitter.emit(hlog, hello emitter!)…...
广州华锐互动VRAR | VR课件内容编辑器解决院校实践教学难题
VR课件内容编辑器由VR制作公司广州华锐互动开发,是一款专为虚拟现实教育领域设计的应用,它能够将传统的教学内容转化为沉浸式的三维体验。通过这款软件,教师可以轻松创建和编辑各种虚拟场景、模型和动画,以更生动、直观的方式展示…...
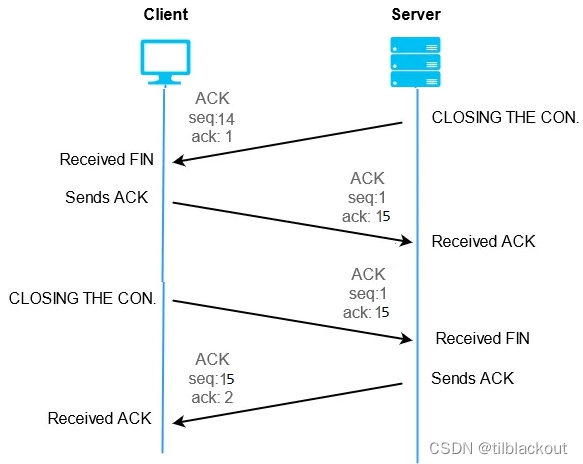
Wireshark抓包:理解TCP三次握手和四次挥手过程
TCP是一种面向连接、端到端可靠的协议,它被设计用于在互联网上传输数据和确保成功传递数据和消息。本节来介绍一下TCP中的三次握手和四次挥手。 文章目录 1 TCP头部格式2 wireshark抓包分析2.1 SEQ和ACK2.2 三次握手2.3 四次挥手 3 程序 1 TCP头部格式 TCP头部占据…...

网络工程师-HCIA网课视频学习
这里是速成的,只积累下,自己未曾学习到的东西。通过书本补充知识点。 视频:hcia17-链路聚合_哔哩哔哩_bilibili hcia16-路由高级特性: hcia17-链路聚合: 由于如果根据视频来学习的话,感觉视频的总结并不…...
【每日刷题——语音信号篇】
思考与练习 练习2.1 语音信号在产生的过程中,以及被感知的过程中,分别要经过人体的哪些器官? 1.产生过程: 肺部空气 → \rightarrow →冲击声带 → \rightarrow →通过声道(可以调节) → \rightarrow →…...

Linux进程通信——IPC、管道、FIFO的引入
进程间的通信——IPC 进程间通信 (IPC,InterProcess Communication) 是指在不同进程之间传播或交换信息。 IPC的方式通常有管道 (包括无名管道和命名管道) 、消息队列、信号量、共享存储、Socket、Streams等。其中 Socket和Streams支持不同主机上的两个进程IPC。 …...
)
数理统计的基本概念(一)
文章目录 总体、样本与统计量总体及其分布样本及其分布统计量统计量概念样本矩顺序统计量及其分布样本中位数与样本极差经验分布函数 参考文献 总体、样本与统计量 总体及其分布 在数理统计中,称所研究的对象的全体为总体,总体中的元素称为个体。若总体…...
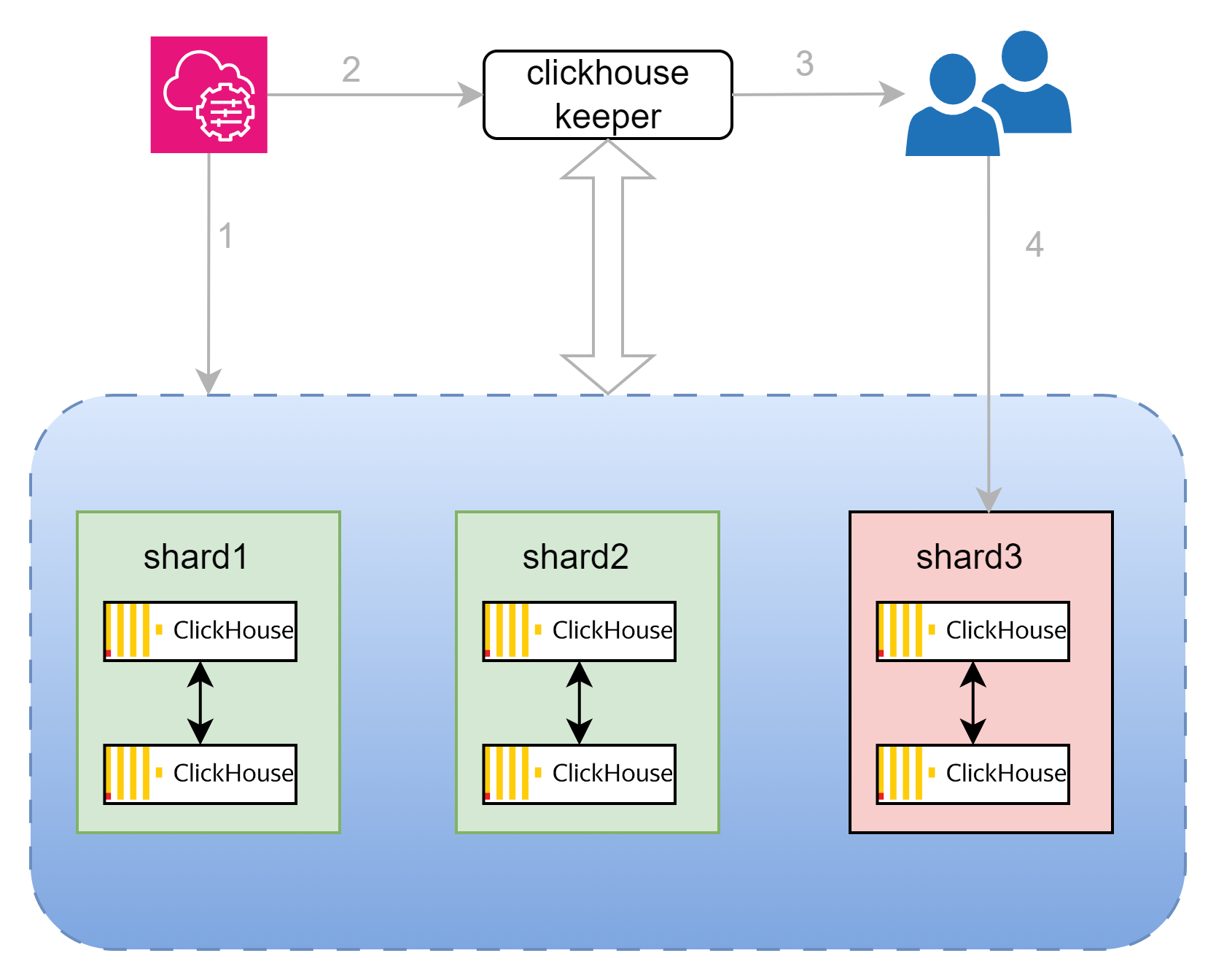
clickhouse分布式之弹性扩缩容的故事
现状 社区不支持喔,以后也不会有了。曾经尝试过,难道是是太难了,无法实现吗?因为他们企业版支持了,可能是利益相关吧,谁知道呢,毕竟开源也要赚钱,谁乐意一直付出没有回报呢。 社区…...
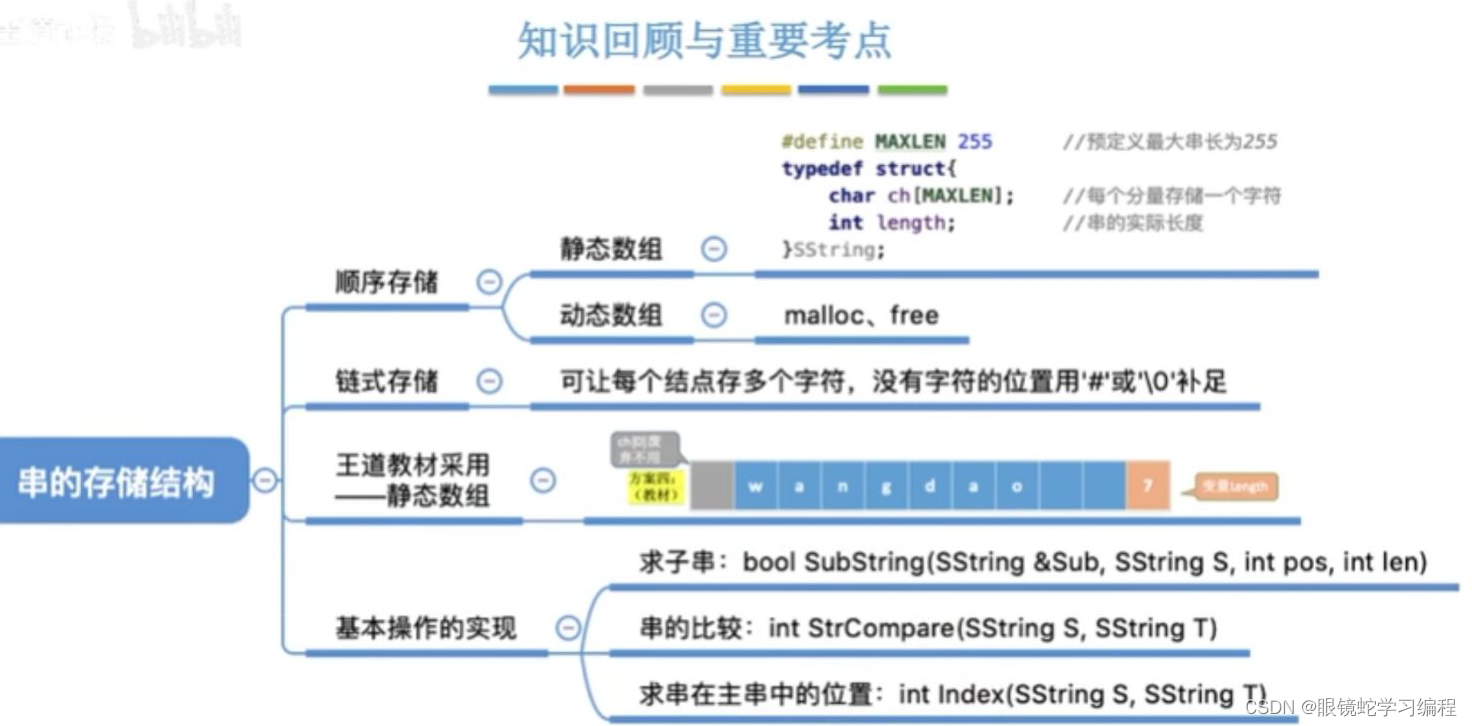
数据结构--串的基本概念
目录 串的基本概念 串的定义 串与线性表对比 串的基本操作 串的比较 字符集编码 乱码问题编辑 总结 串的存储结构 串的顺序存储编辑 串的链式存储 串的基本操作 1、求字串 2、比较 3、定位操作 总结 串的基本概念 串的定义 串与线性表对比 串的…...

音视频流媒体之 IJKPlayer FFmpeg Android 编译
FIJK dockerfile 编译环境 FROM --platformlinux/amd64 ubuntu:18.04RUN apt-get update && apt-get install -y \wget \unzip \git \gcc \g \make \python \yasm \pkg-config \protobuf-compiler \sudoRUN apt-get install -y openjdk-8-jdkENV ANDROID_HOME…...
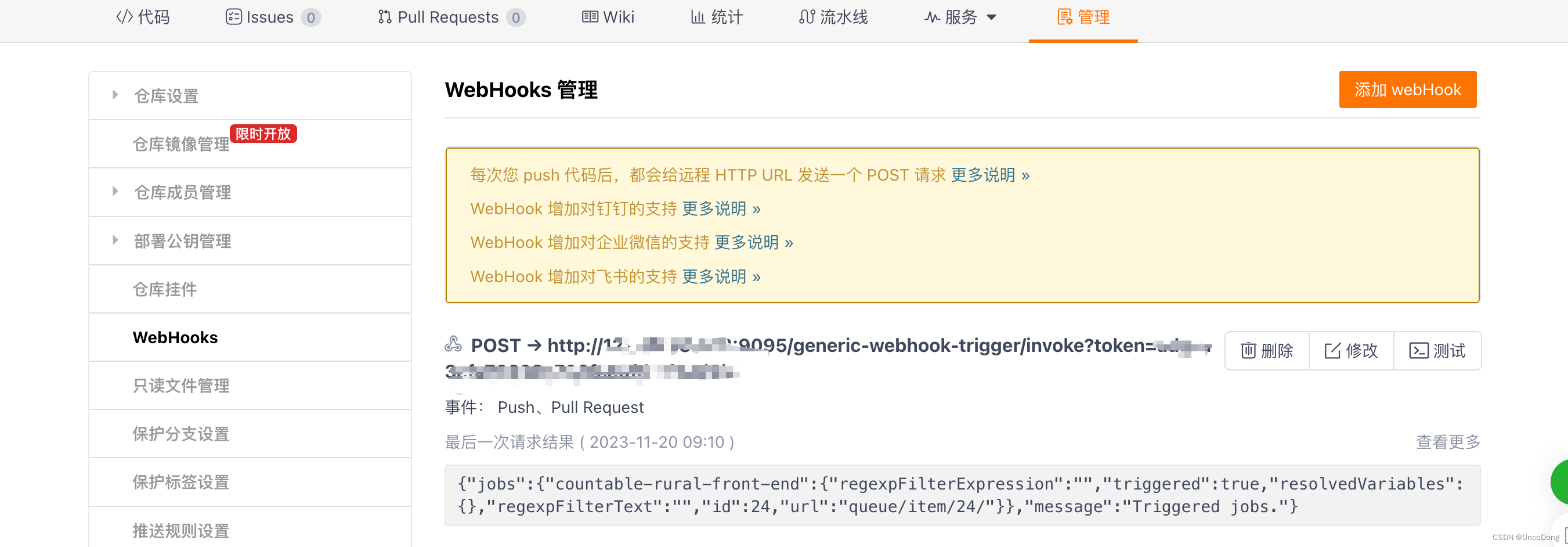
记录一次较为完整的Jenkins发布流程
文章目录 1. Jenkins安装1.1 Jenkins Docker安装1.2 Jenkins apt-get install安装 2. 关联github/gitee服务与webhook2.1 配置ssh2.2 Jenkins关联2.3 WebHook 3. 前后端关联发布 1. Jenkins安装 1.1 Jenkins Docker安装 Docker很好,但是我没有玩明白如何使用Docke…...
Virtual安装centos后,xshell连接centos 测试及遇到的坑
首先来一张官方的图--各种网络模式对应的连接状况: 1. 网络使用Host-Only模式动态分配IP,点确定后,centos 上运行 system restart network ,使用ifconfig查看新的ip,XShell可以直接连上centos, 但是由于使用…...
)
【算法】最优乘车——bfs(stringsteam的实际应用,getline实际应用)
题目 H 城是一个旅游胜地,每年都有成千上万的人前来观光。 为方便游客,巴士公司在各个旅游景点及宾馆,饭店等地都设置了巴士站并开通了一些单程巴士线路。 每条单程巴士线路从某个巴士站出发,依次途经若干个巴士站,…...
『亚马逊云科技产品测评』活动征文|通过lightsail一键搭建Drupal VS 手动部署
『亚马逊云科技产品测评』活动征文|通过lightsail一键搭建Drupal 提示:授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre, 知乎,自媒体平台,第三方开发者媒体等亚…...

使用 VuePress 和 Vercel 打造个人技术博客:实现自动化部署
什么是VuePress? 以下是VuePress官方文档的介绍:VuePress 是一个以 Markdown 为中心的静态网站生成器。你可以使用 Markdown 来书写内容(如文档、博客等),然后 VuePress 会帮助你生成一个静态网站来展示它们。VuePress 诞生的初…...
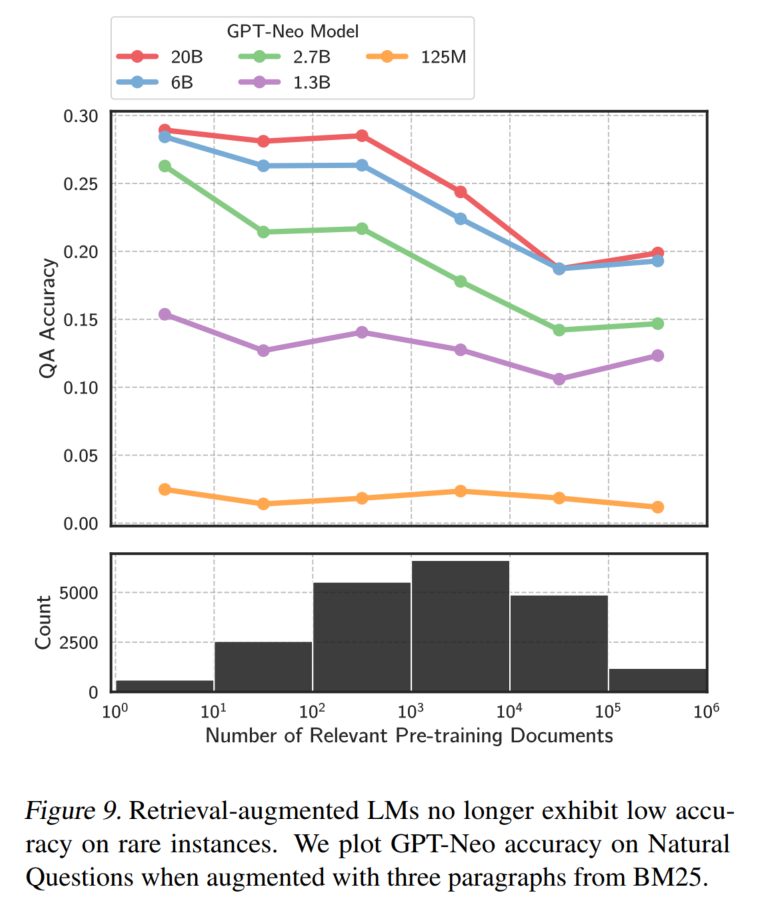
Re50:读论文 Large Language Models Struggle to Learn Long-Tail Knowledge
诸神缄默不语-个人CSDN博文目录 诸神缄默不语的论文阅读笔记和分类 论文名称:Large Language Models Struggle to Learn Long-Tail Knowledge ArXiv网址:https://arxiv.org/abs/2211.08411 官方GitHub项目(代码和实体)…...
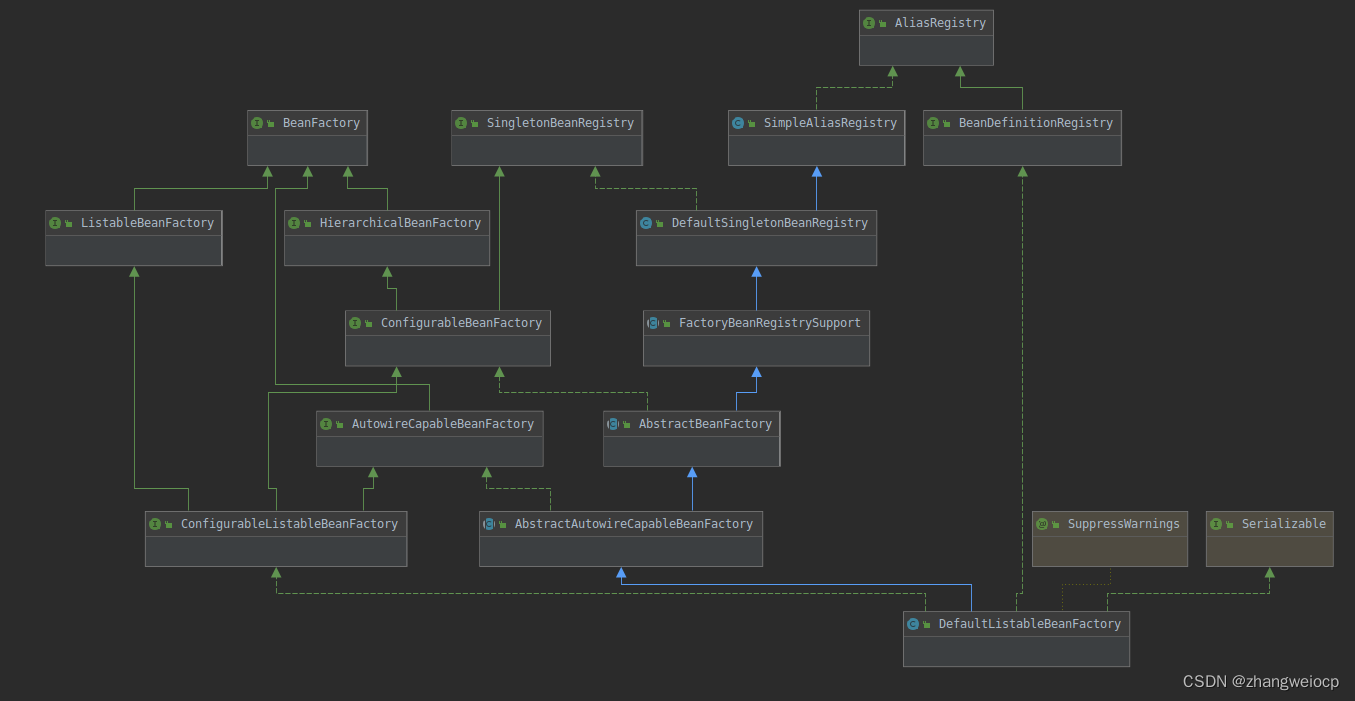
Spring IOC - Bean的生命周期之依赖注入
在Spring启动流程中,创建的factoryBean是DefaultListableBeanFactory,其类图如下所示: 可以看到其直接父类是AbstractAutoireCapableBeanFactory,他主要负责完成Bean的自动装配和创建工作。 具体来说,AbstractAutowire…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
