[数据结构]-红黑树
前言
作者:小蜗牛向前冲
名言:我可以接受失败,但我不能接受放弃
如果觉的博主的文章还不错的话,还请
点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正
目录
一、红黑树的基本知识
1、红黑树的概念
2、性质
二、红黑树的模拟实现
1、节点的定义
2、红黑树的插入
三、红黑树的测试
1、验证的准备工作
2、测试用例
3、完整代码实现
四、AVL树和红黑树的比较
本期学习目标:什么是红黑树,红黑树是怎么实现的,红黑树的测试,红黑树和AVL树的对比
一、红黑树的基本知识
1、红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路 径会比其他路径长出俩倍(最长路径吧会超过最短路径的2倍),因而是接近平衡的。
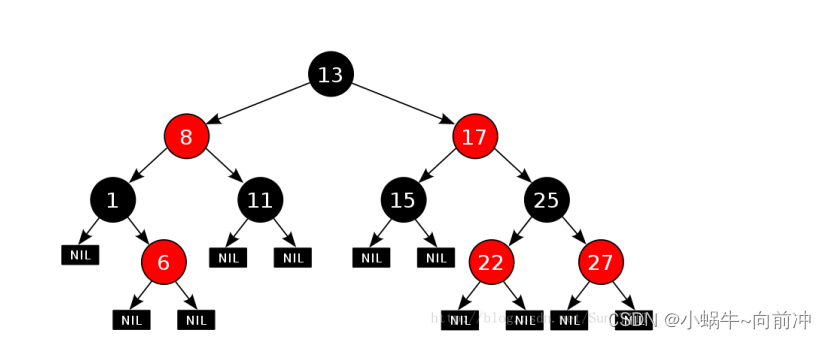
2、性质
- 每个结点不是红色就是黑色。
- 根节点是黑色的 。
- 如果一个节点是红色的,则它的两个孩子结点是黑色的。(没有连续的红节点)
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点 。(每条路径下都包含相同的黑节点)
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)。
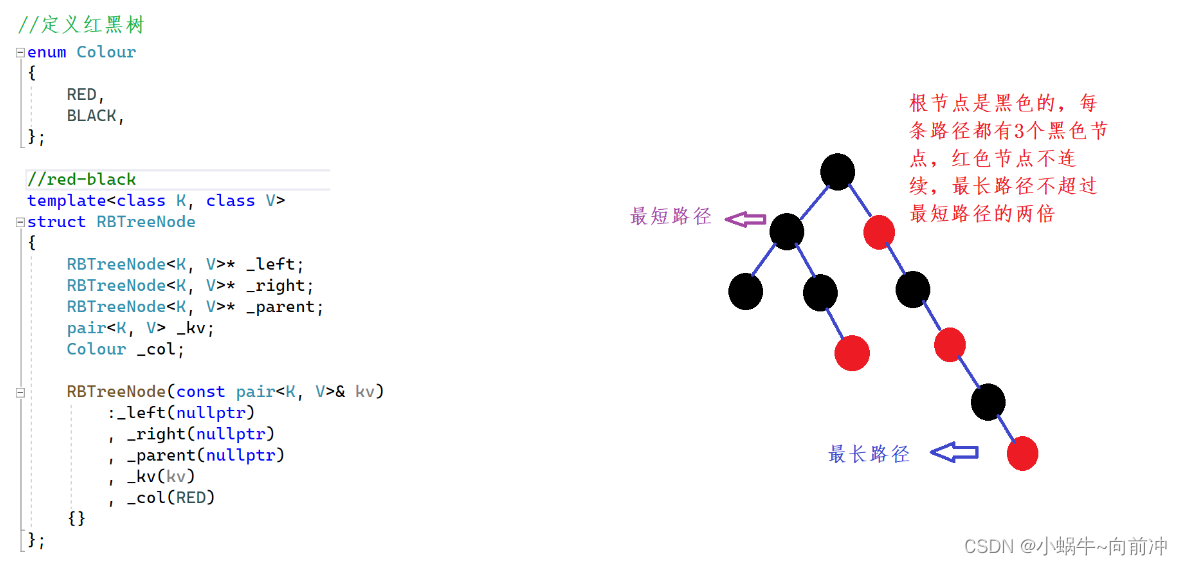 推论:
推论:
- 最短路径:全部由黑节点组成
- 最长路径:一黑一红,红节点数量 == 黑节点数量
这里我们思考一下,红黑树是如何保证:最长路径不超过最短路径的2倍?
- 由推论2可知,对于最长路经,就是一红一黑,而且红节点数量等于黑节点数量,
- 在由推论1可知,最短路径节点数量全为黑。
- 在由性质4可知,每条路径的黑节点数量都相同,这就保证了最长路径不超过2倍的最短路径。
二、红黑树的模拟实现
1、节点的定义
enum Colour
{RED,BLACK,
};template<class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}
};2、红黑树的插入
根据节点的定义,我们上面定义了一个枚举类型了存放显色的类型,RED和BLACK,但是我们在插入节点的时候是定义红色还是黑色呢?我们在上面定义的是红色为什么呢?
这里分类讨论一下:
定义新插入节点为黑色:
就会破坏性质4,导致每天路径的黑色节点数量不同
定义新插入节点为红色:
可能会破坏性质3,导致出现连续的红节点,但是这样也仅仅影响的是一条路径,影响有限。
综上所述:所以我们选择插入节点为红色。
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
1. 按照二叉搜索的树规则插入新节点
2.检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点(p:parent g:grandfather u:uncle)
当p为g的左孩子时,有3种情况需要讨论
情况1:

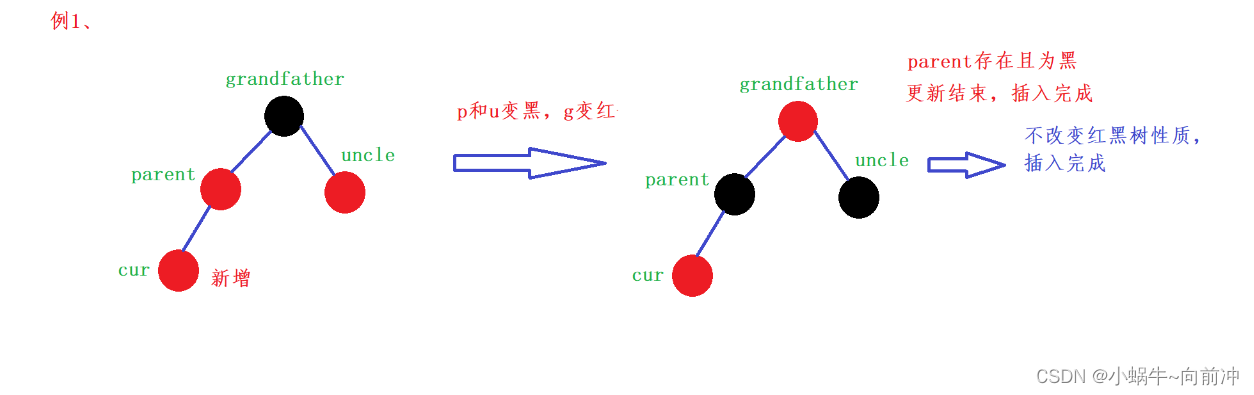
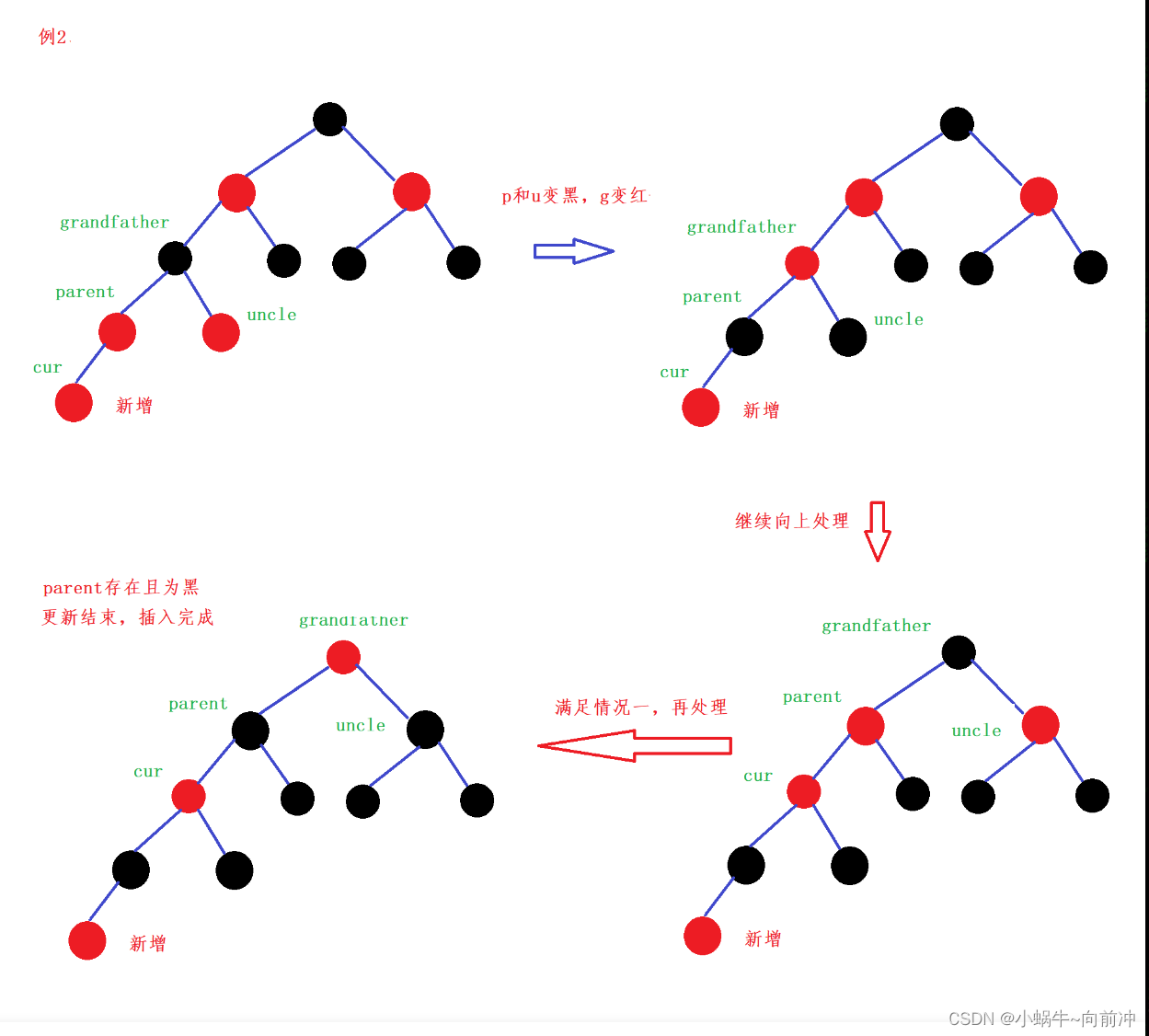
情况2:
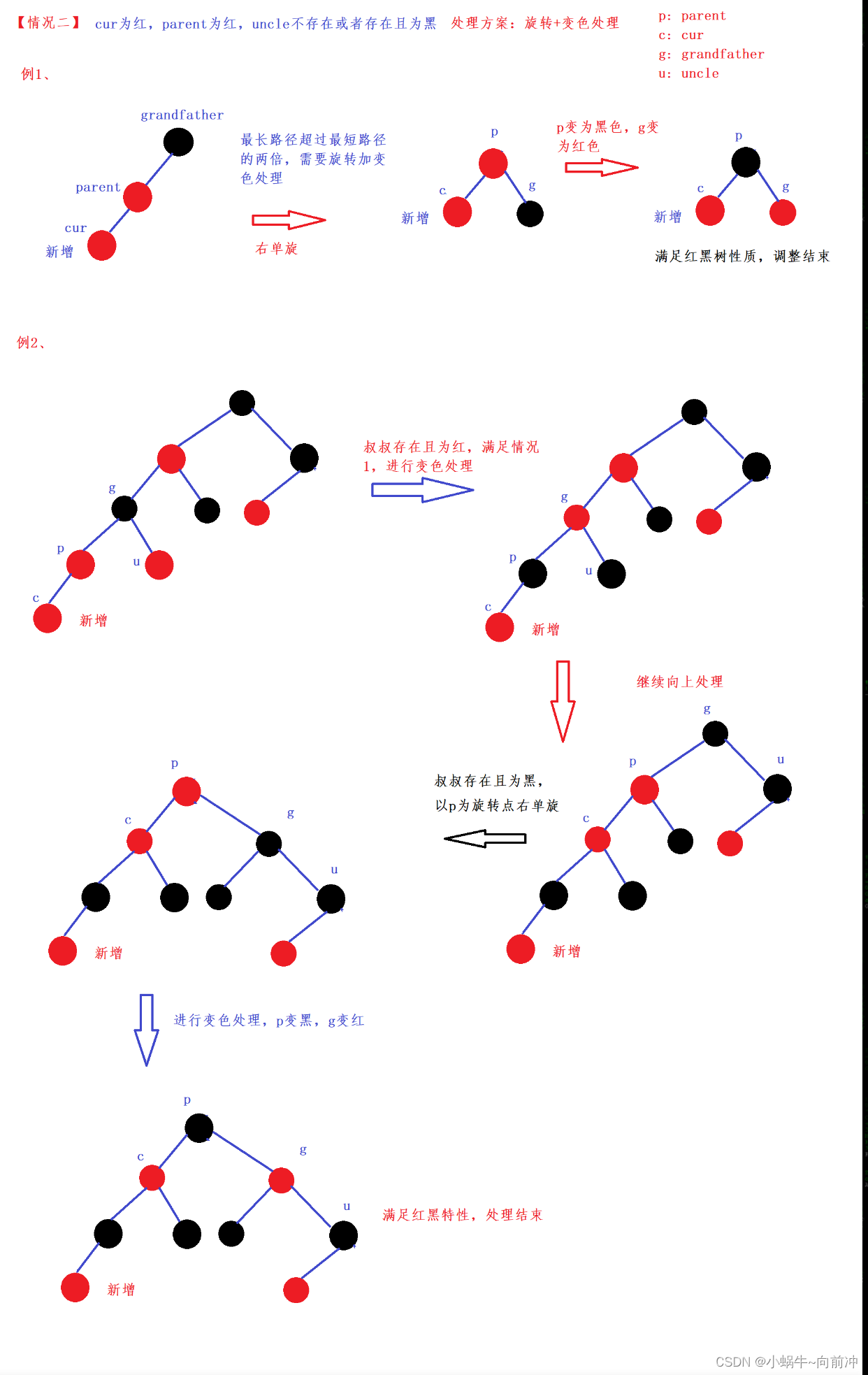
情况3:
 当p为g的右孩子时,也有3种情况需要讨论
当p为g的右孩子时,也有3种情况需要讨论
这里的讨论和上面相似,处理方法也相似:
情况1:

情况2:
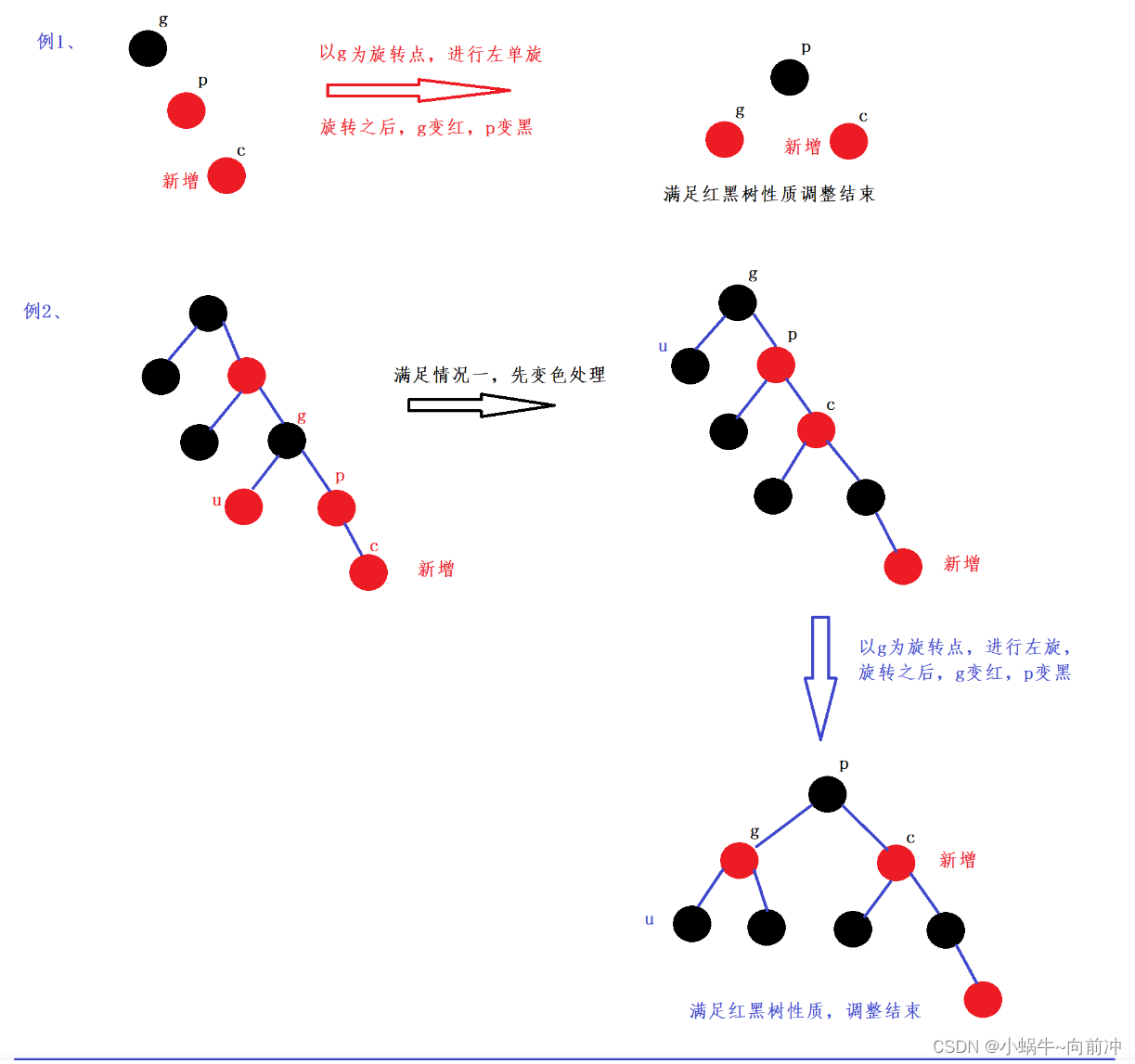
情况3:

代码实现:
bool insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//找到插入位置Node* parent = nullptr;Node* cur = _root;while (cur){//到左子树找if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}//找到了cur = new Node(kv);cur->_col = RED;//默认颜色为红色//链接节点if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//插入后要调整红黑树//如果父亲存在且为红色while (parent && parent->_col == RED){Node* grandparent = parent->_parent;//情况1:cur为红色,p和u都为红色,g为黑色,这里的u是存在的//解决方法:p和n都变黑,g变红,在把cur当做g继续调整if (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;//更新parentparent = cur->_parent;}else//情况2+3 uncle存在且为黑色或者uncle不存在{if (cur == parent->_left){//情况2//解决方法:右单旋,将p变黑,g变红RotateR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}else//情况3:双旋转{RotateL(parent);RotateR(grandparent);grandparent->_col = RED;cur->_col = BLACK;//双旋转后cur变为了根}//这里类比根节点为色,不需要在调整了break;}}else//grandparent->right == parent{//这里也是和上面一样分为三种情况Node* grandparent = parent->_parent;Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;//更新parentparent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandparent);//左单旋转parent->_col = BLACK;grandparent->_col = RED;}else{RotateR(parent);RotateL(grandparent);grandparent->_col = RED;cur->_col = BLACK;//双旋转后cur变为了根}break;}}}//调整完成,把根节点变黑_root->_col = BLACK;return true;
}
//右单旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;Node* grandparent = parent->_parent;//让subLR变为parent的左,parent->_left = subLR;//这里要判断一下subLR不为空if (subLR){subLR->_parent = parent;}//parent变为subL的右subL->_right = parent;parent->_parent = subL;//parent就是为根if (grandparent == nullptr){_root = subL;subL->_parent = grandparent;}else{//parnet是上grandparent的左子树if (grandparent->_left == parent){grandparent->_left = subL;}else{grandparent->_right = subL;}subL->_parent = grandparent;}
}//左单旋
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;Node* ppNode = parent->_parent;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;//parnet为根,要更新根if (ppNode == nullptr){_root = subR;subR->_parent = ppNode;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}
}三、红黑树的测试
1、验证的准备工作
-
检测其是否满足二叉搜索树(中序遍历是否为有序序列)
-
检测其是否满足红黑树的性质
检测方法:
1、根节点是黑色,否则不是红黑树
2、当前节点是红色,去检测父亲节点,父亲节点也是红色,则不是红黑树
3、以最左侧路径的黑色节点为基准,其它路径上的黑色节点与基准不相等,不是红黑树
检验代码:
void Inorder()
{_Inorder(_root);
}void _Inorder(Node* root)
{if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);
}bool Check(Node* root, int blackNum, const int ref)
{if (root == nullptr){//已经递归到最深处进行,本路径的黑节点树和ref数量对比if (blackNum != ref){cout << "违反规则:本条路径的黑色节点的数量跟最左路径不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则:出现连续红色节点" << endl;return false;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);
}bool IsBalance()
{if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}//求出最左路节点有多少个黑节点int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK){++ref;}left = left->_left;}return Check(_root, 0, ref);
}2、测试用例
这里我们借用上面AVL树的测试用例即可
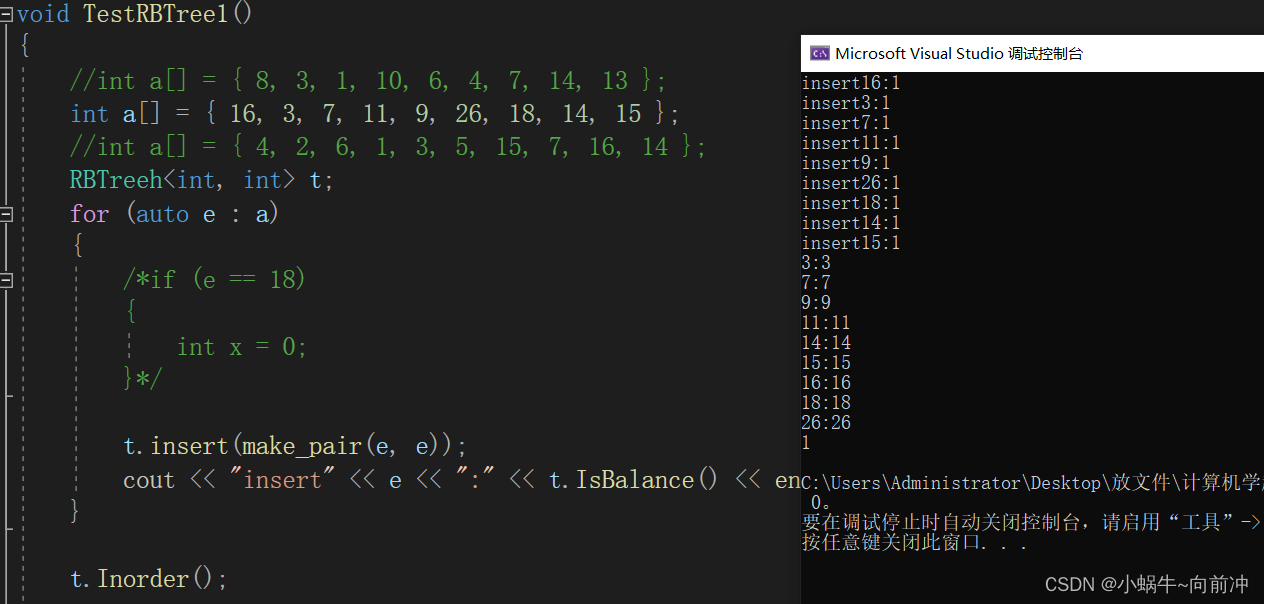
void TestRBTree1()
{//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTreeh<int, int> t;for (auto e : a){/*if (e == 18){int x = 0;}*/t.insert(make_pair(e, e));cout << "insert" << e << ":" << t.IsBalance() << endl;}t.Inorder();cout << t.IsBalance() << endl;
}void TestRBTree2()
{srand(time(0));const size_t N = 100000;RBTreeh<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand();t.insert(make_pair(x, x));//cout << t.IsBalance() << endl;}//t.Inorder();cout << t.IsBalance() << endl;
}
3、完整代码实现
#pragma onceenum Colour
{RED,BLACK,
};template<class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}
};template<class K,class V>
class RBTreeh
{typedef RBTreeNode<K,V> Node;
public:bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//找到插入位置Node* parent = nullptr;Node* cur = _root;while (cur){//到左子树找if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}//找到了cur = new Node(kv);cur->_col = RED;//默认颜色为红色//链接节点if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//插入后要调整红黑树//如果父亲存在且为红色while (parent && parent->_col == RED){Node* grandparent = parent->_parent;//情况1:cur为红色,p和u都为红色,g为黑色,这里的u是存在的//解决方法:p和n都变黑,g变红,在把cur当做g继续调整if (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;//更新parentparent = cur->_parent;}else//情况2+3 uncle存在且为黑色或者uncle不存在{if (cur == parent->_left){//情况2//解决方法:右单旋,将p变黑,g变红RotateR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}else//情况3:双旋转{RotateL(parent);RotateR(grandparent);grandparent->_col = RED;cur->_col = BLACK;//双旋转后cur变为了根}//这里类比根节点为色,不需要在调整了break;}}else//grandparent->right == parent{//这里也是和上面一样分为三种情况Node* grandparent = parent->_parent;Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;//更新parentparent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandparent);//左单旋转parent->_col = BLACK;grandparent->_col = RED;}else{RotateR(parent);RotateL(grandparent);grandparent->_col = RED;cur->_col = BLACK;//双旋转后cur变为了根}break;}}}//调整完成,把根节点变黑_root->_col = BLACK;return true;}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* grandparent = parent->_parent;//让subLR变为parent的左,parent->_left = subLR;//这里要判断一下subLR不为空if (subLR){subLR->_parent = parent;}//parent变为subL的右subL->_right = parent;parent->_parent = subL;//parent就是为根if (grandparent == nullptr){_root = subL;subL->_parent = grandparent;}else{//parnet是上grandparent的左子树if (grandparent->_left == parent){grandparent->_left = subL;}else{grandparent->_right = subL;}subL->_parent = grandparent;}}//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;Node* ppNode = parent->_parent;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;//parnet为根,要更新根if (ppNode == nullptr){_root = subR;subR->_parent = ppNode;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void Inorder(){_Inorder(_root);}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}bool Check(Node* root, int blackNum, const int ref){if (root == nullptr){//已经递归到最深处进行,本路径的黑节点树和ref数量对比if (blackNum != ref){cout << "违反规则:本条路径的黑色节点的数量跟最左路径不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则:出现连续红色节点" << endl;return false;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);}bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}//求出最左路节点有多少个黑节点int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK){++ref;}left = left->_left;}return Check(_root, 0, ref);}
private:Node* _root = nullptr;};void TestRBTree1()
{//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTreeh<int, int> t;for (auto e : a){/*if (e == 18){int x = 0;}*/t.insert(make_pair(e, e));cout << "insert" << e << ":" << t.IsBalance() << endl;}t.Inorder();cout << t.IsBalance() << endl;
}//void TestRBTree2()
//{
// srand(time(0));
// const size_t N = 100000;
// RBTreeh<int, int> t;
// for (size_t i = 0; i < N; ++i)
// {
// size_t x = rand();
// t.insert(make_pair(x, x));
// //cout << t.IsBalance() << endl;
// }
//
// //t.Inorder();
// cout << t.IsBalance() << endl;
//}四、AVL树和红黑树的比较
AVL树(Adelson-Velsky and Landis tree)和红黑树都是自平衡的二叉搜索树,它们在维持树的平衡性上采用了不同的策略。以下是它们之间的一些比较:
平衡性维护策略:
- AVL树: 通过保持任意节点的左右子树的高度差(平衡因子)不超过1来维护平衡。在每次插入或删除操作后,可能需要旋转来恢复平衡。
- 红黑树: 通过引入额外的颜色信息和一些规则,确保树的高度保持在较小的范围内。具体来说,红黑树的平衡性维护是通过节点的颜色和一些颜色约束来实现的。
平衡因子和颜色信息:
- AVL树: 使用平衡因子(Balance Factor)来表示每个节点左右子树的高度差。通常,平衡因子为 -1、0、1。
- 红黑树: 使用颜色信息(红色或黑色)来表示树的平衡状态。通过遵循红黑树的性质,确保了树的平衡。
旋转操作:
- AVL树: 插入或删除可能需要执行多次旋转操作,包括左旋、右旋、左右旋、右左旋等。
- 红黑树: 插入或删除通常只需要执行一到两次旋转操作,因为红黑树引入了颜色信息,更灵活地维持平衡。
性能影响:
- AVL树: 由于 AVL 树对平衡的要求更为严格,因此在插入和删除等操作时可能会导致更多的旋转,相对来说更耗费性能。
- 红黑树: 由于其相对宽松的平衡条件,红黑树在插入和删除等操作时通常执行的旋转较少,因此性能可能相对更好。
应用场景:
- AVL树: 适用于对搜索性能有较高要求的场景,例如在数据库中需要快速检索数据。
- 红黑树: 通常在需要高效的插入和删除操作的情况下使用,例如在集合类的实现中。
总体而言,选择 AVL 树还是红黑树取决于应用的特定需求。如果搜索操作远远超过插入和删除,可能更倾向于使用 AVL 树。而在插入和删除操作频繁的情况下,红黑树可能更为适用。
相关文章:

[数据结构]-红黑树
前言 作者:小蜗牛向前冲 名言:我可以接受失败,但我不能接受放弃 如果觉的博主的文章还不错的话,还请点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正 目录 一、红黑树的…...

Android 13.0 Launcher3 app列表页桌面图标按安装时间排序
1.概述 在13.0的系统rom定制化开发中,在对Launcher3进行功能开发时,系统默认的app列表页排序是安装app名称进行排序的, 由于功能的需要要求按照app安装时间进行排序,这就需要找到相关的排序地方,进行排序方式的修改就能完成这个功能 2.Launcher3 app列表页桌面图标按安装…...

QFont如何设置斜体|QlineEdit设置只能输入数字|QThread::finished信号发出后worker未调用析构函数
QFont如何设置斜体 要设置 QFont 的斜体,你可以使用 setItalic() 方法。以下是一个示例代码: #include <QApplication> #include <QLabel> #include <QFont> int main(int argc, char *argv...

中伟视界:创新解决方案,搭建自适应的AI算法模型训练平台
搭建AI算法模型自训练平台是当今人工智能领域的热门话题,但是其中存在着许多技术难点需要克服。 自训练平台需要具备高效的算法模型,这就要求能够处理庞大的数据量并进行高速计算。 平台需要具备强大的数据管理及存储能力,以满足训练过程中的…...
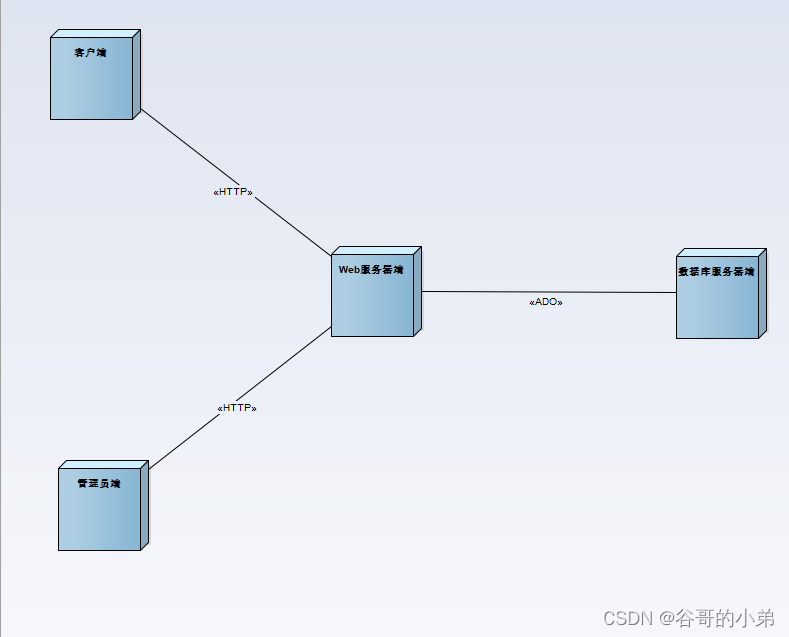
UML建模图文详解教程08——部署图
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl本文参考资料:《UML面向对象分析、建模与设计(第2版)》吕云翔,赵天宇 著 部署图概述 部署图(deployment diagram)也被译作配置…...
发布鸿蒙的第一个java应用
1.下载和安装华为自己的app开发软件DevEco Studio HUAWEI DevEco Studio和SDK下载和升级 | HarmonyOS开发者 2.打开IDE新建工程(当前用的IDEA 3.1.1 Release) 选择第一个,其他的默认只能用(API9)版本,搞了半天才发现8ÿ…...
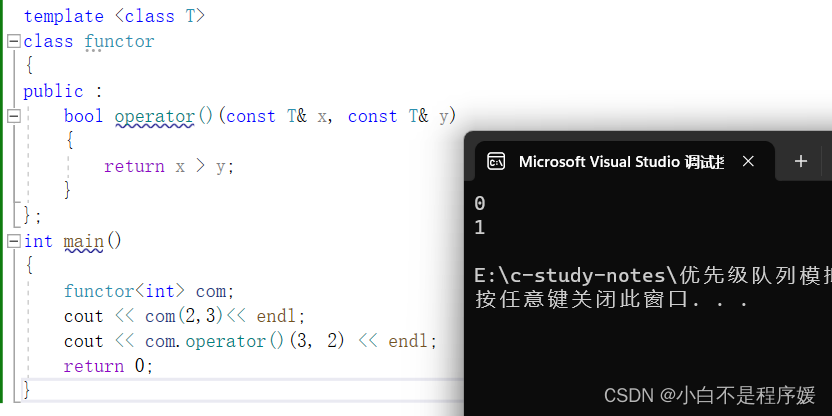
【C++干货铺】优先队列 | 仿函数
个人主页点击直达:小白不是程序媛 C系列专栏:C干货铺 代码仓库:Gitee 目录 优先队列(priority_queue )的介绍和使用 priority_queue的介绍 priority_queue的使用 大堆 小堆 priority_queue的模拟实现 仿…...

突破技术障碍:软件工程师如何应对项目中的难题?
在软件开发项目中,工程师常常会遇到各种技术难题。这些难题可能涉及到复杂的算法、不兼容的系统、难以预见的软件行为,或者其他许多方面。 以下是一些策略和方法,可以帮助软件工程师有效地应对这些挑战: 1、理解问题:…...

Linux(7):Vim 程序编辑器
vi 基本上 vi 共分为三种模式,分别是【一般指令模式】、【编辑模式】与【指令列命令模式】。 这三种模式的作用分别是: 一般指令模式(command mode) 以 vi 打开一个文件就直接进入一般指令模式了(这是默认的模式,也简称为一般模式)。在这个模…...

windows搭建gitlab教程
1.安装gitlab 说明:由于公司都是windows服务器,这里安装以windows为例,先安装一个虚拟机,然后安装一个docker(前提条件) 1.1搜索镜像 docker search gitlab #搜索所有的docker search gitlab-ce-zh #搜索…...

力扣:单调栈算法思路题
单调栈分为单调递增栈和单调递减栈,通过使用单调栈我们可以访问到最近一个比它大(小)的元素。 🍊 单调递增栈:单调递增栈就是从栈底到栈顶数据是依次递增,通常是寻找某方向第一个比它小的元素。 …...
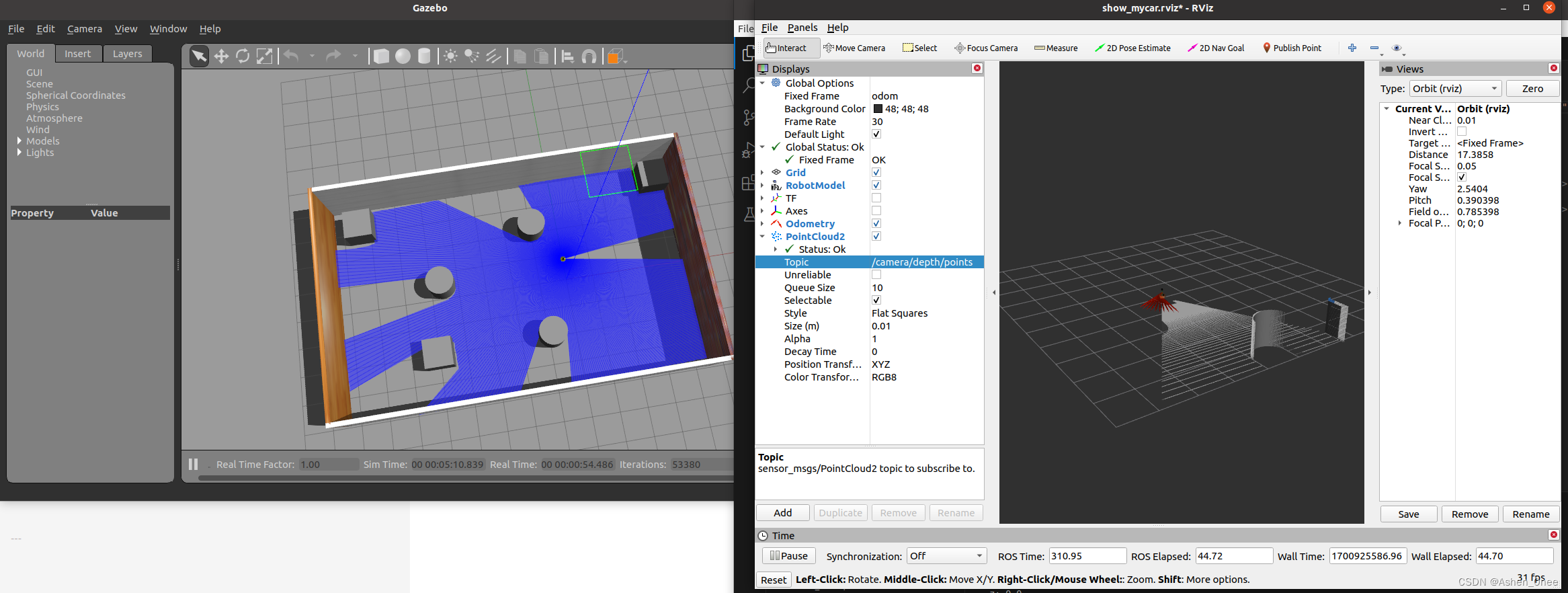
11 月 25 日 ROS 学习笔记——3D 建模与仿真
文章目录 前言一、在 ROS 中自定义机器人的3D模型1. 在 rviz 里查看3D模型2. xacro 二、Gazebo1. urdf 集成 gazebo2. 综合应用1). 运动控制及里程计2). 雷达仿真3). 摄像头信息仿真4). kinect 深度相机仿真5). 点云 前言 本文为11 月 25 日 ROS 学习笔记——3D 建模与仿真&am…...
MidJourney笔记(3)-Prompts
MidJourney的Prompts介绍 MidJourney的Prompts是MidJourney的核心之一,这也是我们后续使用MidJourney过程中最重要的工作内容,根据生成的图片,不断的优化我们的Prompts内容。 那Prompts的中文意思是提示的意思。 Prompts的提示语有很多,最基础的用法就是: /imagine prompt…...

贪心 D. Least Cost Bracket Sequence
Problem - D - Codeforces 题目大意:给一个只包含(,),?三个字符的字符串。每个?可以转为(或者),对于第 i i i个?转为(需要花费 a i a_i ai,转为)需要花费 b i b_i bi。现在问能否让该字符串转为合法的括号匹配…...
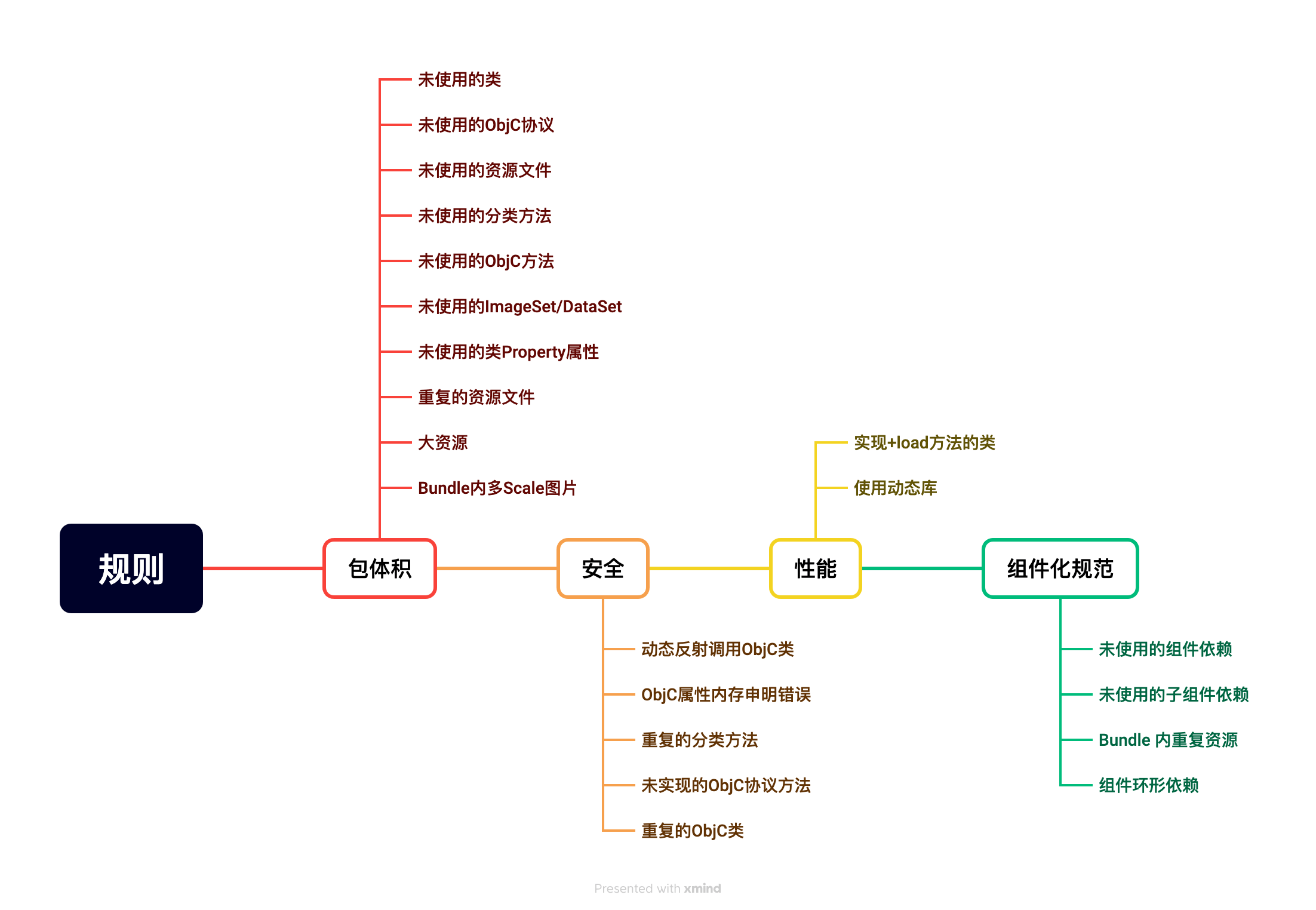
iOS APP包分析工具 | 京东云技术团队
介绍 分享一款用于分析iOSipa包的脚本工具,使用此工具可以自动扫描发现可修复的包体积问题,同时可以生成包体积数据用于查看。这块工具我们团队内部已经使用很长一段时间,希望可以帮助到更多的开发同学更加效率的优化包体积问题。 工具下载…...
在 VSCode 中使用 GDB 进行 C/C++ 程序调试(图文版)
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,数据结构,Linux基础,ARM开发板,网络编程等领域UP🌍快上🚘,一起学习,让我们成为一个强大的攻城狮࿰…...

任意文件读取漏洞理解
任意文件读取漏洞理解 1. 漏洞描述: 任意文件读取漏洞是指攻击者可以利用漏洞读取系统上的任意文件,包括敏感信息的配置文件、用户数据甚至系统文件,从而获取未经授权的访问权限。 2. 漏洞原理: 这种漏洞通常是由程序处理用户输入…...

linux 安装yum
问题1:File "/usr/libexec/urlgrabber-ext-down", line 28 except OSError, e: ^ 问题2:yum File "/usr/bin/yum", line 30 except KeyboardInterrupt, e: ^ vim /usr/…...

数学启发式
学习资料: 优化求解器 | Gurobi 数学启发式算法:参数类型与案例实现 数学启发式算法 | 可行性泵 (Feasibility Pump)算法精讲:一份让您满意的【理论介绍编程实现数值实验】学习笔记(PythonGurobi实现) 大佬到底是大佬!这些资料太…...

Win10/Win11 使用Wsl的Ubuntu 子系统搭建CGO环境,相当于Ubuntu下开发。GO环境CGO搭建,支持交叉编译
背景: 之前是使用Mac 开发,最近切换到win11下面。发现使用cgo编译有问题。 下面记载了我的使用方法。 环境: win11(win10理论一样) win11 安装了wsl2的环境,并且安装了ubuntu系统。 在win11 上面安装了g…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...

C++ 类基础:封装、继承、多态与多线程模板实现
前言 C 是一门强大的面向对象编程语言,而类(Class)作为其核心特性之一,是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性,包括封装、继承和多态,同时讨论类中的权限控制,并展示如何使用类…...
