【C++干货铺】优先队列 | 仿函数
=========================================================================
个人主页点击直达:小白不是程序媛
C++系列专栏:C++干货铺
代码仓库:Gitee
=========================================================================
目录
优先队列(priority_queue )的介绍和使用
priority_queue的介绍
priority_queue的使用
大堆
小堆
priority_queue的模拟实现
仿函数的介绍和使用
仿函数的介绍
仿函数的使用
优先队列(priority_queue )的介绍和使用
priority_queue的介绍
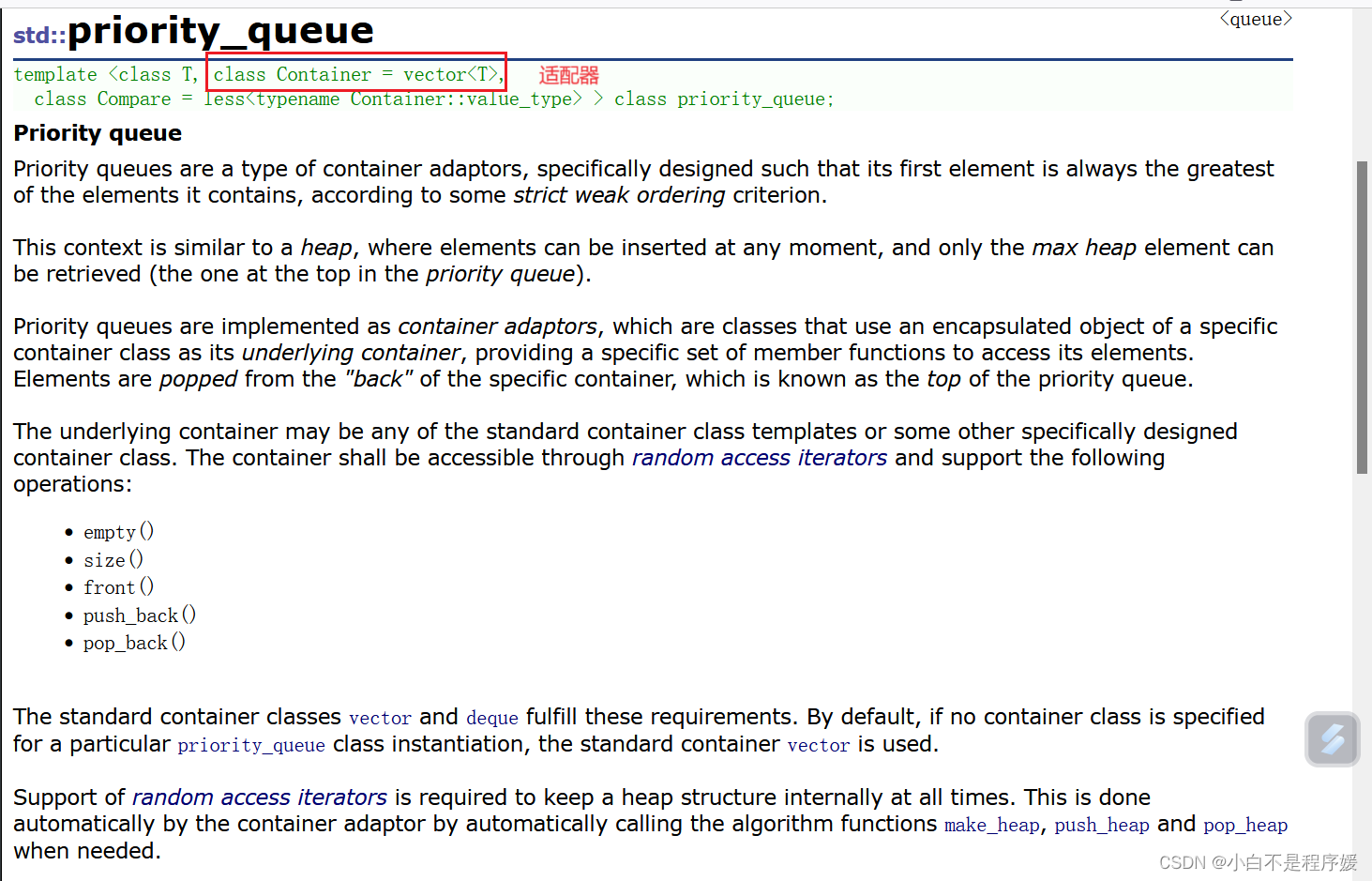
1. 优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。
2. 此上下文类似于堆,在堆中可以随时插入元素,并且只能检索最大堆元素(优先队列中位于顶部的元素)。
3. 优先队列被实现为容器适配器,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特定的成员函数来访问其元素。元素从特定容器的“尾部”弹出,其称为优先队列的顶部。
4. 底层容器可以是任何标准容器类模板,也可以是其他特定设计的容器类。容器应该可以通过随机访问迭代器访问,并支持以下操作:
- empty():检测容器是否为空
- size():返回容器中有效元素个数
- front():返回容器中第一个元素的引用
- push_back():在容器尾部插入元素
- pop_back():删除容器尾部元素
5. 标准容器类vector和deque满足这些需求。默认情况下,如果没有为特定的priority_queue类实例化指定容器类,则使用vector。
6. 需要支持随机访问迭代器,以便始终在内部保持堆结构。容器适配器通过在需要时自动调用算法函数make_heap、push_heap和pop_heap来自动完成此操作
priority_queue的使用
优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。
注意:
默认情况下priority_queue是大堆。
| 函数名称 | 函数作用 |
| priority_queue() | 构造一个空的优先级队列 |
| empty( ) | 检测优先级队列是否为空,是返回true,否则返回 false |
| top( ) | 返回优先级队列中最大(最小元素),即堆顶元素 |
| push(x) | 在优先级队列中插入元素x |
| pop() | 删除优先级队列中最大(最小)元素,即堆顶元素 |
大堆
priority_queue<int,vector<int>> q1;q1.push(5);q1.push(23);q1.push(45);q1.push(7);q1.push(9);q1.push(2);q1.push(53);q1.push(34);cout << q1.size() << endl;while (!q1.empty()){cout << q1.top() << " ";q1.pop();}
小堆
priority_queue<int,vector<int>,greater<int>> q1;q1.push(5);q1.push(23);q1.push(45);q1.push(7);q1.push(9);q1.push(2);q1.push(53);q1.push(34);cout << q1.size() << endl;while (!q1.empty()){cout << q1.top() << " ";q1.pop();} 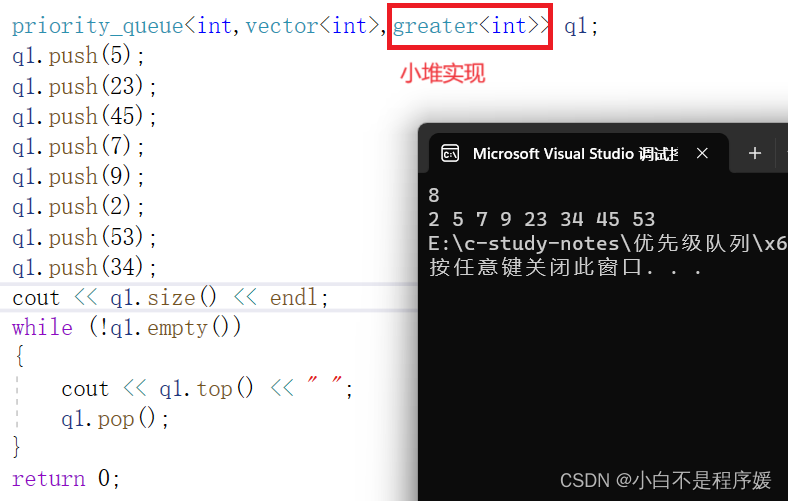
priority_queue的模拟实现
通过对priority_queue的底层结构就是堆,因此此处只需对对进行通用的封装即可。
template <class T, class Container=vector<T>>class priority_queue{public:void adjust_up(int child){int parent = (child - 1) / 2;while (child > 0){if (_con[parent] < _con[child]){swap(_con[parent], _con[child]);child = parent;parent = (child - 1) / 2;}else{break;}}}void push(const T& x){_con.push_back(x);adjust_up(_con.size() - 1);}void adjust_down(int parent)//{size_t child = parent * 2 + 1;//while (child < _con.size()){if (child + 1 < _con.size() &&_con[child] < _con[child + 1]){++child;}if(_con[parent] < _con[child]){swap(_con[parent], _con[child]);parent = child;child = parent * 2 +1 ;}else{break;}}}void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();adjust_down(0);}const T& top(){return _con[0];}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};但是我们编写完成后发现,只能实现大堆/小堆的一种;实现另一种时候需要自己改变函数中的符号,比较麻烦;在C语言中我们会使用函数指针,回调函数解决此问题;但是函数指针比较难以理解和使用,C++就出现了仿函数。
仿函数的介绍和使用
仿函数的介绍
仿函数(functor),就是使一个类的使用看上去像一个函数。其实现就是类中实现一个operator(),这个类就有了类似函数的行为,就是一个仿函数类了。
有些时候,我们在写代码时会发现,某些功能实现的代码会不断的在不同的成员函数中用到,可又不好将这些代码独立出来成为类的一个成员函数,但又很想复用这些代码。写一个公共的函数是一个解决方法,不过函数用到的一些变量,就可能成为公共的全局变量。而且为了复用这么一片代码,就要单立出一个函数,也不好维护,这时就可以用仿函数了。写一个简单类,除了那些维护一个类的函数成员外,就只是实现一个operator(),在类实例化时,就将要用的,非参数的元素传入类中。这样就免去了对一些公共变量全局化的维护。同时,又可以使那些代码独立出来,以便下次复用。而且,这些仿函数还可以用关联、聚合、依赖的类之间的关系,与用到他们的类组合在一起,这样有利于资源的管理(这点可能是它相对于函数最显著的优点了)。如果再配合上模板技术和policy编程思想,就更是威力无穷了,大家可以慢慢的体会。
仿函数的使用
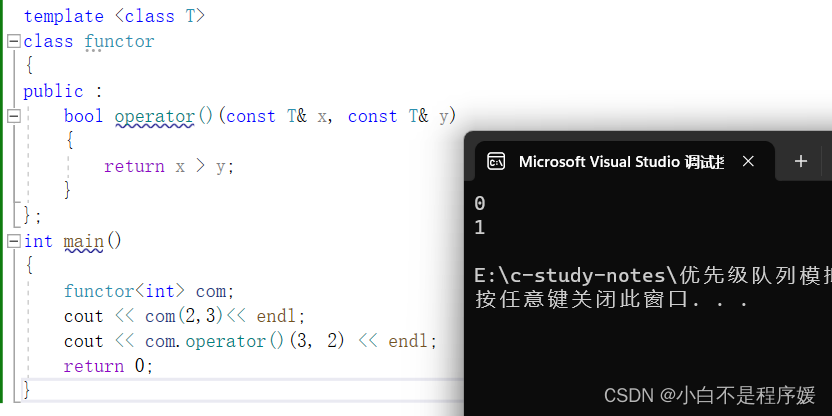
template <class T>
class functor
{
public :bool operator()(const T& x, const T& y){return x > y;}
};
int main()
{functor<int> com;cout << com(2,3)<< endl;cout << com.operator()(3, 2) << endl;return 0;
}
根据仿函数的功能和特性我们可以配合priority_queue的模板,模拟实现和STL库中的priority_queue。只需要在模板中加入一个比较器,默认缺省为实现大堆,在实例化时候可以选择大小堆这样就可以不用直接修改符号了。
template <class T, class Container=vector<T>,class Compare=Less<T>>class priority_queue{public:void adjust_up(int child)//{Compare com;int parent = (child - 1) / 2;//while (child > 0){if (com(_con[parent] , _con[child])){swap(_con[parent], _con[child]);child = parent;parent = (child - 1) / 2;}else{break;}}}void push(const T& x){_con.push_back(x);adjust_up(_con.size() - 1);}void adjust_down(int parent)//{Compare com;size_t child = parent * 2 + 1;//while (child < _con.size()){if (child + 1 < _con.size() && com(_con[child], _con[child + 1])){++child;}if(com (_con[parent] , _con[child])){swap(_con[parent], _con[child]);parent = child;child = parent * 2 +1 ;}else{break;}}}void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();adjust_down(0);}const T& top(){return _con[0];}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};//大堆
template <class T>
class Less
{
public:bool operator()(const T& x, const T& y){return x < y;}
};
//小堆
template <class T>
class Greater
{
public:bool operator()(const T& x, const T& y){return x > y;}
};今天对C++中priority_queue和仿函数的介绍、使用、模拟实现的分享到这就结束了,希望大家读完后有很大的收获,也可以在评论区点评文章中的内容和分享自己的看法。您三连的支持就是我前进的动力,感谢大家的支持!! !
相关文章:

【C++干货铺】优先队列 | 仿函数
个人主页点击直达:小白不是程序媛 C系列专栏:C干货铺 代码仓库:Gitee 目录 优先队列(priority_queue )的介绍和使用 priority_queue的介绍 priority_queue的使用 大堆 小堆 priority_queue的模拟实现 仿…...

突破技术障碍:软件工程师如何应对项目中的难题?
在软件开发项目中,工程师常常会遇到各种技术难题。这些难题可能涉及到复杂的算法、不兼容的系统、难以预见的软件行为,或者其他许多方面。 以下是一些策略和方法,可以帮助软件工程师有效地应对这些挑战: 1、理解问题:…...

Linux(7):Vim 程序编辑器
vi 基本上 vi 共分为三种模式,分别是【一般指令模式】、【编辑模式】与【指令列命令模式】。 这三种模式的作用分别是: 一般指令模式(command mode) 以 vi 打开一个文件就直接进入一般指令模式了(这是默认的模式,也简称为一般模式)。在这个模…...

windows搭建gitlab教程
1.安装gitlab 说明:由于公司都是windows服务器,这里安装以windows为例,先安装一个虚拟机,然后安装一个docker(前提条件) 1.1搜索镜像 docker search gitlab #搜索所有的docker search gitlab-ce-zh #搜索…...

力扣:单调栈算法思路题
单调栈分为单调递增栈和单调递减栈,通过使用单调栈我们可以访问到最近一个比它大(小)的元素。 🍊 单调递增栈:单调递增栈就是从栈底到栈顶数据是依次递增,通常是寻找某方向第一个比它小的元素。 …...
11 月 25 日 ROS 学习笔记——3D 建模与仿真
文章目录 前言一、在 ROS 中自定义机器人的3D模型1. 在 rviz 里查看3D模型2. xacro 二、Gazebo1. urdf 集成 gazebo2. 综合应用1). 运动控制及里程计2). 雷达仿真3). 摄像头信息仿真4). kinect 深度相机仿真5). 点云 前言 本文为11 月 25 日 ROS 学习笔记——3D 建模与仿真&am…...
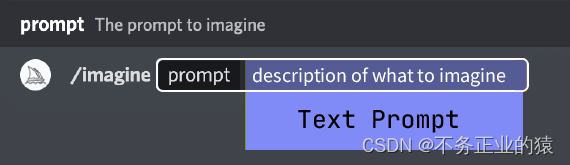
MidJourney笔记(3)-Prompts
MidJourney的Prompts介绍 MidJourney的Prompts是MidJourney的核心之一,这也是我们后续使用MidJourney过程中最重要的工作内容,根据生成的图片,不断的优化我们的Prompts内容。 那Prompts的中文意思是提示的意思。 Prompts的提示语有很多,最基础的用法就是: /imagine prompt…...

贪心 D. Least Cost Bracket Sequence
Problem - D - Codeforces 题目大意:给一个只包含(,),?三个字符的字符串。每个?可以转为(或者),对于第 i i i个?转为(需要花费 a i a_i ai,转为)需要花费 b i b_i bi。现在问能否让该字符串转为合法的括号匹配…...
iOS APP包分析工具 | 京东云技术团队
介绍 分享一款用于分析iOSipa包的脚本工具,使用此工具可以自动扫描发现可修复的包体积问题,同时可以生成包体积数据用于查看。这块工具我们团队内部已经使用很长一段时间,希望可以帮助到更多的开发同学更加效率的优化包体积问题。 工具下载…...
在 VSCode 中使用 GDB 进行 C/C++ 程序调试(图文版)
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,数据结构,Linux基础,ARM开发板,网络编程等领域UP🌍快上🚘,一起学习,让我们成为一个强大的攻城狮࿰…...

任意文件读取漏洞理解
任意文件读取漏洞理解 1. 漏洞描述: 任意文件读取漏洞是指攻击者可以利用漏洞读取系统上的任意文件,包括敏感信息的配置文件、用户数据甚至系统文件,从而获取未经授权的访问权限。 2. 漏洞原理: 这种漏洞通常是由程序处理用户输入…...

linux 安装yum
问题1:File "/usr/libexec/urlgrabber-ext-down", line 28 except OSError, e: ^ 问题2:yum File "/usr/bin/yum", line 30 except KeyboardInterrupt, e: ^ vim /usr/…...

数学启发式
学习资料: 优化求解器 | Gurobi 数学启发式算法:参数类型与案例实现 数学启发式算法 | 可行性泵 (Feasibility Pump)算法精讲:一份让您满意的【理论介绍编程实现数值实验】学习笔记(PythonGurobi实现) 大佬到底是大佬!这些资料太…...

Win10/Win11 使用Wsl的Ubuntu 子系统搭建CGO环境,相当于Ubuntu下开发。GO环境CGO搭建,支持交叉编译
背景: 之前是使用Mac 开发,最近切换到win11下面。发现使用cgo编译有问题。 下面记载了我的使用方法。 环境: win11(win10理论一样) win11 安装了wsl2的环境,并且安装了ubuntu系统。 在win11 上面安装了g…...

CSS新特性(2-2)
CSS新特性(2-2) 前言box相关box-shadow background背景rgba颜色与透明度transform:rotate(Xdeg) 2D旋转transform:tranlate 平移 前言 本文继续讲解CSS3其他的新特性,想看之前新特性点击这里,那么好本文正式开始。 box相关 box…...
为什么,word文件在只读模式下,仍然能编辑?
Word文档设置了只读模式,是可以编辑的,但是当我们进行保存的时候就会发现,word提示需要重命名并选择新路径才能够保存。 这种操作,即使可以编辑文字,但是原文件是不会受到影响的,编辑之后的word文件会保存到…...

29 - 装饰器模式:如何优化电商系统中复杂的商品价格策略?
开始今天的学习之前,我想先请你思考一个问题。假设现在有这样一个需求,让你设计一个装修功能,用户可以动态选择不同的装修功能来装饰自己的房子。例如,水电装修、天花板以及粉刷墙等属于基本功能,而设计窗帘装饰窗户、…...
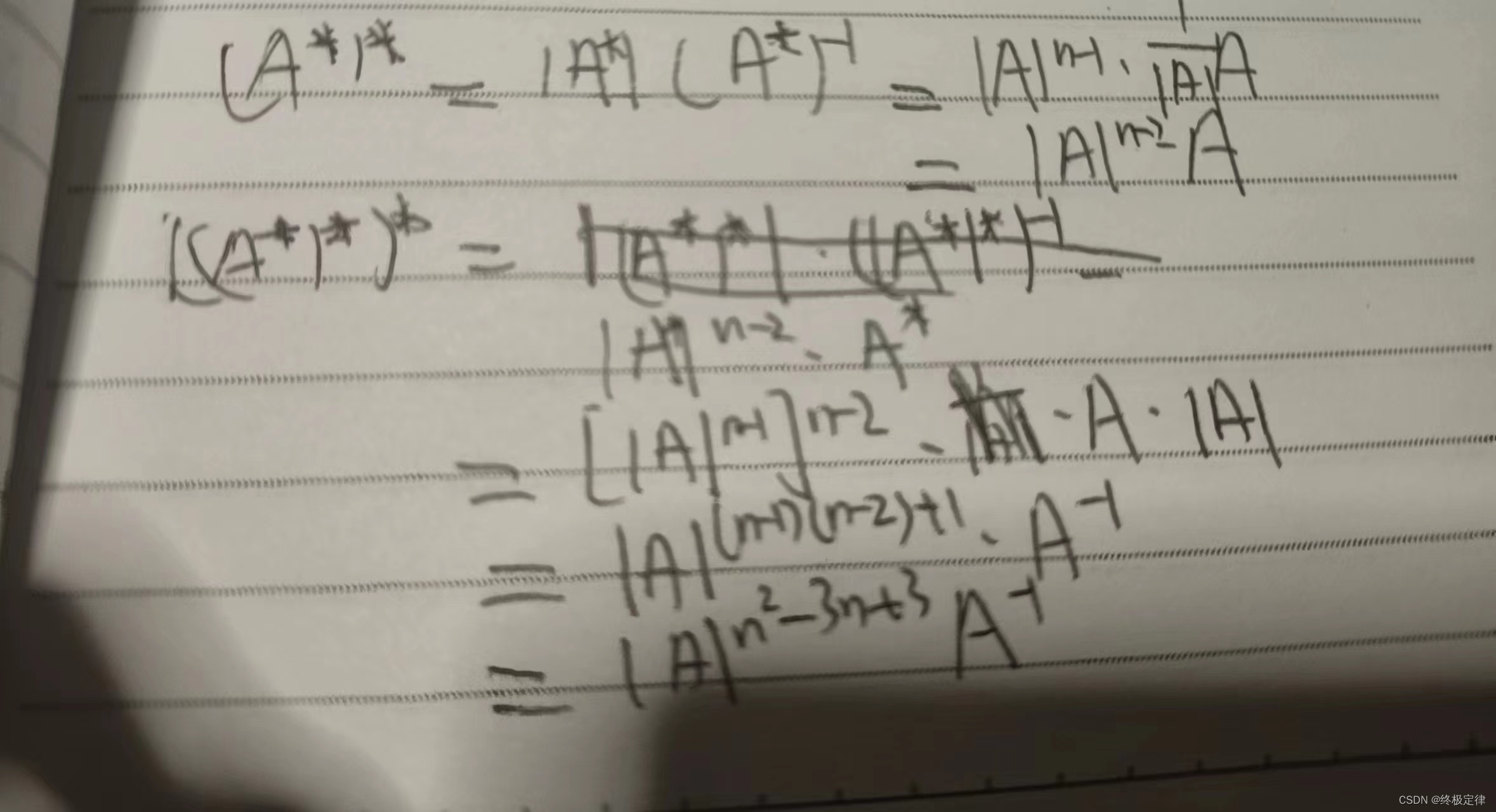
逆矩阵相关性质与例题
1.方阵的行列式:就是将方阵中的每一个元素转换至行列式中。 1.性质一:转置方阵的行列式等于转置前的行列式。(对标性质:行列式与它的转置行列式相等) 2.性质二:|ka||a|*k的n次方,n为方阵阶数。 …...

Ruoyi项目传List到后台并使用Excel模板下载数据的方法以及遇到的各种前后端数据交互问题
import { download } from @/utils/requestconst app = createApp(App)// 全局方法挂载 app.config.globalProperties.download = download 首先因为ruoyi-ui中的main.js有配置如上全局注册: 因此只需要在vue中定义一个方法直接使用this.download调用下载即可: (download的3…...

区块链技术将如何影响未来的数字营销?
你是否听腻了区块链和数字营销等流行语,却不明白它们对未来意味着什么?那么,准备好系好安全带吧,因为区块链技术将彻底改变我们对数字营销的看法。从建立消费者信任到提高透明度和效率,其可能性是无限的。 让我们来探…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
